Attitude Estimation Based on Conjugate Gradient and Complementary Filter*

SUN Jinqiu，YOU Youpeng，FU Zhongyun

(1.College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China; 2.Nanhang Jincheng College，Nanjing 211156，China)

Attitude Estimation Based on Conjugate Gradient and Complementary Filter*

SUN Jinqiu1，2*，YOU Youpeng1，FU Zhongyun2

(1.College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China; 2.Nanhang Jincheng College，Nanjing 211156，China)

In order to improve the precision of attitude estimation，a novel attitude estimation algorithm based on conjugate gradient and complementary filter is proposed.The quaternion representation used in the proposed system for attitude estimation，is optimized based on conjugate gradient algorithm with magnetometer and accelerometer data，and then fused with the updated quaternion from gyroscope data based on complementary filter.Finally，experiment results verify that the proposed algorithm based on conjugate gradient and complementary filter improves the static and dynamic properties of attitude estimation system，and has better performance than the Kalman filter and gradient descent filter especially when the attitude has drastic changes.

sensor;attitude estimation;conjugate gradient;complementary filter;quaternion

为提高捷联惯导系统的姿态解算精度，人们开展了大量的研究工作:一方面寻找更合适的姿态解算方法，另一方面对多种传感器的测量值进行数据融合。

常见的姿态解算方法有:欧拉角法、方向余弦法、四元数法、等效旋转矢量法、对偶四元数法。欧拉角法直观，容易理解，但存在三角函数计算问题和方程奇异现象。方向余弦法避免了欧拉角法的方程奇异问题，但要求解九个微分方程，计算量大。四元数法只需要求解四个微分方程，计算量小，实际中多被采用，但存在有限转动引起不可交换性误差的问题。等效旋转矢量法弥补了四元数的不足，但计算量有所增加［1］。对偶四元数法是描述一般性刚体运动最简洁、最有效的数学工具。但其技术还需要进一步完善［2］。

捷联惯导系统中，通常采用多种传感器组成组合导航系统，所以要选择一个最优的在线数据融合策略，将多种传感器的数据进行融合。常用的数据融合算法有:扩展卡尔曼滤波EKF(Extended Kalman Filter)，无迹卡尔曼滤波UKF(Unscented Kalman Filter)，梯度下降法，容积卡尔曼滤波CKF(Cubature Kalman Filter)，粒子滤波PF(Particle Filter)，互补滤波CF(Complementary Filter)等。EKF是应用最广泛的有一种非线性系统的滤波方法，但其存在线性化误差、截断误差及发散问题［3－7］。朱丰超［8］、Lin Zhao［9］、Yue Pan［10］等人将UKF应于姿态检测中，实验结果表明，其收敛速度、估计精度、稳定性都要高于EKF。Tang Xiaojun［11］将CKF应在航天器的姿态估计中，CKF估计精度又要高于UKF，但计算量有所增加。互补滤波是从频率分辨和消除噪声，原理简单，计算量最小的一种滤波方式，但其高、低通滤波器转接频率难以确定。文献［12］中将梯度下降法应用于姿态解算，性能优于卡尔曼滤波。该方法具有计算量少，对初始点要求低的优点，但与牛顿法和共轭梯度法相比，收敛较慢。

本文提出一种共轭梯度优化方法与互补滤波相结合的数据融合策略，共轭梯度法既克服了梯度下降法收敛慢的不足，又可避免牛顿法计算量大的缺点。其中，姿态解算采用四元数法;利用加速度计和磁强计的输出数据，通过共轭梯度方法对姿态四元数进行寻优估计，再将其和利用陀螺仪输出数据更新的四元数进行互补滤波，最终解算出欧拉角。

1 基于四元数法的姿态解算

1.1 姿态的坐标描述

通常将陀螺仪、磁强计和加速度计的测量数据定义到一个坐标系，称为载体坐标系b。与之相对应的绝对坐标系称为导航坐标系n(本文选用北、东、地的地理坐标系)。载体坐标系和导航坐标系之间的夹角就是描述载体航向的姿态角。γ、θ和ψ分别为载体的横滚角、俯仰角和航向角，如图1所示［1］。

图1 载体坐标系和导航坐标系以及欧拉角

1.2 姿态的四元数解算法

导航系统中，载体坐标系相对于导航坐标系的转动则可以运用转动四元数来表示:

四元数微分方程:

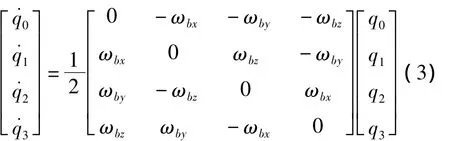
2 多传感器的数据融合

陀螺仪在工作时易受到载体震动的干扰而影响测量精度，并在积分过程中产生较大的累积误差。为获取更加准确的姿态，需要用加速度计和磁强计的测量数据对陀螺仪进行补偿。通常用加速度计数据去补偿俯仰角和横滚角，磁强计数据补偿航向角。但加速度计无法区分重力加速度和运动加速度，磁强计容易受到周围磁场的干扰，且这类误差是随机的，无法预先消除。因此本文先用加速度计和磁强计所测的数据，采用共轭梯度法对姿态四元数进行寻优处理。

2.1 基于共轭梯度法的四元数最优估计

加速度计和磁强计的三轴分别沿着载体坐标系以X，Y，Z的三轴方向安装，磁强计在载体坐标系三轴上的分量分别为mbx，mby，mbz，加速度计在载体坐标系三轴上的分量分别abx，aby，abz。理想情况下，重力场的参考方向为fg=［00g］T;地磁场的参考量为H=［Hn0Hd］］T。其中g是重力加速度，Hn和Hd分别是地磁场在北东地坐标系中北向分量和垂直分量。将fg和H补零，并单位化可得

理想的均匀重力场和地磁场的参考方向可通过载体导航坐标系下四元数转换到载体坐标系下，表示为:

其中Q*=q0－q1i－q2j－q3k，为Q的共轭四元数。

将式(6)和式(7)所得数据与加速度计与磁强计在载体坐标系下的测量数据相减便可得到测量误差。定义误差函数为:

则四元数的优化问题可转换为目标函数f(q)= e(q)Te(q)求最小值问题。

根据共轭梯度法，可按照式(9)更新载体姿态的四元数。

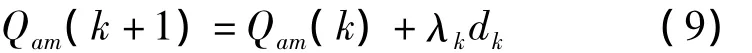
其中，λk为最优步长，dk为搜索方向。根据FR共轭梯度法，两者的计算如下［13］:

定义:▽f=JT(q)·e(q)

式中，JT(q)为e(q)的雅可比矩阵。

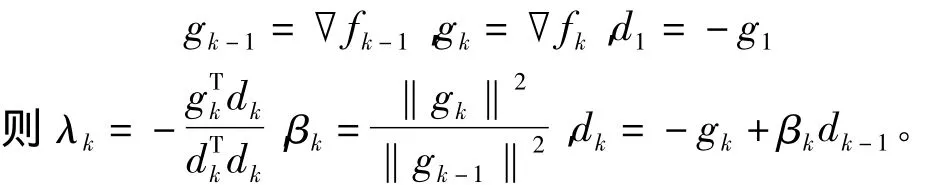
每次更新一个新的姿态后都需要迭代数次以得到最优解，实际应用中每次釆样只迭代一次也可以。为了跟下文的互补滤波相结合，本文每次采样只迭代一次。

2.2 互补滤波

陀螺仪短时间内可以提供高动态的姿态数据，但因漂移的影响，长时间后精度会降低。加速度计和磁强计测量误差不会随时间累计，但其短期内的精度差。利用两者在频域上的互补特性，采用互补滤波器对二者进行数据融合可提高姿态测量的精度。互补滤波的公式为:

其中，r为加权系数，取值为0～1之间，本文取经验值0.02;Qam(k+1)为通过共轭梯度法寻优得到的四元数;Qg(k+1)为由陀螺仪测量数据更新的四元数。

将式(4)、式(9)代入式(10)并简化，可得:

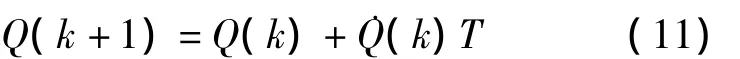
图2给出了本文姿态解算的全过程。利用陀螺仪输出数据，根据四元数微分方程得到˙Qg(k);将加速度计和磁强计的输出数据，与通过四元数估计值变换得到的相应数据相减，求差值e(k)，并建立误差函数f(q)，再利用共轭梯度法求解四元数更新的步长和梯度方向λkdk;最后根据互补滤波计算出Q(k+1)估计值。

图2 共轭梯度法和互补滤波相结合的原理图

3 实验测试与结果分析

3.1 测试平台

实验测试平台以STM32F103C8为CPU，传感器选用MPU－6050模块(整合了三轴加速度计和陀螺仪)，并通过I2C协议与CPU通讯。处理器完成姿态解算后，通过SPI将数据经2.4 GHz无线数据传输模块发送到上位机。上位机采用C#编写显示界面，可显示各传感器的测量数据和姿态欧拉角的数据和波形，并可将数据导到EXCELL中，进行进一步分析。系统的硬件结构和显示界面如图3所示。系统以100 Hz频率对传感器进行采样，可存储500个点的数据。因暂未采用磁强计，故只对俯仰角和横滚角进行了静态测试、水平滑动和动态测试。

图3 系统的硬件电路和显示界面

3.2 测试结果与分析

3.2.1 静态测试

将姿态测量单元置于水平台面上，理想的俯仰角应该为0°。当姿态检测单元处于静止时，单独使用加速度计时，如图4所示，输出的俯仰角信号带有一定的干扰噪声，最大误差为0.23°。单独使用陀螺仪，得到的俯仰角在5 s内角度值从9.0°累计到11.2°。使用本文所设计滤波方法，对陀螺仪和加速度计的数据进行融合后，静态误差可控制在0.023°以内。

图4 静态时俯仰角估计

图5 有运动加速度时俯仰角和横滚角的估计

3.2.2 水平滑动测试

加速计最大缺点是无法区分运动加速度和重力加速度，难以单独使用。本文将姿态测量单元放在水平桌面上，作快速滑动。理论上，俯仰角和横滚角均应该为0°。但直接由加速度计测量值经过解算，得到的俯仰角误差达到了22.3°，且运动加速度越大，该误差越大，如图5所示。经过本文设计的滤波器，将陀螺仪和加速度计的数据进行融合后，这个误差被减小到2°之内，横滚角误差在2.6°之内。可见，本文滤波方法对运动加速度有较好滤除作用。

3.2.3 动态测试

动态测试又分姿态变化较慢和姿态变化较快时两种情况。图6分别为姿态变换较慢时，采用卡尔曼滤波、梯度下降法以及本文滤波方法得到的估计值与AHRS(Attitude and Heading Reference System)得到的估计值对比效果。AHRS系统采用AHRS3000成品，该成品基于三轴陀螺仪、三轴加速度计和三轴磁力计，并采用自适应Kalman数据融合算法。

图7分别表示了对应于图6中各个滤波方法的估计误差。表1给出了各种滤波算法误差绝对值的均值、最大值和最小值。可得，本文所提出的滤波算法性能优于卡尔曼滤波和梯度下降法。

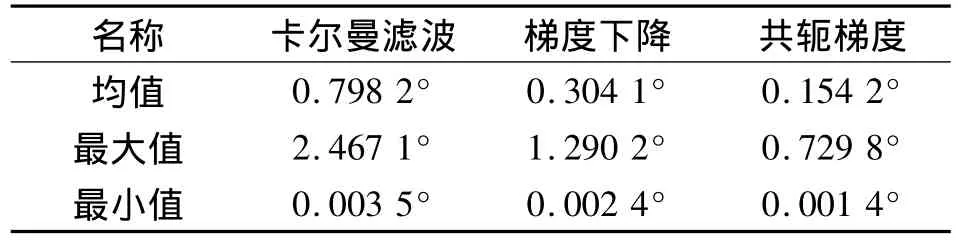
表1 姿态变换较慢时俯仰角估计误差表

为进一步验证本文滤波方法的有效性，还模拟了载体姿态变化较快时的情况。图8分别为采用卡尔曼滤波、梯度下降法和本文设计的共轭梯度法得到的俯仰角估计值和用加速度计得到实际测量值比较结果。可以看出，姿态剧烈变化的时候，卡尔曼滤波有明显的滞后，1 s左右才会跟踪上，且有稳态误差。梯度下降法有轻度滞后，200 ms跟踪上。本文设计的共轭梯度法几乎没有滞后，很好的跟踪了实际姿态的变化。说明了共轭梯度法比梯度下降法具有更快的收敛速度。

图6 姿态变化较慢时的俯仰角估计

图7 姿态变化较慢时的俯仰角估计误差

图8 姿态变化较快时的俯仰角估计

4 结论

本文提出了共轭梯度法和互补滤波相结合的方式，将多传感器的数据进行了融合，以提高姿态的解算精度。实验测试表明，这种融合策略，可以使姿态检测系统具有较好的静态特性和动态特性。尤其姿态变化剧烈的时候，本文提出的滤波方法性能明显优于卡尔曼滤波和梯度下降法滤波。如果提高一个解算周期内共轭梯度法的迭代次数，姿态的估计精度还可进一步提高，是后续研究的重点之一。

［1］丁军.基于微惯性传感器的姿态算法研究［D］.上海:上海交通大学，2013.

［2］李贵珍.基于对偶四元数的捷联惯导算法研究［D］.太原:中北大学，2012.

［3］叶锃锋，冯恩信.基于四元数和卡尔曼滤波的两轮车姿态稳定方法［J］.传感技术学报，2012，25(4):524－528.

［4］苑艳华，李四海，南江.基于卡尔曼滤波器的航姿系统测姿算法研究［J］.传感技术学报，2011，24(12):1723－1727.

［5］Jung Keun Lee，Edward J Park，Stephen N.Robinovitch.Estimation of Attitude and External Acceleration Using Inertial Sensor Measurement During Various Dynamic Conditions［J］.IEEE Transactions on Instrumentation and Measurement，2012，61(8):2262－2273.

［6］Ruan Xiaogang，Song Keke.An Adaptive Extended Kalman Filter for Attitude Estimation of Self-Balancing Two-Wheeled Robot［C］//International Conference on Electric Information and Control Enginee(ICEICE)，2011:4760－4763.

［7］Lou Lu，Xu Xin.An Approach to Improving Attitude Estimation U-sing Sensor Fusion for Robot Navigation［C］//Procedia Engineering，2011，15:5601－5605.

［8］朱丰超，姚敏立，贾维敏.基于低成本陀螺和倾角仪的姿态估计［J］.宇航学报，2011，32(8):1728－1732.

［9］Zhao Lin，Nie Qi，Guo Qiufen.Unscented Kalman Filtering for SINS Attitude Estimation［C］//IEEE International Conference on Control and Automation，2007:228－232.

［10］Pan Yue.Attitude Estimation of Miniature Unmanned Helicopter Using Unscented Kalman Filter［C］//International Conference on Transportation，Mechanical，and Electrical Engineering(TMEE).2011:1548－1551.

［11］Tang Xiaojun，Wei Jianli，Chen Kai.Square-Root Adaptive Cubature Kalman Filter with Application to Spacecraft Attitude Estimation［C］//International Conference on Information Fusion.2012: 1406－1412.

［12］Madgwick S.An Efficient Orientation Filter for Inertial and Inertial/Magnetic Sensor Arrays［R］.Report x-io and University of Bristol(UK)，2010.

［13］余刚.无约束优化问题共轭梯度法的研究［D］.北京:北京邮电大学，2007.

孙金秋(1979－)，女，博士生，讲师，主要从事机器人以及先进控制理论应用研究工作，523106551@qq.com;

游有鹏(1960－)，男，博导，教授，主要从事机电一体化控制，机器人以及数控技术等研究工作，youypeng@163.com。

基于共轭梯度法和互补滤波相结合的姿态解算算法*

孙金秋1，2*，游有鹏1，傅忠云2
(1.南京航空航天大学机电学院，南京210016;2.南京航空航天大学金城学院，南京211156)

为了提高姿态解算精度，提出了一种基于共轭梯度和互补滤波相结合的多传感器数据融合策略。系统采用四元数方法进行姿态解算。利用加速度计和磁强计的输出数据，通过共轭梯度方法对姿态四元数进行寻优估计，再将其和利用陀螺仪输出数据更新的四元数进行互补滤波，解算出姿态角。实验测试表明，这种融合策略使姿态检测系统静态性能和和动态性能均有所提高，尤其在姿态剧烈变化时，其性能明显优于卡尔曼滤波和梯度下降法。

传感器;姿态估计;共轭梯度法;互补滤波;四元数

TP391.9

A

1004－1699(2014)04－0524－05

2014－01－20修改日期:2014－04－04

C:6330

10.3969/j.issn.1004－1699.2014.04.019

项目来源:国家自然科学基金项目(51175263);基于9-SPS冗余并联机构的六维加速度传感器研究项目