负相依索赔条件下关于复合更新风险模型的精细大偏差

宋 立 新， 冯 敬 海， 袁 亮 亮*， 石 新 勇,2

( 1.大连理工大学 数学科学学院, 辽宁 大连 116024；2.中国人民解放军68048部队， 陕西 宝鸡 721013 )



应用数学

负相依索赔条件下关于复合更新风险模型的精细大偏差

宋 立 新1， 冯 敬 海1， 袁 亮 亮*1， 石 新 勇1,2

( 1.大连理工大学 数学科学学院, 辽宁 大连 116024；2.中国人民解放军68048部队， 陕西 宝鸡 721013 )

研究不独立、不同分布的精细大偏差问题，其中假设{Xn，n≥1}是一列负相依的随机变量序列，{Fn，n≥1}为其对应的分布函数列．在满足一定的条件下，重点解决非随机和的精细大偏差的下限问题，得到相对应的随机和的一致渐近结论，并将所得结论应用到更为实际的复合更新风险模型中，验证了其理论与实际价值．

精细大偏差；负相依；随机和；复合更新风险模型

0 引 言

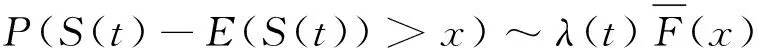
在精细大偏差的相关理论研究中，有较多的研究都只关注{Xn，n≥1}是独立同分布时的情形，经典的理论成果可见文献[1-4]．而目前，多数研究都聚集在变量间的相互关系以及相关重尾子族的扩张上，如文献[5-8]．文献[9]研究了独立不同分布情形下的随机变量和的精细大偏差．文献[10-11]研究了构造{N(t)，t≥0}的随机变量在相依情形下的精细大偏差．在这一过程中，陆续有人将精细大偏差的结论应用于普通的风险模型中，如文献[12]．而本文研究的则是负相依不同分布随机变量和的精细大偏差，并将其应用到改进后的复合更新风险模型中．

1 预备知识

1.1 两个重要的重尾子族

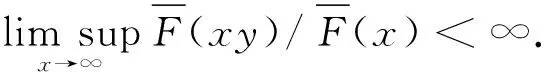
或等价地有

记

和

和

在文献[13]中，γF和μF分别称作F的上、下Matuszewska 指标．

1.2 负相依随机变量序列

定义1称随机变量序列{Xk，k≥1}

(1)下负象限相依(LND)，若对每一个n(n≥1)和所有的x1，…，xn，都有

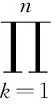
(1)

(2)上负象限相依(UND)，若对每一个n(n≥1)和所有的x1，…，xn，都有

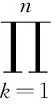
(2)

(3)负相依(ND)，若式(1)和式(2)对每一个n(n≥1)和所有的x1，…，xn同时成立．

当n=2时，LND、UND和ND等价．关于其对应的细节应用可见文献[5]．

下面给出LND(或UND)随机变量的几个性质，具体的推导过程可见文献[14]．

性质1对随机变量序列{Xk，k≥1}和实值函数{fk，k≥1}，

(1)若{Xk，k≥1}是LND(或UND)的，且{fk，k≥1}均为单调递增的，则{fk(Xk)，k=1，2，…}都为LND(或UND)的．

(2)若{Xk，k≥1}是LND(或UND)的，且{fk，k≥1}均为单调递减的，则{fk(Xk)，k=1，2，…}都为UND(或LND)的．

(3)若{Xk，k≥1}是ND的，且{fk，k≥1}同为递增或同为递减的，则{fk(Xk)，k=1，2，…}仍为ND的．

(4)若{Xk，k≥1}是非负且为UND的，则对每一个n=1，2，…，都有

1.3 相关命题

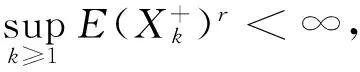
事实上，命题1是文献[5]中引理2.3的一个修改及补充．下面仅给出几处关键的修改．

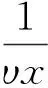
(3)将文献[5]中的C替换为

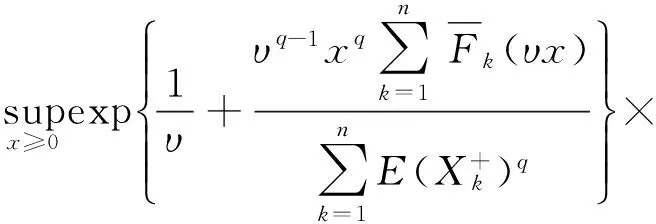
命题1在推导定理1中非随机和的下限时，将发挥重大作用．

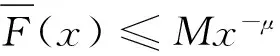
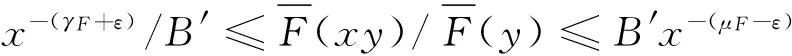
1.4 相关引理

下面给出几个重要的引理，它们都是以往精细大偏差理论中的经典结论．

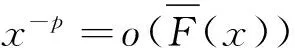
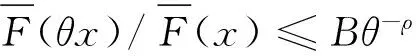
引理3假设{Yn，n≥1}是一列独立同分布(independent identical distribution,i.i.d.)的随机变量序列，有共同的均值E(Y1)=1/λ，并且构成了一个更新计数过程{N(t)，t≥0}，则对任意的正数δ和m，有

成立．

关于引理1和引理2的细节可见文献[6]，关于引理3的细节可见文献[2]．

2 主要结论

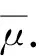
(1){Fn，n≥1}和F满足对所有x≥X0和某个X0>0一致地有

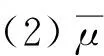
且

则对任意固定的γ>0，当x≥γn时，一致地有

其中

证明首先，估计下界．对任意的λ>1，

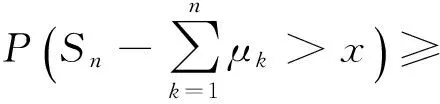
(3)

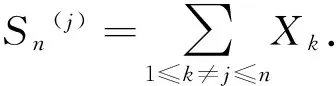
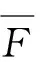
(4)

下面估计式(3)中的第2项，对所有充分大的x(x≥X0)，有

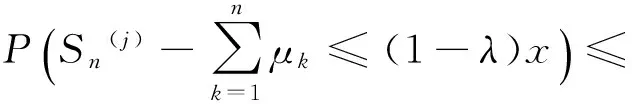
由性质1中的(2)、(3)知，随机变量序列{μk-Xk，k≥1}为UND的．因此，对任意固定的γ>0和p>γF，由命题1知，存在正数υ0和与x、n无关的C1，对所有x≥γn和所有充分大的n，一致地有

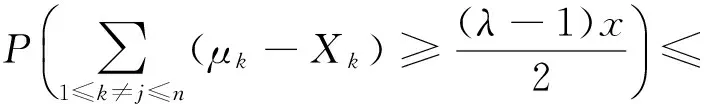
由于{Xn，n≥1}为非负随机变量序列，结合引理1可得

(5)

将式(4)和式(5)代入式(3)，可得

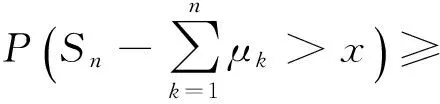
令δ1↓0，可得

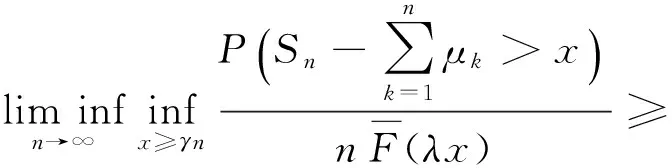
(6)

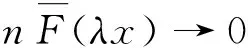
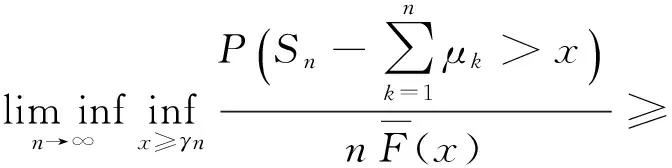
由于F∈C且λ>1是任意的，可得

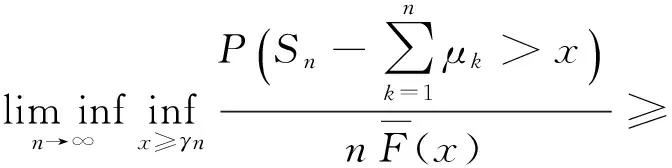
(7)

下面开始估计上界．对任意的θ∈(0，1)，定义

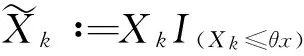
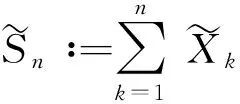
采用截断估计的方法，可得

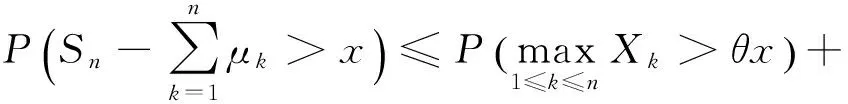
(8)

将式(4)代入式(8)中，对任意的δ2>0，有

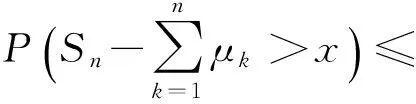
(9)

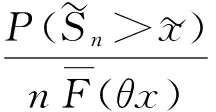
(10)

这里，在第2个不等式中使用了ND随机变量的性质1中的(4)，h的值将在后续证明中给出．下面先将式(10)中的最后一项分为两项，由不等式expx-1≤xexpx对所有的x均成立，可得对每一个k≥1，有

(11)

将式(11)代入式(10)中，对所有充分大的n及任意的δ3，δ4>0，可得

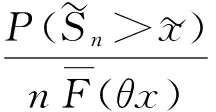
(12)

这里运用了定理1中的假设和引理2中的结论．在式(12)中取h=(a-2ρloga)/θx，对所有足够大的n和任意的δ5>0，可得

(13)

令δ2↓0，δ3↓0，δ4↓0，δ5↓0，联合式(9)和式(13)，可得

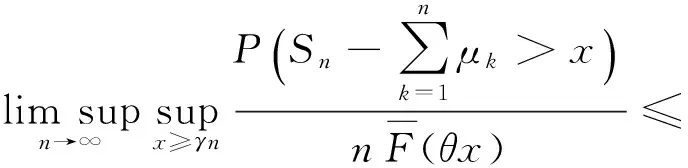
由F∈C和θ∈(0，1)的任意性，可得

(14)

最后，联合式(7)和式(14)即可得出定理1中的结论．

定理2若{Xn，n≥1}和X满足定理1中的条件，且假设{N(t)，t≥0}是一个独立于{Xn，n≥1}的非负整值过程，当t→∞时，E(N(t))=λ(t)→∞．该过程满足假设Ⅰ：对任意固定的δ>0和某一个p>γF，E(Np(t))I{N(t)>(1+δ)λ(t)}=O(λ(t)),则对任意固定的γ>0，当t→∞时，对所有的x≥γλ(t)一致地有

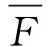
运用定理1中的结论，并采用文献[12]中定理3．2的证明方法，结合ND随机变量的性质1中的(3)，即可得到此结论．故此不再给出具体的证明．

3 应 用

本章将把定理2的结论应用到更为一般的复合更新风险模型中，并给出相应的结论．关于一般的复合更新风险模型可见文献[2]，下面给出改进后的复合更新风险模型．

(1)索赔额序列{Xn，n≥1}为非负ND的，具有分布函数列{Fn，n≥1}和有限的均值向量

μ=(E(X1)E(X2) …E(Xn) …)

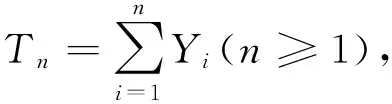
(3)由第n次事故所引发的索赔次数是一个取非负整数的随机变量Zn，并且假定{Zn，n≥1}是独立同分布的具有共同的分布函数G，独立于{Xn，n≥1}和{Yn，n≥1}．

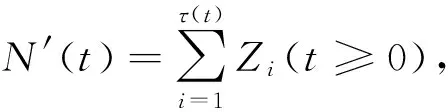
使用定理2的结论，可得到如下结论：

在上述复合更新风险模型中，若G∈C，γF<μG，且满足定理1中的条件(1)和条件(2)，则复合更新过程{N′(t)，t≥0}满足定理2中的假设Ⅰ且对任意固定的γ>E(Z)，当t→∞时，对任意的x≥γλ′(t)一致地有

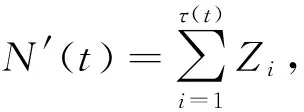
E(τp(t))I{τ(t)>(1+δ)E(τ(t))}=O(τ(t))

由于{Zn，n≥1}为独立同分布的随机变量序列，且其分布函数G∈C，很容易验证它满足定理1中的条件(1)和条件(2)．由定理2，对所有的x≥γE(τ(t))和任意固定的γ>E(Z)，一致地有

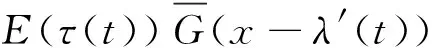
(15)

由于γF<μG，选择适当的p使得γF0，有

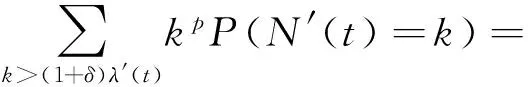
(16)

取充分小的ε>0，使得γF0，有

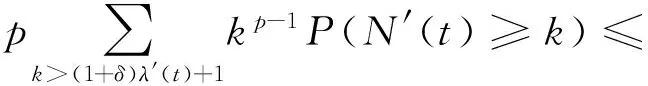
(17)

这里，在第2个不等式中利用了式(15)，在最后一个不等式中利用了命题2．同样，对任意的δ7>0，有A2≤(1+δ7)(

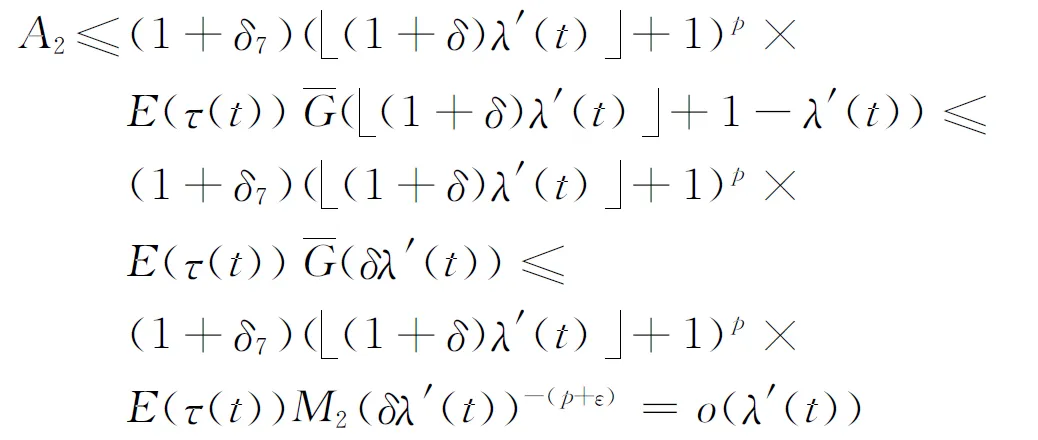
(18)

上式中的M1和M2是与k无关的非负常数．将式(17)和式(18)代入式(16)中，可得N′(t)满足定理2中的假设Ⅰ．由定理2即可得出该结论．

4 结 语

本文对不独立不同分布情形下的精细大偏差做了细致的研究．考虑到精细大偏差理论的发展前沿，本文在前人的基础上，重点解决了不独立不同分布时精细大偏差的下限问题，并建立了与以往不同的更为一般、贴近实际的复合更新风险模型．最后，将所得到的精细大偏差结论应用到该模型中，具有一定的理论与实际价值．

[1] Klüppelberg C, Mikosch T. Large deviations of heavy-tailed random sums with applications in insurance and finance [J].JournalofAppliedProbability, 1997,34(2):293-308.

[2] TANG Qi-he, SU Chun, JIANG Tao,etal. Large deviations for heavy-tailed random sums in compound renewal model [J].Statistics&ProbabilityLetters, 2001,52(1):91-100.

[4] 冯敬海,宋立新,包莹莹. 一致变化尾的随机和局部精确大偏差[J]. 大连理工大学学报, 2014,54(4):482-486.

FENG Jing-hai, SONG Li-xin, BAO Ying-ying. Local precise large deviations for random sums with consistently varying tail [J].JournalofDalianUniversityofTechnology, 2014,54(4):482-486. (in Chinese)

[5] TANG Qi-he. Insensitivity to negative dependence of the asymptotic behavior of precise large deviations [J].ElectronicJournalofProbability, 2006,11(4):107-120.

[6] Ng K W, TANG Qi-he, YAN Jia-an,etal. Precise large deviations for sums of random variables with consistently varying tails [J].JournalofAppliedProbability, 2004,41(1):93-107.

[7] TANG Qi-he. Insensitivity to negative dependence of asymptotic tail probabilities of sums and maxima of sums [J].StochasticAnalysisandApplication, 2008,26(3):435-450.

[8] HE Wei, CHENG Dong-ya, WANG Yue-bao. Asymptotic lower bounds of precise large deviations with nonnegative and dependent random variables [J].Statistics&ProbabilityLetters, 2013,83(1):331-338.

[9] LU Da-wei, SONG Li-xin, XU Ying. Precise large deviations for sums of independent random variables with consistently varying tails [J].CommunicationsinStatistics-TheoryandMethods, 2014,43(1):28-43.[10] CHEN Yu, ZHANG Wei-ping. Large deviations for random sums of negatively dependent random variables with consistently varying tails [J].Statistics&ProbabilityLetters, 2007,77(5):530-538.

[11] Kass R, TANG Qi-he. A large deviation result for aggregate claims with dependent claim occurrences [J].Insurance:MathematicsandEconomics, 2005,36(3):251-259.

[12] WANG Shi-jie, WANG Wen-sheng. Precise large deviations for sums of random variables with consistently varying tails in multi-risk models [J].JournalofAppliedProbability, 2007,44(4):889-900.

[13] Bingham N H, Goldie C M, Teugels J L.RegularVariation[M]. Cambridge:Cambridge University Press, 1987.

[14] Block H W, Savits T H, Shaked M. Some concepts of negative dependence [J].TheAnnalsofProbability, 1982,10(3):765-772.

Preciselargedeviationsforcompoundrenewalriskmodelwithnegativedependenceclaims

SONG Li-xin1, FENG Jing-hai1, YUAN Liang-liang*1, SHI Xin-yong1,2

( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China；2.Troops 68048, The Chinese People′s Liberation Army, Baoji 721013, China )

The precise large deviations of non-independent and non-identical distributions are investigated, where {Xn,n≥1} is a sequence of negative dependence random variables with distribution functions {Fn,n≥1}. Under certain conditions, the lower bound of the precise large deviations for the non-random sums is solved, and the uniformly asymptotic results for the corresponding random sums are obtained. The research results are applied to the more practical compound renewal risk model, and the theoretical and practical values are verified.

precise large deviations; negative dependence; random sums; compound renewal risk model

1000-8608(2014)06-0696-06

2014-05-13；

: 2014-07-22．

国家自然科学基金资助项目(11101061,11371077,61175041).

宋立新(1966-)，男，教授，博士生导师，E-mail:lxsong@163.com；袁亮亮*(1989-)，男，硕士生，E-mail:llyuan_dlut@163.com.

O211.4

：Adoi:10.7511/dllgxb201406015