Hom-结合超代数的表示和上同调

南 基 洙， 王 春 月,2， 张 庆 成

( 1.大连理工大学 数学科学学院， 辽宁 大连 116024；2.吉林工程技术师范学院 应用理学院， 吉林 长春 130052；3.东北师范大学 数学与统计学院， 吉林 长春 130024 )



Hom-结合超代数的表示和上同调

南 基 洙1， 王 春 月1,2， 张 庆 成*3

( 1.大连理工大学 数学科学学院， 辽宁 大连 116024；2.吉林工程技术师范学院 应用理学院， 吉林 长春 130052；3.东北师范大学 数学与统计学院， 吉林 长春 130024 )

Hom-结合超代数；表示；上同调

0 引 言

结合超代数对很多代数结构研究都具有重要的作用．研究者对结合超代数的研究越来越感兴趣．Ayadi等研究了具有非退化、超对称、不变双线性型结合超代数的结构和双扩张[1]．Montaner给出了结合超代数的理想与Lie超代数的理想之间的关系[2]．Laliena等研究了具有超对合的结合超代数结构与具有反对称元素的Lie代数结构之间的关系[3]．

Hom-代数结构首先出现在Lie代数拟形变中．近年来，关于Hom-代数结构已经涌现了很多研究结果[4-7]．Ammar等给出了Hom-结合代数的上同调群[8]．Makhlouf等研究了Hom-结合代数的低阶上同调群[9]．而Ammar等在研究Hom-Lie超代数和Hom-Lie可许超代数的结构时提出了Hom-结合超代数的定义[10]，它对研究Hom-Lie超代数起着重要的作用．对于Hom-结合超代数还有许多问题值得研究．本文将Hom-结合代数的上同调群推广到Hom-结合超代数，主要研究Hom-结合超代数的表示和上同调．

1 基本概念

首先研究Hom-结合超代数的一些基本性质，给出Hom-结合超代数表示的定义．

本文中所有的超线性空间和超代数都是复数域上的超线性空间和超代数，齐次元素x的次数记为|x|．

定义1[2]设A是一个超线性空间，∘:A×A→A是一个偶双线性映射，φ:A→A是一个偶线性映射．对任意的x，y，z∈A，满足

(x∘y)∘φ(z)=φ(x)∘(y∘z)

则称(A，∘，φ)是一个Hom-结合超代数．

设(A1，∘1，φ1)和(A2，∘2，φ2)是两个Hom-结合超代数，f:A1→A2是一个偶线性映射．若f满足

f(x∘1y)=f(x)∘2f(y)，fφ1=φ2f

称偶线性映射f是一个Hom-结合超代数的同态．

注当φ=id时，Hom-结合超代数是结合超代数．若偶线性映射φ:A→A满足φ(x∘y)=φ(x)∘φ(y)，则称(A，∘，φ)是一个保运算的Hom-结合超代数．

下面定理给出了由一个结合超代数和一个偶的结合超代数自同态构造一个Hom-结合超代数的方法．

定理1设(A，∘)是一个结合超代数，φ:A→A是一个偶的结合超代数自同态，任取x，y∈A，定义运算x∘φy=φ(x∘y)，则(A，∘φ，φ)是一个Hom-结合超代数．

证明任取x，y，z∈A，则

(x∘φy)∘φφ(z)=φ2((x∘y)∘z)=φ2(x∘(y∘z))=φ(x)∘φ(y∘φz)

因此(A，∘φ，φ)是一个Hom-结合超代数．

e0∘e0=k1e0，e0∘e1=k1e1，

e1∘e0=k1e1，e1∘e1=k2e0；k1，k2≠0

然而(A，∘φ)不是一个结合超代数．事实上，当a≠±1时，

(e0∘φe1)∘φe1=k1k2e0≠e0∘φ(e1∘φe1)=a2k1k2e0；

(e1∘φe1)∘φe0=a2k1k2e0≠e1∘φ(e1∘φe0)=k1k2e0

命题1设(A1，∘1，φ1)和(A2，∘2，φ2)是两个Hom-结合超代数，对任意a1，a2∈A1，b1，b2∈A2，定义一个偶双线性映射：

∘：(A⊕B)×(A⊕B)→(A⊕B)

(a1+b1)∘(a2+b2)=a1∘1a2+b1∘2b2

对任意a∈A1，b∈A2，定义一个偶映射

(φ1+φ2)：A1⊕A2→A1⊕A2

(φ1+φ2)(a+b)=φ1(a)+φ2(b)

则(A1⊕A2，∘，φ1+φ2)是一个Hom-结合超代数．

证明显然A1⊕A2是一个超线性空间，φ1+φ2是一个偶线性映射．任取a1，a2，a3∈A1，b1，b2，b3∈A2，由(A1，∘1，φ1)和(A2，∘2，φ2)是两个Hom-结合超代数，则有

((a1+b1)∘(a2+b2))∘((φ1+φ2)(a3+b3))=(a1∘1a2)∘1φ1(a3)+(b1∘2b2)∘2φ2(b3)=φ1(a1)∘1(a2∘1a3)+φ2(b1)∘2(b2∘2b3)=((φ1+φ2)(a1+b1))∘((a2+b2)∘(a3+b3))

因此(A1⊕A2，∘，φ1+φ2)是一个Hom-结合超代数．

定义2设(A，∘，φA)是一个Hom-结合超代数，V是一个超线性空间，φV：V→V是V的一个偶线性映射．在V上定义线性运算·：A×V→V，(x，v)x·v，使得下列条件成立：任取x，y∈A，v∈V，

(1)x·v∈Vθ+μ， ∀x∈Aθ，∀v∈Vμ；

(2)φV(x·v)=φA(x)·φV(v)；

(3)(x∘y)·φV(v)=φA(x)·(y·v)称(V，·，φV) 是一个Hom-左A-模．

同样可以定义Hom-右A-模．

定义3设(A，∘，φA)是一个Hom-结合超代数，V是一个超线性空间，φV：V→V是V的一个偶线性映射．在V上定义线性运算·：V×A→V，(v，x)v·x，使得下列条件成立：任取x，y∈A，v∈V，

(1)v·x∈Vθ+μ，∀x∈Aθ，∀v∈Vμ；

(2)φV(v·x)=φV(v)·φA(x)；

称(V，·，φV)是一个Hom-右A-模．

若(V，·，φV)既是一个Hom-左A-模又是一个Hom-右A-模，且满足

φA(x)·(v·y)=(x·v)·φA(y)

则称(V，·，φV)是一个Hom-A-双模．

例2(A，∘，φA)是一个Hom-A-双模．

例3设A是一个结合超代数，(V，·)是一个A-双模，则(V，·)也是一个Hom-A-双模．事实上，相当于φV=idV．

定义4设(A，∘，φA)是一个Hom-结合超代数，V是一个超线性空间，φV：V→V是一个偶线性映射．如果偶线性映射ρφV：A→gl(V)满足下列条件：

(1)ρφV(φA(x))φV=φVρφV(x);

本次研究中接受放疗治疗的71例肿瘤患者应用CT模拟定位扫描技术均实现了准确定位靶区，且病灶区域、靶区及毗邻组织的界限清晰，疗程结束后复查CT，并判定疗效，结果显示符合完全缓解的有26例，占36.62%，符合部分缓解的有42例，占59.15%，总有效率达到了95.77%，但仍有2例稳定，1例进展。患者放疗期间均未见严重不良反应及并发症。

(2)ρφV(x∘y)φV=ρφV(φA(x))ρφV(y)

则称ρφV是关于φV的(A，∘，φA)在V上的一个表示．

如果定义ρφV(x)(v)=x·v(或ρφV(x)(v)=(-1)|x||v|v·x)，则Hom-左(右)A-模(V，φV)与表示ρφV一一对应．

命题2设(A1，∘1，φ1)和(A2，∘2，φ2)是两个Hom-结合超代数，φ：A2→A1是一个偶的Hom-结合超代数的同态，(V，·，φV)是任意一个Hom-A1-双模．任取a2∈A2，v∈V，定义

a2·′v=φ(a2)·v，v·′a2=v·φ(a2)

则(V，·′，φV)是一个Hom-A2-双模．

证明任取v∈V，a2，b2∈A2，则有

φV(a2·′v)=φV(φ(a2)·v)=φ1(φ(a2))·φV(v)=φ(φ2(a2))·φV(v)=φ2(a2)·′φV(v)；

(a2∘2b2)·′φV(v)=φ(a2∘2b2)·φV(v)=(φ(a2)∘1φ(b2))·φV(v)=φ2(a2)·′(b2·′v)

因此(V，·′，φV)是一个Hom-左A2-模．

同理可证(V，·′，φV)是一个Hom-右A2-模．

又因为

φ2(a2)·′(v·′b2)=φ(φ2(a2))·(v·φ(b2))=φ1(φ(a2))·(v·φ(b2))=(φ(a2)·v)·φ1(φ(b2))=(φ(a2)·v)·φ(φ2(b2))=(a2·′v)·′φ2(b2)

所以(V，·′，φV)是一个Hom-A2-双模．

2 Hom-结合超代数的上同调

下面将给出Hom-结合超代数上同调的定义．本章中所有的Hom-结合超代数都是保运算的Hom-结合超代数．对所有齐次元素(a1，a2，…，an)∈An，记

|(a1，a2，…，an)|=|a1|+|a2|+…+|an|

定义5设(A，∘，φA)是一个Hom-结合超代数，(V，·，φV)是一个Hom-A-双模．如果齐次n-线性映射f：⊗nA→V满足

(1)f(a1，a2，…，an)∈Vα，其中|f|+|a1|+|a2|+…+|an|=α；

(2)f(a1，a2，…，ai，ai+1，…，an)=-(-1)|ai||ai+1|f(a1，a2，…，ai+1，ai，…，an)；

(3)φV(f(a1，a2，…，an))=f(φA(a1)，φA(a2)，…，φA(an))

定义6设(A，∘，φA)是一个Hom-结合超代数，(V，·，φV)是一个Hom-A-双模．定义一个偶线性映射

为

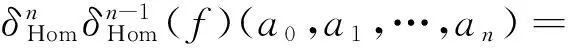
定义7

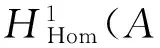
3 结 语

本文给出了Hom-结合超代数的表示和双模的定义，并以此研究了Hom-结合超代数的上同调．

[1] Ayadi I, Benayadi S. Associative superalgebras with homogeneous symmetric structures [J].CommunicationinAlgebra, 2012,40(4):1234-1259.

[2] Montaner F. On the Lie structure of associative superalgebras [J].CommunicationinAlgebra, 1998,26(7):2337-2349.

[3] Laliena J, Sacristan S. On certain semiprime associative superalgebras [J].CommunicationinAlgebra, 2009,37(10):3548-3552.

[4] Makhlouf A, Silvestrov S. Hom-algebra structure [J].JournalofGeneralizedLieTheoryandApplications, 2008,2(2):51-64.

[5] SHENG Yun-he. Representations of Hom-Lie algebras [J].AlgebrasandRepresentationTheory, 2012,15(6):1081-1098.

[6] Yau D. Hom-algebras and homology [J].JournalofLieTheory, 2009,19(2):409-421.

[7] Yau D. Enveloping algebras of Hom-Lie algebras [J].JournalofGeneralizedLieTheoryandApplications, 2008,2(2):95-108.

[8] Ammar F, Ejbehi Z, Makhlouf A. Cohomology and deformations of Hom-algebras [J].JournalofLieTheory, 2011,21(4):813-836.

[9] Makhlouf A, Silvestrov S. Notes on formal deformations of Hom-associative and Hom-Lie algebra [EB/OL]. (2007-12-19) [2013-12-15]. http://arXiv.org/abs/0712.3130v1.

[10] Ammar F, Makhlouf A. Hom-Lie superalgebras and Hom-Lie admissible superalgebras [J].JournalofAlgebra, 2010,324(7):1513-1528.

RepresentationandcohomologyofHom-associativesuperalgebras

NAN Ji-zhu1， WANG Chun-yue1,2， ZHANG Qing-cheng*3

( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China；2.School of Applied Sciences, Jilin Teachers′ Institute of Engineering and Technology, Changchun 130052, China；3.School of Mathematics and Statistics, Northeast Normal University, Changchun 130024, China )

Hom-associative superalgebras; representation; cohomology

1000-8608(2014)06-0702-05

2014-01-04；

: 2014-08-04．

高等学校博士学科点专项科研基金资助项目(201101647)；吉林省自然科学基金资助项目(20130101068).

南基洙(1965-)，男，教授，E-mail:jznan@163.com；王春月(1979-)，女，博士生，E-mail:wang1chun2yue3@163.com；张庆成*(1960-)，男，教授，E-mail:zhangqc569@nenu.edu.cn.

O152.5

：Adoi:10.7511/dllgxb201406016