吸振器底座对减振效果的影响研究

徐振邦，吴清文

(中国科学院 长春光学精密机械与物理研究所，长春 130033)

柔性结构由于其质量轻的优点，被广泛用于航天、航天设备中。柔性结构应用中的最大困难来自于弹性模态共振。因此，能够抑制柔性结构共振的技术成为了振动控制领域的研究热点之一。吸振器技术就是一种能够有效抑制结构弹性模态共振的振动控制技术，该技术具有使用方便、效果好等优点。

柔性结构由于其自身特性，在一定频率范围内通常具有多阶弹性模态。若仅某一阶模态需要进行控制，则可将柔性结构等效为单自由度结构，其控制方法相对成熟[1]。因此该领域的研究大部分集中在多模态控制方面，适用的吸振器技术包括多吸振器[2-4]，多自由度吸振器[5-6]以及主动[7-8]或半主动吸振器[9-10]技术。多吸振器技术使用多个吸振器来控制结构的多阶模态。通过多个吸振器的共同作用拓展减振带宽。文献[2]中具体研究了该技术的作用机理，其研究结果表明：在窄带内，主结构和吸振器的交互作用是主导因素，而在较宽的频带内，吸振器的阻尼主导其性能。多自由度吸振器是一种相对新颖的振动抑制技术，该技术利用多自由度吸振器振子的特性来衰减系统的多阶模态共振。当吸振器振子为刚体时，该技术最多能衰减系统的六阶模态[5]，当吸振器振子为弹性体[6]时，能够控制更多阶弹性模态。多模态吸振器比其他类型吸振器的影响参数更多，因此多个参数的优化设计为该技术的重点研究内容。半主动和主动吸振器具有可调的结构或控制参数，因此这两种技术的有效带宽更宽，减振效果更好，但技术的复杂度较高，影响了技术可靠性。

调研中发现，该领域的研究中普遍将吸振器的底座忽略，或将其简单的等效为集中质量点，当减振对象为刚性时，这种方式是合理的。但当减振对象为柔性结构时，底座的刚度和质量就将对结构产生影响，在这种情况下，上述处理方式就不在适合。为此，本文重点研究了吸振器底座对其减振效果的影响，并进一步通过理论和仿真分析考察不同底座参数对减振效果的影响情况。

1 理论建模

图1为带有底座吸振器的系统模型图。用两端固支的弹性梁作为减振对象，其上安装带有底座吸振器。有底座吸振器由底座和其上的单自由度阻尼弹性结构构成。建模中，吸振器底座采用刚性质量块模拟，在底座和梁之间采用多个刚性点连接的方式模拟刚性较强的螺栓连接。柔性梁主系统中各位置处的振动情况不同，因此采用功率流表征主系统的整体振动情况[11-12]。通过考查输入到弹性梁中的功率流变化来考察吸振器的减振效果。

图1 仿真模型图

图1所示结构可看作由两级子系统构成：第一级子系统由弹性梁及附加其上的有底座吸振器构成；第二级子系统为有底座吸振器，该系统可看作是在底座上附加单自由度结构构成的。二级系统具有数学上的相似性，因此下面的推导中首先建立在某一结构上附加N个子结构的一般性动力学方程，进而推导出图1所示结构的数学模型。

设某系统激励点的原点导纳为Zp，在该系统上安装N个导纳为Hs的子系统，对整个系统有：

(1)

其中;Vp为激励点处的速度矢量，Vs为子系统安装点处的速度矢量，Zps为主系统上激励点和子系统安装点之间的导纳矩阵，Zss为主系统上各子系统安装点间的导纳矩阵，Fp为系统激励力，Fs为N个子结构施加给主系统的作用力。对N个子系统有：

Vs=-DFs

(2)

式(2)中D=diag(Hs)N×N，联立方程(1)，(2)得：

[Zp+ΔZ]Fp

(3)

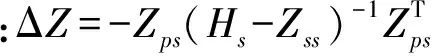
Vs=-DZps-1ΔZFp,Fs=Zps-1ΔZFp

(4)

利用式(3)，(4)即可求得系统中各个环节处的振动响应。据此进一步求得系统中各个环节处的功率流情况。外界输入到整个系统的总功率流为：

(5)

由主系统传入到N个子系统的功率流为：

(6)

以上两者之差即为残留在主系统的净功率流：

P=Pin-Pout

(7)

尽量减少这部分功率流就是吸振器的减振目标。

下面在以上推导的基础上，求出图1所示结构的数学模型。首先推导有底座吸振器的数学模型。该吸振器可看成在质量块上附加一个单自由度结构组成。根据以上推导，先求出质量块的导纳矩阵。刚性质量块上任意两点间的导纳为：

(8)

式中:M为质量块质量，J为质量块绕质心的转动惯量，xp和xq为质量块上两点相对于质心的位置坐标，为激励力的角频率。在五点安装的情况下，质量块的导纳为：

(9)

(10)

式中:xe为吸振器安装点的位置坐标，为单自由度结构的导纳，具体表达式如下：

(11)

其中:ka为单自由度结构的弹簧刚度，ma为振子的质量，ca为弹簧阻尼。下面推导梁和有底座吸振器耦合系统的方程。两端固支梁上任意两点间的导纳为：

(12)

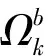
Zp=Zls(xf,xf)

(13)

(14)

(15)

(16)

吸振器的减振效果可采用有、无吸振器时，输入到系统中的净功率流之比来保证，具体计算方法如下：

(17)

式(17)中，Pwith为安装吸振器后输入到系统中的净功率流，Pwithout为未安装吸振器时输入到系统中的净功率流。

2 仿真结果

下面介绍仿真研究结果。仿真中弹性梁的尺寸设为1 m×0.05 m×0.005 m，密度为7 800 kg/m3，弹性模量为2.0×1011Pa，泊松比为0.3，质量为1.95 kg。计算得到弹性梁的前两阶固有频率分别为：

f1=27.3 Hzf2=75.3 Hz

2.1 有、无底座吸振器减振效果比较

首先比较有、无底座吸振器的减振性能。设两种吸振器的总质量均为0.2 kg，对于无底座吸振器来说，其总质量即为动子质量。有底座吸振器的底座将占据部分质量，设为0.04 kg，则动子质量为0.16 kg。底座尺寸设为0.1 m。

系统一阶固有频率的影响通常最大，因此两种吸振器的参数都针对一阶固有频率进行设计。根据经典的不动点优化方法[13]计算得到的吸振器最佳调谐频率和阻尼比为：

fa=24.8 Hzζ=0.167

有底座吸振器通过三个安装点和底座固连。三个安装点在底座上平均分布。计算中以位于中间的安装点的位置作为吸振器的安装位置。为求一般性，计算中激励施加在0.25 m处，在该处施加激励，能够激发出系统的两阶固有频率。吸振器安装在和激励位置相同的位置。

图2为两种吸振器减振特性的比较。图2(a)为采用公式(17)表征的吸振器减振效果。图2(b)为输入系统的功率流。由图2(a)可见，在系统的一阶固有频率处两种吸振器都能取得很好的减振效果，且无底座吸振器的减振效果要好于有底座吸振器，其原因是无底座吸振器的质量都集中在振子上，质量利用率更高。在系统一、二阶固有频率(包括二阶固有频率)之间的较宽频带内，有底座吸振器的减振效果明显优于无底座吸振器。在系统二阶频率以上，有底座吸振器出现负效果。

图2 减振特性比较

以上现象可以通过图2(b)解释。安装有底座吸振器后，将导致系统的二阶共振峰向高频移动，从而使得系统一、二阶固有频率之间的频带内的振动出现了明显衰减。有底座吸振器的这种特点，可以用来拓展吸振器的有效减振带宽，但是这种方法会使得高频段内的振动增加，因此采用这种方法的前提是要对激励力的频率分布有所了解。由图2(b)中的三条曲线对比可见，有底座吸振器同无底座吸振器的不同之处主要有三点：一阶频率处的减振效果ΔP1，系统二阶峰值的衰减ΔP2以及二阶峰值的偏移Δf。这三个参数可作为有底座吸振器减振效果的表征。

2.2 吸振器安装位置对减振效果的影响

下面考查吸振器的安装位置对减振效果的影响。图3(a)为无底座吸振器的减振效果三维图。由图3可见：对于系统一阶频率的振动，吸振器安装在任何位置均能起到一定的减振效果，安装在系统一阶振动的峰值位置(0.5 m)处效果最好；对于系统二阶频率的振动，吸振器安装在二阶模态的峰值位置处(0.3 m和0.7 m)最好。对于其他频段内的振动，无底座吸振器基本没有效果。图3(b)为有底座吸振器的减振效果三维图，由图可见：对于系统一、二阶模态的振动，同无底座吸振器一样，安装在峰值位置处效果最好。对于系统一、二阶频率之间频段的振动，有底座吸振器也能起到一定的减振效果，其安装在系统二阶峰值处的减振效果最为明显，且安装在0.3m处的效果要好于安装在0.7 m处。

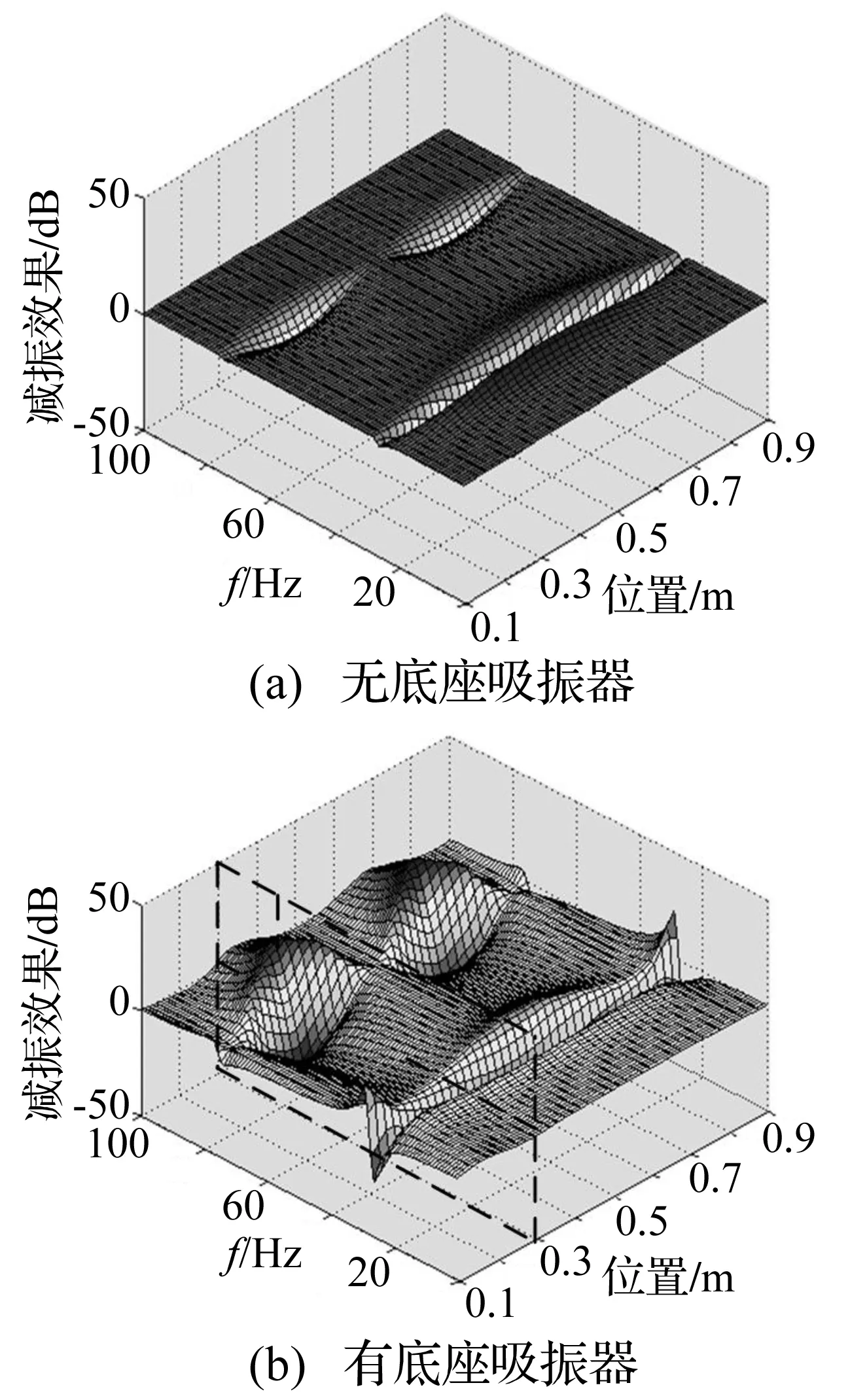
图3 吸振器安装位置对减振效果的影响

2.3 吸振器动质量和静质量之比对减振效果的影响

有底座吸振器的质量不是全部集中在振子上，因此需要考虑吸振器的动质量和静质量之比(动静比)对减振效果的影响。

图4为动静比不同时有底座吸振器三个指标的变化。由图4可见，随着动静比的提高，系统的一阶、二阶的减振效果均有所提高，并且开始时系统减振效果提高较快，但到了一定程度后，继续增大动静比对系统减振效果的提高影响不大。动静比的提高能够加大二阶峰值的偏移程度，从而拓展吸振器的减振带宽，这一现在产生的原因是：底座质量等效增加了主系统二阶模态质量，从而使得系统二阶峰值向低频移动，并且质量越小，低频移动的越少。但动静比达到一定范围后，继续提高变化不明显。这说明，在设计吸振器底座时，要尽量减小吸振器的底座质量，但过于减小对效果的进一步提高无益，反而会影响底座刚度。

2.4 底座尺寸对减振效果的影响

图5为吸振器底座尺寸不同时，三个指标的变化情况。当吸振器的底座尺寸为0时，吸振器底座退化为集中质量点。

由图5可见，增加底座尺寸对系统一阶频率处的效果影响很小，因此若仅考虑用吸振器控制系统一阶频率，底座尺寸的影响可以忽略。尺寸增加会使得系统二阶频率处的减振效果略有提高。但改善不明显。底座尺寸的增加会导致二阶峰值的偏移范围加大，因此若要拓展吸振器的有效带宽，底座尺寸应尽量加大。但底座尺寸加大时，会影响底座刚度，因此要综合考虑。

2.5 连接点个数的影响

吸振器底座和梁之间连接点的个数将影响两者的连接刚度，安装点数越多，连接刚度越大。下面考查不同安装点个数对减振效果的变化。

由图6可见，增加安装点个数对一阶、二阶固有频率处的减振效果影响较小。对于频率偏移，二个安装点时，系统的二阶频率没有偏移，其原因如下：仅有两个安装点时，弹性梁的局部振型不会被底座所改变，因此其局部刚度未发生改变，也就不会产生频率偏移。三、四、五个安装点时，峰值的偏移程度基本一致。这说明有底座吸振器的安装点个数三个就能够满足需求。

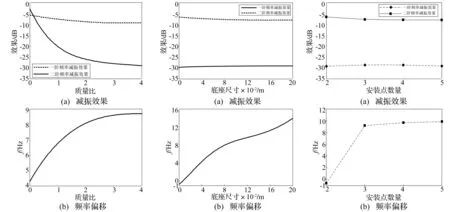
图4 底座质量对减振效果及频率偏移的影响

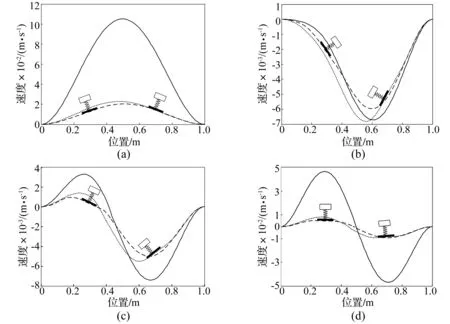
——不安装吸振器；------吸振器安装在0.3m处；——吸振器安装在0.7 m处

2.6 对振幅的衰减效果

以上仿真中均考察的是对系统输入净功率流的影响，工程上有时更关心系统的振幅衰减情况。图7(a～d)显示在激励频率分别为27 Hz、46 Hz、60 Hz和75 Hz四种典型情况下，系统的加速度振幅响应情况。由图7可见，在27～75 Hz的频率范围内，安装有底座吸振器后，均能起到一定的减振效果。在系统一阶及二阶固有频率处的减振效果最为明显。安装在梁0.3 m处的吸振器的减振效果略好于安装在0.7 m处，特别是在45 Hz及60 Hz的中间频段处。

3 结 论

本文研究了吸振器底座对吸振器减振性能的影响。研究结果表明：通过合理设计吸振器底座，能够拓展吸振器的有效减振带宽。底座的安装位置、质量比、尺寸以及连接点个数等因素都会对减振性能造成影响，一般而言，底座的质量越小，尺寸越大，连接点个数越多，其效果越好，但一味增加这些参数指标，并不会给减振效果带来太大改善。因此在设计吸振器底座时，要对以上参数进行合理设计，以便实现减振效果的最优化。

以上结论均是在吸振器的底座刚度较大，可以等效为刚体质量时取得的。底座柔性较大，不能视为刚体的情况，需要进一步研究。

[1] 姚斌辉,上官文斌.被减振物体连接于弹性地基时动力吸振器的设计[J].振动与冲击,2012,31(7):58-62.

YAO Bin-hui, SHANGGUAN Wen-bin. Design of vibration absorber for a body mounted on a flexible foundation[J]. Journal of Vibraiton and Shock, 2012,31(7):58-62.

[2] Yang C, Li D, Cheng L. Dynamic vibration absorbers for vibration control[J]. Journal of Sound and Vibration, 2011, 330: 1582-1598.

[3] Dayou J, Brennan M J. Optimum tuning of a vibration neutralizer for Optimum tuning of a vibration neutralizer[J]. Proc Instn Mech Engrs, 2001,215(C):933-942.

[4] 吴崇健, 骆东平, 杨叔子,等. 离散分布式动力吸振器的设计及在船舶工程中的应用[J]. 振动工程学报, 1999, 12(4): 584-589.

WU Chong-jian, LUO Dong-ping, YANG Shu-zi, et.al. Design and application of multiple tuned mass damper for ships[J]. Journal of Vibration Engineering, 1999, 12(4): 584-589.

[5] Verdirame J M, Nayfeh S A, Zuo L. Design of multi-degree-of-freedom tuned-mass dampers[J]. Smart Structures and Materials 2002: Damping and Isolation, 2002, 4697: 98-108.

[6] Zuo L. Effective and robust bibration effective and robust bibration tuned-mass dampers[J]. Journal of Vibration and Acoustics, 2009, 131: 1-11.

[7] Cheung Y L, Wong W O, Cheng L. Optimization of a hybrid vibration absorber for vibration control of structures under random force excitation[J]. Journal of Sound and Vibration, 2013, 332: 494-509.

[8] Keas P J, Dunham E, Lampater U, et al. Active damping of the SOFIA telescope assembly[J]. Ground-based and Airborne Telescopes IV, SPIE, 2012, 8444: 1-15.

[9] 徐振邦, 龚兴龙, 陈现敏. 机械式频率可调动力吸振器及其减振特性[J]. 振动与冲击, 2010, 29(2): 1-6.

XU Zhen-bang, GONG Xin-long, CHEN Xian-min. Mechanical vibration absorber with tunable resonant frequency and its vibration attenuation characteristics[J]. Journal of Vibraiton and Shock, 2010, 29(2): 1-6.

[10] Deng H X, Gong X L, Wang L H. Development of an adaptive tuned vibration absorber with magnetorheological elastomer[J]. Smart Materials and Structures, 2006, 15(5): N111-N116.

[11] 王全娟, 陈家义, 李继民. 基于功率流方法的多自由度系统吸振控制[J]. 声学学报, 2002, 27(3): 277-281.

WANG Quan-juan, CHEN Jia-yi, LI Ji-min. Vibration absorption control of multi-degrees-of-freedom system on power flow[J]. Acat Acustica, 2002, 27(3): 277-281.

[12] 苑敏红, 王敏庆, 盛美萍,等. 力偶作用下薄板的吸振控制研究[J]. 机械科学与技术, 2007, 26(1): 68-71.

YUAN Min-hong, WANG Min-qing, SHENG Mei-ping, et al. Vibration absorption control of a thin plate under force-coupling[J]. Mechanical Science and Technology, 2007, 26(1): 68-71.

[13] Den J P, Mechanical Vibrations[M]. 2nd ed., McGraw-Hill, New York, 1940.