阻尼对摩擦力作用下转子系统弯扭耦合振动特性的影响

花纯利，塔 娜，饶柱石

(上海交通大学 振动、冲击噪声研究所 机械系统与振动国家重点实验室，上海 200240)

燃气轮机、航空发动机、船舶轴系及各种电动机等旋转机械被广泛地用于诸多工业生产部门中，因此旋转机械的各种异常振动都有可能严重威胁机械的安全运转，甚至可能导致重大的安全事故。旋转机械的振动破坏事故往往是弯扭振动共同作用的结果，弯曲振动和扭转振动同时存在于旋转机械的转子系统上,它们之间相互耦合,表现出复杂的非线性动力学特征。因此，研究转子系统在摩擦力作用下表现出的复杂非线性动力学特性对优化转子系统设计和故障诊断都具有十分重要的意义。

对转子系统碰摩的研究，已有大量的研究成果。尤其是自上个世纪八十年代以来，许多学者从实验、数值模拟和理论分析等方面对转子系统的碰摩响应特性展开了广泛深入的研究，并发现同频全周碰摩运动、“跳跃”现象、准周期的局部碰摩运动以及混沌行为[1-5]。转子系统的弯曲振动与扭转振动之间存在耦合关系，且其振动特性是弯扭耦合振动共同作用的结果。Tondl[6]于1965年率先提出了弯曲和扭转振动相互耦合的理论,他通过对转子系统稳定性的分析研究发现在一些转速区间内由不平衡引起的振动是不稳定的。Kato等[7]在Jeffcott转子系统弯扭耦合振动模型中考虑了质量不平衡影响而忽略了重力因素，研究表明质量不平衡是引起弯扭耦合的主要因素。刘占生等[8]对Jeffcott 转子的非线性弯扭耦合振动微分方程进行了理论分析,得出了在弯扭组合共振区内弯曲振动和扭转振动的频率特征。Al-Bedoor[9], Yuan等[10]对碰摩转子系统的瞬态振动响应特性进行了研究，通过对弯扭耦合模型中弯曲振动响应分析，指出扭转振动对转子系统整体动态特性的影响。Patel等[11]以裂纹转子为研究对象，建立了弯扭耦合振动的非线性运动方程，通过数值仿真发现考虑弯扭耦合后裂纹转子弯曲振动响应中出现一些新的频率成分。韩放等[12]通过分析考虑非线性油膜力作用下叶片-转子-轴承系统的弯扭耦合振动特性，发现系统中蕴含的一些复杂非线性动力学现象。

到目前为止，大部分研究分析中都没有涉及橡胶轴承的超弹性材料特性及摩擦力与相对滑动速度相关特性，势必影响分析结果的准确性，因此有必要进一步研究摩擦力作用下转子-橡胶轴承系统弯扭耦合振动特性。国内外船舶和深井泵等设备中大量使用了橡胶轴承，在运转过程中特别是在低速重载的工况下常常会出现异常的剧烈振动和鸣音以及橡胶体的磨损较为严重的现象，这些现象是与橡胶轴承支承的整个转子系统的静态特性和动态响应密切相关的。本文将以橡胶轴承支撑的转子系统为对象，建立摩擦力作用下转子系统弯扭耦合非线性动力学模型，并通过数值计算研究系统蕴含的各种复杂非线性动力学行为，为转子系统异常剧烈振动以及噪声机理研究提供新思路。

1 模型与运动方程的建立

1.1 摩擦模型

合理的摩擦力学模型是研究转子-轴承系统在摩擦力作用下动态特性的关键。为了能够准确描述转子和橡胶轴承间的摩擦行为以及相对低速情况下出现的自激振动现象，本文采用指数模型来描述低转速工况下的滑动摩擦特性，该模型已在液体润滑轴承中得到广泛验证，其表达式为：

(1)

式中;μs为静摩擦因数，μc为库伦摩擦因数，υ为转子与轴承间的相对滑动速度，λ为衰减系数，sgn(·)为符号函数。

由于摩擦力和摩擦力矩引起转子弯曲振动和扭转振动，则转子和轴承之间的相对滑动速度υ如下式所示：

(2)

1.2 转子系统动力学模型

转子系统模型如图1所示，质量为m转动惯量为J的三自由度刚性转盘支撑在刚度为k，阻尼为c，扭转刚度为kt,扭转阻尼为ct的无质量的弹性轴上。转子和轴承之间的间隙为δ，转子的质心与其几何中心的距离偏心距为e。图中，o1为轴承形心位置，o2为转子形心位置，o3为转子质心位置，并建立以轴承形心为原点的xo1y固定坐标系。

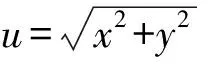
考虑到橡胶轴承具有非线性特征，计算时同时计入了支承刚度的非线性特性。由于目前尚无实验数据和理论来准确描述橡胶轴承的支撑刚度特性，因此，其非线性载荷-变形关系参照德国国防军舰艇建造规范(BV043)，并按下式进行估算：

F=krr+αr2

(3)

其中:F为载荷；r为变形量；kr为轴承刚度值。因此，轴承内环面上转子-轴承间接触刚度为kr+αr。

则转子和橡胶轴承之间的摩擦力和接触力为：

(4)

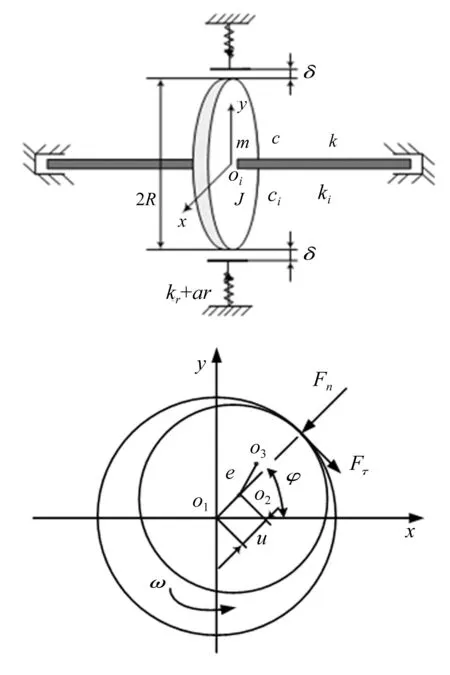
图1 转子系统模型

将摩擦力和接触力分解到笛卡尔坐标系 中为：

(5)

式中Θ为Heaveside函数即：

可以看出，碰摩力是转子位移的非线性函数，转子在运动过程中将有可能出现不稳定。摩擦力的存在使转子在碰摩点处受到对转子形心的摩擦力矩M，有

M=-FτR=-ΘμbFnR

(6)

转子系统运动是由其平动和转动这两种运动形式的合成，由拉格朗日方法可推导出在摩擦力作用下转子系统弯扭耦合振动微分方程组为

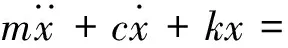
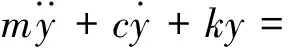
Θμb[kr(u-δ)+α(u-δ)2]R(7)

2 转子弯曲振动和扭转振动特性分析

利用四阶Runge Kutta法，对式(7)进行数值分析，得到系统在不同转速下的振动响应特性。为了避免在数值求解中出现不稳定和漏解等问题，本文是通过应用延拓法来扩大收敛范围。以系统静态平衡向量为初值，应用延拓法对初值进行修正，并以修正后的向量为计算最低转速工况下的初值。此后，随着转速的逐渐增加，各工况下的计算初值为上一工况下的稳态响应向量。转子系统主要参数为：m=213 kg,R=0.4 m,J=10 kg·m2,k=75 880 N/m,kt=47 768 N·m/rad,kr=2.5×107N/m,α=2.5×108N/m2,δ=1e-3m,e=1e-3m,ξ=0.04,ξt=0.02,静摩擦因数μs=0.475，库伦摩擦因数μc=0.075,衰减系数λ=0.55，则扭转振动固有频率ωt0=11 Hz。计算中每一周期积分步长为1/1 000，共计算1 000个周期，舍弃前800个周期，取其后200个周期用来分析。

2.1 转子系统振动特性分析

图2为转子系统弯曲方向响应的分叉图和三维谱图，它们描述了系统随转速变化弯曲振动特性的变化。从图中可以看出转子系统随着转速的升高出现了准周期、周期、倍周期和混沌等丰富地非线性动力学现象。

当转频ω≤1 Hz时，在三维谱图中出现的频率成分以扭转振动固有频率11 Hz及倍频成分为主，频率成分的幅值随着转频的增大而逐渐增大，由分叉图知系统弯曲振动出现非周期运动，这些现象在转频大于1 Hz时突然消失且振动幅值大幅减小。由图3(a)可知，在转频为0.4 Hz工况下，轴心轨迹的半径一直大于转子轴承间间隙因此转子系统做全周碰摩运动，Poincaré截面图呈现为一封闭曲线则转子系统做准周期运动。当转频1<ω<11.6 Hz时，在三维谱图上显示的频率成分以转频为主且随转速的上升逐渐变大，由分叉图可知系统弯曲振动为周期运动。在图3(b)中描述了系统在转频为4 Hz工况下弯曲方向的响应特性，轴心轨迹的半径一直大于转子轴承间间隙因此转子系统做全周碰摩运动，Poincaré截面图呈现为一点则转子系统做周期运动。当转频ω≥11.6 Hz时，在三维谱图上显示的频率成分以转频及其倍频为主且随转速的上升逐渐变大，由分叉图知系统弯曲振动的周期运动已经失稳。由图3(c)可知，在转频为14 Hz工况下，轴心轨迹非常杂乱且运动半径并非总大于转子与轴承间的间隙，因此转子系统做局部碰摩运动，Poincaré截面图中的点杂乱说明转子系统已经处于混沌状态。

图2 转子系统弯曲方向动力学特性

图4为转子系统扭转方向响应的分叉图和三维谱图，它们描述了系统随旋转速度变化扭转振动特性和幅频特性的变化。从图中可以看出转子系统的扭转振动随着转速的升高同样出现了准周期、周期、倍周期和混沌等丰富地非线性动力学现象。

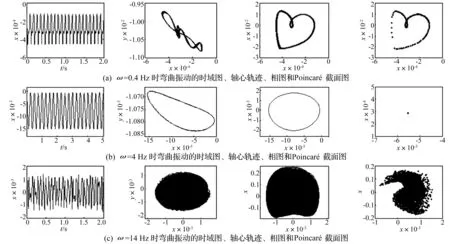
图3 转子系统在不同转频下弯曲振动的时域图、轴心轨迹、相图和Poincaré截面图

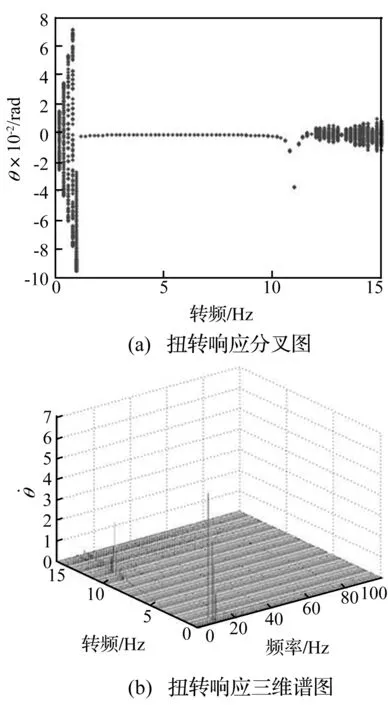
图4 转子系统扭转方向动力学特性

当转频ω≤11.6 Hz时，在三维谱图上中出现的频率成分以扭转振动固有频率 为主，且其幅值随着转频的增大而逐渐增大，由分叉图知系统扭转响应为非周期运动，这些现象在转频大于1 Hz时突然消失且振动幅值也大幅减小。由图5(a)可知，在转频为0.4 Hz工况下，在扭转振动的相图中呈现明显的stick-slip现象，这是由于摩擦力矩的速度依赖特性诱导系统扭转方向的自激振动，且系统通过弯扭耦合作用也将激起弯曲方向的振动。当转频1<ω<11.6 Hz时，在三维谱图上显示的频率成分以转频为主，随转速的上升逐渐变大并在11 Hz转频工况下达到最大值，而后随着转速的上升逐渐减小，由分叉图知系统弯曲振动为周期运动。由图5(b)可知，在转频为4 Hz工况下，扭转的相图为一椭圆而不再有stick-slip现象，这是由于摩擦力矩速度依赖特性产生的负阻尼小于转子系统扭转方向的阻尼，系统将不会出现自激振动，Poincaré截面图呈现为一点则转子系统做周期运动。当转频ω≥11.6 Hz时，在扭转响应三维谱图上显示频率成分以转频和扭转固有频率成分为主，由分叉图知系统扭转振动的周期运动已经失稳。由图5(c)可知，在转频为14 Hz工况下，扭转振动的相图轨迹无序和Poincaré截面图中的点杂乱说明转子系统已经处于混沌状态。

2.2 横向弯曲阻尼比对转子系统响应影响

由于阻尼的存在，转子系统是一能量耗散系统，可以抑制振动幅值的增大。现在将转子系统的横向阻尼比由ξ=0.02增大到ξ=0.1后，以旋转频率作为控制变量转子系统各方向上的分叉图和瀑布图将如图6和图7所示。

图5 转子系统在不同转频下扭转振动的时域图、相图和Poincaré截面图

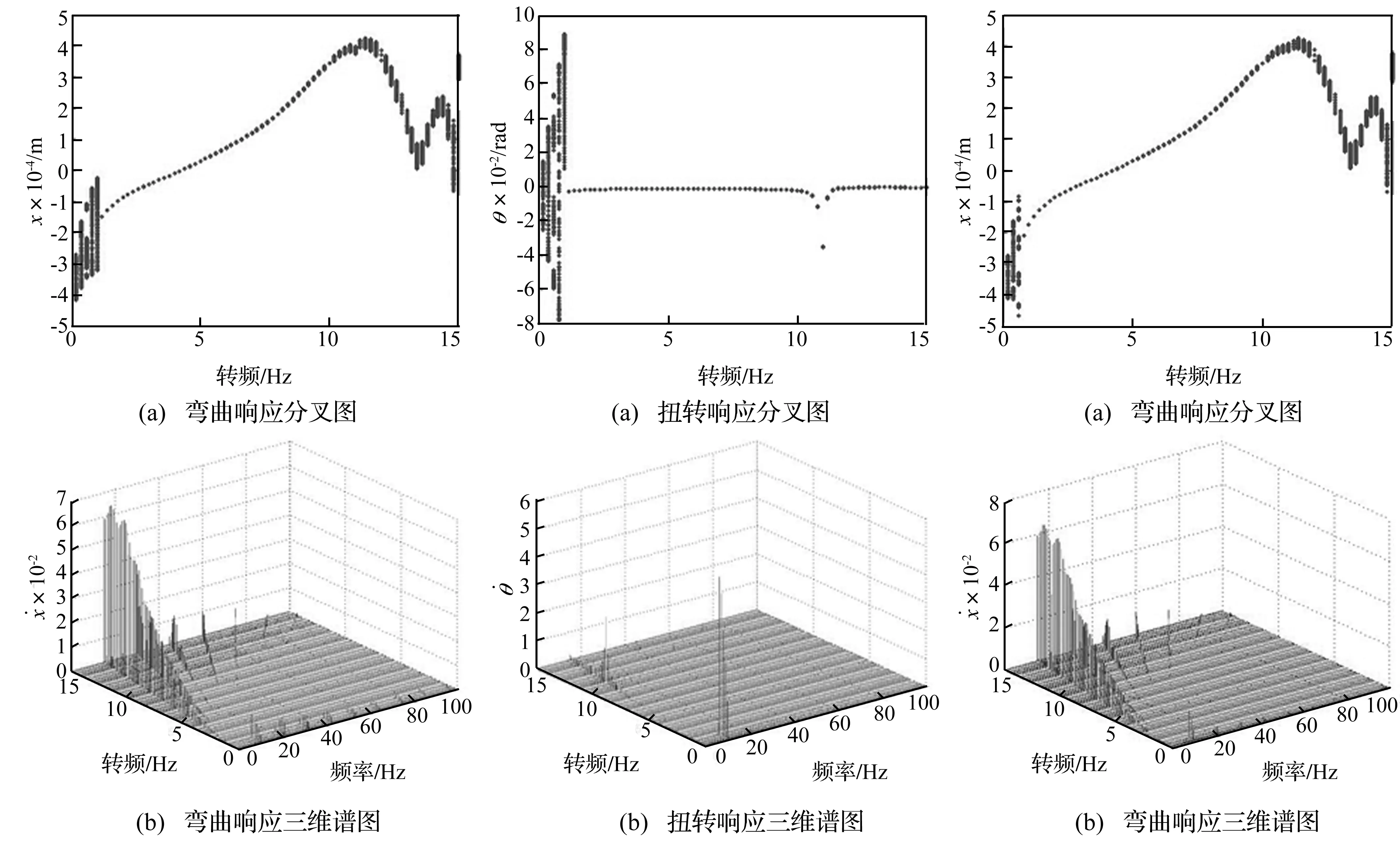
图6 转子系统弯曲方向动力学特性

将图2、4与图6、7进行对比可以发现，由于横向阻尼比的增大，转轴系统自激振动的转速范围并没有发生明显变化但是振动幅值减小了，系统周期运动失稳的转速变大了且在较高转速下系统的横向弯曲响应幅值变小，分叉图中的不动点也较规律了。扭转方向的振动特性并没有由于横向阻尼的增大而有明显的变化。说明横向阻尼的变化对转轴系统在低转速条件下自激振动形成的条件和扭转振动特性影响都很小，而对转轴系统横向振动特性影响较大。

2.3 扭转阻尼比对转子响应的影响

从上面的分析中发现横向阻尼比的变化对自激振动形成条件没有影响，现在分析扭转阻尼比对转子系统振动特性的影响。若在横向阻尼比为ξ=0.1条件下将转子系统的扭转阻尼比由ξt=0.01增大到ξt=0.02后，转子系统各方向上的分叉图和瀑布图将如图8和图9所示。

由图8～图9可知，在旋转频率ω≤0.6 Hz情况下，由于摩擦力矩的速度依赖特性诱导系统扭转产生自激振动，且系统通过弯扭耦合而激起弯曲方向的振动。转子系统在弯曲和扭转方向的振动幅值随着转频的增大而逐渐增大，并在ω>0.6 Hz转频后，系统响应的幅值突然减小并以周期运动形式存在。随着旋转频率的继续增大，扭转振动幅值先增大而后减小并在扭转方向的固有频率 11 Hz有最大值；而横向振动幅值不断增大并逐渐变得不稳定。通过与图6和图7对比发现，由于扭转阻尼比的增大，转子系统自激振动的转速范围和振动幅值均有减小，但是系统周期运动失稳转速并没有发生明显变化。说明扭转阻尼比是影响转子系统在低转速条件下形成自激振动和扭转振动幅值的一个重要系统参数，但是扭转阻尼比的变化对转子系统横向弯曲振动较高转频下的响应特性影响较小。

若将转子系统的扭转阻尼比继续增大，当ξ=0.05时，转子系统各方向上的分叉图和瀑布图如图10和图11所示。

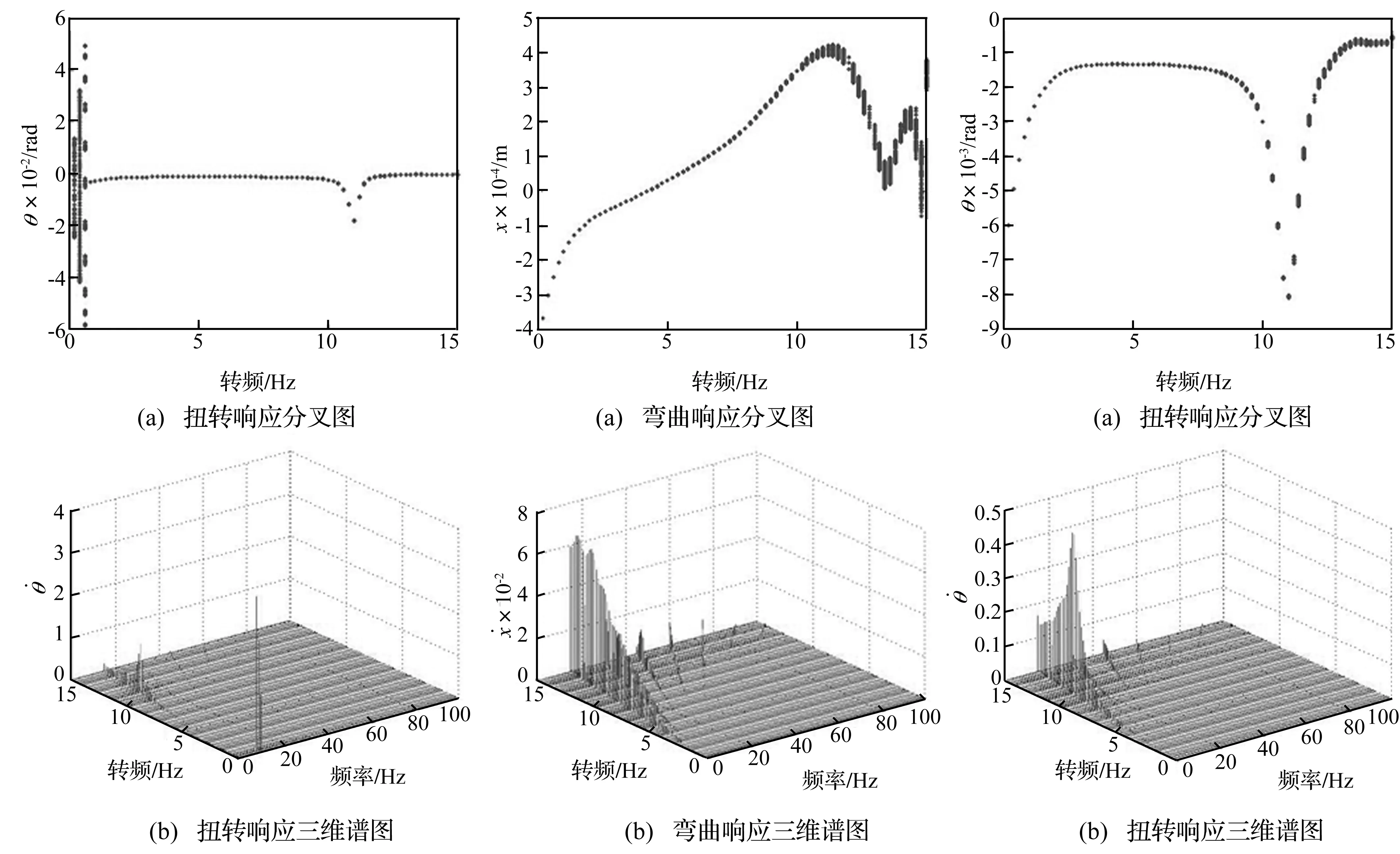
图9 转子系统扭转方向动力学特性

由图10和图11可知，转子系统在低转速条件下并没有发生自激振动，系统弯曲和扭转方向响应均以旋转频率做周期运动。随着旋转频率的增大，扭转振动幅值先增大而后减小并在扭转方向的固有频率 有最大值；而横向振动幅值不断增大并逐渐变得不稳定，转子系统转频的倍频出现并逐渐增大。通过与图6～9进行对比可以发现，由于扭转阻尼比的增大，转子系统自激振动的转速范围减小。当由于速度变化引起扭转方向负阻尼的模小于扭转阻尼时，系统将不会出现自激振动现象。

3 结 论

本文以单盘转子系统为研究对象，考虑橡胶轴承的非线性以及摩擦力的速度依赖性，建立了不平衡转子系统弯扭耦合非线性动力学微分方程，应用数值方法分析了在摩擦力作用下系统的弯扭耦合振动特性。通过对弯曲和扭转方向响应的三维谱图、分叉图、时域图、轴心轨迹、相图以及Poincaré截面图进行分析可以到出如下结论：

(1) 在小阻尼、低转速和共振转速附近条件下，弯扭耦合作用较大。弯扭耦合作用使得弯曲和扭转方向上的激励力相互作用和影响，使得转子系统响应更加复杂。

(2) 在低转频的工况下，由于摩擦力的速度依赖性诱导转子系统扭转方向的自激振动现象，激起扭转方向的固有频率。通过弯扭耦合的作用，转子系统弯曲振动的响应以扭转固有频率及倍频成分为主。在某一转频后自激振动突然消失并引起系统的响应幅值突然大幅度减小。此后，随着转频继续上升，弯曲和扭转的响应幅值逐渐增大，扭转振动在转频等于其固有频率附近产生共振。弯曲振动在某转频后全周碰摩失稳而出现局部碰摩运动，系统响应变得复杂，轴心轨迹杂乱，倍频分量也较大。

(3) 阻尼比系数是影响转子动态响应特性一个重要系统参数。增大横向弯曲阻尼比可以加强转子系统周期运动的稳定性；增大扭转阻尼比可以有效控制转子系统产生自激振动现象的转速范围和扭转振动幅值。

[1] Ehrich F F. High order sub-harmonic response of high speed rotors in bearing clearance[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110: 9-16.

[2] 褚福磊, 张正松, 冯冠平. 碰摩转子系统的混沌特性[J]. 清华大学学报( 自然科学版), 1996, 36(7):52-57.

CHU Fu-lei,ZHANG Zheng-song,FENG Guan-ping. Chaotic behavior of a rub rotor model [J]. Journal of Tsinghua University (Sci & Tech),1996, 3(7): 52-57.

[3] Shang Zhi-yong, Jiang Jun, Hong Ling. The global responses characteristics of a rotor/stator rubbing system with dry friction effects [J]. Journal of Sound and Vibration, 2011, 330: 2150-2160.

[4] Zhang Hua-biao, Chen Yu-shu, Li Jun. Bifurcation on synchronous full annular rub of rigid-rotor elastic-support system [J]. Applied mathematics and mechanics, 2012, 33(7): 865-880.

[5] 花纯利,塔娜,饶柱石. 橡胶轴承-转轴系统碰摩响应动力学特性研究[J]. 振动与冲击, 2014, 33(2): 26-30.

HUA Chun-li, TA Na, RAO Zhu-shi. Dynamic characteristics analysis of a rub-impact rubber bearing-shaft system[J]. Journal of Vibration and Shock, 2014, 33(2): 26-30.

[6] Tondl A. Some problems of rotor dynamics [M]. London, Chapman and Hall, 1965.

[7] Kato M, Ota H, Nakamura S I. Torsional vibration of a rotating rotor driven by constant acceleration[A]. Kitakyushu, 1993.

[8] 刘占生,崔颖,黄文虎,等. 转子弯扭耦合振动非线性动力学特性研究[J]. 中国机械工程, 2003, 14(7):603-605.

LIU Zhan-sheng, CUI Ying, HUANG Wen-hu, et al. Study on nonlinear dynamics characteristics of a rotor with coupled bending and torsional vibrations[J]. China Mechanical Engineering, 2003, 14(7): 603-605.

[9] Al-Bedoor B O. Transient torsional and lateral vibration of unbalanced rotors with rotor-to-stator rubbing [J]. Journal of Sound and Vibration, 2000, 229:627-645.

[10] Yuan Zhen-wei, Chu Fu-lei, Hao Ru-jiang. Simulation of rotor’s axial rub-impact in full degrees of freedom[J]. Mechanism and Mechine Theory, 2007, 42 (7): 763-775.

[11] Patel T H, Darpe A K. Coupled bending-torsional vibration analysis of rotor with rub and crack [J]. Journal of Sound and Vibration, 2009, 326 : 740-752.

[12] 韩放, 郭杏林, 高海洋. 非线性油膜力作用下叶片-转子-轴承系统弯扭耦合振动特性分析[J].工程力学, 2013, 30(4): 355-359.

HAN Fang, GUO Xing-lin, GAO Hai-yang. Research on coupled bending and torsion vibration of blade-rotor-bearing system with nonlinear oil-film force[J]. Engineering Mechanies, 2013, 30(4):355-359.