含时变刚度及侧隙的多级齿轮系统非线性动力学特性分析

胡 鹏, 路金昌, 张义民

(东北大学 机械工程与自动化学院，沈阳 110819)

多级齿轮传动系统被广泛的应用于机械工业领域，机床刀架的动力就是通过齿轮传动实现的。保证动力系统传动的平稳性，降低振动和噪音是动力分析的基本任务之一。李润方等[1]对齿轮传动系统的建模方法，模型的类型以及非线性因素等多方面作了深入研究。对于单对齿轮的动态特性，Kahraman等[2-3]给出了基于实验的非线性动力学模型，考虑内部激励和外部激励，从数值和解析两方面给出动态响应分析。 唐进元等[4]研究了间隙对含摩擦和时变啮合刚度的动力系统动力学的影响。高建平等[5]对4自由度直齿轮非线性方程组采用基于打靶法的局部参数延拓法进行了数值求解。Lin[6]对单级直齿轮系统的相关参数进行了详细研究，并给出参数值变动对动态响应的影响。李发家等[7]采用集中质量法，建立了行星齿轮传动系统的非线性动力学方程，采用Runge-Kutta法求解了系统的响应。多级齿轮传动系统的研究相对受限，许多对系统影响显著的复杂因素，例如元件之间的相互耦合，轴承的支撑作用，脱齿以及滑动摩擦，没有完全加入模型当中。唐增宝等[8]考虑时变啮合刚度的影响，提出了多级齿轮传动动态仿真技术，采用模态分析法和状态空间相结合的方法进行求解。Al-shyyab A等[9]对非线性多级齿轮采用谐波平衡法进行了解析求解，并分析了其动态响应特性。Lin等[10]对含时变刚度，脱齿现象的中间轴齿轮系统和惰轮齿轮系统的非线性动力学进行了深入研究，采用摄动法进行了解析求解，并与数值解比较。Raclot[11]介绍了一个考虑形状偏差和安装误差对动力学行为影响的数学模型，包括单齿对和多级传动模型。Liu[12]研究了多级齿轮系统的非线性问题，给出3个数学模型，采用数值法和近似解析法进行了求解，并与有限元基准模型进行了对比，研究了参数不稳定性，脱齿以及齿廓修形等问题。

在上述文献的基础上，本文考虑时变啮合刚度，齿轮静态传递误差，齿侧间隙等因素的影响，建立了动力伺服刀架多级齿轮传动系统的扭振模型，采用Runge-Kutta法对系统进行动力学数值求解，并对仿真结果进行分析。通过改变转速，啮合刚度以及齿侧间隙的大小，研究相应参数对动力学响应的影响，为改善系统的传动平稳性，降低噪音提供理论依据。

1 多级齿轮传动系统扭转振动模型

多级齿轮系统的非线性分析较为复杂，为了简化分析，本文模型只考虑扭转振动，同时满足以下假设：

(1) 电机连接轴和输出轴的扭转刚度远小于弯曲刚度，进而认为两齿轮的中心固定，只做扭转运动；

(2) 忽略所有轴承和中间惰轮轴的弹性变形；

(3) 忽略轮齿之间的摩擦力；

(4) 啮合的两齿轮均为渐开线直齿圆柱齿轮，啮合力始终作用在啮合线方向上，两齿轮简化为由阻尼和弹簧相连接的圆柱体。

1.1 模型的简化

图1为四级直齿圆柱齿轮传动系统，系统的模型是在齿轮副纯扭转的基础上考虑了传动轴的扭转刚度和电动机和负载的转动惯量。为了便于模型的建立和求解，把轴的转动惯量按功能等效和质心不变原理分配到各轴的齿轮或转子上，即将轴转变为弹簧阻尼元件，经换算后的系统动力学模型如图2所示。

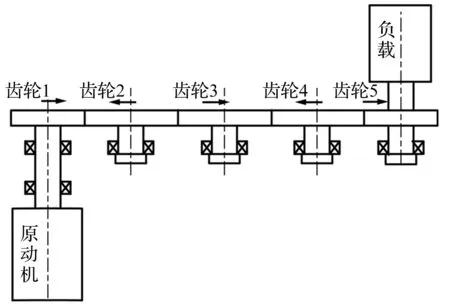
图1 四级直齿圆柱齿轮传动系统

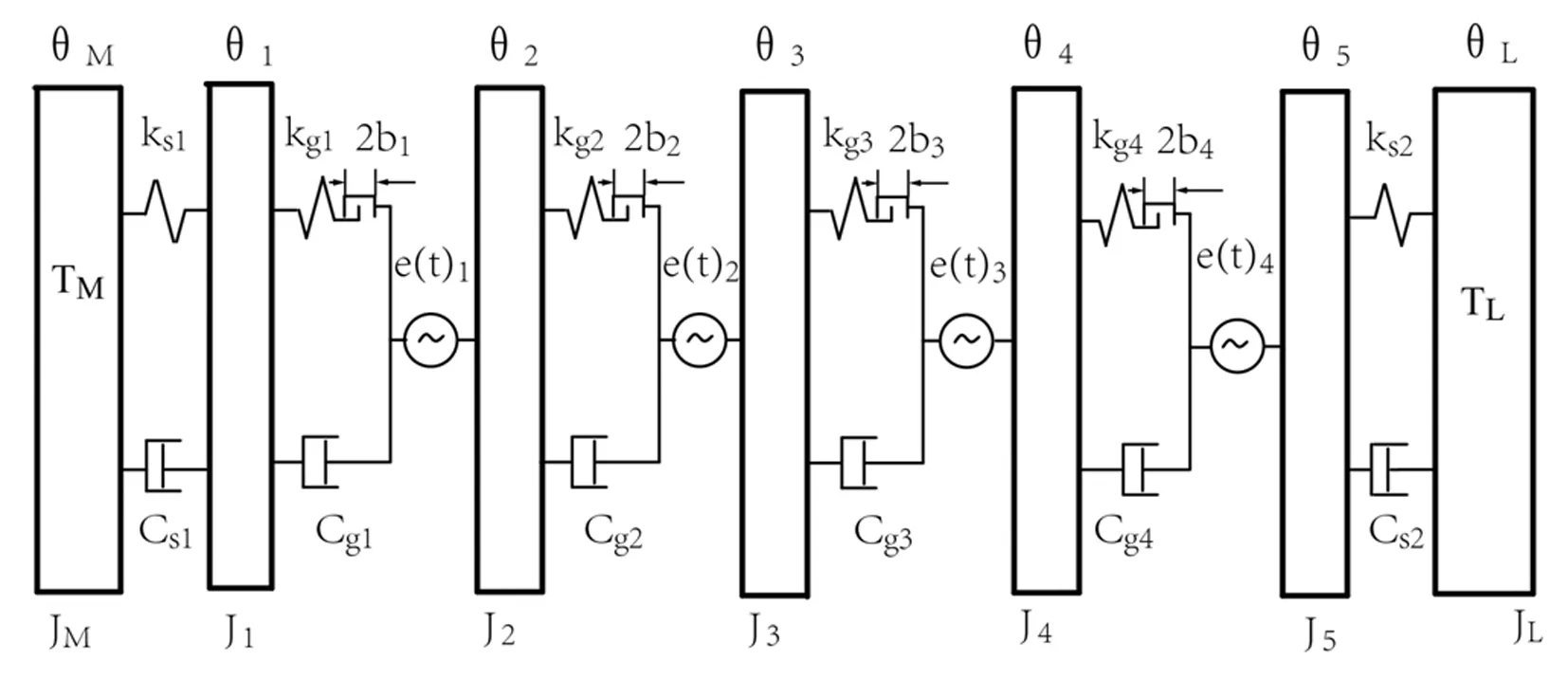
图2 四级直齿圆柱齿轮传动系统动力学模型

在图2中，θM，θ1，θ2，θ3，θ4，θ5，θL分别表示电动机、齿轮和负载的角位移；JM，J1，J2，J3，J4，J5，JL为质量元件的转动惯量；Cs1和Cs2为轴的扭转阻尼；ks1和ks2为轴的扭转刚度；kg1，kg2，kg3和kg4为各级齿轮副的时变啮合刚度；Cg1，Cg2，Cg3和Cg4为各级齿轮副的啮合阻尼；b1，b2，b3和b4为啮合齿对的半侧隙；TM和TL为电动机和负载上的扭矩。

1.2 非线性动力学微分方程的建立

基于给定的假设条件，得到四级齿轮传动系统7自由度动力学微分方程。

(1)

式中，Rbi为各齿轮的基圆半径，Wdi为齿轮动态啮合力，且

其中，e1(t)，e2(t)，e3(t)，e4(t)为啮合齿轮副的静态传递误差。令uj=Rbjθj(j=1,2,3,4,5)，则动态传递误差xi(t)=(ui-ui+1)。gi(t)(i=1,2,3,4)为分段函数，其数学表达式如下：

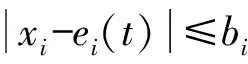
对于纯扭转模型来说，其矩阵形式可以表示如下

(2)

式中，U为等效位移向量，设uM=Rb1θM，uL=Rb5θL；M为质量矩阵，C为阻尼矩阵，K为包含时变啮合刚度的矩阵，FT为外部载荷向量。E为由啮合阻尼、时变啮合刚度和静态传递误差引起的激励向量，令δi∈{ei(t)-bi,0,ei(t)+bi}，它的取值与上述分段函数的判定条件相对应。则

U=[uM,u1,u2,u3,u4,u5,uL]T

FT=[TM/Rb1, 0, 0, 0, 0, 0, -TL/Rb5]T

2 模型中参数的计算

啮合过程中的啮合刚度kg具有明显的周期性，在单双齿交替啮合时有突变。为简化计算，齿轮啮合刚度的周期性变化可等效为图3所示的矩形波形式。

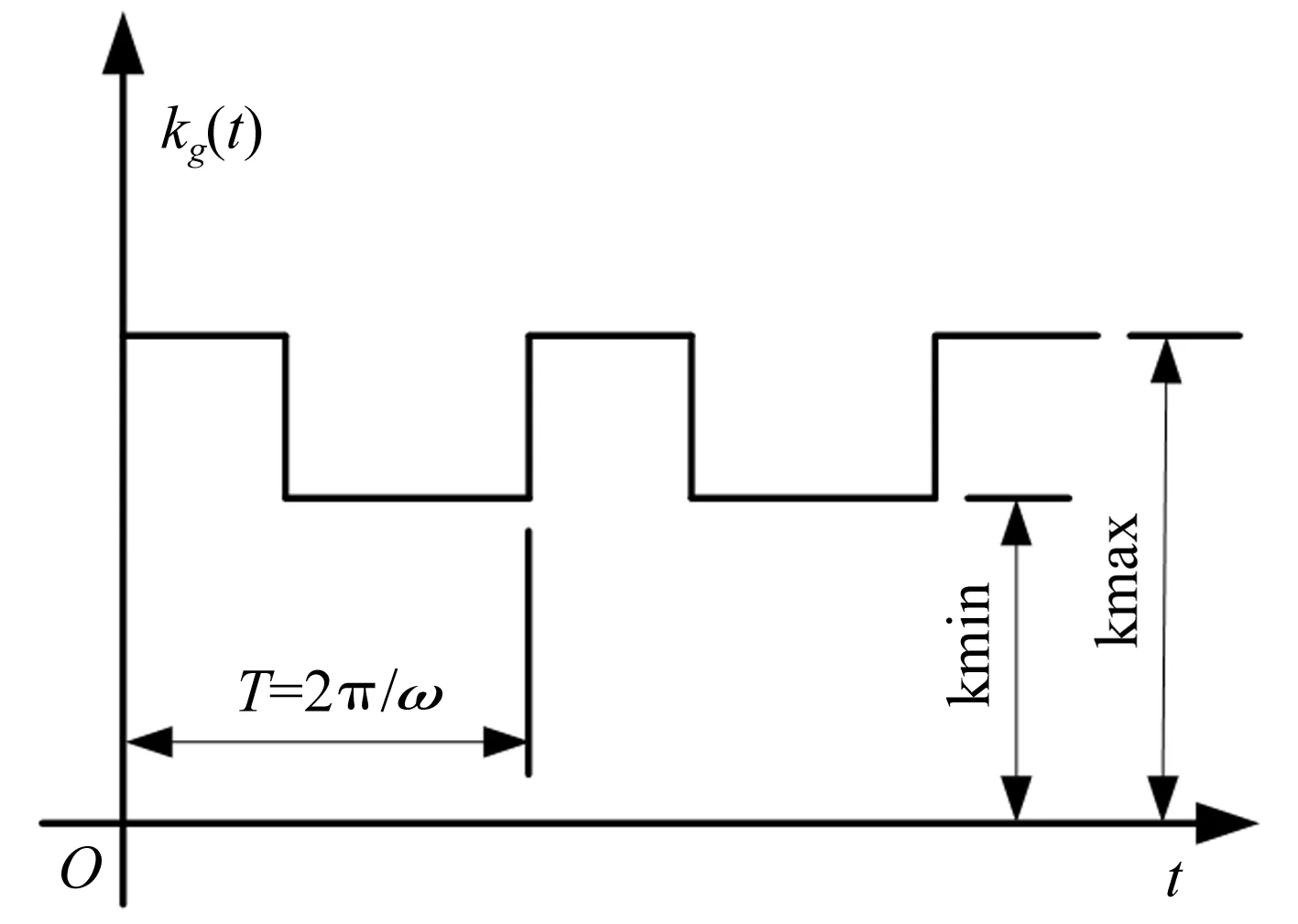
图3 简化的啮合刚度周期变化

函数表达式如下：

(3)

式中，kmax和kmin分别取双齿啮合和单齿啮合时的平均值，T为啮合周期，ε为重合度。

将式(3)所示的啮合刚度以啮合频率进行傅里叶级数展开，取一阶分量进行计算，则

kg(t)=km+amcos(ωmt)+bmsin(ωmt)

(4)

式中，km，am，bm分别为傅里叶展开式的常数项，一阶余弦项和正弦项，且

km=(ε-1)kmax+(2-ε)kmin

am=(kmax-kmin)sin(2πε)/π

bm=-[kmin+(kmax-kmin)cos(2πε)]/π

参数ωm为齿轮副的啮合频率：

ωm=2πn1z1/60

静态传递误差e(t)是由齿形误差，齿距偏差和齿的弹性变形等因素组成的周期性位移激励，以内部激励的基频进行傅里叶级数展开，同样保留一阶项

e(t)=e0+Aesin(ωet+φ)

(5)

式中，e0为常数项，Ae为一阶谐波幅值，φ为相位角，ωe=ωm。

阻尼效应的数学描述是十分复杂的，为了便于振动响应分析，采用以下公式进行简化求解

式中，kg取啮合刚度的均值，ξg为轮齿啮合的阻尼比，按照Kasuba[13]和Wang[14]的分析计算，一般取值为0.03～0.17，此处取均值0.1。

传动轴的扭转刚度的计算表达式为

ks=IpG/ls

式中，Ip为极惯性矩，G为剪切模量，ls为轴长。

电动机连接轴和负载连接轴的阻尼表达式为

式中，ξs为轴的阻尼比，根据文献[15]的实验结果，ξs为0.005～0.007，本文取0.005。

3 动态仿真结果分析

以图1所示的传动系统为例进行仿真，给定齿轮基本参数，精度等级均为5级。电动机转子的转动惯量为0.006 15 kg·m2，转速为4 000 r/min；输入输出轴的长度分别为80 mm，33.7 mm，内外径分别为d1out=58 mm，d1in=38 mm，d2out=36 mm,d2in=25 mm；各齿对半齿侧间隙b取50 μm，电动机转矩TM=35 N·m，负载力矩为TL=54 N·m。

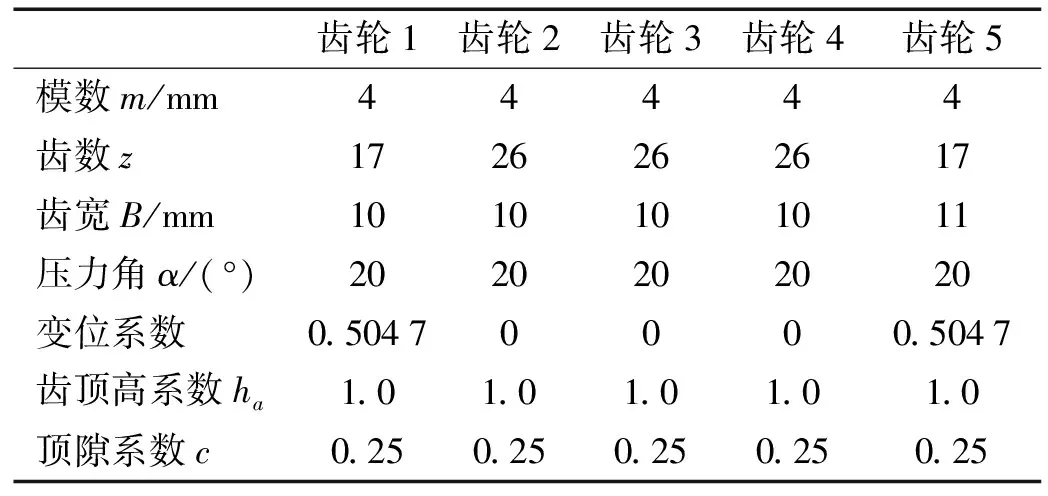
表1 传动系统齿轮的基本参数

3.1 啮合刚度的求解

根据文献[16]，结合表1中的参数，采用MATLAB和ANSYS的APDL语言编程计算，结果如图4所示，kg表示的是单位齿宽上的刚度大小。由于齿对2和3参数一致，其计算结果相同。以齿对1为例，由文献[17]可知，基于石川公式的日本机械学会的结果为17.2 N/(mm·μm)；基于威伯-班纳斯切克公式的ISO公式草案的近似值为18.91 N/(mm·μm)；ANSYS计算结果的平均值为18.74 N/(mm·μm)；本文采用文献[16]算法求出的平均值为19.78 N/(mm·μm)。计算误差分别为13.04%，4.4%和5.26%，由于石川公式将轮齿看做一个梯形加上矩形的组合，其齿厚较精确建模要小，变形量偏大，所以刚度值偏小，误差较大。

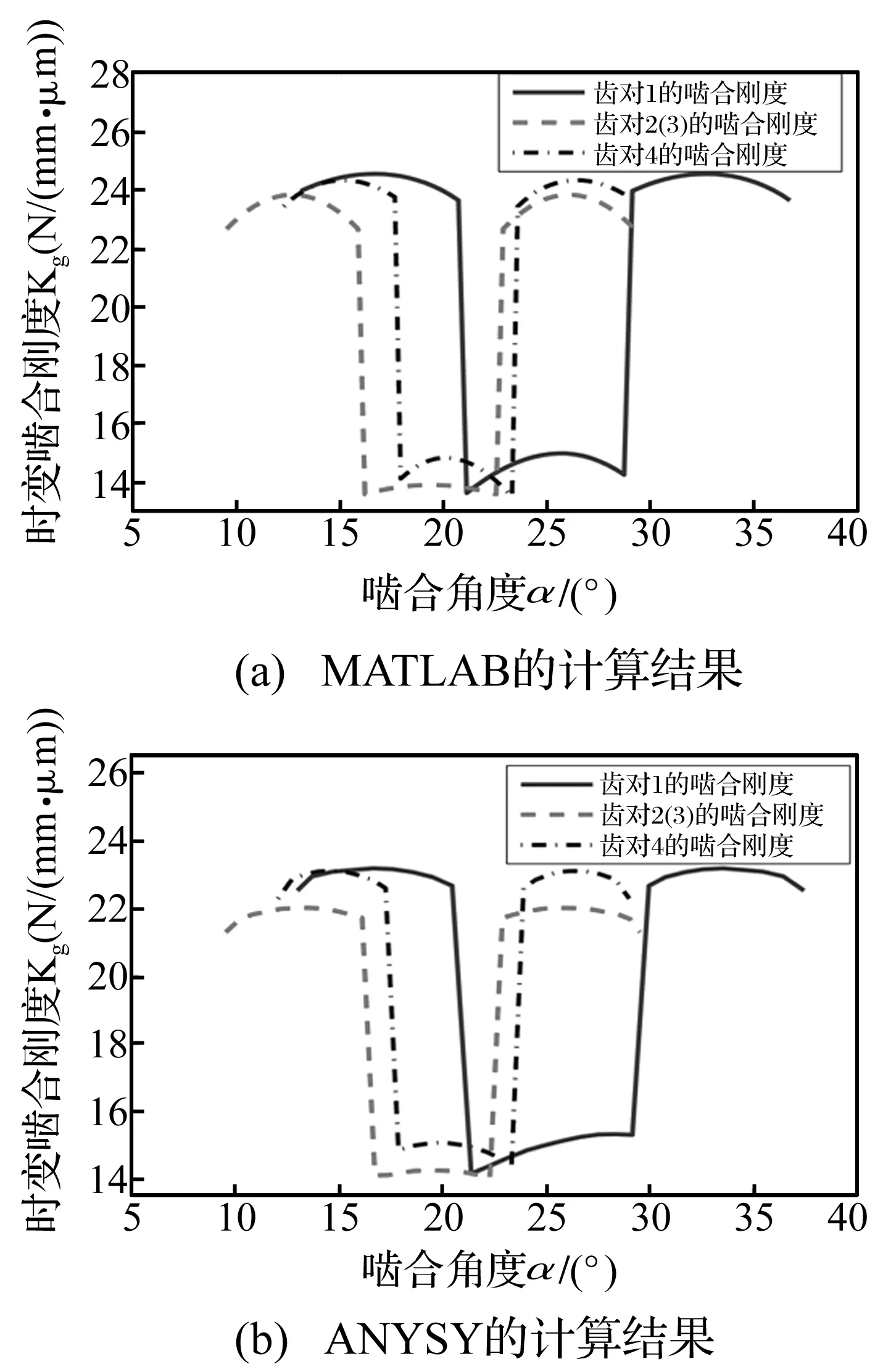
图4 各级齿对的啮合刚度值

结合公式(3)和(4)，得到各齿对啮合刚度的展开项值，其结果由表2给出。

3.2 动态传递误差

对方程式(2)采用四阶Runge-Kutta法进行求解，得到动态响应结果。动态传递误差(DTE)的时域图和频谱图如图5和图6所示，分别对应输入端和输出端齿对的响应情况。由图5知，齿对1的DTE的均值比齿对4的值要小，这是由于齿对1的啮合刚度要比齿对4的值大，啮合变形量较小，故其DTE的均值相对较小。

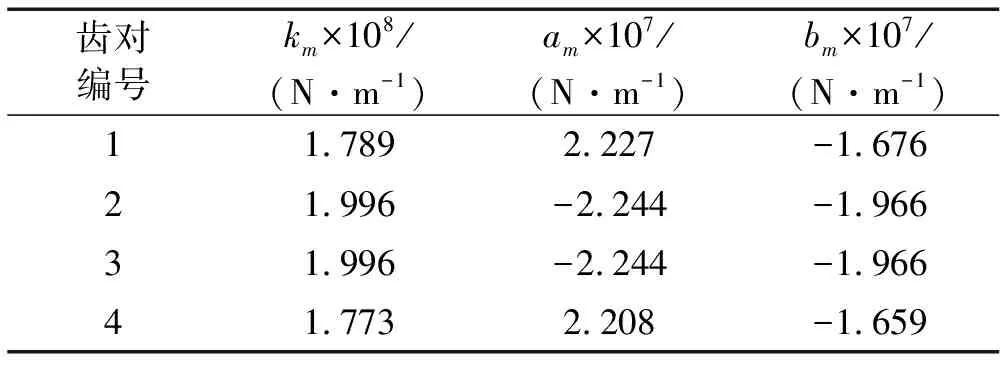
表2 各级啮合刚度的展开项数值

从频谱图6中分析，齿对1与齿对4的主要幅值的频率点是一致的，对应频率值有497，636，1 133，1 630，2 266，3 399 Hz等，由系统的固有特性分析可知，497 Hz为系统的二阶固有频率f2，1 133 Hz对应系统的啮合频率fn；而fn-f2和fn+f2对应636 Hz和1 630 Hz，2 266 Hz，3 399 Hz为二倍啮频和三倍啮频，且齿对4在二倍啮频处幅值较齿对1的大。由于其响应结果中含有值为半侧隙b的常值项，所以在0 Hz处存在较大振幅，为了体现其他频率下较小的幅值情况，在图中没有体现。

啮合刚度值影响着DTE的大小，转速同样对DTE值有较大影响，而DTE是影响齿轮系统平稳性的主要因素，所以给出不同啮合刚度在不同转速下的DTE的均方根幅值(减去均值后)(Root-mean-square, RMS)和均值。设定各级啮合刚度值分别取0.9 kg，kg，1.1 kg和1.2 kg，转速变化范围设为1 000～10 000 r/min，结果如图7和图8所示；由于不同啮合刚度下DTE变化趋势大体一致，图9只给出了啮合刚度为kg时啮合过程中出现的三种啮合状态的比例值。

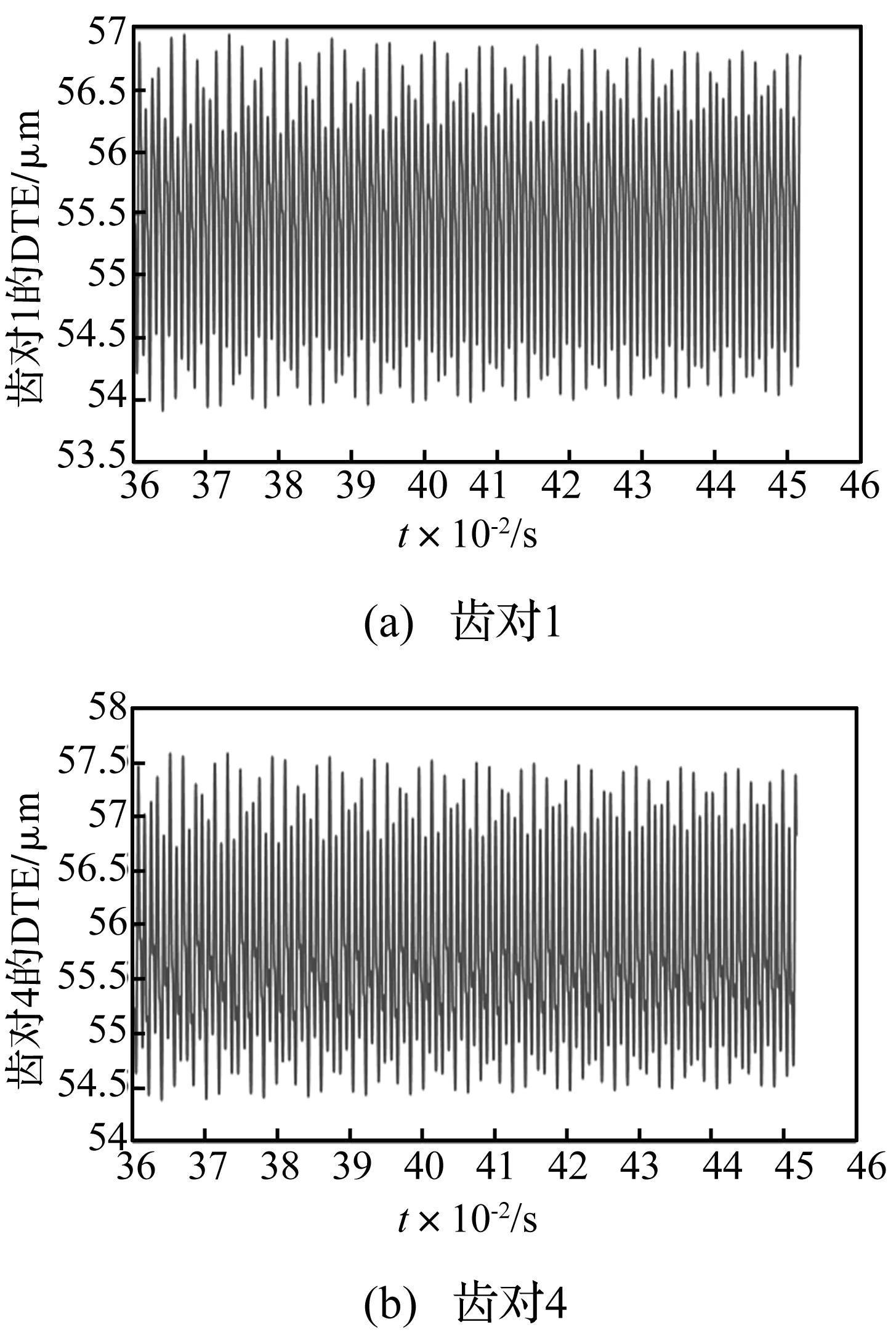
图5 齿对1和4的DTE时域图，n=4 000 r/min

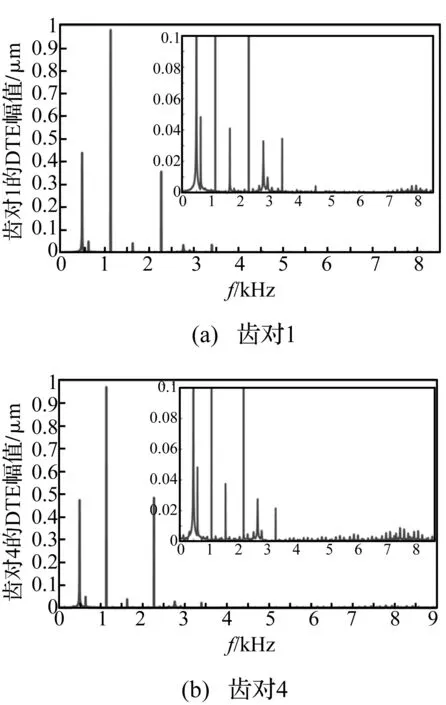
图6 齿对1和4的DTE频谱图，n=4 000 r/min

由图7知，不同啮合刚度下，齿对1和4的DTE的均方根值在低速段和高速段存在较大波动，这是由于系统的强非线性而出现的混沌现象，而转速在4 000～8 000 r/min 时，齿对的DTE幅值较小，由图6的频谱图可以看出，系统处于准周期啮合状态。图8为齿对的DTE的平均幅值，由于齿侧间隙的存在，导致啮合状态发生改变，出现较大比例的啮合脱齿和侧面接触，使得均值减小；在平稳波动段，通过局部放大图可以看到啮合刚度越大，其DTE的均值越小，这是由于DTE中含有的啮合变形部分减小。从图9不难看出，啮合状态在4 000～8 000 r/min范围主要为正面啮合，即正常啮合，而在其他段则出现较大比例的脱齿，这导致了图7和图8现象的产生，所以对于非线性系统，要注意其对参数的敏感性，避免产生较大波动的响应结果。

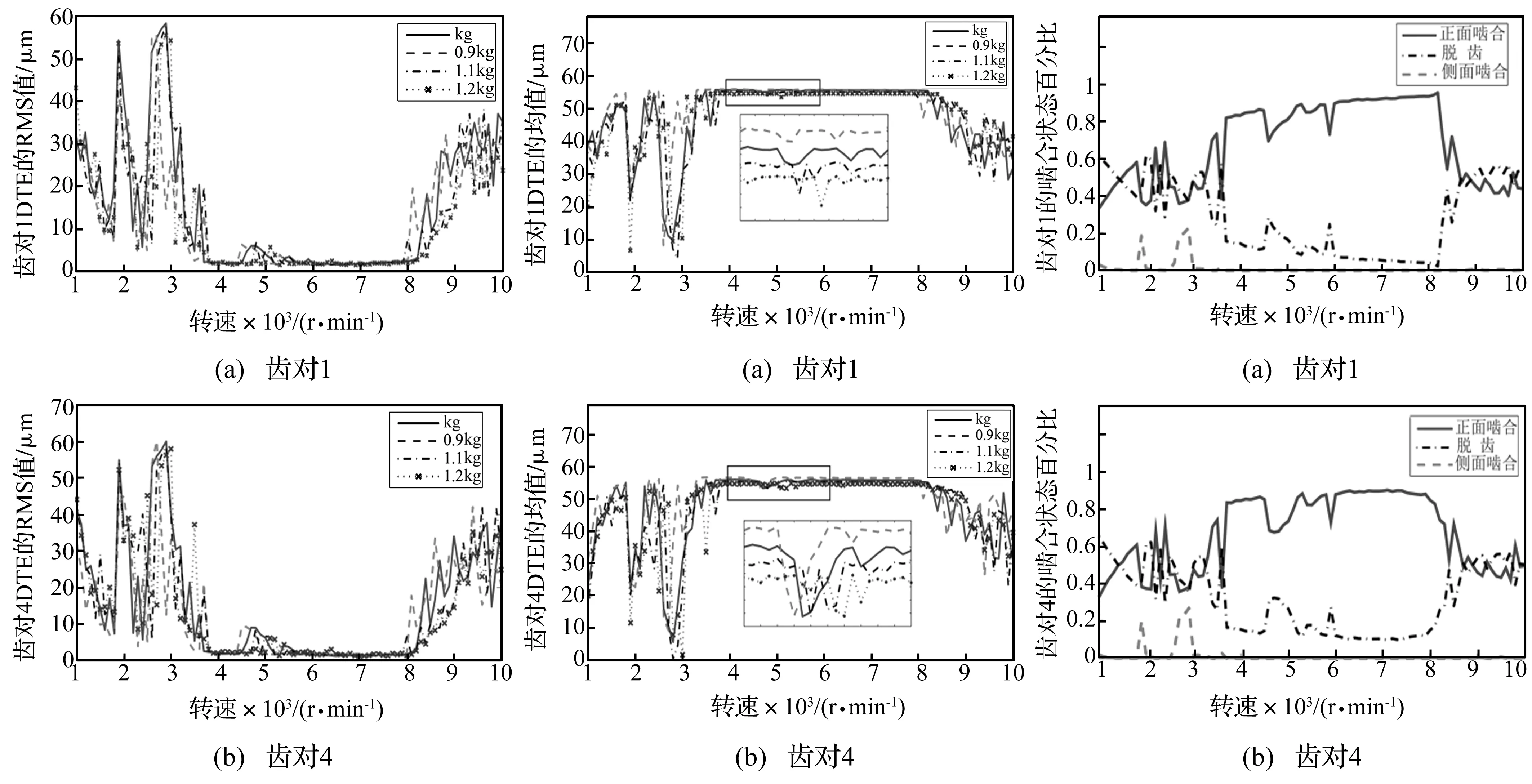
图7 齿对1和齿对4的DTE的RMS(减去均值后)值

3.3 动态啮合力

齿轮系统中的动态啮合力的变化体现了冲击程度并影响系统噪音的大小。图10给出了转速为4 000 r/min时的动态啮合力，由图10(a)可知，齿对1动态啮合力最大可达2.3倍的静态啮合力，且趋于零的值所占比例较小，即脱齿的状态较少，这与图8的结果一致。图10(b)所示齿对4的动态啮合力最大为2.5倍的静态啮合力，其它趋势与齿对1相同。由图7和图8知，转速在1 000～3 000 r/min及8 000～10 000 r/min处幅值有较大波动，图9表明此时出现了较大比例的脱齿，且还有侧面接触，从而导致了幅值的波动。图11为转速是3 000 r/min的动态啮合力，可知啮合过程中零值所占比例增大，偶有负值，与图7～图9的结果吻合。当啮合刚度发生变化时，啮合力的值随啮合刚度的增大而增大，图12为转速4 000 r/min，啮合刚度为1.2kg的仿真结果，比kg的结果稍大，且啮合状态比例中脱齿现象更加明显。

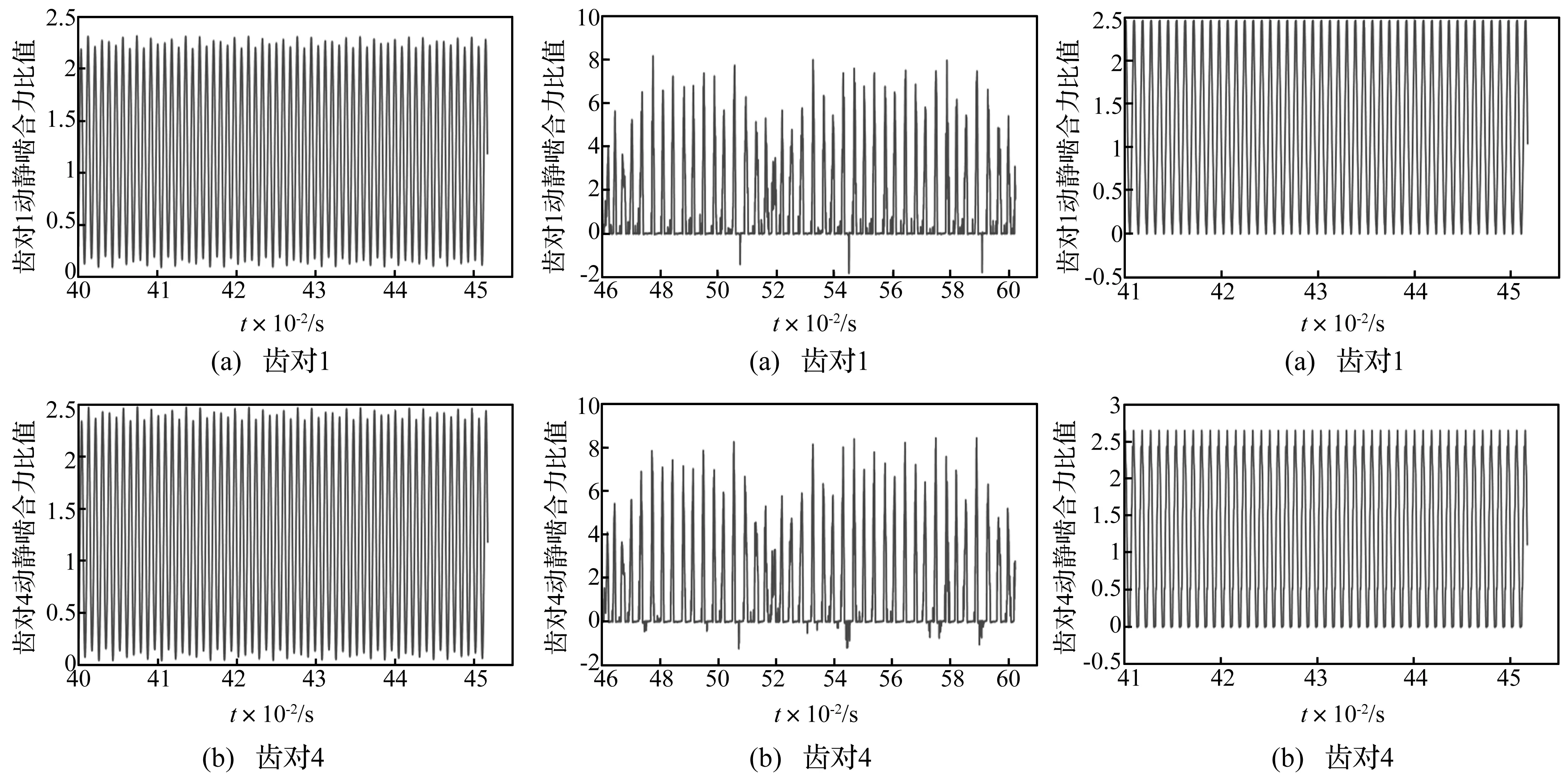
图10 齿对1和齿对4的动静啮合力比值，n=4 000 r/min

4 结 论

(1) 建立了含时变啮合刚度，齿侧间隙和静态传递误差的动力学模型，对模型进行了合理的简化，用数值解法进行了求解。

(2) 在转速为4 000 r/min时，对齿对1和齿对4的DTE进行了时域和频谱分析，可以看出系统处于准周期啮合状态，且波动较为平稳；从频谱图看出，幅值主要处于f2，fn-f2，fn，f2+fn，2fn，3fn等频率点。

(3) 分析了齿对的DTE在不同啮合刚度下随转速变化的均方值(减去均值)和平均值。不同转速段下系统的啮合状态存在较大差异，导致均方差和平均幅值存在较大波动，当啮合状态中脱齿所占比例较大时，系统的响应处于混沌状态，而当其比例较小时系统基本处于准周期状态。

(4) 在分析了DTE的基础上，分析了动态啮合力随转速及啮合刚度变化的影响，其变化情况同样受到啮合状态变化的影响。

[1]李润方，王建军.齿轮系统动力学振动、冲击与噪声[M]. 北京：科学出版社，1997.

[2]Kahraman A, Singh R. Non-Linear Dynamic of a spur gear pair[J]. Journal of Sound and Vibration, 1990,142(1):49-75.

[3]Kahraman A, Singh R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system[J]. Journal of Sound and Vibration, 1991, 146(1):135-156.

[4]陈思雨，唐进元. 间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响[J]. 机械工程学报，2009,45(8):119-124.

CHEN Si-yu, TANG Jin-yuan. Effect of backlash on dynamics of spur gear system with friction and time-varying stiffness[J]. Chinese of Journal of Mechanical Engineering,2009,45(8):119-124.

[5]高建平，方宗德，杨宏斌. 具有时变啮合刚度传动误差及间隙的齿轮系统动力学分析[J]. 航空学报，1999,20(5):440-444.

GAO Jian-ping, FANG Zong-de, YANG Hong-bin. Dynamic analysis of spur gear pairs with time-varying mesh stiffness and clearance non-linearity[J]. Acta Aeronautica et Astronautica Sinica, 1999,20(5):440-444.

[6]Lin H H, Liou Chuen-Huei. A parametric study of spur gear dynamics[R]. NASA of US:Lewis Research Center,1998.

[7]李发家，朱如鹏，鲍和云，等.行星齿轮系动力学特性分析及试验研究[J]. 南京航空航天大学学报，2012,44(4):511-518.

LI Fa-jia, ZHU Ru-peng, BAO He-yun, et al. Dynamics characteristic and experiment research on planetary gear system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4):511-518.

[8]唐增宝，钟毅芳，刘伟忠.多级齿轮系统的动态仿真[J]. 机械传动,1993,17(1):37-41.

TANG Zeng-bao, ZHONG Yi-fang, LIU Wei-zhong. Dynamic simulation of multi-stage gear transmission system[J]. Journal of Mechanical Transmission,1993,17(1):37-41.

[9]Al-shyyab A, Kahraman A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: period-one motions[J]. Journal of Sound and Vibration, 2005,284:151-172.

[10]Lin J, Parker R G. Mesh stiffness variation instabilities in two-stage gear system[J]. Journal of Vibration and Acoustics,2002,124(1):68-76.

[11]Raclot J P, Velex P. Simulation of the dynamic behaviour of single and multi-stage geared systems with shape deviations and mounting errors by using a spectral method[J]. Journal of Sound and Vibration, 1999,220(5):861-903.

[12]Liu G.Nonlinear dynamics of multi-mesh gear systems[D]. The USA: The Ohio State University,2007.

[13]Kasuba R, Evans J W. An extended model for determining dynamic loads in spur gearing[J]. Journal of Mechanical Design, 1981,103(2):398-409.

[14]Wang K L, Cheng H S. A numerical solution to the dynamic load, film thickness and surface temperature in spur gears[J]. Journal of Mechanical Design, 1981, 103(1):177-187.

[15]Hahn W F. Study of instantaneous load to which gear teeth are subjected[D]. The USA: University of Illinois,1969.

[16]Cornell R W. Compliance and stress sensitivity of spur gear teeth[J]. Journal of Mechanical Design, 1981, 103(2):447-459.

[17]日本机械学会.齿轮强度设计资料[M]. 北京:机械工业出版社，1984:28-35.