基于FFT多谐波平衡法的金属橡胶隔振系统振动特性分析

李玉龙，白鸿柏，何忠波，路纯红，李冬伟

(军械工程学院,石家庄 050003)

近年来，随着科学技术的飞速发展，隔振系统的工作环境日益复杂、恶劣，复杂的工况对隔振系统性能的要求也不断提高，因此，基于干摩擦耗能机理的非线性隔振器如钢丝网隔振器、钢丝绳隔振器、金属橡胶隔振器等获得了较大的发展和应用。以金属橡胶隔振器为例，由于其耐高温、抗腐蚀、隔振频带宽、能够自动避开共振有效的抑制振动幅度等独特的优势，越来越受到工程界的高度重视，在航空航天、尖端军事工业等高科技领域得到了广泛的应用[1]。但它们的广泛应用需要更加精确的方法以准确地计算振动响应，这类振动系统的响应计算也成为了研究的热点问题。

国内外学者对具有干摩擦的振动系统的响应计算做了大量的研究[2-8]。总结来看研究这类问题的方法有拓扑几何法、数值法和解析法。拓扑几何法仅获得非线性振动的定性规律；数值法可以进行定量分析；解析法不仅能确定非线性系统运动随时间变化的规律，而且还能得到运动特性对系统参数的依赖关系，是非线性振动问题研究的重要方法。但大部分非线性动力学问题不存在精确的解析解。目前常用的近似解析法有摄动法、平均法、多尺度法、谐波平衡法等。但它们对系统响应解的形式没有严格的判定依据，大部分学者采用以激励频率为主导的单一谐波平衡法[3,7-8]。但是，非线性系统的振动往往包含多谐波成分[9-10]，单一谐波平衡法却忽略了其他谐波的作用，很难获得与实际响应匹配较好的精确解。文献[9]提出了FFT多谐波平衡法，采用多个谐波作为非线性微分方程的基础解，证明了该方法能较好地适应非线性隔振系统多种频率成分共存的运动响应情况。本文也将基于FFT多谐波平衡法，来研究探讨金属橡胶类非线性迟滞隔振系统的振动响应问题。

1 力学模型

根据应用领域的不同，金属橡胶可以设计成不同结构以制备隔振器，满足不同的隔振需求，军械工程学院白鸿柏教授做了大量的研究，并设计了多种隔振器结构，最常见的结构形式如图1所示。

图1 金属橡胶试件

(1)

一般无记忆恢复力g0是变形状态的二元函数，可展开为多项式形式如下。

(2)

图2 力学模型

尽管无记忆恢复力的一般表达式比较复杂，但是工程中常见的金属橡胶隔振器实验建模结果表明，无记忆恢复力中的立方非线性成分是主要的支配因素。因此它们可以用含有立方非线性粘性阻尼双线性迟滞模型来近似描述，且足以满足工程应用中的精度要求[4]。若以单自由度金属橡胶隔振系统为例，其力学模型如图2所示，设作用于设备的激励是简谐激励：p(t)=p0cos(ωt)。

振动系统的运动微分方程可以写为：

z(t)=p0cos(ωt)

(3)

2 FFT多谐波平衡法

根据谐波平衡的思想，系统中尽管存在非线性因素的影响，但在一定条件下其定常解仍然是近似简谐的[10]，且非线性系统的多谐波振动响应是具有普遍性的现象，因此可以将该非线性振动系统的解表达为具有多谐波的组合形式[9]：

(4)

式中，αm为整数或分数(α1=1)分别代表超谐波和亚谐波运动响应成分；ω为系统的激振频率；A1，…，Am，B1，…，Bm代表谐波分量幅值。

对于孔子已经评价过的人物，司马迁常常是直接采取孔子的评价，例如称吴太伯为“至德”，称微子、箕子、比干为殷之“三仁”，称董狐为“良史”，赵盾为“良大夫”，子产为“古之遗爱”。这些都是孔子已经评价过的人物，司马迁便因袭孔子的观点，直接以孔子的评价作为自己的评价。而对于孔子以后或者孔子所未评论到的人物，司马迁也非常善于使用孔子留下来的概念来进行评价，如评价吕不韦为“闻”，评价万石、建陵、张叔为“君子”，评价田叔“居是国必闻其政”，这都是借用孔子留下的现成概念或标准来评价人物。由此我们可以看出，在评价历史人物时，孔子的评价标准也是司马迁的重要价值尺度，甚至取舍褒贬都与孔子一致。

可将式(4)代入振动微分方程，并化简降阶为关于cos(αmωt),sin(αmωt),(m=1,2,…,M)的方程。由于系统各阶谐波分量保持平衡，相同阶数谐波系数应相等，有如下关于各谐波分量的非线性方程组。

(5)

解方程组(5)可以得到谐波项的系数，进而得到系统的振动响应，显然该方法的精度受到谐波项的数量和频率的影响。

若先用四阶Runge-Kutta法求出系统响应的数值解，再对响应进行快速傅里叶变换(FFT)将信号转化到频域内，提取出主要的频率成分，以确定系统响应中的主要谐波分量信息。这样就可以确定系统响应的精确解析解。这种方法即为FFT多谐波平衡法[9]。

假设由上述方法获得某金属橡胶隔振系统的多谐波解析解，表达式为：

y(t)=y1cos(ω1t+φ1)+…+

ymcos(ωmt+φm)

(6)

由式(6)可得系统振动响应式周期振动，振动周期为：

T=2aπ/ω

(7)

其中，a是系统振动响应所包含的频率成分ω1,ω2,…,ωn的最小公倍数，ω是激励频率。

(8)

式中：

(9)

引入式(9)是为了描述一个完整周期T内的“平均功率”。其中，PT表示传递力在一个周期内 “功率”的平均值，P0表示激励力在一个周期内 “功率”的平均值，由于引入了T=2aπ/ω，该式可以包含亚谐波、超谐波甚至拟周期和混沌振动的多种情况[9]。

(10)

其位移与记忆恢复力的关系如图3所示。

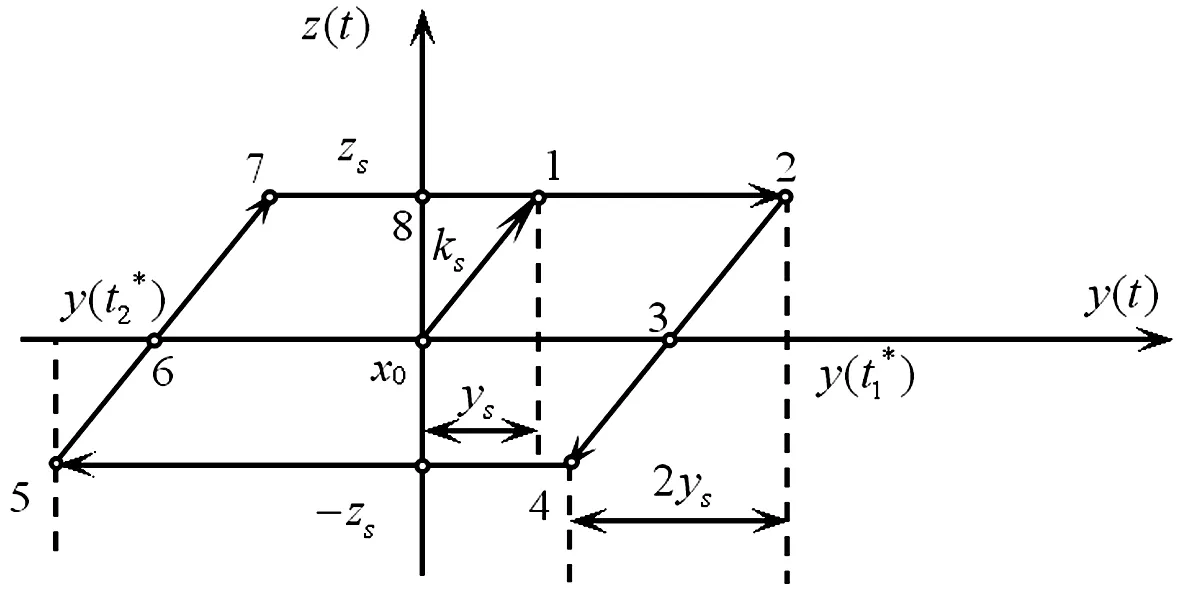
图3 双折线本构关系

考虑其增量方程并进行Fourier级数展开得[1]：

(11)

其中：

(12)

若以峰值到达的时间点为界限，则一个周期内传递力的平均功率精确表达为：

(13)

将计算得到的传递力“平均功率”PT和激励力“平均功率”P0一个周期内的平均功率代入(8)式，即可获得精确的系统振动传递率。由于式(8)中传递率的表达式是关于激励频率ω的函数，可通过该式获得精确的系统振动传递率幅频响应关系。到此便得到了金属橡胶隔振系统的精确解析解及系统的隔振特性。

3 算 例

由以上分析可知，不同系统的响应解形式及所对应的谐波组合都不同，合理选择必要的谐波分量、确定响应中主要的频率成分是求解的关键。

由系统响应的频谱图4(b)可知，系统的主要谐波成分不仅有单一谐波(ω=10)成分，还有亚谐波(ω=1.95)成分，且亚谐波为主要成分。针对这两个频率，结合(3)式和(6)式，解得系统响应表达式为：

yF(t)=4.604cos(3.90σπ×t+3.347 5)+

1.558cos(20πt+0.437 8)

(14)

用文献[4]的方法可求得单一谐波平衡法求得系统响应解的表达式为：

yD(t)=1.593cos(20πt+0.436 9)

(15)

单一谐波响应和FFT多谐波响应的解析解与数值解比较如图5所示。

再由式(14)计算出一个周期内各响应的极值点，并认为a近似取10，并代入式(9)，结合式(8)用数值方法可计算出FFT多谐波响应方法的振动传递率ηF≈0.213 5；利用式(8)、(9)、(15)三式联立可求得单一谐波平衡响应法的振动传递率为ηD≈0.149 1；计算得系统响应数值解的振动传递率ηS≈0.224 7。以数值解的振动传递率为准，比较两种方法的传递率与数值解的传递率可得：单一谐波平衡法求得的振动传递率的相对误差为30.16%；FFT多谐波平衡法求得的振动传递率的相对误差为5.24%。

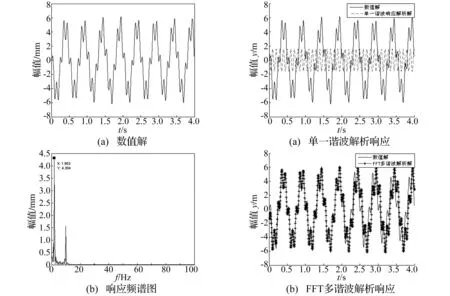
图4 系统响应数值解及频谱图

由以上分析可知，FFT多谐波响应的解析解与数值解基本吻合，而单一谐波平衡法的解析解与数值解相差很大，已经无法正确反映系统的响应。由此说明，金属橡胶非线性隔振系统响应存在多种谐波成分，单由激励频率为主导的单一频率的系统响应仅仅是个别情况，不能够准确反映系统的响应。

必须指出，非线性系统的幅值特性曲线并非单值。在激励频率的某些区间内，同一频率对应于振幅的多个不同值，系统响应取哪个稳定解，取决于系统的初始条件。同样，非线性系统的隔振传递率也非单值，不同初始条件对应不同的隔振传递率，因此确定非线性隔振系统的幅频响应曲线时，应首先说明系统的初始条件。Schlesing[6]以达芬方程为例对初始条件的影响做了详细的论述，这里不再赘述，感兴趣的读者可以查看该文献。

4 结 论

本文以金属橡胶非线性隔振系统为研究对象，用FFT多谐波平衡法研究了系统响应的解析解及某频率下的振动传递率，并通过算例比较了单一谐波平衡法和FFT多谐波平衡法的优劣，证明了FFT多谐波平衡法在分析金属橡胶非线性系统响应特性的适用性。

但是应该指出，该方法也有一定的局限性，当对系统响应数值解进行频谱分析时，如果有很多的频率成分，则FFT多谐波响应方法得到的系统解析解就比较复杂，且太多谐波分量的引入会增大计算的难度，为求解隔振系统的振动传递率带来很大的麻烦，求取系统一个周期内的平均功率也会非常复杂。例如当系统处于混沌状态时，频率成分太多且频谱的幅值不能被忽略。该问题需要进一步的研究。

[1]白鸿柏,张培林,郑坚,等. 迟滞振动系统及其工程应用[M]. 北京:科学出版社,2002.

[2]白鸿柏,黄协清.干摩擦振动系统响应计算方法研究[J]. 振动工程学报,1998,11(4):472-476.

BAI Hong-bai, HUANG Xie-qing. Study on response computation of dry friction damped vibration system[J]. Journal of Vibration Engineering. 1998,11(4):472-476.

[3]白鸿柏,张培林,黄协清.干摩擦动力吸振器简谐激励响应计算的最优化方法研究[J]. 振动与冲击,2000, 19(3): 43-45.

BAI Hong-bai, ZHANG Pei-lin, HUANG Xie-qing. Study on the response computation method of a two degrees-of-freedom vibration absorber system with variable coefficient of sliding friction using optimum approximate technique[J]. Journal of Vibration and Shock, 2000,19(3):43-45.

[4]路纯红,白鸿柏,李冬伟,等.含有三次非线性的粘性阻尼双线性迟滞振动系统的响应计算[J]. 振动与冲击, 2007,26(1):133-135.

LU Chun-hong, BAI Hong-bai, LI Dong-wei, et al. Response computation of a vibration system with viscous damping and nonlinear restoring force including bilinear hysteretic fricition and cubic displacement terms[J]. Journal of Vibration and Shock,2007,26(1):133-135.

[5]Masri S F. Forced vibration of the damped bilinear hysteretic oscillator[J]. J. Acoust. Soc. Am.,1975,57(1): 106-112.

[6]Schlesinger A.Vibration isolation in the presence of coulomb friction[J]. J. Sound and Vibration,1979, 63(2):213-224.

[7]Carrella A, Brennan M J, Kovacic I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009,322:307-317.

[8]Hamdan M N.,Burton T D. On the steady state reponse and stability of non-linear oscillators using harmonic balance[J]. Journal of Sound and Vibration, 1993,166(3):255-266.

[9]徐道临,吕永建,周加喜,等. 非线性隔振系统动力学特性分析的FFT多谐波平衡法[J]. 振动与冲击,2012,31(22): 39-44.

XU Dao-lin, LÜ Yong-jian, ZHOU Jia-xi, et al. FFT multi-harmonic balance method for dynamic analysis of a nonlinear vibration isolation system[J]. Journal Vibration and Shock, 2012,31(22):39-44.

[10]傅衣铭. 结构非线性动力学分析[M]. 广州:暨南大学出版社,1997.