环形密封对离心泵转子系统稳定性影响的数值研究

周文杰, 王乐勤, 邢桂坤, 翟璐璐 , 魏雪松 , 吴大转

(1.浙江大学 化工机械研究所，杭州 310027； 2.中国寰球工程公司，北京 100029)

转子-密封系统常见于农业灌溉的离心泵中。随着转速的不断提高，离心泵转子-密封系统将出现非线性特征，转子密封处的自激力将对转子系统产生很大影响，导致转子的强烈振动甚至失稳[1]。

对于转子-密封系统的非线性和稳定性研究，国内外学者已经做了许多相关研究工作，Muszynska等[2-4]在大量实验和数据分析的基础上引入了流体环向平均流速比，建立了非线性密封Muszynska模型，该模型已成为研究非线性密封的经典模型；Noah等[5]分析了线性密封模型的局限性并指出转子系统考虑非线性密封模型的重要性；Ding等[6]采用Muszynska模型和Poore定性进行了转子-密封系统稳定性分析，但是只是针对完美平衡的对称转子-密封系统，具有一定的局限性；李松涛等[7-10]对迷宫密封等多种密封形式的转子-密封系统进行了非线性动力稳定性和分岔研究，拓展了非线性转子-密封系统的密封结构，研究结果表明迷宫密封的参数对转子-密封系统的振动和稳定性有着十分重要的影响；薛丽辉等[11]得到了油膜力、气流力和密封力三种非线性力作用下的高参数涡轮转子复杂系统响应，但研究只是针对单跨对称涡轮转子的特别情况，而并非实际涡轮转子；何立东等[12]建立了三维转子密封流固耦合模型，通过直接对密封流场的非线性气动力进行数值求解，得到了流固耦合效应的转子密封气流激振问题的分析方法，但对象只是简单的转子-密封系统，对于复杂的情况还需进一步研究；罗跃纲等[13]则建立了带有裂纹故障的双跨弹性转子系统的动力学模型，研究了非线性油膜力下转子系统周期运动的稳定性及失稳规律，结果表明在亚临界转速区和超临界转速区具有不同形式的倍频及峰值。

本文通过将打靶法和Floquet理论相结合，对离心泵转子-环形密封系统的非线性稳定性及其分岔问题进行了研究，同时利用四阶Runge-Kutta法对不同密封几何参数情况下的离心泵转子-密封系统进行数值求解，得到了密封参数对系统稳定性的影响规律和离心泵转子-密封系统在不同密封参数下的分岔图、轴心轨迹、相图和庞加莱映射，计算结果为离心泵转子-密封系统的设计以及定性的控制转子系统的稳定性提供了理论依据。

1 转子环形密封动力学模型

图1左边所示为离心泵转子系统，考虑环形密封后转子-密封系统可以简化为右图所示，转子两端简支，环形密封位于圆盘轴向外侧，其密封力等效作用于圆盘处，由于圆盘存在不平衡偏心量将产生涡动(图中密封处为夸张表示)，圆盘质量为md，偏心距为e，圆盘转子处的阻尼为Cd，刚度为Kd，转子转速为ω，密封力为Fx、Fy，g为重力加速度，x、y为与转轴轴向垂直的横向振动坐标，t为时间，系统动力学方程可以写为：

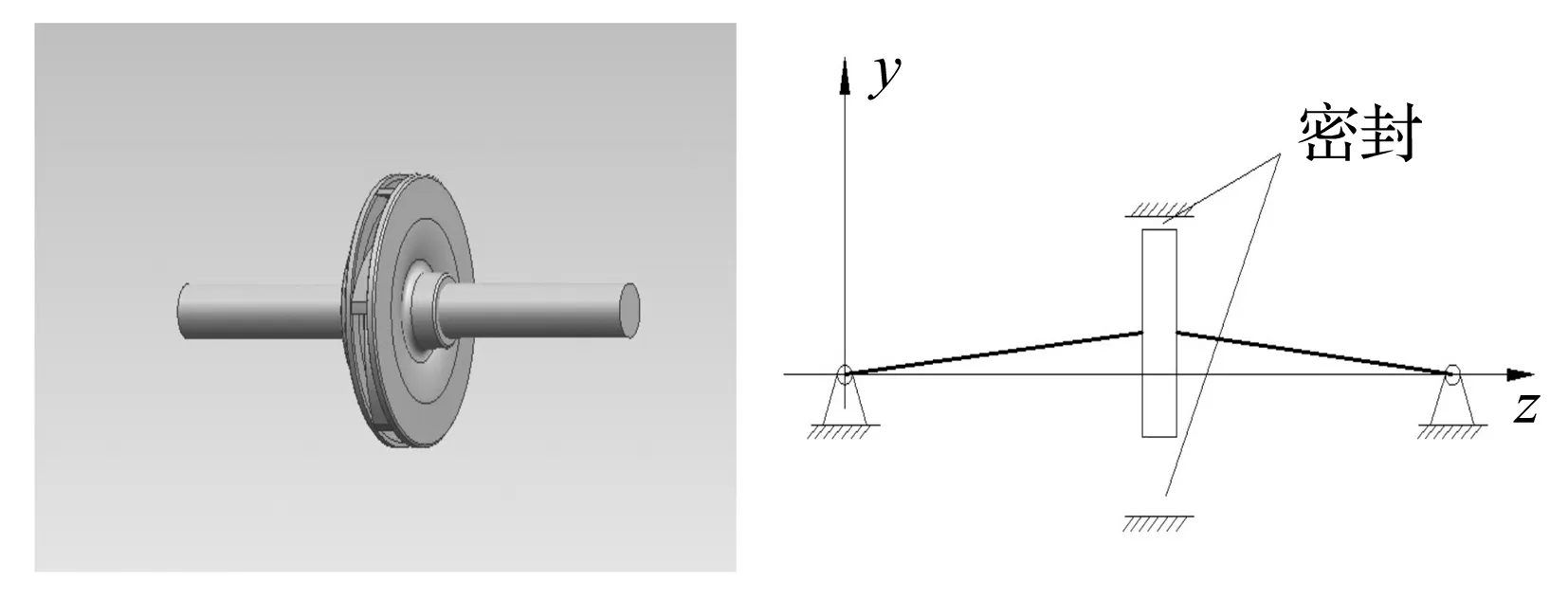
图1 转子-密封系统动力学模型

(1)

式(1)中密封力Fx、Fy采用非线性的Muszynska模型[3-4]，模型的特点是密封激振力对转子的扰动反力以某固定角速度绕轴颈旋转，其旋转效应是诱发转子失稳的主要因素，该反力可以表述为：

(2)

实验和数值研究结果证明式(2)中Ks、γ、Cs分别是密封刚度、密封流体周向平均速度与转速的比值和密封阻尼，并且三者均是位移x、y的非线性函数，即

Ks=K0(1-ε2)-n1,

Cs=C0(1-ε2)-n1,n1=0.5～3

γ=γ0(1-ε2)n2,n2=0～1，γ0<0.5

式中:ε=(x2+y2)1/2/ξ为转子相对偏心，ξ为密封间隙，K0、C0和ms三个动特性系数可以用Childs的环压密封动力系数公式计算。

引入无量纲变换：

X=x/ξ,Y=y/ξ,t′=ωt

则等式(1)变为

(3)

式中：

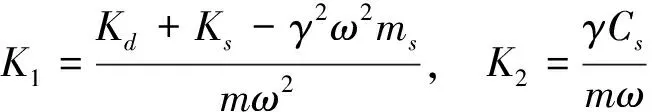
G=-mdg/(mω2ξ),ρ2=mde/(mξ)

将式(3)的二阶方程转化成一阶方程，然后采用四阶Runge-Kutta法对一阶方程进行数值求解，即可得到转子-密封系统瞬时响应。

2 Floquet理论

Floquet理论[14]是研究非线性动力系统稳定性周期解分岔问题的一种方法。

对于一个给定的参数ω=Ω和对应的周期稳态解X(t,Ω)=X(t+T,Ω)，其摄动方程可写为：

(4)

这里A(t)=A(t+T)是一个周期为T的n×n矩阵函数，其具体形式为：

(5)

右边非线性函数的Jacobi矩阵在周期稳态解处的值，即：

(6)

由线性方程叠加原理，式(4)的任意n个线性独立解为列的矩阵函数为其解矩阵：

Y(t)=[V1(t),V2(t),…,Vn(t)]∈Rn×Rn

(7)

式(4)的任意解都可以表示成：

V(t)=Y(t)BB={b1,b2,…,bn}T∈Rn

(8)

式中B是根据初始条件决定的常矢量。

由于Y(t)是式(4)的一个基解矩阵，则存在一个非奇异的T周期矩阵Φ(t)=Φ(t+T)和常数阵D，使：

Y(t)=Φ(t)exp(tD)

(9)

根据式(4)中A(t)的周期性特点，若Y(t)是式(4)的一个基解矩阵，则有：

A(t)Y(t+T)

(10)

由式(9)可得：

Y(t+T)=Φ(t+T)exp[(t+T)·D]=

Φ(t)exp(tD)exp(TD)=

Y(t)exp(TD)=Y(t)·C

式中C=exp(TD)为一常数阵。常数阵C与D的具体形式取决于Y(0)的选取，当然也与A(t)有关，定义矩阵C的特征值λ为Floquet乘子。

根据Floquet理论，当所有Floquet乘子的模都小于1时，系统是稳定的；当一个Floquet乘子通过(-1,0)穿出单位圆，而其它乘子的模都小于1时，系统产生倍周期分岔；当一个Floquet乘子通过(+1,0)穿出单位圆，而其它乘子的模都小于1时，系统产生鞍结分岔；当一对共轭复Floquet乘子穿出单位圆，而其它乘子的模都小于1时，系统产生Hopf分岔。

3 打靶法

打靶法是求解非线性振动周期解问题的常用方法[15]，对于非线性周期解，实质上就是求解如下形式微分方程：

(11)

为求解式(11)，r为x函数的初值和终值的差值，引入待定参数矢量s，使其满足边界条件：

r(s)=x(0,s)-x(T,s)=0

x∈Rm,f∶R·Rm→Rn

(12)

此时式(11)可以写成：

(13)

式中:x0、xT分别为t=0和t=T时解矢量的初值和终值，g(x)为方程与s有关的部分。

其次，要控制情绪，保持乐观向上、不急不躁的心态。因为情绪激动可使肾上腺素分泌增加，内耳小动脉血管发生痉挛，内耳供氧不足导致突发性耳聋。

利用牛顿迭代法，将式(12)在第i次近似值si附近展开成泰勒级数，取其线性部分：

(14)

式中:Δsi=si-s(i+1)为参数矢量si的第i次修正量，而

(15)

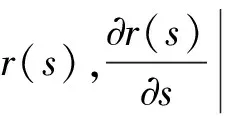
(16)

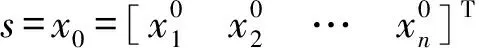
(17)

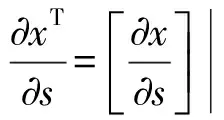
(18)

4 数值计算结果

初始密封基本参数和圆盘质量等其余参数如表1所示，分岔图如图2(a)所示，转速为6 800左右时转子—密封系统将产生Hopf分岔，系统将从稳定状态变成失稳状态。

表1 计算初始参数表

图2 不同密封参数分岔图

图3(a)是转速为2 000 r/min时的系统响应，从轴心轨迹可以看出，此时的转子的涡动轨迹呈现椭圆形，在原点周围稳定运行，涡动量很小，并且庞加莱映射只存在一个独立点，说明系统具有特定的周期，在图4(a)的频谱图只有一个频率；当转速上升到8 000 r/min时，轴心轨迹将不再是椭圆，而变得十分复杂，涡动值与转速较低时相比也增大了许多，并且开始变得发散，庞加莱映射由多个点集形成一个闭合曲线，说明此时转子-密封系统已经由周期性稳定运动变成了准周期运动，在图4(b)的频谱图中也不再是单一频率，出现了低频的分频，说明系统存在多个周期，也证明了此时系统是不稳定的准周期运动。

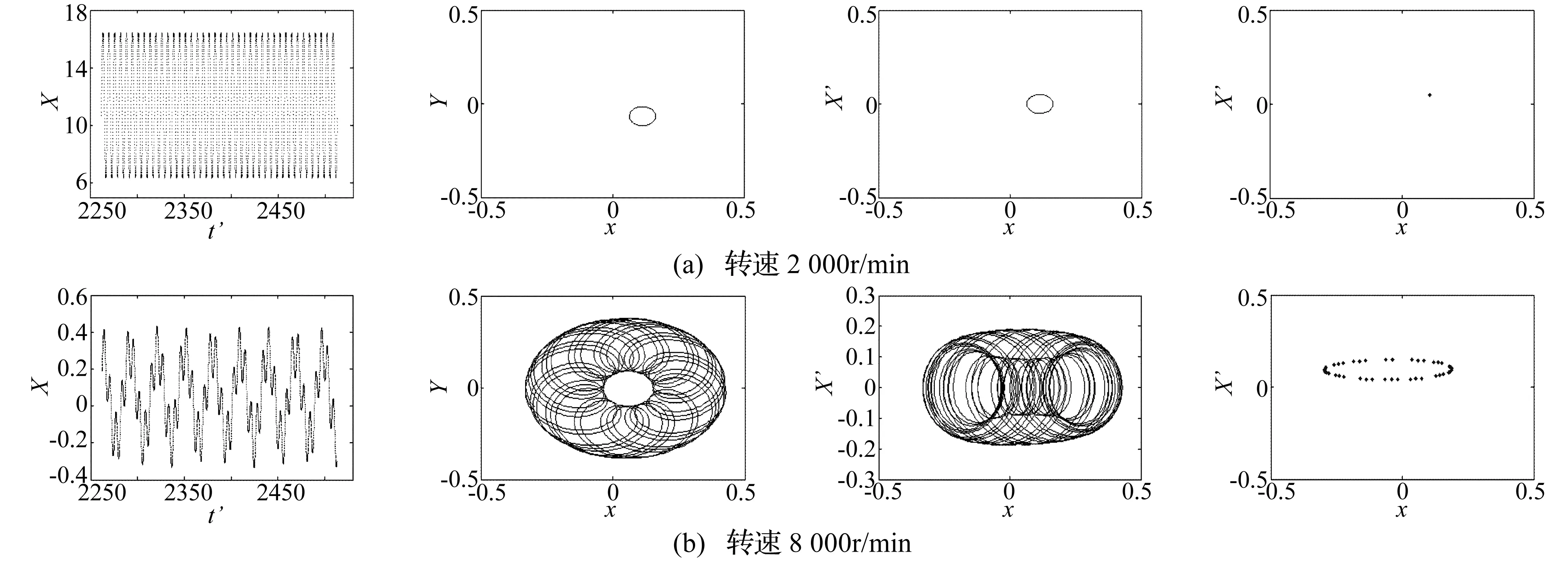
图3 初始参数下不同转速系统响应图

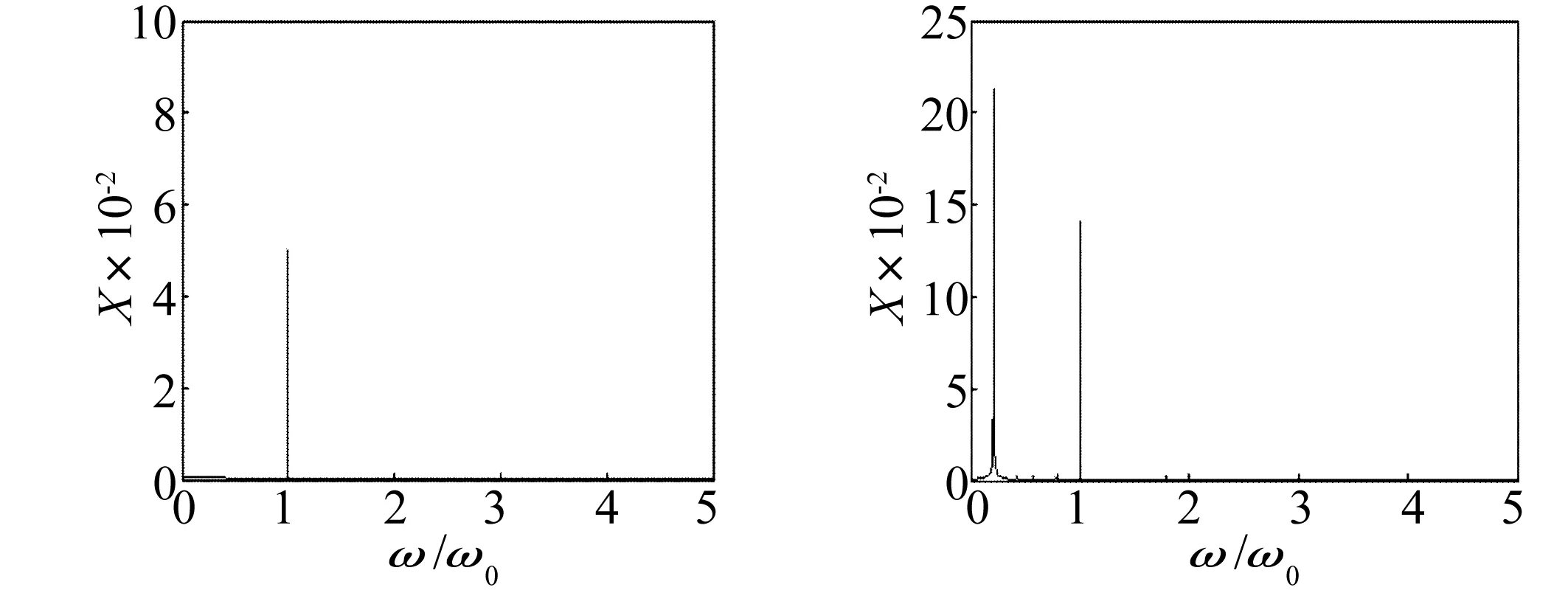
图4 初始参数下不同转速系统频谱图

改变环形密封两边压差，将原先0.75 MPa增大至1.2 MPa，其余密封参数保持不变。由图2(b)可知，压差增大，转子-密封系统产生Hopf分岔的失稳转速略有提高，说明适当增大压差有利于离心泵转子-密封系统的稳定性。图5可以看出，转速为7 300 r/min时，系统由稳定涡动运行逐渐变得不再稳定，涡动幅值将逐渐变大，轴心轨迹呈现发散迹象，此时的庞加莱映射不是独立的一点，而是多个点，并且有形成一闭合曲线的趋势，说明转速增大系统将进入准周期运动。

图2(c)和图2(d)分别为保持其余参数不变，增大密封间隙至0.001 2 m和增加密封长度至0.12 m时的分岔图，由图2(a)比较可知，增大密封间隙和密封长度将使失稳转速略有降低，降低转子-密封系统的稳定性，但相对增加压差和增加密封长度而言，增大密封间隙对系统的稳定性影响相对较小。图6和图7为增大密封间隙和增加密封长度的系统响应图，在转速为9 000 r/min时，由于转速较快，系统失稳呈现准周期运动，轴心轨迹以及相图均是发散状态，庞加莱映射为一闭合曲线。与初始状态相比，此时的涡动幅值更大，若继续提高转速，转子-密封系统将会与离心泵壳体发生碰摩事故。

图5 压差1.2 MPa转速7 300 r/min系统响应图

图6 间隙0.001 2 m转速9 000 r/min系统响应图

图7 长度0.12 m转速9 000 r/min系统响应图

表2为利用打靶法和Floquet理论计算得到的系统失稳转速时的Floquet乘子，在初始密封参数情况下系统失稳转速为6 680 r/min，增大密封压差，增大密封间隙及增加密封长度时失稳转速将分别达到7 180 r/min,6 640 r/min和6 540 r/min，这与图2利用四阶Runge-Kutta法计算得到分岔图中失稳转速基本是一致的。

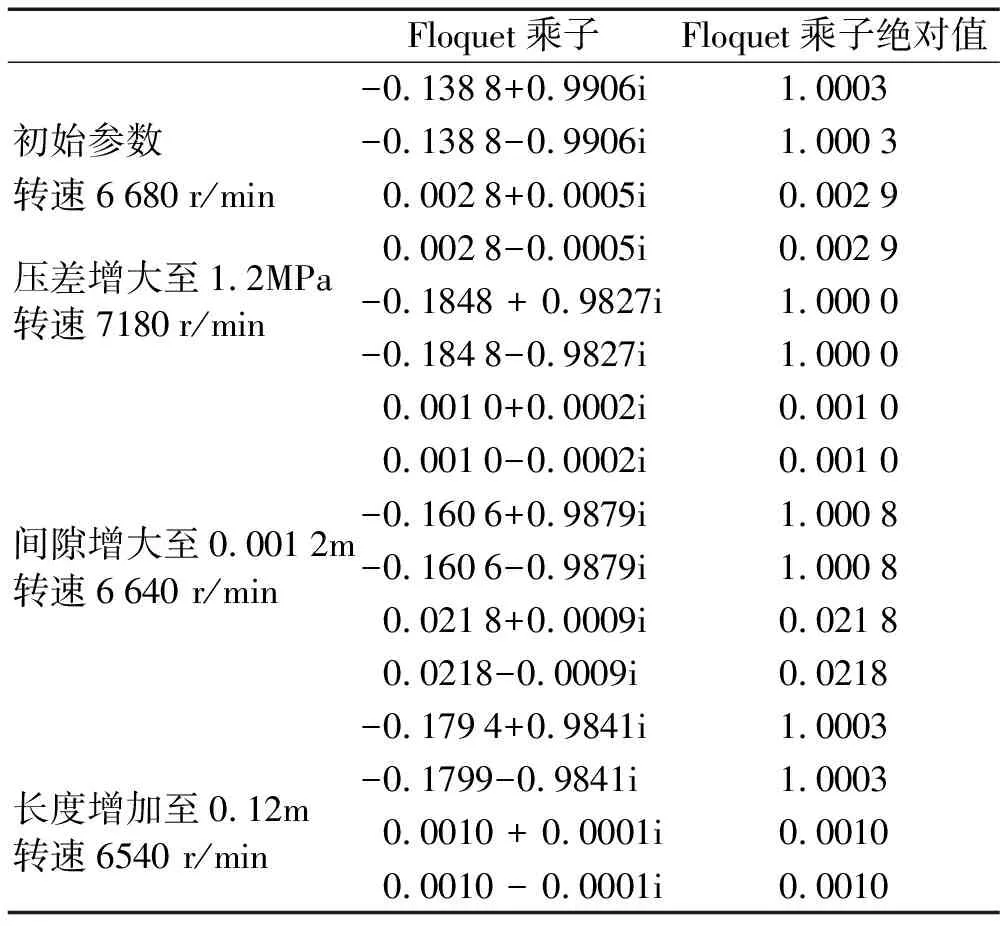
表2 失稳转速时的Floquet乘子

5 结 论

(1) 环形密封中的流体激励力是离心泵转子-密封系统失稳的重要因素。在转速较低时，转子-密封系统呈现出稳定的周期涡动，随着转速的增大，系统将出现Hopf分岔而失稳。

(2) 采用非线性密封Muszynska模型建立了转子-密封系统动力学模型，同时利用四阶Runge-Kutta法对离心泵转子-密封系统进行数值求解，并将打靶法和Floquet理论相结合，较准确的求解得到了不同密封参数下系统的失稳转速。

(3) 适当增大压差、减小密封间隙和减小密封长度均会提高离心泵转子-密封系统出现Hopf分岔的失稳转速，在离心泵转子-密封系统的设计和失稳控制中可以采用以上措施提高系统的可靠性和稳定性。

[1]IWATSUBO T，SHENG B C. Evaluation of seal effects on the stability of rotating fluid machinery[J]. International Journal of Rotating Machinery, 1995, 2(2): 85-92.

[2]Muszynska A. Improvements in lightly loaded rotor/bearing and rotor/seal models[J]. Journal of Vibration Acoustics, Stress and Reliability in Design, 1988, 110(2): 129-136.

[3]Tam L T, Przekwas A J, Muszynska A, et al. Numerical and analytical study of fluid dynamic forces in seals and bearings [J]. Journal of Vibration Acoustics, Stress and Reliability in Design, 1988, 110(3): 315-325.

[4]Muszynska A, Bently D E. Frequency-swept rotating input perturbation techniques and identification of the fluid force models in rotor/bearing/seal systems and fluid handling machines [J]. Journal of Sound and Vibration. 1990, 143(1)：103-124.

[5]Noah S T, Sundararajan P. Significance of considering nonlineareffects in predicting the dynamic behavior of rotating machinery[J]. Journal of Vibration and Control, 1995, 1(4): 431-458.

[6]Ding Q, Cooper J E, Leung A Y T. Hopf bifurcation analysis of a rotor/seal system[J]. Journal of Sound and Vibration, 2002, 252(5): 817-833.

[7]李松涛，许庆余，万方义. 迷宫密封转子系统非线性动力稳定性的研究[J]. 应用力学学报，2002，19(2)：27-30.

LI Song-tao, XU Qing-yu, WAN Fang-yi. A study on nonlinear dynamic stability of labyrinth seal-rotor system[J]. Chinese Journal of Applied Mechanics，2002，19(2)：27-30.

[8]Li S T, Xu Q Y, Zhang X L. Nonlinear dynamic behaviors of a rotor-labyrinth seal system[J]. Nonlinear Dynamics, 2007, 47(4): 321-329.

[9]刘思涌，薛自华，陆圯，等. 迷宫密封-转子系统非线性动力学模型及求解[J]. 振动与冲击，2012，31(13)：41-45.

LIU Si-yong, XUE Zi-hua, LU Yi, et al. Nonlinear dynamic model of labyrinth seal-rotor system and its solution[J]. Journal of Vibration and Shock, 2012, 31(13): 41-45.

[10]Wang W Z, Liu Y Z, Meng G, et al. Nonlinear analysis of orbital motion of a rotor subject to leakage air flow through an interlocking seal[J]. Journal of Fluids and Structures, 2009, 25(5): 751-765.

[11]薛丽辉，曹树谦. 三种非线性力作用下高参数涡轮转子复杂运动响应[J]. 工程力学，2011，28(7)：210-216.

XUE Li-hui, Cao Shu-qian. Complex response of a high-parameter turbo rotor model under three nonlinear forces[J]. Engineering Mechanics, 2011, 28(7): 210-216.

[12]何立东，高金吉，金琰，等. 三维转子密封系统气流激振的研究[J]. 机械工程学报，2003，39(3)：100-104.

HE Li-dong, GAO Jin-ji, JIN Yan, et al. Study on gas flow-induced vibration for a three-dimensional rotor-seal system[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 100-104.

[13]罗跃纲，张松鹤，刘晓东，等. 含裂纹双跨转子一轴承系统周期运动的稳定性[J]. 农业机械学报，2007，38(5)：168-172.

LUO Yue-gang, ZHANG Song-he, LIU Xiao-dong, et al. Stability of a two-span, rotor-bearing system with crack fault[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(5): 168-172.

[14]吴浩. 可倾瓦滑动轴承—转子系统非线性动力学特性分析[D]. 哈尔滨：哈尔滨工业大学，2007.

[15]周纪卿，朱因远. 非线性振动[M]. 西安：西安交通大学出版社，1998.