功能梯度泡沫动力学响应分析
卢富德,高 德
(浙江大学 宁波理工学院,宁波 315100)
在缓冲包装或头盔领域,一些学者研究了层状缓冲结构的压缩响应及吸收能量特性。Sek[1]试验方法研究多层瓦楞纸板结构的缓冲性能,拓展了瓦楞纸板作为缓冲包装材料的可能。卢富德[2-3]提出虚拟质量方法,求解多层瓦楞纸板静态、动态压缩响应,Lu等[4]研究发泡聚苯乙烯与发泡聚乙烯串联结构动力学响应。Coelho等[5]运用显式有限元研究EPS与软木串联应用的头盔结构,文献[6]考虑外包装箱作用,研究瓦楞纸板与发泡聚乙烯的冲击响应及结构的优化设计。
以上文献研究对象都是层状结构,最近出现功能梯度缓冲材料,此功能梯度材料的密度随厚度方向按照一定的函数变化,它克服了层状结构界面易开裂等缺点[7]。Cui等[8-9]用有限元方法研究层状泡沫与梯度泡沫在头盔中的优化,把梯度泡沫按照近似的层状结构进行处理。报道的文献对梯度泡沫的压缩响应研究还比较少,仅限于有限元方法,还需要寻求梯度泡沫的响应简便方法。
鉴于此,本文运用Runge-Kutta法研究功能梯度泡沫缓冲结构动力学响应规律,为工程优化设计提供有效方法。
1 功能梯度泡沫一维本构
典型泡沫结构应力-应变曲线由线弹性区、屈服平台区及压实区组成。泡沫弹性模量、屈服强度与实体塑料弹性模量、屈服强度有关[8],即
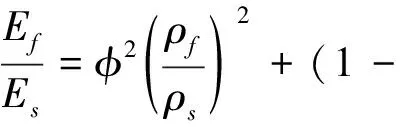
(1a)
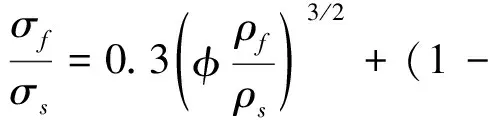
(1b)
(1c)
式中:Ef为泡沫弹性模量,Es为塑料实体的弹性模量,σf为泡沫平台应力,σs为塑料实体的屈服应力,ρf为泡沫的密度,ρs为塑料实体的密度,Φ为单位体积上边上固体部分,1-Φ为单位体积上面上固体部分。
如图1所示,双曲正切函数与正切函数的特点,典型泡沫的本构关系可由下式表示[10]:
(2)
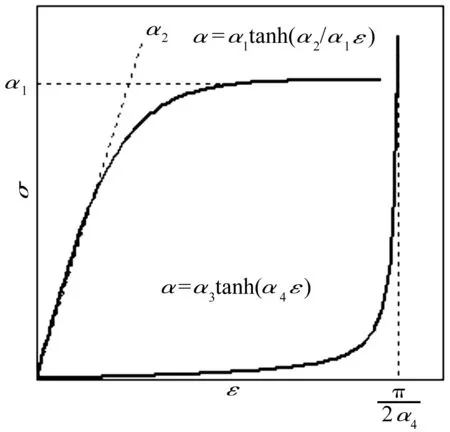
图1 双曲函数与正切函数的特征
泡沫结构线弹性、屈服段及压实段的本构可以由下式表示[10]
(3)
式中:α为控制应力-应变曲线平台的斜率。
由聚苯乙烯的Es=3.3 GPa,σys=15 MPa,ρs=1 050 kg/m3,Φ=0.52,α=4 kPa等参数[9],由式(3)可得近似发泡聚苯乙烯EPS的应力-应变曲线,如图2所示。图2所示,随泡沫密度的增加,泡沫屈服平台应力增加,其压实应变却减小。
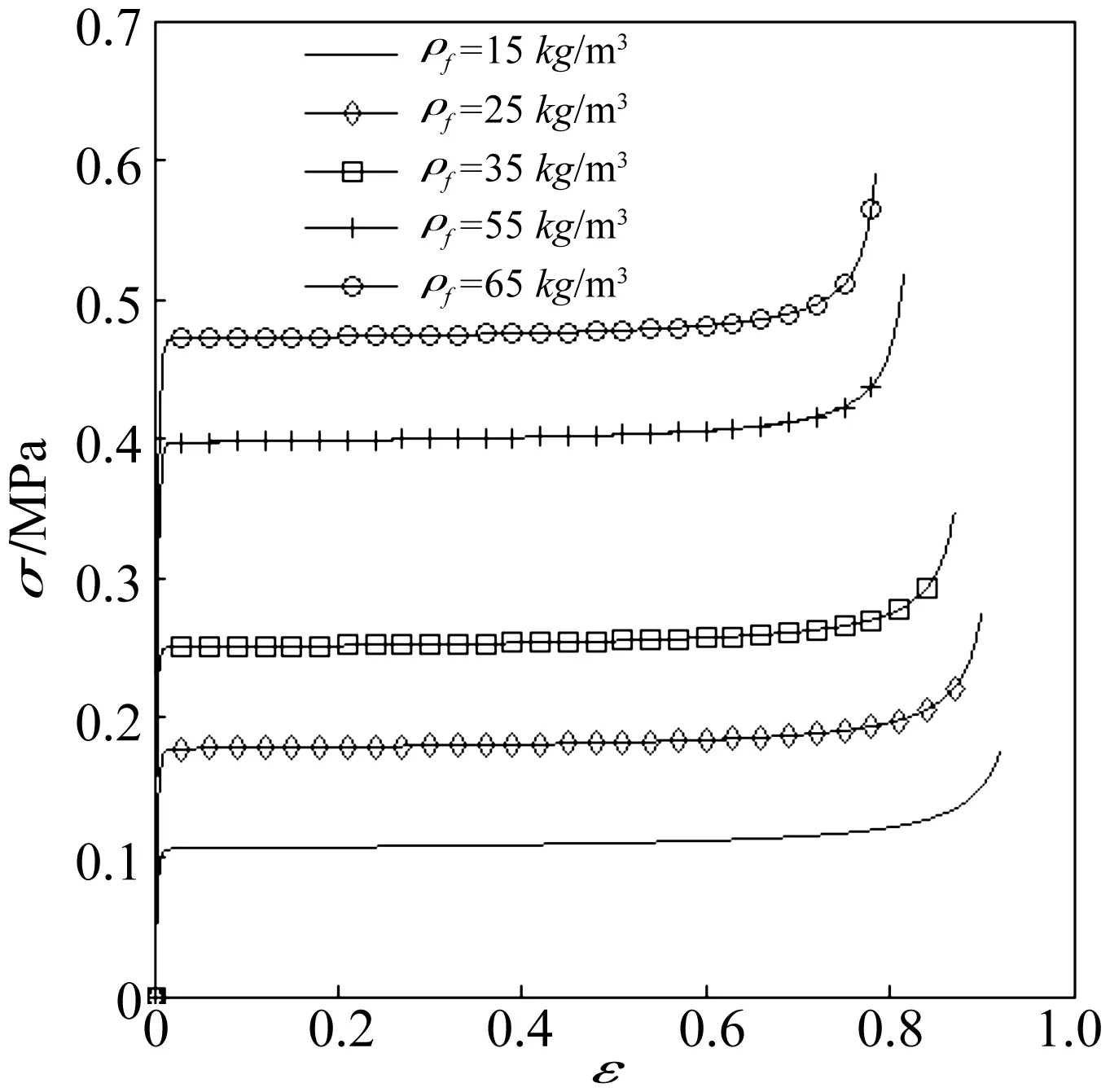
图2 应力与应变、相对密度的关系
2 功能梯度泡沫系统模型
质量为m的物体,以一定的速度冲击梯度泡沫缓冲结构,为了建模的方便,把泡沫分成n层,近似模拟连续的功能梯度函数变化,如图3所示为功能梯度泡沫系统动力学模型。
梯度函数为指数函数,下式所示[7]
(4)
由式(4)得到梯度泡沫平均密度ρave
(5)
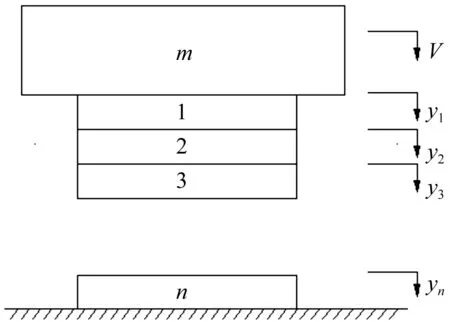
图3 功能梯度泡沫系统冲击模型
式中:ρfi(i=1,2,…n)为第i层的密度,ρ1为上层的密度,ρ2为最下层的密度,M为指数。
由牛顿定律得系统动力学方程:
式中:m1为每一层的等效质量,A为泡沫的横截面积,h为每层的厚度,
初始条件为:
y1(0)=y2(0)=…=yn(0)
(7)
3 数值结果
m=6 kg,m1=0.01 kg,n=11,h=0.003 64 m,Es=3.3 GPa,σys=15 MPa,ρs=1 050 kg/m3,Φ=0.52,α=4 kPa。
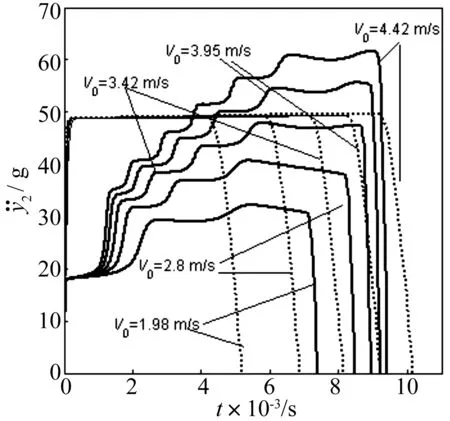
图曲线(ρave=40 kg/m3 ,Δρ=50 kg/m3)实线:梯度泡沫系统响应,点划线:均匀泡沫响应响应
取V=1.98,2.8,3.42,3.95,4.42 m/s,求质量块的加速度响应,加速度是衡量缓冲冲击响应的一个标准[10-11],本文研究加速度响应与一些参数的关系,本文仅考虑压缩阶段的冲击响应,不考虑泡沫回弹阶段的结果。
如图4所示,具有均匀密度为40 kg/m3的泡沫,当m=6 kg的物体冲击时,其最大响应加速度为49.34 g(g=9.8 m/s2),不随冲击速度的变化而变化;当冲击速度1.98,2.8,3.42,3.95与4.42 m/s时,其最大加速度分别为32.15,40.67,48.02 g,55.84和61.77 g,冲击能量较小时,梯度泡沫响应加速度小于均匀泡沫,故梯度泡沫对较小能量有利。
取M=0.2,0.5,1,2,3,4,5和10,分析梯度函数对梯度泡沫结构冲击响应的影响,在V=1.4~5.4 m/s范围,也就是初始输入能量为5.88~88.2 J时, 取Δρ分别为25,50和75 kg/m3,对平均密度为70 kg/m3的梯度泡沫进行分析,以说明梯度Δρ对泡沫冲击响应的影响。以梯度泡沫系统响应加速度除以均匀泡沫冲击响应为归一化的值作为应变量,以指数M及输入能量为自变量,得到结果如图5所示。

(a) Δρ=25 kg/m3 (b) Δρ=50 kg/m3 (c) Δρ=75 kg/m3
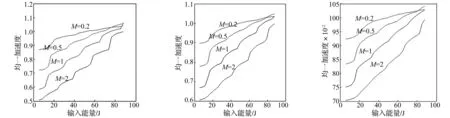
(a) ρ1=50 kg/m3 (b) ρ1=60 kg/m3 (c) ρ1=70 kg/m3
在图5中,当M=1,即为线性梯度的泡沫系统,在输入能量为5.88时,其均一化加速度值最小,随Δρ=25、50和75 kg/m3变化时,均一化加速度值分别为0.84、0.75及0.56,可以看出,梯度增大,小冲击能量冲击系统时,梯度泡沫系统响应会变小。
图6所示,ρave=100 kg/m3,ρ1分别取50、60与70 kg /m3时,均一化加速度与梯度函数的关系,在所给的例子中,均一化加速度随M的增大而减小。
4 结 论
基于泡沫的特点,建立了有效的本构关系。根据对泡沫系统动力学响应分析的结果,得到梯度泡沫系统对小能量的冲击响应比均匀泡沫密度系统要小,克服了均匀泡沫系统对一定冲击能量范围响应几乎不变化的特点,增加了泡沫的使用范围,为梯度泡沫的运用提供有效方法。
[1]Sek M, Rouillard V,Tarash H, et al. Enhancement of cushioning performance with paperboard crumple inserts[J]. Packaging Technology and Science,2005, 18(5): 273-278.
[2]卢富德,陶伟明,高德.串联缓冲结构压缩响应虚拟质量分析[J]. 浙江大学学报(工学版),2012,46(8):1431-1436.
LU Fu-de,TAO Wei-ming, GAO De. Compression responses of series cushioning structures by a virtual mass method[J]. Journal of Zhejiang University (Engineering Science), 2012,46(8):1431-1436.
[3]卢富德,陶伟明,高德.瓦楞纸板串联缓冲系统动力学响应[J]. 振动与冲击,2012 ,31 (21): 30-32.
LU Fu-de,TAO Wei-ming, GAO De. Dynamic response of a series cushioning packaging system made of multi-layer corrugated paperboard[J]. Journal of Vibration and Shock, 2012 ,31 (21): 30-32.
[4]Lu F D,Tao W M,Gao D.Virtual mass method for solution of dynamic response of composite cushion packaging system[J]. Packaging technology and Science,2013,26(S1):32-42.
[5]Coelho R M,Alves D, Sousa R J, et al. New composite liners for energy absorption purposes [J]. Materials & Design,2013, 43 :384-392.
[6]卢富德,陶伟明,高德. 串联缓冲系统冲击响应与结构优化分析[J]. 浙江大学学报(工学版),2012,46(10):1773-1777.
LU Fu-de,TAO Wei-ming, GAO De. Impact response of series cushioning system and structure optimization analysis[J]. Journal of Zhejiang University (Engineering Science),2012,46(10):1773-1777.
[7]Kieback B, Neubrand A, Riedel H. Processing techniques for functionally graded materials [J]. Materials Science and Engineering A,2003,362(1-2): 81-105.
[8]Cui L, Rueda M A F,Gilchrist M D. Optimisation of energy absorbing liner for equestrian helmets. Part II: Functionally graded foam liner[J]. Materials & Design,2009,30(9):3414-3419.
[9]Cui L, Kiernan S, Gilchrist M D. Designing the energy absorption capacity of functionally graded foam materials[J]. Materials Science and Engineering A,2009, 507(1-2): 215-225.
[10]高德,卢富德.考虑转动的双曲正切与正切组合模型缓冲系统冲击响应研究[J]. 振动工程学报,2012,25(1):6-11.
GAO De, LU Fu-de. The shock response of hyperbolic tangent and tangent comprehensive model on cushion system considering rotary motion[J]. Journal of Vibration Engineering, 2012,25(1):6-11.
[11]高德,卢富德.基于杆式弹性易损部件的非线性系统跌落冲击研究[J]. 振动与冲击,2012 ,31 (15): 47-49 ,59.
GAO De, LU Fu-de. Drop impact analysis of packaging system with bar type elastic critical components[J]. Journal of Vibration and Shock, 2012 ,31 (15): 47-49 ,59.
[12]高德,卢富德.聚乙烯缓冲材料多自由度跌落包装系统优化设计[J].振动与冲击,2012,31(3):69-72.
GAO De, LU Fu-de. Optimization design of MDOF package cushioning system made of polyethylene[J]. Journal of Vibration and Shock, 2012,31(3):69-72.

