基于响应面法的层间隔震结构地震易损性分析

张尚荣，谭 平，杜永峰，周福霖，赵丽洁

(1. 兰州理工大学 防震减灾研究所,兰州 730050；2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,兰州 730050；3. 广州大学 广州大学工程抗震研究中心, 广州 510405)

近期发生在我国的“4·20”芦山地震造成了大量房屋的破坏和倒塌。而对于采用隔震技术的芦山县人民医院门诊综合楼，经受了考验，表现出良好的抗震性能。层间隔震结构作为一种新型的结构体系，且迄今为止尚缺乏对层间隔震结构易损性的研究，所以理论分析是得到其易损性曲线的唯一可行方法。

响应面法应用比较广泛，目前已在很多领域得到成功运用，Bucher等[1]首次将响应面法引入土木工程领域，用于对结构可靠度的研究；Rajashekhar等[2]分别运用响应面法和传统的可靠度分析方法对比分析了钢筋混凝土板在不同界限状态下的可靠度。国内外对混凝土结构和桥梁结构的易损性进行了大量的研究，取得了许多成果。刘晶波等[3]考虑了结构本身及地震动的不确定性，提出了基于结构极限状态确定结构抗震性能水平限值的方法，对两个不同类型的方钢管混凝土框架结构进行基于性能的地震易损性分析。吕大刚等[4]结合拉丁超立方体抽样技术，提出一种能综合考虑地震动不确定性和结构不确定性的改进云图法,并将传统的概率地震需求分析内容拓展为概率地震需求模型、概率地震需求易损性分析、概率地震需求危险性分析三个层次。吴子燕等[5]考虑地震地面运动和结构本身的物理不确定性，以中心复合设计法建立地震动-桥梁结构试验样本对，对系统样本模型进行非线性时程分析，在此基础上采用蒙特卡洛模拟获得结构的易损性曲线。吴巧云等[6]综合考虑地震动峰值加速度及阻尼比为5%的谱加速度，考虑近场及远场地震的不同性质，对一钢筋混凝土框架房屋进行了地震易损性分析。朱健[7]系统介绍了常规钢筋混凝土结构、常见被动隔减震消能结构的易损性分析方法。

本文同时考虑了地震动和结构物理参数不确定性，提出一种基于响应面法的层间隔震结构的地震易损性分析方法。以中心复合设计方法建立地震动-层间隔震结构试验样本对，对系统样本模型进行非线性动力时程分析，分别建立层间隔震结构各子结构响应面模型，在此基础上采用蒙特卡洛模拟获得易损性曲线。

1 响应面模型的建立

1.1 响应面法的基本原理

响应面方法是一种结合数学应用、统计分析和试验设计的技术探讨影响因子与响应输出之间的数学模式关系，经由试验设计者在所关心试验区域内以系统的方式进行试验，取得所希望的响应值和因子水平[8]。

地震分析中，结构响应表现出非线性的特性，因此选用二次多项式作为响应面模型。其反应函数的表达式可以写为：

(1)

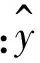
经过n次动力时程分析，得到关于待估参数γ0、γi、γii、γij的非齐次线性方程组，通过最小二乘回归分析得到待估参数的无偏估计，从而得到结构响应的近似函数。结构响应的均值和均方差分别表示为：

(2)

(3)

因此，结构的响应面模型就可以表示为[9]：

i=1,2,…,k

(4)

1.2 试验设计

试验设计就是系统地定义一套有效的试验取样点。本文选取中心复合设计方法(Central Composite Design, CCD)。中心复合设计是可以拟合二次完全析因设计的响应面设计。假设每个因子在-1和+1之间变化。确定的试验点一共有2k+2k+1个，包括2k个象限点，2k个轴线点和1个中心点。

1.3 适应性检验

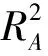
(5)

(6)

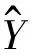
2 基于响应面方法的地震易损性分析方法

结构地震易损性分析中，有许多不确定性。其中对结构性能影响最重要的是材料强度和地震动不确定性。通过简化结构、确定合理分析模型，建立层间隔震结构地震动样本对，对建立的系统样本对进行非线性时程动力分析，建立响应面模型，通过蒙特卡洛模拟进行层间隔震结构性能评估，具体流程见图1所示。

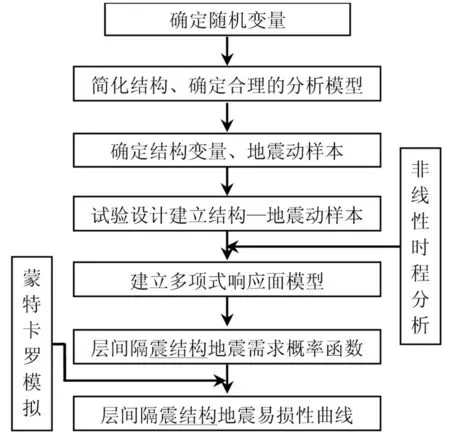
图1 基于响应面法的层间隔震结构易损性分析方法

3 工程典型分析

3.1 结构模型

选取一典型层间隔震框架结构为算例，建筑场地Ⅱ类，设计地震分组第一组，抗震设防烈度8°(0.2 g)，框架抗震等级2级。结构平、立面如图2所示；采用Opensees对结构进行弹塑性动力时程分析，由于结构对称，将结构简化为平面模型，取第③轴线的层间隔震结构一榀框架进行分析。其中钢筋本构模型选用Steel02、混凝土本构模型选用基于Kent-Scott-Park模型的Concrete02模型；梁、柱截面采用纤维截面模型；梁、柱单元选用基于有限单元柔度法的Beam With Hinges单元和nonlinear Beam Column单元；隔震层单元采用Iso2spring截面、zeroLengthSection单元。层间隔震结构最大平均水平向减震系数为0.345 8；大震时隔震层最大位移为285.34 mm；隔震层结构隔震前的基本周期为0.801 s，隔震结构分别采用ETABS、Opensees建模，基本周期表1所示。层间隔震结构结构有限元模型正确性得到校验。

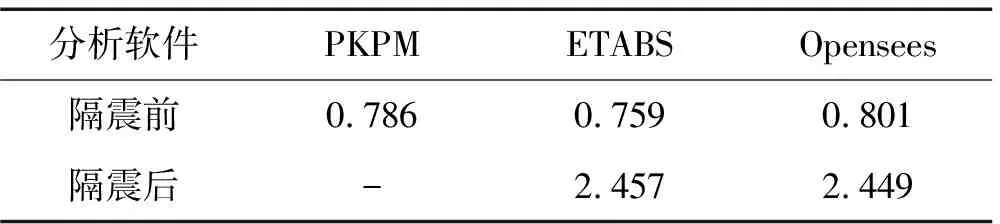
表1 结构周期

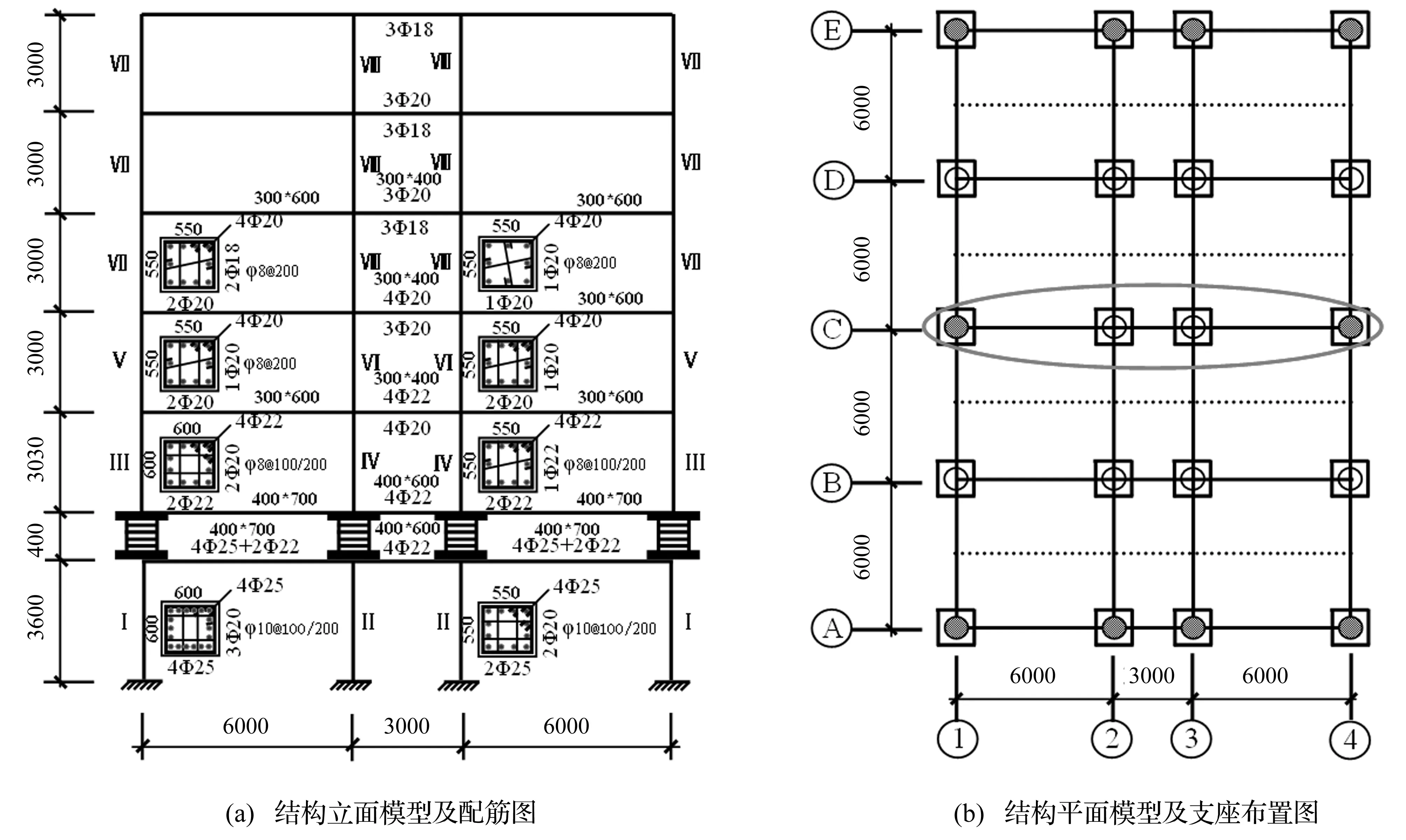
图2 结构模型

3.2 结构—地震动不确定性参数

结构随机参数选取钢筋、混凝土强度和隔震支座屈服后刚度3个因素，各参数特性如表2所示。假定支座屈服前刚度与屈服后刚度比为k1/k2=10，支座屈服力F=90.4 kN。研究中通过美国太平洋地震研究中心(PEER)数据库选取相当于二类场地的12条断层距大于20 km、震级大于6.5级、PGA/PGV=1.86～29.23的地震波，将所选地震记录调幅满足试验设计要求。各地震波的加速度反应谱和平均反应谱如图3所示。

表2 随机变量统计信息

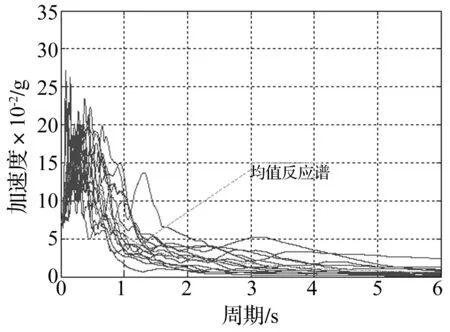
图3 地震加速度反应谱及均值反应谱

3.3 层间隔震结构的响应面模型分析

3.3.1 试验设计与结构响应计算

在试验设计中，需要将输入变量进行标准化，划分为上限值、下限值和中心值，分别用+1、0和-1与其对应。利用式(7)进行标准化，如表3所示。

(7)

3.3.2 响应面模型拟合

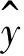
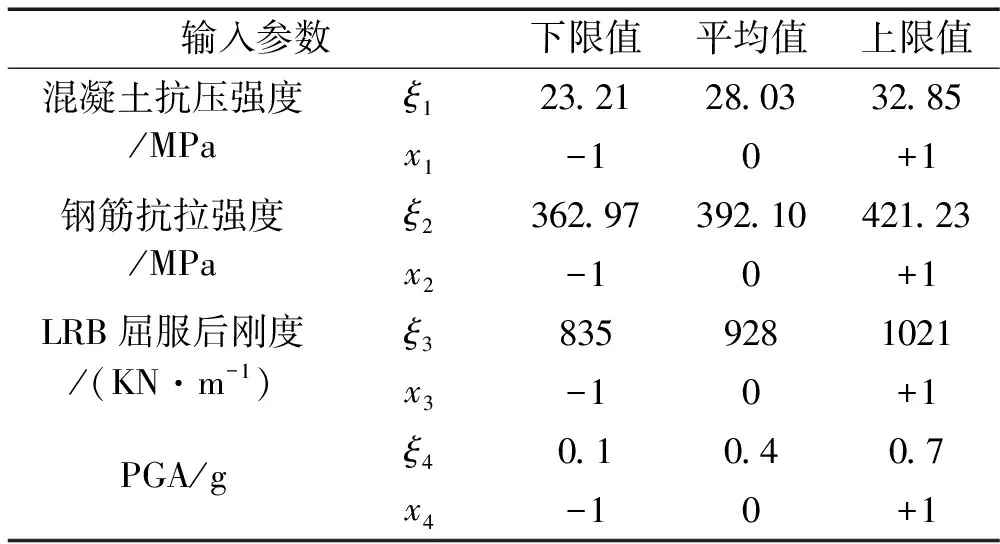
表3 输入参数及其标准化

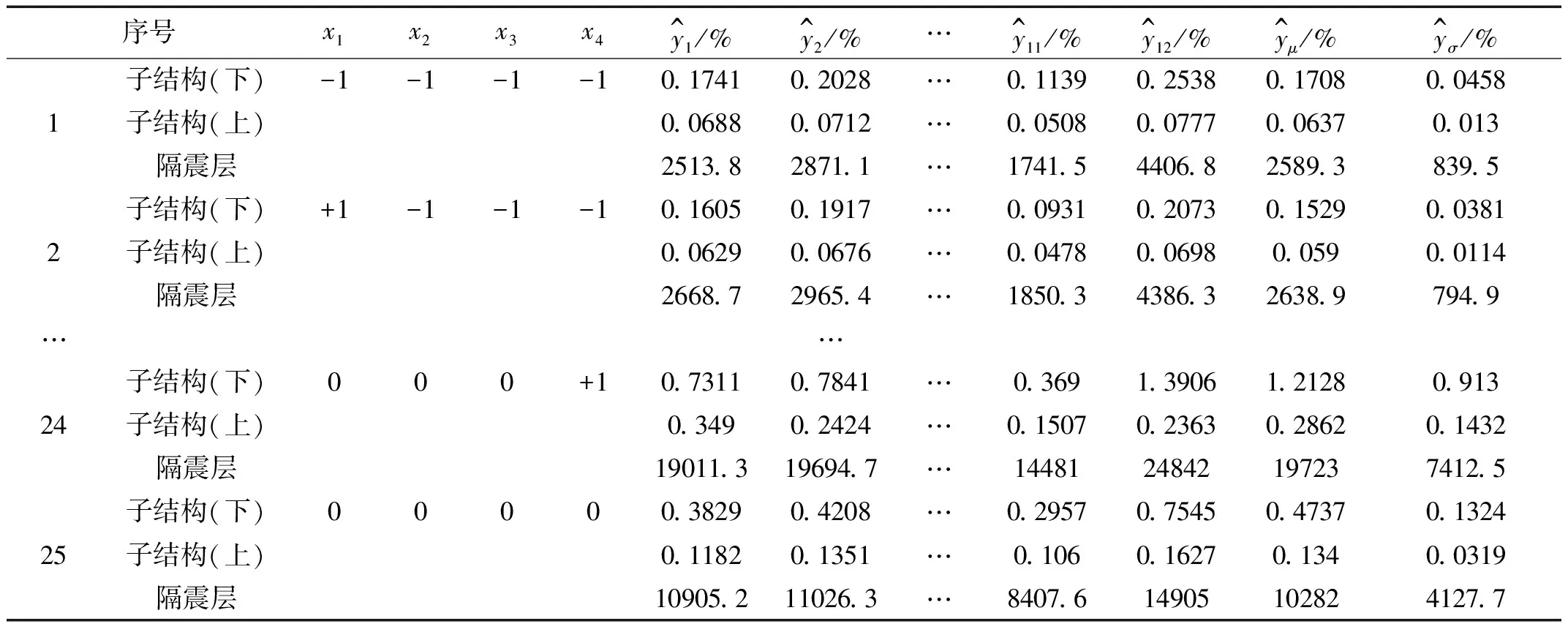
表4 试验设计及数值模拟结果

3.3.2.1 上部子结构最大层间位移角响应面函数

均值拟合多项式响应面函数：

0.000 4x1x2+0.000 2x1x3-0.007 8x1x4+

0.000 7x2x3+0.001 6x2x4+0.007 5x3x4

均方差拟合多项式响应面函数：

0.000 5x2x3+0.000 6x2x4+0.010 5x3x4

3.3.2.2 隔震层最大位移响应面函数

均值拟合多项式响应面函数：

0.23x1x3+0.73x1x4+0.24x2x3+2.86x2x4-4.28x3x4

均方差拟合多项式响应面函数：

0.29x1x3+1.20x1x4+0.08x2x3+2.32x2x4-2.87x3x4

3.3.2.1 下部子结构最大层间位移角响应面函数

均值拟合多项式响应面函数：

0.006 9x2x3-0.037 5x2x4+0.033x3x4

均方差拟合多项式响应面函数：

0.030 7x2x3-0.005 9x2x4-0.016 9x3x4

图4(a)、(b)、(c)表示各输入变量对各子结构响应的敏感性影响。纵向的二维条形图表示各输入变量对结构的重要性，可以很明显看出，地震动强度(x4)的变化对结构响应的影响大于其他的输入变量，即地震动峰值加速度(PGA)是最敏感因素。

图4 输入变量的pareto图

3.3.3 响应面模型适应性

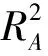
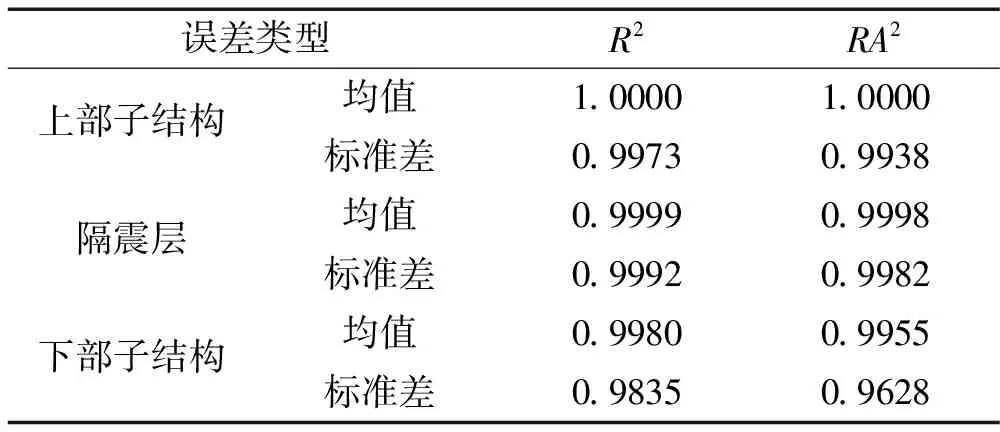
表5 响应面拟合系数

图5 真实最大层间位移角与预测层间位移角对比

由表5和图4可以看出，多重拟合系数和修正多重拟合系数均大于0.9，且上、下部子结构的真实最大层间位移角与预测层间位移角的比值均接近1。由此可知建立的多项式响应面函数拟合效果理想。

3.3 层间隔震结构的易损性分析

3.3.1 性能水平的确定

层间隔震结构由上部子结构、隔震层、下部子结构三部分构成，在地震作用下各子结构呈现出不同的破坏状态，并且评价的性能指标也不尽相同，仅凭单一子结构的破坏等级很难评定结构整体的破坏状态。本文假定各子结构之间呈串联关系，任一子结构的破坏都会导致结构整体的破坏。因此，结构整体的破坏状态通过各子结构的最大破坏状态来表示，即：

DSsystem=max{DS上部子结构,DS隔震层,DS下部子结构}

(8)

Nielson和DesRoches[11]将串联系统的易损性通过以下边界易损性来表示：

(9)

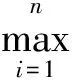
表6 层间隔震结构框架性能水平及量化指标限值

表7 框架结构破坏等级与量化指标的关系

隔震层和上、下部子结构分别采用隔震装置的位移、面压和层间位移角描述其性能指标，对应的性能水平及量化指标限值如表6所示。

根据我国普遍采用的结构破坏等级的划分方法[12]，结合表6中量化指标限值，将结构的破坏等级划分为表7中所示5种破坏等级。

3.3.2 易损性分析

结构地震易损性是指结构在不同地震动强度(IM)的激励下，发生不同破坏程度的可能性或结构达到某一极限状态的概率。为了得到给定IM下的超越概率，基于响应面分析结果，结合式(4)所示响应面分析模型，通过10 000次蒙特卡洛模拟，对不同IM下结构需求u超过限值LSi的概率表示为：

(10)

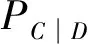
若层间隔震结构的各子结构之间相互独立，则最弱失效子结构的超越概率是式(9)中结构系统失效的下限；反之，结合各子结构超越概率可得到式(9)中结构系统失效概率的上限，如图8所示，根据结构系统的边界失效概率可以准确反应系统的易损性。

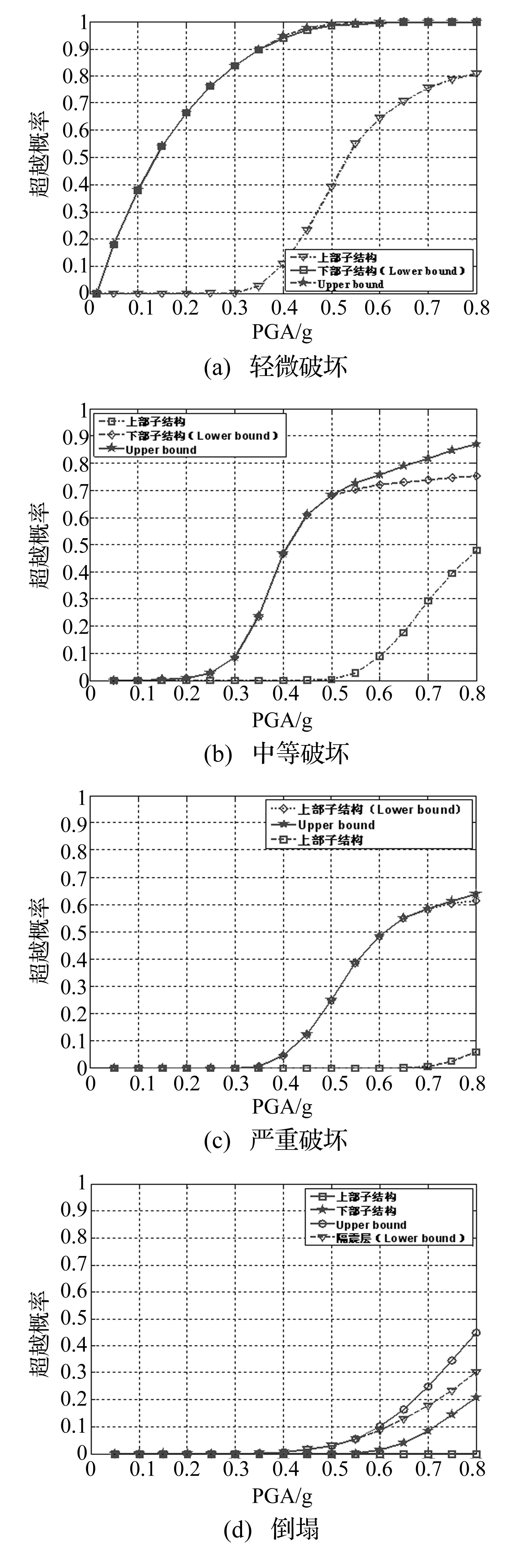
图8 层间隔震结构的易损性曲线

图8对比分析了各子结构及结构系统失效的界限超越概率，从图中可以看出，随着结构从轻微破坏到倒塌破坏，结构的易损性曲线逐渐变的扁平，即超越概率逐渐变小，其符合结构设计准则；无论在哪一种破坏等级下，层间隔震结构下部子结构的破坏概率大于上部子结构的破坏概率，随着破坏等级的加剧，上部子结构的破坏概率趋于0；结构系统易损性曲线的上、下边界较接近，表明结构系统的失效主要由最弱失效子结构控制，图8(a)所示上、下部子结构系统失效上、下边界几乎完全重合，系统的失效完全决定于下部子结构的失效，在图8(b)、(c)中，当PGA分别小于0.5 g、0.7 g时，上、下部子结构系统失效的上、下边界重合，PGA分别大于0.5 g、0.7 g时，其超越概率分别大于67.42%、58.64%，图8(d)所示为结构整体发生倒塌失效的易损性曲线，可以看出隔震层的失效概率大于下部子结构的失效概率，上部子结构的失效概率接近于0，当PGA小于0.56 g时，结构系统的失效由隔震层的失效控制。

4 结 论

本文提出了一种基于响应面法的层间隔震结构地震易损性分析方法，通过对一层间隔震结构进行易损性分析，得出以下结论：

(1) 提出的基于响应面法的层间隔震结构地震易损性分析方法计算量少、精度高，有效提高了易损性分析作为层间隔震结构性能评估的时效性；

(2) 地震动强度(PGA)对结构的影响大于混凝土抗压强度，钢筋抗拉强度和隔震支座屈服后刚度；

(3) 层间隔震结构下部子结构的破坏概率大于上部子结构的破坏概率，随着破坏等级的加剧，上部子结构的破坏概率趋于0，在结构倒塌破坏状态中，隔震层的失效概率大于下部子结构；

(4) 地震动强度PGA在不同范围内，结构系统的边界易损性曲线不同；在轻微破坏、中等破坏、严重破坏状态中，当PGA较小时，结构系统的失效主要是下部子结构控制；在同时考虑各子结构的倒塌破坏状态中，当PGA较小时，结构系统的失效由隔震层的失效控制；当PGA较大时，结构系统的失效由考虑各子结构相互依赖所得到的整体破坏状态控制，实际结构的易损性应位于两边界之间。

[1]Bucher C G, Bourgund U. A fast and efficient response surface approach for structural reliability problems[J]. Structural Safety, 1990, 7(1):57-66.

[2]Rajashekhar M R, Adidam S S R. Structural reliability analysis through response surfaces[J]. Journal of Structural Engineering, 1996, 22(4):179-192.

[3]刘晶波，刘阳冰，闫秋实,等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报，2010, 43(2)：39-47.

LIU Jing-bo, LIU Yang-bing, YAN Qiu-shi, et al. Performance-based seismic fragility of CFST frame structures[J]. China Civil Engineering Journal, 2010, 43(2): 39-47.

[4]吕大刚，于晓辉，潘峰,等. 基于改进云图法的结构概率地震需求分析[J]. 世界地震工程，2010, 26(1)：7-15.

LÜ Da-gang, YU Xiao-hui, PAN Feng, et al. Probabilistic seismic demand analysis of structures based on an improved cloud method[J]. 2010, 26(1): 7-15.

[5]吴子燕，王其昂，韩晖等. 基于响应面法的桥梁地震易损性分析研究[J]. 西北工业大学学报，2011, 29(1)：103-107.

WU Zi-yan, WANG Qi-ang, HAN Hui, et al. Applying RSM (Response Surface Methodology) to Making Seismic Analysis of Bridge More Effective, General and Practical[J]. Journal of Northwestern Polytechnical University, 2011,29(1): 103-107.

[6]吴巧云，朱宏平，樊剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学，2012, 29(9)：117-124.

WU Qiao-yun, ZHU Hong-ping, FAN Jian. Performance-based seismic fragility analysis of RC frame structures[J]. Engineering Mechannics, 2012, 29(9): 117-124.

[7]朱健. 结构动力学原理与地震易损性分析[M]. 北京: 科学出版社, 2013.

[8]Montgomery D C. Design and analysis of experiments (fifth edition). New York: John Wiley & Sons, Inc, 2001.

[9]Peeranan Towashiraporn. Building Seismic Fragilities using Response Surface Metamodels [D]. PhD Dissertation, Georgia Institute of Technology, 2004.

[10]Papila M, Haftka R T. Response surface approximations: noise, error repair, and modeling errors[J]. AIAA Journal, 2000, 12(38): 2336-2343.

[11]Nielson B G, Desroches R. Seismic fragility methodology for highway bridges using a component level approach[J]. Earthquake Eng Struct Dyn 2007,36:823 39.

[12]GB50011-2010建筑抗震设计规范[S].