高桩码头桩基检测信号分析中的反褶积应用
王元战,楚东堂,陈楠楠,邵 帅
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2. 厦门港口开发建设有限公司,厦门 361012)
桩基的无损检测是当今工程界的一个难题,有上部结构的梁板式高桩码头由于自身结构和所处环境的特殊性,具有更高的检测难度。
相比于单桩结构,梁板式高桩码头存在复杂的上部结构,整体呈现出明显的三维效应[1],当采用常用的低应变反射波法进行检测时,激振产生的应力波会产生大量的次生反射和干扰信号,加大了信号分析的难度。为此,国内相关研究人员在应力波传播机理和高桩码头检测方式上进行了一系列研究。彭志豪[2]通过数值模拟研究了高桩码头上部结构各构件尺寸对应力波传播的影响;季勇志[3]运用三维导波理论对高桩码头上部结构产生的三维效应问题进行了系统性的分析;张强等[4]对比了各种检测方式下的高桩码头桩基检测信号的清晰程度,并用小波分析对最佳信号进行了分析处理。但是,在目前的研究中,现有的桩基检测信号处理方法效果往往不尽人意。为了得到比较清晰的检测信号,多在检测操作上退而求其次,采用在桩身激振,桩身接收信号的方法,而高桩码头现场恶劣的自然环境和有限的检测空间会给这种检测操作带来相当大的难度。因此,对于梁板式高桩码头来说,找到一种方便、准确的检测和信号处理方法成为工程界亟待解决的难题。
在对勘探和检测领域的研究中我们发现,反射波法人工地震勘探和低应变反射波法桩基检测在检测原理和检测过程上具有较高的相似性[5]。由于人工地震勘探信号处理的相关理论研究较早,应用较为成熟,倪艳春等[6]曾尝试将反褶积的方法引入无上部结构的单桩基础桩基检测中,并取得了一定的效果。相比于单桩结构,梁板式高桩码头由于存在上部结构,其信号传播路径和地震勘探更为一致,其信号处理也更具有现实意义,因此本文尝试将反褶积方法引入低应变反射波法高桩码头桩基检测的信号处理当中。
1 反褶积法进行信号处理的原理
1.1 反褶积法在地震勘探中的求解思路
人工地震勘探是研究人工激发的弹性波在不同地层中传播规律的一种物探方法[7]。
在反射波法地震勘探中,由地表震源爆炸产生的尖脉冲以一维弹性波的形式在地层中传播,当传播到两个岩层分界面时,会形成反射波返回地面,完成地震信号检测过程。这样得到的地震记录可以表示为一个地层反射系数与地震波之间的褶积模型。假如没有震源附近介质对震源脉冲的改造作用,得到的地震记录应该是一系列尖脉冲。但是由于震源爆炸时岩石塑性圈等各种因素的干扰,使得震源发出的尖脉冲到达弹性形变区时变成了一个具有一定延续时间的地震子波b(t),干扰对震源脉冲的这种改造作用就相当于一个滤波器,地震记录也就变成了地震子波和反射系数序列的褶积。
为了使地震记录能够清晰的反映地下分层情况,我们希望在所得到的地震记录上,每个界面的反射波都能表现为一个尖脉冲,因此,反褶积的目的就是使模糊的地震记录还原为真实的反射系数序列ξ(t)。
假设地震记录x(t)为
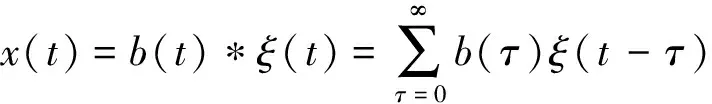
(1)
对式(1)两边求Fourier变换,可得在频率域上的地震记录表示式:
X(ω)=B(ω)·ξ(ω)
(2)
式(2)中的三个变量,从左到右依次为地震频谱、子波频谱和反射系数的频谱,如果让:
A(ω)=1/B(ω)
(3)
显然可以导出:
ξ(ω)=A(ω)·X(ω)
(4)
将式(4)做反Fourier变换至时间域可得:
ξ(t)=a(t)*x(t)=a(t)*b(t)*ξ(t)
(5)
在式(5)中,a(t)为A(ω)的时间函数,同时可以得出:
a(t)*b(t)=δ(t)
(6)
式中,δ(t)因为b(t)为地震子波,而a(t)和b(t)之间又存在着频谱互为倒数的关系,所以把a(t)称为反子波,又称为反褶积因子。
假如能够由子波求出反子波a(t),然后再将反子波a(t)与地震记录x(t)做褶积,就可以求出反射系数序列ξ(t),即:
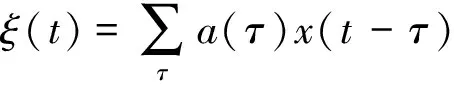
(7)
这样一个过程就叫做反褶积[8]。经过这样的处理,就可以达到提高地震记录纵向分辨能力的目的,这个过程可以通过下图形象的表示出来。

图1 反褶积过程的示意图
1.2 反褶积因子的求取原理
对于反褶积因子的求取,本文采用维纳反褶积的方法,其基本思想是设计一个滤波算子,用它把已知的输入信号转换为与给定的预期信号在最小平方误差的意义下是最佳接近的输出[9]。
先假设预期信号为窄脉冲d(t),在子波已知的情况下,设待求的反褶积因子a(t)起始时刻为-m0,延续长度为(m+1)。当已知地震子波b(t)时,实际输出与预期信号的误差平方和可以表示为:
(8)
为使误差平方和最小,可以通过求Q的极值的方法,得到满足下式的滤波因子a(t):
(l=-m0,-m0+1,…,-m0+m)
(9)
因为地震子波b(t)的自相关函数为:
(10)
而地震子波和预期信号的互相关函数为:
(11)
所以式(9)可以转化为:
rbb(l-τ)·a(l)=rbd(l)
(12)
该方程的系数矩阵为一种特殊的矩阵形式,被称之为托布利兹(Toeplitz)矩阵,其形式如式(13)所示:
(13)
由式(12)可知,只要已知地震子波b(t),求出其自相关函数rbb(t),带入矩阵运算即可求出反褶积因子a(t),用a(t)和地震记录x(t)褶积理论上即可得到压缩成尖脉冲的反射系数序列,即理想的地震记录,也就是地层反射系数序列ξ(t)。
a(t)*x(t)=a(t)*b(t)*ξ(t)≈ξ(t)
(14)
1.3 反褶积应用于桩基检测中的步骤
本文在利用反褶积进行桩基检测信号分析时,首先对原始信号进行预处理,变成零相位波形之后再进行反褶积,同时加hamming窗进行一次初始滤波,用Matlab进行数据处理。
整个信号处理过程如下:
(1) 在码头合适位置激振信号,选取合适的位置布置传感器,提取传感器接收到的速度时程曲线,分别作为桩身反射信号和子波信号的来源。
(2) 分别对桩身反射信号和子波进行波形零相位化和初始滤波,得到标准的桩身反射信号x(t)和子波信号b(t)。根据反褶积因子的求取原理,求得反褶积因子a(t),利用a(t)和桩身反射信号x(t)褶积得到经过反褶积处理之后的桩基检测信号。
(3) 经过反褶积处理之后的信号,在高频区域有时还会带有一部分剩余干扰信号,这种情况可对信号进行一次低通滤波处理。
2 有限元模型及参数确定
在低应变法检测桩基时,桩和土均处于线弹性变形阶段,所以在数值模拟中,码头桩基和桩周土均采用线弹性材料[10]。设置砂土和粘土两层土体,土体参数均按天津地区典型土壤的相关参数,见表1。
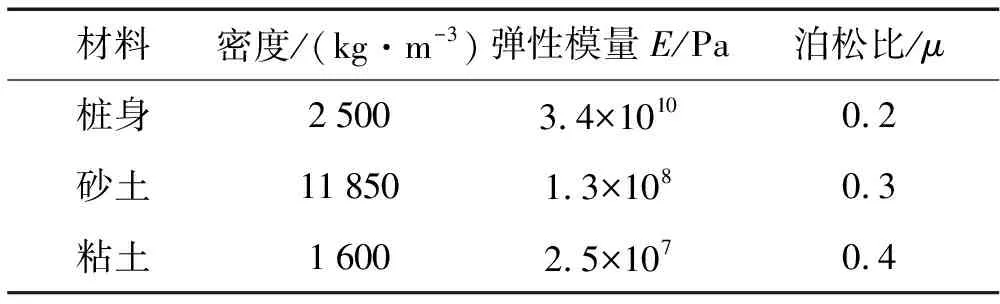
表1 桩、土材料参数
考虑相邻结构之间的相互影响,建立将纵梁、横梁、桩帽等上部结构固结为一体的群桩模型[11],共包含9根桩,按对称分布。按照《高桩码头设计与施工规范》中的相关规定确定群桩结构各部分的尺寸如下:
(1) 码头构件:桩基长度为30 m,横截面尺寸为0.45 m×0.45 m;桩帽高度为0.6 m,横截面尺寸为0.75 m×0.75 m;纵横梁顶面与地面等高,截面尺寸为0.45 m×1.2 m,面板厚度为0.5 m,横向排架间距3.5 m,前后桩距为3.6 m。
(2) 土体设置:土体上下表面和海面平齐,总厚度为20 m,其中砂土层在上,厚度为4 m,粘土厚度为16 m,粘土层纵向超过桩底4 m。
最终的有限元完整群桩模型如图2所示。

图2 梁板式高桩码头有限元模型
(3) 激振脉冲设置:激振点输入的瞬时纵向激振力采用升余弦脉冲来模拟[12]。
(15)
式中,T为激振脉冲作用时间,本文中取为2.0×10-3s,I为激振力冲量,取为0.06 N/s。
(4) 缺陷设置:对于缺陷桩,缺陷类型采用最常见的缩颈缺陷的形式,缺陷深度为0.2 m,为反映普遍情况,缺陷位置分别设置在桩顶以下10 m、15 m和20 m深度处。
3 高桩码头低应变检测的可行性分析
由于梁板式高桩码头整体性较好,利用低应变反射波法进行检测时,激振信号会发生弥散,使得最终检测结果存在不确定性因素。因此,首先要对低应变反射波法在梁板式高桩码头检测中的可行性和操作方式进行分析。
当在待测桩基正上方的面板表面激振信号时,利用数值分析读取激振信号在桩身的动态能量分布如图3所示。从图3中可以看出,激振信号在竖向传往待测桩的同时,会沿着码头上部结构进行横向传播,对检测信号产生干扰,但还是会有很大一部分激振能量通过竖向传播到达待测桩桩身,这部分能量碰到桩身波阻抗发生明显变化的部位,即桩身缺陷或者桩底时,即发生反射,被上部的传感器所接收,这就为利用低应变反射波法对梁板式高桩码头进行检测提供了可能。

图3 激振信号在码头中传播时的能量分布
为验证低应变反射波法在梁板式高桩码头中的可行性,以天津港某梁板式高桩码头的现场实测数据为例进行分析。该检测中采用的是PIT-X2型桩身完整性测试仪,在桩帽边缘激振信号,并在桩身侧面对检测信号进行接收。对于桩身基本完整的测试桩,得到的检测结果如图4所示。
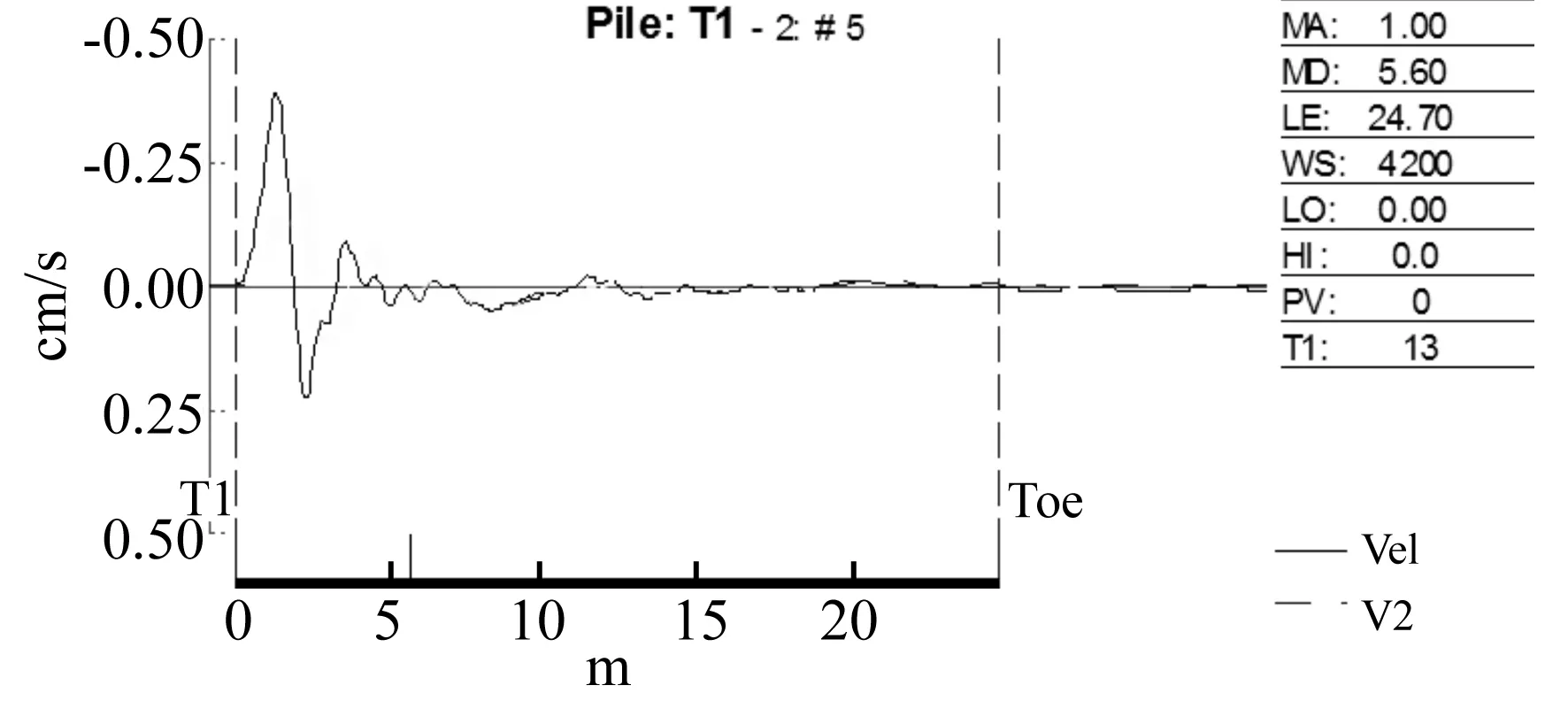
图4 某梁板式高桩码头的实测曲线
从图4中可以看出,当采用低应变反射波法对梁板式高桩码头进行桩基检测时,即使在非桩身的位置进行激振,也仍然能够得到比较完整的检测信号,信号特征和单桩结构检测结果较为一致。其主要问题为桩身反射信号较弱和干扰信号较多。所以,采用低应变反射波法进行梁板式高桩码头的检测是可行的。
同时,经过大量的数值模拟和现场实测结果可以得出,在码头不同位置激振和接收信号时,操作难度和信号清晰度的关系如图5所示。
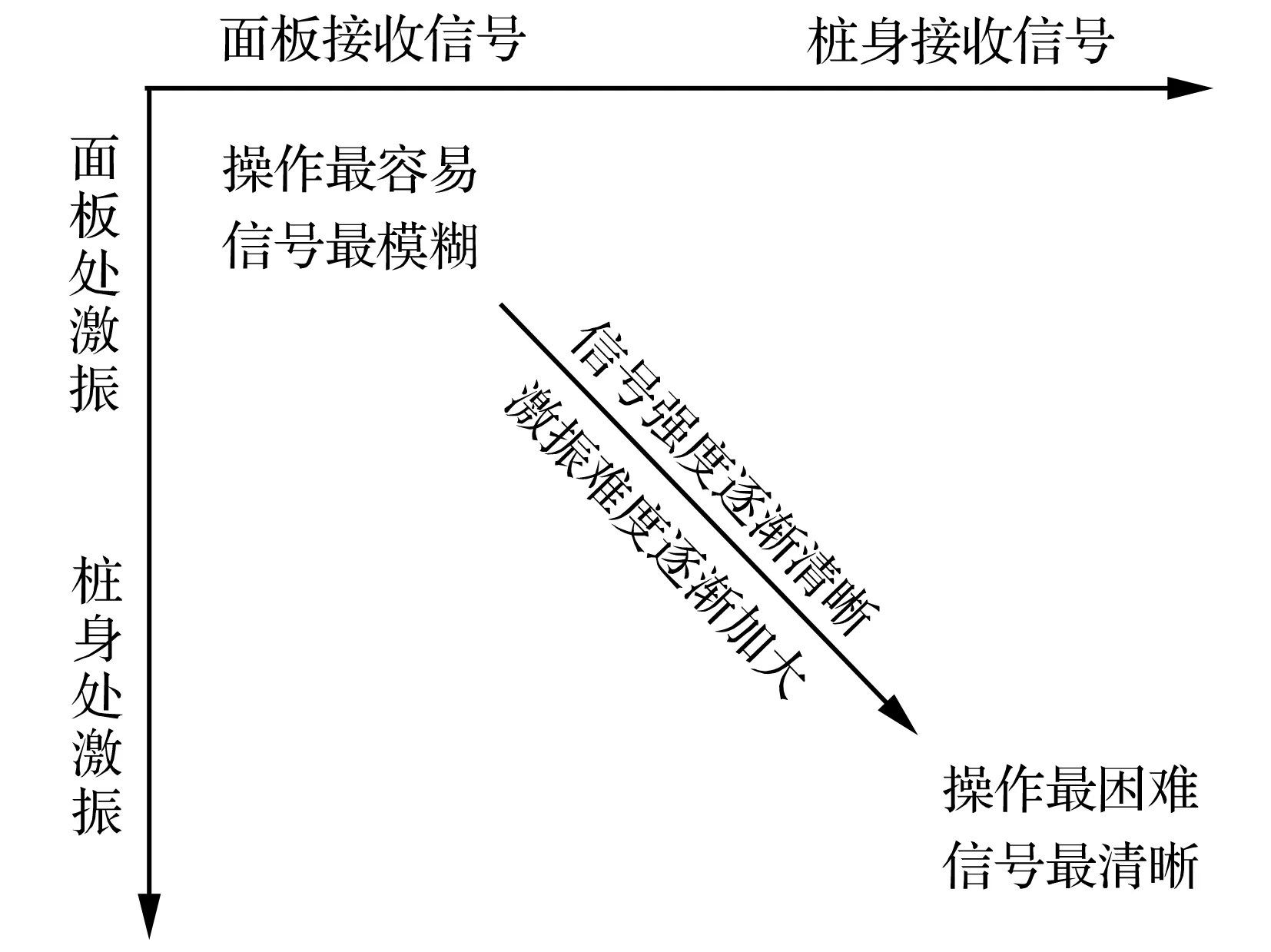
图5 高桩码头检测方式和信号清晰度的关系
从图5中可以看出,如果能够解决信号处理方面的难题,通过在面板上激振就能得到比较理想的结果,会大大减小实际检测的操作难度,本文主要研究这种检测方式,然后尝试利用反褶积方法解决信号清晰度的问题。同时,为了增加区分度和减少失误,可以对待测桩周围的桩基用同样的方法进行检测,以便于对比分析。
4 高桩码头桩基检测信号的反褶积分析
4.1 面板激振桩身接收信号
采用这种方式进行检测时,将激振点的位置选取在待测桩桩顶正上方的面板表面,在码头上安装两个传感器接收信号,第一个传感器安装在桩顶以下0.6 m的桩侧,用于接收桩身反射信号,第二个传感器安装在面板表面激振点附近,接收到的信号作为近似子波的来源。当不同深度处存在缺陷时,检测结果如下:
(1)桩顶以下20 m深度处存在缩颈缺陷
当桩顶以下20 m深度处存在缩颈缺陷时,桩顶以下0.6 m处的传感器接收到的原始桩身反射信号如图6所示。
从图6中可以看出,原始信号中干扰成分较多,且缺陷反射信号衰减严重,单从原始信号中无从判断缺陷信号和桩底反射信号,下面我们将其做反褶积处理,得到的结果如图7所示。
经过反褶积处理之后,可以清晰的分辨出缺陷反射和桩底反射的波形,读取各个反射波峰出现的时间节点,可得缺陷反射和首波峰反射之间的时间差Δt为0.010 57 s。
在本文所用的有限元模型中,桩身材料的弹性模量E为3.4×1010Pa,密度ρ为2500 kg/m3,根据一维纵波理论可得面板激发的弹性波在桩身的传播速度为:
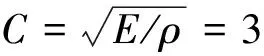
(16)
图6 桩身20 m处缩颈缺陷原始信号
由此计算缺陷深度得:
Δlc=0.5Δt×cs=19.491 m
(17)
在数值模拟中,传感器和缺陷位置的实际距离Δl为19.4 m,反褶积之后结果和理论值的相对误差为0.47%,与实际情况吻合良好。
(2)桩顶以下15 m深度处存在缩颈缺陷
当桩顶以下15 m深度处存在缩颈缺陷时,桩顶以下0.6 m处的传感器接收到的原始桩身反射信号如图8所示。
从图8中,同样不能准确判定缺陷位置,对其做反褶积处理之后,得到的结果如图9所示:
经过反褶积处理之后,可以清晰的看到在桩身15 m深度处存在一个完整的缺陷反射波形,缺陷反射和首波峰反射之间的时间差Δt为0.007 7 s,计算得到的缺陷深度为14.20 m,与理论值的相对误差为1.40%,与实际情况吻合较好。
(3)桩顶以下10 m深度处存在缩颈缺陷
当桩顶以下10 m深度处存在缩颈缺陷时,桩身原始反射信号如图10所示。
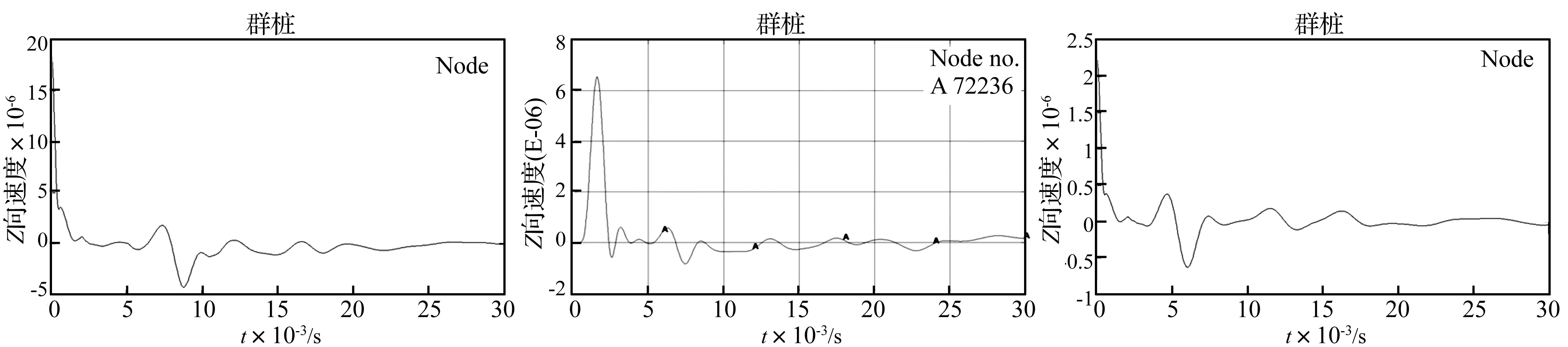
图9 反褶积处理后信号
从图10中,已经可以看到一个疑似缺陷反射波形,但是干扰信号较多。计算缺陷反射波峰位置和首波峰反射位置的时间差可得Δt为0.004 86 s,计算得到的缺陷深度为8.973 m,与理论值9.4 m的相对误差为4.54%,也从侧面验证了当采用低应变反射波法进行群桩结构高桩码头桩基检测时,由于反射波法本身的限制和上部结构的影响,桩基浅部缺陷的检测精度会受到影响。
下面对其做反褶积处理,得到的结果如图11所示。从反褶积的结果可见,经过反褶积处理之后,缺陷反射的波形变得很清晰,但桩底反射的波形不太明显,同时对桩身后半段干扰信号的压制效果减弱,反褶积之后缺陷位置的计算结果和实际情况的相对误差为3.87%。
对比以上三种深度处缺陷桩的数值模拟分析结果可以发现,当采用面板激振,桩身接收信号的方法时,缺陷深度越深,缺陷反射的信号衰减越严重,当桩基深部存在缺陷时,通过原始信号完全不能分辨出缺陷位置。对原始信号进行反褶积处理之后,可以一定程度上还原桩身真实情况,而且缺陷深度越深,反褶积处理的效果越明显,计算结果精确度越高。
4.2 面板激振面板接收信号
下面,我们尝试检测操作最为方便,但是信号处理难度最高的一种检测方法,即在桩身正上方的面板激振信号同时在面板接收检测信号的方法。
当采用这种形式检测时,在面板上激发的应力波在向下传播的同时也会沿着面板和纵横梁横向传播,遇到界面即反射回来,叠加在激振位置附近。反映在最终的检测结果中就是,无论完整桩还是缺陷桩,在面板上接收到的信号从波形上看应该是基本相同的,数值模拟结果也验证了这种推论,分析结果如图12所示。
图12中的四个波形分别是桩身完整,桩身10 m深度处、15 m深度处、20 m深度处存在缩颈缺陷的桩身反射信号。可以清晰的发现四个图的波形基本一致,无从辨别缺陷信号。
下面,我们尝试利用反褶积方法进行信号处理,以求得到桩身真实情况。对于子波的提取,首先依然采用在激振点附近提取信号作为近似子波的方法。经过多次尝试发现,采用这种形式的子波得到的反褶积结果不太稳定,计算得到的缺陷反射曲线存在较大变形,计算精度不高。
为了得到比较精确的结果,我们需要找到一个更加合理的子波。根据反褶积方法的原理,我们尝试模拟完整桩的桩身反射信号,利用其作为这种情况下反褶积信号处理的公用子波。
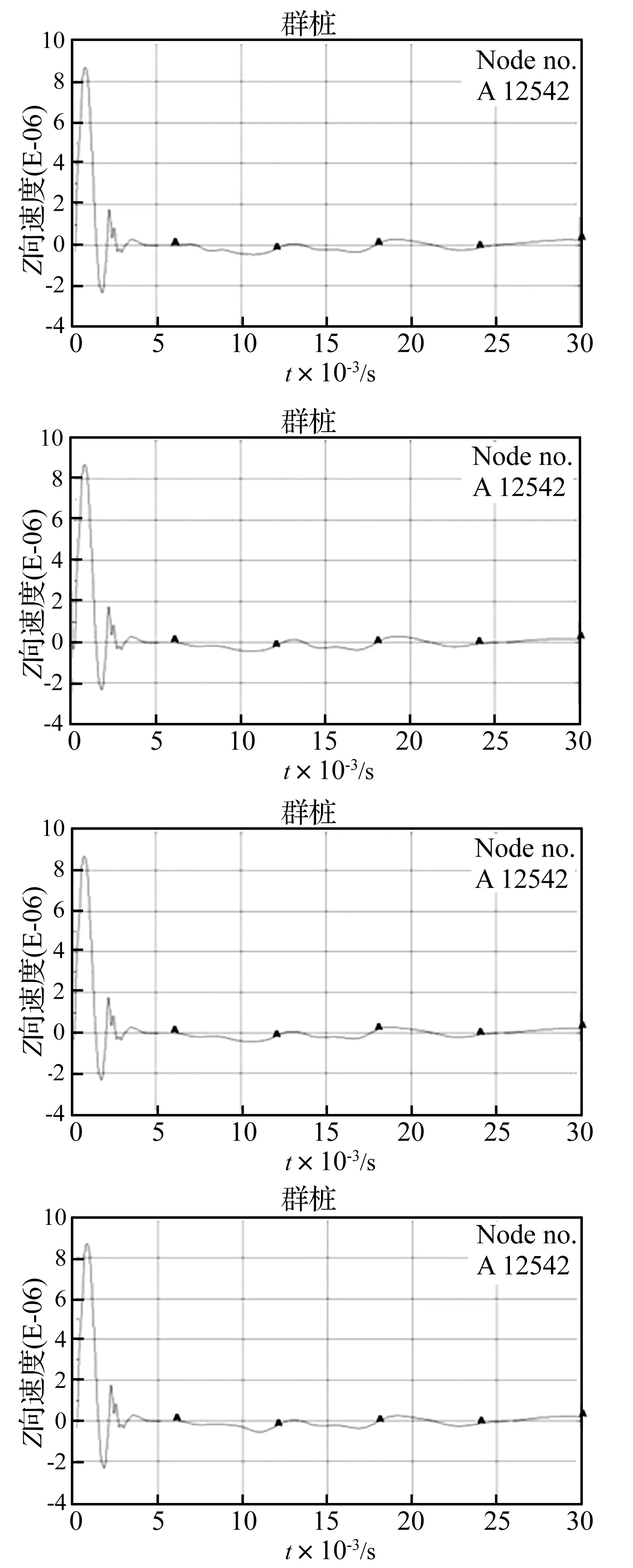
图12 不同深度处存在缺陷时面板接收信号
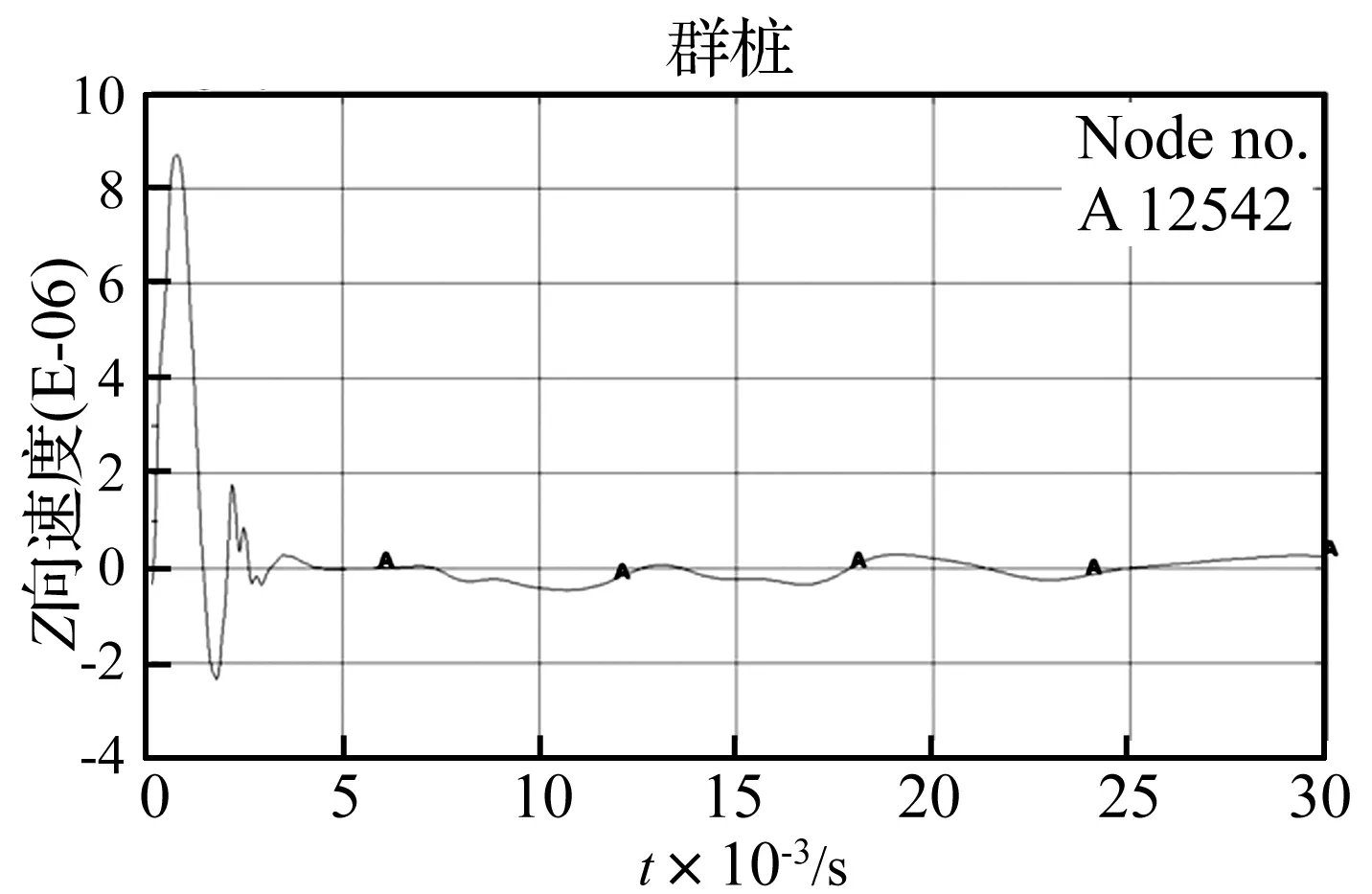
图13 桩顶以下10 m处缺陷原始信号
在目前的研究中,已经有部分学者对模拟完整桩的桩身反射信号来解决桩基检测问题的思路进行了一些研究。天津大学的季勇志曾经提出模拟完整桩信号,从中分离出干扰信号,之后将实际桩基检测结果消减掉之前得到的干扰信号以期尽量排除干扰的检测方法[13],在有上部结构的单桩结构中,取得了不错的效果。但是,在群桩码头中,特别是对于面板激振面板接收信号的检测方式,经过多次数值模拟尝试,直接采用这种信号分离的方法得到的结果干扰信号依旧较多,而且实际操作中,这种分离干扰信号的方法对模拟信号的精度要求很高,所以分离干扰信号的方法在群桩结构中并不适用。但是,模拟完整桩的桩身反射信号作为反褶积的公用子波可以为解决信号处理的问题提供一个很好的思路。当不同深度处存在缺陷时,用完整桩的桩身反射模拟信号作为公用子波得到的反褶积分析结果如下:
(1)桩顶以下10 m深度处存在缩颈缺陷
当桩身10 m深度处存在缩颈缺陷时,在面板激振,面板接收得到的原始信号如图13所示。
从图12中的对比分析中已经得出,单从面板接收到的原始信号中已经看不出任何缺陷反射信号的迹象,必须借助于其他处理方式对其进行分析。下面利用公用子波得到的反褶积因子对其做反褶积处理,得到的结果如图14所示。
图14 反褶积处理后的信号
从反褶积处理之后的结果中,可以清晰的看出桩身10 m处存在一个明显的缺陷反射波形,计算得到的缺陷深度为12.02 m。因为在面板表面接收信号时,实际缺陷位置距离传感器的距离为12.3 m,所以反褶积之后得到的结果和实际深度的相对误差为2.27%,与实际情况吻合较好。
(2)桩顶以下15 m深度处存在缩颈缺陷
当桩顶以下15 m深度处存在缩颈缺陷时,在面板激振,面板接收得到的原始信号波形曲线同图13类似,这里不再赘附。利用公用子波得到的反褶积因子对原始桩身反射信号做反褶积处理,得到的结果如图15所示。
从反褶积处理之后的结果中,可以清晰的看出桩身15 m处存在一个明显的缺陷反射波形,第二个反射波形的凹陷处为桩底反射的位置。计算缺陷反射位置得到的结果和实际缺陷深度的相对误差为0.94%,与实际情况吻合良好。
(3)桩顶以下20 m深度处存在缩颈缺陷
当桩身20 m处存在缩颈缺陷时,利用公用子波得到的反褶积因子对原始桩身反射信号做反褶积处理,得到的结果如图16所示。
从反褶积处理之后的结果中,可以清晰的看出桩身20 m处存在一个明显的缺陷反射波形,经计算得到的结果和实际深度的相对误差为0.53%,与实际情况吻合良好。
通过对各个深度处存在缺陷时,面板激振面板接收信号的反褶积分析可以看出,提取公用子波对测桩信号进行反褶积处理的方法可以很好的解决信号清晰度的问题。
5 结 论
本文首次将反褶积方法应用于梁板式高桩码头桩基检测信号处理当中,分别建立了桩基在不同深度处存在缺陷的有限元模型进行数值分析,验证了反褶积方法在高桩码头桩基检测信号处理中的适用性,并得出了以下结论:
(1) 当采用面板激振的形式进行高桩码头的桩基低应变检测时,检测操作较为方便,但上部结构对信号的干扰严重,缺陷信号不能有效识别,尤其对于深层缺陷,缺陷信号衰减非常厉害,需要开展相关信号分析的研究。
(2) 当在桩身上接收桩身反射信号时,可以将面板激振点附近接收到的桩身反射信号预处理之后作为近似子波,利用反褶积方法对测桩信号进行处理,可以在一定程度上还原桩身实际情况,滤除上部结构的干扰。
(3) 反褶积方法对于深层缺陷反射信号的分析效果最明显,结果最准确,对于浅层缺陷,受限于低应变反射波法本身在浅部缺陷检测上的局限和群桩上部结构三维效应的影响,检测精度下降。
(4) 当采用在高桩码头面板激振面板接收信号的形式检测时,不同缺陷情况得到的原始桩身反射信号基本一致,这是因为干扰信号叠加在激振位置附近,其强度远大于从桩身传播上来的缺陷反射信号。
(5) 当采用面板激振面板接收信号时,采用模拟完整桩的面板接收信号作为公用子波的方法进行反褶积信号处理可以得到比较理想的结果。考虑正在服役的高桩码头完整桩信号的模拟存在难度,可以在码头刚建好之后,提取一根完整桩的桩身反射信号存档,作为以后检测时的子波来源。
综上可得,反褶积方法在高桩码头桩基低应变检测的信号处理中是一种不错的思路,可以在一定程度上还原桩身实际情况。同时,反褶积有很多种计算方法,将其引入桩基检测信号处理中时,在具体实现过程上还带有一定的尝试性,在本文中,采用的是波形零相位化和纯振幅维纳反褶积两个步骤来实现的,后续可以开展其他反褶积实现方法在桩基检测中的应用分析。
[1]孙熙平,王元战,徐满意. 高桩码头基桩完整性检测技术研究综述[J]. 港工技术,2010,47(2):50-53.
SUN Xi-ping, WANG Yuan-zhan, XU Man-yi. Research summary of integrity detection for High-piled wharf pile[J]. Port Engineering Technology,2010,47(2):50-53.
[2]彭志豪. 高桩码头在役桩基完整性检测方法的研究[D]. 天津:天津大学,2009.
[3]季勇志. 基于三维导波理论的码头桩基无损检测方法的数值模拟研究[D]. 天津:天津大学,2010.
[4]张强,孙熙平,王元战. 高桩码头基桩完整性检测技术研究[J]. 港工技术,2010,47(6):52-56.
ZHANG Qiang, SUN Xi-ping, WANG Yuan-zhan. Study of integrity detection technique for piles foundation of piled wharf[J]. Port Engineering Technology,2010,47(6):52-56.
[5]倪艳春,凡友华,袁大器. 反褶积对桩基础低应变检测适用范围的验证[J]. 水运工程,2009(3):24-30.
NI Yan-chun, FAN You-hua, YUAN Da-qi. Application of uniform design method for determining the applicable scope of deconvolution in low strain integrity testing of pile foundation[J]. Port & Waterway Engineering,2009(3):24-30.
[6]倪艳春,凡友华,袁大器. 反褶积在桩基低应变检测中的应用分析[J]. 建筑科学,2009,25(1):19-22.
NI Yan-chun, FAN You-hua, YUAN Da-qi. The application of deconvolution in low strain integrity testing of the pile[J]. Building Science,2009,25(1):19-22.
[7]马海波. 物探技术及岩性地震勘探技术分析[J]. 科技与企业,2012(7):172.
MA Hai-bo. Geophysical and lithologic seismic exploration technical analysis. Science and technology & Enterprises,2012(7):172.
[8]姚姚. 地震波场与地震勘探[M]. 北京:地质出版社,2006.
[9]牟永光. 地震勘探资料数字处理方法[M]. 北京:石油工业出版社,1981.
[10]Kasali G,Lemke J, Jabakhanji R,et al. Finite element model of dynamic pile test using embedded transducers[C]. GeoCongress,2006.
[11]Cairo R, Conte E, Dente G. Analysis of pile groups under vertical harmonic vibration[J]. Computers and Geotechnics, 2005, (32),545-554.
[12]季勇志,王元战. 基于ANSYS/LS-DYNA的码头基桩完整性检测的数值模拟和方法研究[J]. 振动与冲击,2010,29(2):199-201.
JI Yong-zhi, WANG Yuan-zhan. The numerical simulation of integrity detection technique for piles foundation of piled wharf based on ANSYS/LS-DYNA[J]. Journal of Vibration and Shock,2010,29(2):199-201.
[13]季勇志,王元战,王立强. 码头混凝土桩无损检测数值研究[J]. 北京工业大学学报,2011,37(11):1729-1732.
JI Yong-zhi, WANG Yuan-zhan, WANG Li-qiang. The Numerical Study on non-destructive methods of concrete pile integrity of wharf[J]. Journal of Beijing University of Technology,2011,37(11):1729-1732.

