单支撑1000MW超超临界汽轮机轴系不平衡响应分析

高庆水，邓小文，张 楚，刘 石，杨建刚

(1.广东电网公司 电力科学研究院,广州 510080；2.东南大学 火电机组振动国家工程研究中心,南京 210096)

1 000 MW超超临界汽轮机为目前世界先进汽轮发电机组[1]。上海电气集团引进德国西门子技术制造的1 000 MW汽轮机组由高压、中压及两低压转子组成，所用单支撑结构见图1，N个转子由N+1个轴承支撑，具有结构紧凑、轴承数少、稳定性高等优点。该机组投运后出现的不稳定振动[2-7]，影响机组安全运行，其轴系动力学问题须引起重视。因大容量、单支撑汽轮机同型机组较少，对其轴系动力特性认识并不深入。诸多研究认为单支撑1 000 MW汽轮机减少3个轴承，所测振动仅为转子单侧信号，不能完全反映转子振动特性，无法判别转子振型，故障诊断困难[3-5]。单支撑轴系相邻转子振动相互影响较大，轴系动平衡工作难度较大，需综合考虑动平衡对相邻转子影响[5-8]。

图1 西门子型1 000 MW机组轴系布置图

本文建立单支撑1 000 MW汽轮机动力学模型，分析轴系不平衡响应特性，并在某台1 000 MW机组上开展动平衡试验。所得单支撑机组不平衡响应规律可指导机组进行轴系动平衡，提高动平衡效率。

1 轴系动力学分析模型

1.1 轴段模型

图1为1 000 MW汽轮机简化后的动力学模型,共含271个轴段、64个集中质量和5个轴承，转子总重243.34 t，总长27.35 m，见图2。

图2 轴系动力学分析模型

1.2 轴承载荷求解模型

图3 轴段分解模型

求解轴承动力特性系数之前，必须首先求出轴承载荷。在中间3个轴承处将轴断开，将轴系拆成如图3所示4个轴段。对于由第i和i+1个轴承所组成的轴段i而言，由传递矩阵理论可知[8]

(1)

式中，y,θ,M,Q为截面位移、转角、弯矩、剪力;上标R,L分别代表轴段右、左侧;Ti为第i个轴段状态参数传递矩阵[8]。第i-1个轴段和第i个轴段之间轴承的支反力Fi为

(2)

两端边界条件为

(3)

给定轴承标高后，由上述方程组即可以求出轴承反力。表1为给定标高下计算所得轴承载荷值。

表1 轴承标高和载荷

1.3 轴承动力特性分析

图4为轴承分析模型。滑动轴承静态压力和扰动压力Reynolds方程为

图4 滑动轴承求解模型

(4)

式中:φ为方位角;l为宽度;H为膜厚;e为偏心率;c为轴承间隙;ε为偏心率。边界条件为

(5)

采用有限差分法求解静态及扰动压力雷诺方程，积分后得到轴承动力特性系数。

1.4 转子-轴承系统不平衡响应计算模型

转子-轴承系统动力学方程为

(6)

式中:ω为旋转频率;M1,K1,G1为整体质量矩阵、刚度矩阵和回转矩阵[8];cij,kij(i,j=1,2)为整体油膜等效阻尼和刚度矩阵;U1,2为系统位移向量,即

U1={x1θy1x2θy2…xnθyn}T

U2={y1-θx1y2-θx2…yn-θxn}T

Q为不平衡力向量,即

(7)

Qc,s为不平衡力向量中余弦和正弦分量值。设

(8)

式中:A1,2,B1,2为不平衡响应中余弦和正弦量值。

将式(7)、(8)代入式(6)，得

(9)

式中:

1.5 不平衡力

汽轮机转子三阶临界转速远高于工作转速，不平衡响应分析可以只考虑前两阶模态影响。计算时在转子两端叶轮处各设置一组力偶和一组力，分别模拟二阶模态和一阶模态影响。不平衡位于图1中G1/G2、G3/G4、G5/G7和G8/G10平面。

2 汽轮机不平衡响应特性计算

垂直和水平振动特性相似，现以垂直振动为例进行分析。图5～图8给出了4根转子升速过程中的不平衡响应，上、下2个图分别对应着不平衡力和力偶作用。

2.1 高压转子不平衡响应特性分析

高压转子一阶临界转速(2 600 r/min)距离工作转速(3 000 r/min)较近，升速以及3 000 r/min下不平衡力影响远大于力偶影响。转子结构不对称导致#1、#2轴承振幅不等，不平衡力偶作用下，在一阶临界转速2 600 r/min处也出现了振动峰值。受中压转子临界转速影响，1 900～2 600 r/min区间内#2轴承振动较大，共振区域较宽。

工作转速下#1、#2轴承振动最大，#3轴承振动其次。不平衡力作用下两侧轴承振动相位相近，升速过程中相位从30°变化到180°。不平衡力偶作用下#1、#2轴承振动相位近似相反，升速过程中相位从30°变化到130°。

2.2 中压转子不平衡响应特性分析

中压转子临界转速为2 000 r/min。不平衡对高/中压转子振动都产生了较大影响。由于高中压转子振动耦联，升速过程中#1～#3轴承共振区较宽。

中压转子在不平衡力作用下，#2、#3轴承振动相位相近，升速过程中从30°变化到270°。在不平衡力偶作用下，#2、#3轴承振动相位近似相反，从30°变化到170°。

图5 高压转子不平衡响应特性

图6 中压转子不平衡响应

2.3 低压转子不平衡响应特性分析

2根低压转子的一阶临界转速分别为1 100 r/min和1 150 r/min。如图7和图8所示，2根低压转子不平衡响应特性类似，现以低压Ⅱ转子为例进行分析。

随着转速升高，不平衡力偶所起作用增大，工作转速下振动受力偶影响较大。临界转速处，低压Ⅱ转子不平衡对2根低压转子振动都产生了较大影响。在低压I转子临界转速处，#4、#5轴承相位出现不规则突变。该转速之后，相位逐渐恢复正常。

不平衡力作用下，两侧轴承振动相位相近，临界转速处相位变化明显，升速过程中相位从30°变化到290°。不平衡力偶作用下，两侧振动相位近似相反，升速过程中从30°逐步变化到160°。

图7 低压转子Ⅰ不平衡响应特性

图8 低压转子Ⅱ不平衡响应特性

2.4 单支撑汽轮机不平衡响应特性总结

由前面分析可知，单支撑汽轮机轴系不平衡响应和传统双支撑汽轮机相似，振动分析时可以把两侧两个单支撑看作为该转子的双支撑，由这两个轴承振动来分析不平衡面和不平衡型式。

单支撑/双支撑汽轮机不平衡响应差异主要表现在：

(1) 单支撑汽轮机相邻转子振动耦联较强，特别是在临界转速附近。在不平衡转子临界转速附近，相邻转子振动会被激发出来；相邻转子临界转速附近，不平衡所在转子振动同样会被激发出来。该转速附近，相位还有可能出现不规则变化。通过该转速后，相位逐步恢复正常。

(2) 该机型工作转速远低于转子二阶临界转速，由振动理论可知，工作转速下振动与不平衡力偶之间的滞后角应该小于90°。但是实际计算结果表明，工作转速下单支撑汽轮机不平衡力偶所引起的振动相位大多在120°以上。振动与力之间的相位差(滞后角)对于合理确定动平衡试加重角度很重要。

3 1 000 MW单支撑汽轮机动平衡试验

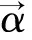
(10)

由此计算出的影响系数反映了在转子两端加1kg∠0°和1kg∠180°后的振动响应。

图9给出了低压Ⅱ转子两端加不平衡力偶后的振动响应。随着转速的升高，不平衡力偶所起作用逐渐增大。虽然工作转速远低于二阶临界转速，但工作转速下不平衡力偶所引起的振动滞后角达到了135°。动平衡试验结果与计算结果基本吻合。由于滞后角选取准确，经过一次动平衡即取得了明显的减振效果。

表2 低压转子Ⅱ动平衡前后振动数据

图9 低压Ⅱ转子两端加不平衡力偶后的振动响应

4 结 论

(1) 单支撑汽轮机相邻转子之间振动耦联性较强，突出表现在两个转子临界转速附近，共振区域较宽。临界转速距离工作转速较远时，转子之间的相互影响并不是很大。分析单支撑汽轮机不平衡响应特性时，可以把转子两侧两个单支撑轴承看作为该转子的双支撑。

(2) 通过相邻转子临界转速时，不平衡所在转子的振动相位有可能会出现不规则变化，其后相位又会逐步恢复正常。

(3) 虽然二阶临界转速高于工作转速，但是单支撑机组不平衡力偶作用下的振动相位大多在120°以上，该现象也得到了试验证实。

(4) 不平衡响应计算结果与动平衡试验结果吻合较好。

[1] 何阿平,彭泽瑛.上汽-西门子型百万千瓦超超临界汽轮机[J].热力透平,2006,35(1):1-8.

HE A-ping, PENG Ze-ying.Ultra supercritical 1000MW steam turbine designed by STC and siemens[J].Thermal Turbine,2006,35(1):1-8.

[2] 吴文健,童小忠,应光耀,等.单支撑超超临界1000MW汽轮发电机组振动诊断及处理[J].浙江电力,2011(10):32-36.

WU Wen-jian, TONG Xiao-zhong, YING Guang-yao, et al.Diagnosis and treatment of ultra supercritical 1000MW steam turbine units supported by single bearing[J].Zhejiang Electric Power, 2011(10):32-36.

[3] 韩彦广,周雪斌,李旭,等.上汽西门子1000MW超超临界汽轮发电机组轴系振动特性[J].湖南电力,2010,30(增刊):60-64.

HAN Yan-guang, ZHOU Xue-bin, LI Xu, et al.Characteristics of shaft system vibration of siemens for 1000MW ultra supercritical steam units[J].Hunan Electric Power,2010,30(S):60-64.

[4] 陈建县.1000MW超超临界机组汽轮机轴瓦振动原因分析及处理方法[J].华东电力, 2010,38(3):421-424.

CHEN Jian-xian.Analysis of vibration cause for turbine bearing bush in 1000MW ultra-supercritical unit and its treatment method[J].East China Electric Power,2010, 38(3):421-424.

[5] 应光耀,吴文健,童小忠,等.1000MW汽轮发电机组不稳定振动故障诊断及治理[J].浙江电力,2011(7):38-40.

YING Guan-yao, WU Wen-jian, TONG Xiao-zhong, et al.Fault diagnosis and treatment of unstable vibration of 1000MW ultra supercritical steam turbine generator unit bearing[J].Zhejiang Electric Power, 2011(7): 38-40.

[6] 张学延,张卫军,葛祥,等.西门子技术1000MW超超临界机组轴系振动问题[J].中国电力,2012,45(5):68-73.

ZHANG Xue-yan, ZHANG Wei-jun, GE Xiang, et al.Vibration of turbine shafting in 1000MW ultra supercritical unit with Siemens technology[J].Electric Power, 2012,45(5):68-73.

[7] 宾光富,何立东,高金吉,等.基于模态振型分析的大型汽轮机低压转子高速动平衡方法[J].振动与冲击,2013,32(14):87-92.

BIN Guang-fu,HE Li-dong,GAO Jin-ji,et al.High-speeddynamic balancing method for low pressure rotor of a large steam turbine based on modal shape analysis[J] Journal of Vibration and Shock,2013,32(14):87-92.

[8] 钟一谔，何衍宗，王正，等.转子动力学[M].北京：清华大学出版社，1987.