线控转向系统对汽车操纵稳定性的影响
于蕾艳,金 涛,伊剑波,鲍长勇,郑亚军
(中国石油大学(华东) 机电工程学院,山东青岛 266580)
线控转向系统对汽车操纵稳定性的影响
于蕾艳,金 涛,伊剑波,鲍长勇,郑亚军
(中国石油大学(华东) 机电工程学院,山东青岛 266580)
基于MATLAB/Simulink软件建立线控转向系统的动力学模型,分析线控转向系统关键部件——转向电机的转动惯量、阻尼系数、刚度等对汽车操纵稳定性的影响。合理设计线控转向系统转向电机的结构参数,可提高汽车的操纵稳定性。
线控转向系统;操纵稳定性;转向电机;参数;动力学模型
汽车线控转向系统(steer by wire system,SBW)采用电机实现前轮转向,响应快速,可提高汽车的操纵稳定性[1-4]。汽车线控转向系统的动力学模型是研究控制算法的基础[5-7]。若采用线性二自由度整车模型,不能较好的反映大轮胎侧偏角时的特性[8-10]。本文首先建立线控转向系统的动力学模型,采用基于魔术公式的轮胎模型,分析线控转向系统的结构参数对汽车操纵稳定性的影响。
1 线控转向系统动力学模型
1.1线控转向系统的动力学模型框图
基于MATLAB/Simulink软件建立包括线控转向系统、整车、驾驶员等的人-车-路闭环系统动力学模型,如图1所示。
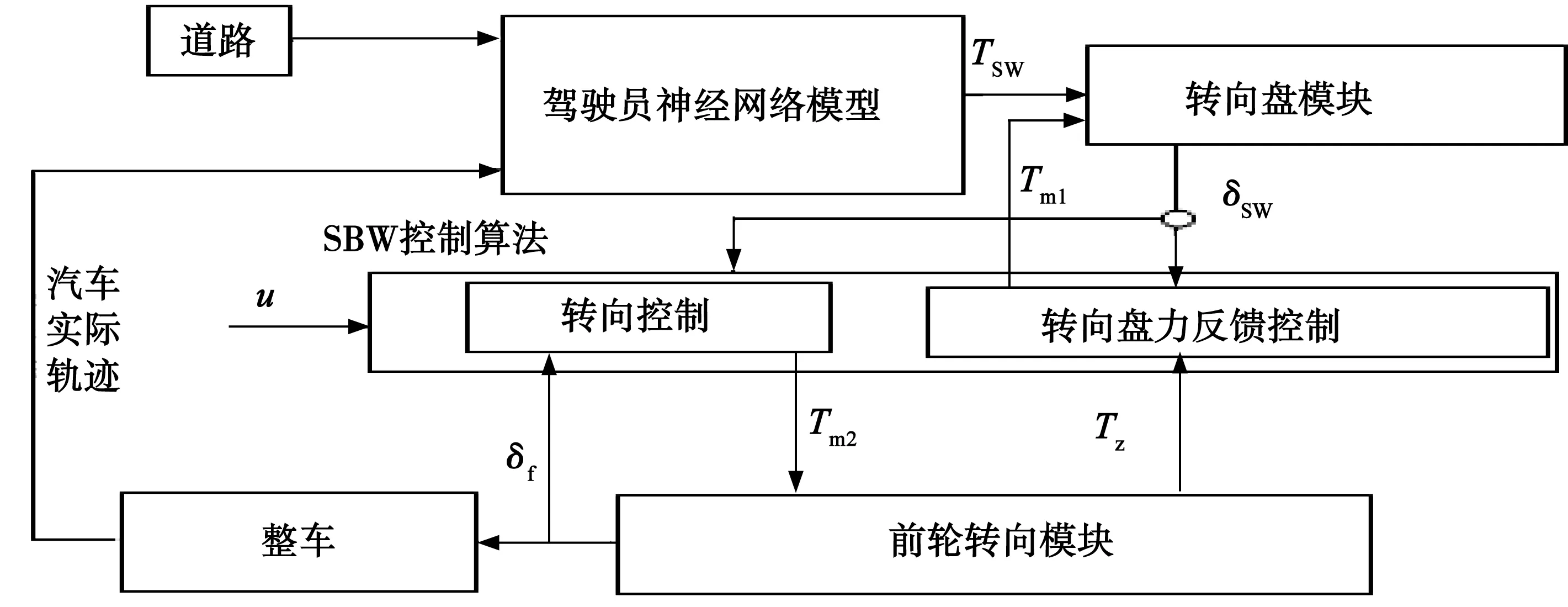
图1 人-车-路闭环系统动力学模型框图
图1中,驾驶员模型采用神经网络模型,基于目标道路轨迹与实际道路轨迹的偏差对转向盘施加转向盘力矩Tsw。SBW控制器根据车速u、前轮转向模块轮胎回正力矩Tz由转向盘力反馈控制算法对转向盘施加转向盘阻力矩Tm1,反映轮胎转向阻力矩的作用。SBW控制器的转向控制算法根据车速u、转向盘转角δsw等信息向前轮转向模块的前轮转向电机提供控制信号,转向电机力矩Tm2驱动转向器、前轮转向组件动作,得到前轮转向角度δf。δf输入整车模型,得到整车横摆角速度及汽车实际轨迹等,汽车实际轨迹反馈至驾驶员模型,构成闭环反馈[11-12]。
1.2转向盘模块动力学模型
转向盘模块是线控转向系统的重要人机界面,驾驶员通过转向盘转角发出转向指令,通过转向盘力矩得到适当的路感。对于转向盘模块,主要考虑转向柱、转向盘力反馈电机(转动惯量为Jm1,阻尼系数为bm1)的动力学特性。图2为转向盘模块动力学模型,驾驶员输入给转向盘一个力矩Tsw时,转向盘力反馈电机施加力矩Tm1,通过电机减速器(速比nm1)提供转向盘阻力矩,实现一定的转向盘转角。

图2 转向盘模块动力学模型
1.3转向模块动力学模型
图3为转向模块的动力学模型,主要考虑了转向电机、齿条、前轮共3个二阶运动微分方程[6]。输入为转向电机力矩Tm2、轮胎回正力矩Tz,状态变量为转向电机转角、齿条位移、前轮转角δf,输出为δf。图3中,Jm2为转向电机的转动惯量,bm2为转向电机的阻尼系数,km2为转向电机的刚度,nm2为转向电机减速器的速比,rP为齿轮齿条型转向器的小齿轮半径,Jw为前轮转动惯量,bkp为主销阻尼系数,rL为主销轴的偏距,kL为转向拉杆刚度,mr为齿条质量,br为齿条阻尼系数。

图3 转向模块动力学模型
1.4轮胎模型
整车模型采用非线性三自由度整车模型,包括质心侧偏角、整车横摆角速度和车身侧倾角3个状态变量。采用魔术公式[13]型轮胎回正力矩模型计算Tz,计算公式为
Tz=Dsin{Carctan[Bα-E(Bα-arctan(Bα))]},
(1)

图4 Tz与α、Fz的关系
式中α为轮胎侧偏角;C为曲线形状因子,C=2.4;D为峰值因子,D=a1Fz2+a2Fz,其中Fz为轮胎法向负荷;B为刚度因子,B=BCD/(CD),其中BCD=(a3Fz2+a4Fz)/ ea5 Fz;E为曲线因子,E=a6Fz2+a7Fz+a8,a1~a8为拟合系数。
图4显示了Tz与α、Fz的三维关系。一定的Fz下,Tz的变化分为3个阶段。在小α范围内,Tz随α增加而非线性增加;α超过一定数值后,Tz随α增加而非线性减小,而后,Tz改变方向,随α增加而增加。采用魔术公式轮胎模型建立的三自由度整车模型可较好的反映整个转向过程中的动力学特性。
1.5线控转向系统的PID控制器模型
线控转向系统控制包括上层控制和下层控制。对于下层控制,转向电机采用经典的PID控制[14-16],以使实际前轮转角跟踪前轮目标转角。图5中,δf*为前轮目标转向角,kP为比例系数,kI为积分系数,kD为微分系数。δf*与实际前轮转角δf的偏差经过比例、积分、微分3个环节的运算得到转向电机的电压V2,转向电机输出力矩驱动前轮转向模块实现一定的δf,构成PID控制的闭环反馈。

图5 转向电机的PID控制模型
2 线控转向系统结构参数对汽车操纵稳定性的影响
图6~9为一定车速(50 km/h)下车辆转向,且转向电机力矩阶跃输入时,线控转向系统转向模块的主要结构参数对汽车操纵稳定性的影响。
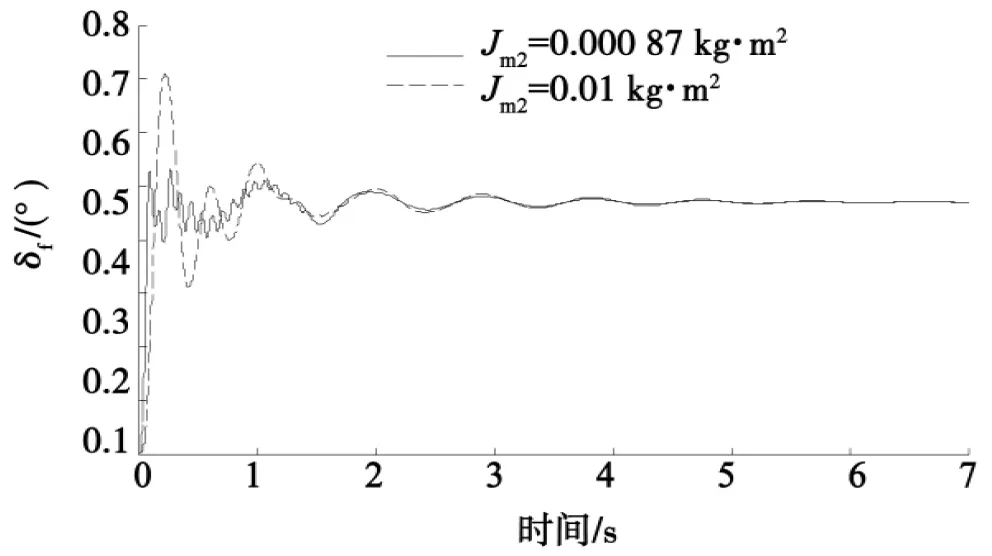
图6 Jm2对δf响应的影响
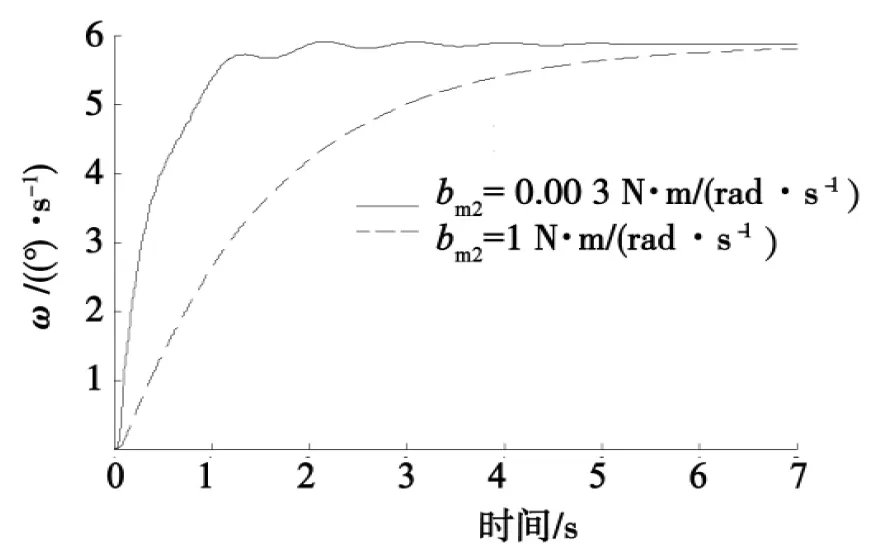
图7 bm2对横摆角速度ω阶跃响应的影响

图8 km2对质心侧偏角β阶跃响应的影响

图9 nm2对车身侧倾角θ阶跃响应的影响
图6分析了Jm2对δf响应的影响。Jm2=0.000 87 kg·m2时,δf峰值时间为0.1 s,超调量为13.31%。Jm2=0.01 kg·m2时,δf峰值时间为0.24 s,超调量为51.24%。可见,转向电机转动惯量过大时,δf响应慢,有较大的超调。图7 对比了不同的bm2对横摆角速度ω阶跃响应的影响。bm2=0.003 N·m/(rad·s-1)时,ω阶跃响应时间为2 s。bm2=1 N·m/(rad·s-1)时,ω阶跃响应时间为7 s。可见,bm2较大时,ω阶跃响应变慢。图8 对比了不同的km2对质心侧偏角β阶跃响应的影响。km2=1 N·m/rad时,β阶跃稳定时间为4 s。km2=132 N·m/rad时,β阶跃稳定时间为2 s。km2过小时,β阶跃响应有较大的振荡。图9 对比了不同nm2对车身侧倾角θ阶跃响应的影响。nm2为10时,θ阶跃响应稳态值为0.13°。nm2为20时,θ阶跃响应稳态值为0.27°。可见,nm2增大时,θ阶跃响应的稳态值增大。以上分析可见,转向电机的Jm2、bm2、km2、nm2等结构参数对汽车操纵稳定性有较大影响,优化设计时可作为优化变量。
3 结论
1)魔术公式轮胎模型可较好的反映整个转向中的轮胎动力学特性。
2)合理设计线控转向系统的结构参数,可提高汽车的操纵稳定性。
[1]Kazemi R,Janbakhsh A.A Nonlinear Adaptive Sliding Mode Control for Vehicle Handling Improvement Via Steer-by-Wire[J].International Journal of Automotive Technology,2010,11(3):345-354.
[2]Zheng B, Anwar S.Yaw Stability Control of a Steer-by-Wire Equipped Vehicle Via Active Front Wheel Steering[J].Mechatronics, 2009, 19( 6):799-804.
[3]田杰,陈宁,高翔.车辆线控转向系统的分数阶鲁棒控制研究[J].动力学与控制学报,2009,7(1):71-74.
[4]胡静波,王同建,罗士军,等.装载机线控转向系统模糊控制算法[J].吉林大学学报:工学版,2008,38(1):21-26.
[5]于蕾艳, 赵万忠,伊剑波.电动汽车线控转向系统性能分析与参数优化[J].计算机仿真,2013,30(3):169-172.
[6]于蕾艳,贠平利,伊剑波,等.线控转向系统的神经网络模型与模糊控制[J].山东交通学院学报, 2013,21(4):1-5.
[7]于蕾艳,贠平利,鲍长勇,等.基于模糊PID控制的线控转向系统侧向稳定性[J].山东交通学院学报,2014,22(1):4-7.
[8]Sharif-U H M, Anwar S.Yaw Stability Control System for an Automobile Via Steer-by-Wire[C]//Proceedings of 4th International Conference on Electrical and Computer Engineering.Bangladesh: IEEE Computer Society,2006:345-348.
[9]Kueperkoch S, Ahmed J, Kojic A, et al.Novel Vehicle Stability Control Using Steer-by-Wire and Independent Four Wheel Torque Distribution[J].American Society of Mechanical Engineers, Dynamic Systems and Control Division, 2003, 72(1):413-420.
[10]Im, Jae-Sung, Ozaki F, Matsushita T.Experimental Study on Steer-by-Wire System with Bilateral Control[C]//Proceedings of the 2007 4th IEEE International Conference on Mechatronics.Japan: IEEE Computer Society,2007:1-6.
[11]于蕾艳.汽车线控技术[M].东营:中国石油大学出版社,2013.
[12]Yu Leiyan.Research on Control Strategy and Bench Test of Automobile Steer-by-Wire System[C].IEEE Vehicle Power and Propulsion Conference (VPPC), 2008,9:266-271.
[13]郑香美,高兴旺,赵志忠.基于“魔术公式”的轮胎动力学仿真分析[J].机械与电子,2012(9):16-20.
[14]朱盈,朱俊.多种PID控制及其仿真比较[J].工业控制计算机,2010,23(1):53-55.
[15]杨巨庆, 黄健,段丽华.PID控制技术与应用[J].哈尔滨师范大学自然科学学报,2004,2(2):76-79.
[16]全定可,白海涛,马惠铖.PID控制与智能控制的融合[J].科技资讯,2008(32):1-20.
AnalysisforEffectofSteering-by-WireSystemonAutomobileHandlingStability
YULei-yan,JINTao,YIJian-bo,BAOChang-yong,ZHENGYa-jun
(SchoolofElectromechanicalEngineering,ChinaUniversityofPetroleum(ShandongCampus),Qingdao266580,China)
The dynamics model of the steering-by-wire system is established based on the MATLAB/Simulink
software. Then structural parameters of its key parts such as the moment inertia, damp coefficient and stiffness of the steering motor which affect the automobile handling stability are analyzed. The automobile handling stability can be improved by designing reasonable structural parameters of the motor of the steering-by-wire system properly.
steering-by-wire system; handling stability; steering motor; parameter; dynamics model
杨秀红)
2013-12-04
国家自然科学基金资助项目((51005248,51005115);中央高校基本科研业务费专项资金资助(11CX04039A); 国家留学基金资助(20133018);青年教师教学改革项目(QN201319)
于蕾艳(1980—),女,山东烟台人,中国石油大学(华东)副教授,主要研究方向为车辆动力学与控制.
10.3969/j.issn.1672-0032.2014.03.002
U463.4
A
1672-0032(2014)03-0006-04

