提高地月转移轨道入轨段初轨精度的技术途径*

茅永兴，沐俊山，宋叶志，钟德安，3

(1.中国卫星海上测控部，江苏 江阴 214431 ；2.上海卫星工程研究所，上海 200240；3.飞行器海上测量与控制联合实验室，江苏 江阴 214431;4.中国科学院 上海天文台，上海 200030)



提高地月转移轨道入轨段初轨精度的技术途径*

茅永兴1,2,3,**，沐俊山1，宋叶志4，钟德安1，3

(1.中国卫星海上测控部，江苏 江阴 214431 ；2.上海卫星工程研究所，上海 200240；3.飞行器海上测量与控制联合实验室，江苏 江阴 214431;4.中国科学院 上海天文台，上海 200030)

针对星箭分离前、后两段数据处于不同的飞行轨道，经典的轨道计算方法无法实现两段外测数据联合参与定轨，入轨段初轨精度难以进一步提高的问题，通过分析星箭分离时刻轨道半长轴确定精度与测量误差、轨道偏心率之间的关系，提出了提高站址坐标测量精度、采用分布式船姿船位测量体制以提高姿态测量精度、采用卫星测高数据计算任务海域垂线偏差并对船姿数据进行修正、船载雷达测速数据的东平台影响修正、合理的数据预处理以及采用基于速度增量修正的定轨新方法等多种技术途径，并重点介绍了基于速度增量修正、可实现星箭分离前后外测数据联合定轨的新方法。仿真计算和任务实测数据验算表明，新方法轨道半长轴确定精度较以往传统方法提高1个数量级以上，有利于后续测控计划制定和测控站的跟踪引导。

地月转移轨道；初轨确定精度；技术途径；速度增量修正；联合定轨

1 引 言

采用运载火箭直接将月球探测器送入地月转移轨道的发射方式后，处于地月转移轨道近地点附近的入轨段测控仍有航天测量船承担，入轨段的初轨确定也是航天测量船承担的重要任务之一。入轨段可用于初轨确定的外测数据有星箭分离前火箭调姿段的80 s跟踪火箭的脉冲雷达和跟踪卫星的USB或UCB外测数据，以及星箭分离后跟踪火箭残骸的脉冲雷达和跟踪卫星的USB或UCB外测数据。受星箭分离时刻分离弹簧作用力的影响，在星箭分离瞬间，火箭残骸和卫星各自获得了一个沿火箭轴向、方向相反的速度增量，因而，星箭分离前的星箭联合体、星箭分离后的火箭残骸、星箭分离后的卫星三者处于3条不同的飞行轨道，即使跟踪同一个目标，由于星箭分离前后两段外测数据分别处于不同的飞行轨道，传统的入轨段初轨确定方法，例如无摄单位矢量法UVM1[1]、有摄单位矢量法PUVM1[1]等，因它们的动力学模型未考虑卫星飞行过程中受外力的影响，因此无法将星箭分离前后的两段数据放在一起定轨，因而初轨确定时参与定轨的数据弧段很短，要么使用星箭分离前的80 s外测数据，要么星箭分离后的数十或一百多秒的外测数据。由于参与定轨的数据弧段短，入轨段初轨确定精度难以进一步提高。

另外，发射不同轨道的航天器(如小偏心率的近地轨道航天器、大偏心率的同步转移轨道航天器、超大偏心率的地月转移轨道航天器等)，运载火箭的入轨段飞行程序和飞行轨道高度基本相同，也就是说，能用于入轨段初轨确定的外测数据的弧段长度也基本相同。尽管承担入轨段测控任务的航天测量船有时会调整，但各船的测量设备相同、精度指标相同、数据处理得到的实际测量精度变化不大且均在指标范围内，然而，从以往历次任务的实际定轨精度情况看，入轨段的初轨确定精度会随着轨道偏心率的增大而下降，特别是半长轴a的精度。对于小偏心率轨道(偏心率为0.1左右)航天器发射任务，传统初轨确定方法的短弧段外测数据(数十秒)的初轨确定精度(半长轴a误差，下同)一般为1 km左右；对于大偏心率轨道(偏心率小于0.79)的航天器发射任务，传统初轨确定方法的短弧段外测数据的初轨确定精度一般为数公里至十多公里[2]；但在地月转移轨道(偏心率大于0.96，入轨段飞行轨道接近于一条抛物线)航天器发射任务中，传统初轨确定方法的短弧段外测数据的初轨确定精度为数百乃至千公里量级，半长轴a误差比一般的大偏心率轨道大1～2个数量级。

为什么参与定轨的外测数据弧段及其长度相同、测量数据的测量精度相同，对于不同偏心率轨道航天器发射任务，其入轨段的初轨确定精度差异如此之大？通过哪些技术途径可以进一步提高入轨段的初轨确定精度？本文通过理论分析，给出等精度测量条件下轨道半长轴的确定精度与轨道偏心率的关系，提出了提高超大偏心率轨道入轨段初轨确定精度的具体技术途径，并重点探讨了基于星箭分离速度增量修正的星箭分离前后数据的联合定轨方法。

2 测量误差、轨道半长轴确定误差与轨道偏心率间的关系

只要承担入轨段测控任务的航天测量船的各测量设备工作正常，其测量精度可保证在设备的精度指标范围内，不同的发射任务，其测量精度基本上是一致的，它与航天器的轨道偏心率无关;并且用于入轨段初轨确定的主用测量数据——星箭分离前火箭调姿段的脉冲雷达、USB或UCB外测数据，其弧段长度也是基本相同的，为什么半长轴a的误差会随着偏心率的增加而急剧上升？我们不妨从理论上加以分析。

在我国CZ-3A系列运载火箭的发射弹道和航天器飞行轨道设计时，大多数航天器的近地点(入轨段附近)高度hp为200 km左右，我们不妨假设hp=200 km，则根据近地点地心距rp与半长轴a和偏心率e的关系式[2]

(1)

对于轨道偏心率e分别为0.50、0.75、0.96时，轨道半长轴a则分别为13 156.280 km、26 312.560 km、164 453.500 km，轨道半长轴a随偏心率的变化趋势与实际任务中的半长轴a的定轨精度变化趋势基本一致。

我们再从经典的活力公式分析相同的测量误差对不同偏心率轨道的半长轴确定精度的影响。

这里，假定星箭分离时刻(一般在近地点附近)的地心距r为6 578.140 km，对应轨道偏心率e分别为0.50、0.75、0.96时的轨道半长轴a分别为13 156.280 km、26 312.560 km、164 453.500 km，则根据经典的活力公式[2]

(2)

可以得到它们的速度分别为9 533.733 m/s、10 297.608 m/s、10 897.964 m/s。

现在假定不同偏心率轨道航天器发射任务中航天测量船的外测精度是相当的，并且假定船载站的船姿船位误差(含高程误差)、船摇引起的天线位置变化、星地设备的距离零值误差、USB设备自身的测量误差等多种误差源合成后，折算成地心距误差Δr为30 m，假定船载USB站的船速误差、船摇引起的测速误差、船体升沉引起的测速误差(目前尚未考虑)[3]、USB设备自身的测速误差等多种误差源[4]合成后折算成卫星的运动速度误差Δv为1.0 m/s，则根据变换后的活力公式

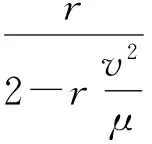
(3)

可以得到它们各自对于不同偏心率轨道的半长轴a的影响是不一样的，结果见表1。

表1 测量误差对不同偏心率轨道半长轴a的影响Table 1 Effect of measurement error on semi-major axis of different eccentricity orbit

从表1结果可以看出，虽然在不同偏心率轨道航天器的发射任务中，航天测量船的外测精度基本一致，即具有相同的测量误差，但对轨道半长轴a的确定精度的影响差异很大，偏心率越接近于1，测量误差对半长轴a的影响越敏感，这与实际任务中半长轴a的定轨精度变化趋势基本一致。

3 提高地月转移轨道入轨段初轨确定精度的技术途径

3.1提高外测数据的整体测量精度

测量误差是影响定轨精度的最主要因素。从以往多次航天发射任务的入轨段初轨确定结果看，箭载卫导定位数据的初轨确定精度都比较高，使用星箭分离前的15 s无动力保姿态飞行段数据单点定轨，近地近圆轨道半长轴误差起伏很小，通常为1 km左右，多点综合定轨半长轴误差通常为百米量级；同步转移轨道单点定轨的半长轴误差起伏也比较小，通常为2 km左右，多点综合定轨半长轴误差为1 km左右；地月转移轨道单点定轨的半长轴误差起伏比较大，在某次任务中达到200 km左右，多点综合定轨半长轴误差小于50 km。目前装箭的卫导接收机其定位精度其实也不是很高，如果船载外测数据的综合测量精度能达到目前装箭的卫导定位精度，则可以大大提高入轨段外测数据的初轨确定精度。由于航天测量船外测数据的误差源比较多，影响航天测量船外测数据的综合测量精度的因素较多[4]，提高航天测量船综合测量精度有以下技术途径。

(1)提高站址坐标测量精度

船载雷达测量数据是基于瞬时站址的惯导地平坐标系下的，站址坐标是惯导地平坐标系的原点，其测量精度的高低直接影响测轨数据的整体精度，从而影响定轨精度。

以往船载卫导系统工作不是很稳定，只是使用卫导工作正常期间的定位结果对惯导位置(经纬度)进行校准，任务中测量船中心机使用惯导输出的经纬度作为瞬时站址惯导地平坐标系原点的经纬度，使用任务前卫导工作正常时的高程统计值作为瞬时站址导地平坐标系原点的高程。因此，水平位置误差较大，入轨段短弧段测控任务中达百米量级，高程误差也达米量级甚至十米量级。

随着船载卫导系统的设备换型，系统工作的稳定性、可靠性得到了一定程度的提高，实时任务中，测量船中心机可以使用卫导实时定位结果的经纬度作为瞬时站址惯导地平坐标系原点的经纬度，受船载卫导系统自身精度的限制，坐标系原点的高程值仍沿用以往的方法。因此，站址坐标的水平精度较以往得到了一定程度的提高，使得水平精度与高程精度处于同一数量级(十米量级)，但仍有较大的提升空间，通过设备换型、采用一些新的技术，使测量船的站址坐标定位精度达到1 m以内是完全可能的。

(2)采用分布式船姿船位测量体制[5]

目前采用的是集中式船姿船位测量体制，除前面提到的站址坐标误差影响惯导地平坐标系的原点精度外，船摇测量误差、变形测量误差将直接影响惯导地平坐标系下测量数据的测角精度。在设备测量精度无法进一步提高的情况下，减少测量环节，减少误差源也是提高整体测量精度的有效方法。因此，采用分布式船姿船位测量体制是今后的发展趋势，从而可以减少船体变形测量环节，减少一项误差源。同时，在该测量体制下，可采用星惯组合测量系统，可使船摇测量精度得到一定程度的提高。

(3)基于卫星测高数据精确计算任务海域垂线偏差

测量船基准坐标系——惯导地平坐标系的基准平面是与当地铅垂线垂直的大地水平面，而其站址坐标是由卫导给出的WGS-84坐标系下的大地经纬度，惯导地平坐标系下的测量数据转换到其他坐标系时，坐标系旋转必须使用天文经纬度，因此，需要对大地经纬度进行垂线偏差修正。由于以前无法确定任务海域的垂线偏差，所以忽略了两者之间的差异，也就是说，垂线偏差引起的误差直接带入到测量数据的处理过程中，其定轨精度受到了一定的影响。随着技术的发展，目前可以通过卫星测高数据计算任意海域的重力异常、垂线偏差等相关地球物理参数，使航天测量船外测数据在坐标系转换时考虑垂线偏差修正成为可能。

(4)对船载雷达测速数据进行船摇、航速、升沉引起的误差修正

由于航天测量船没有配备船体升沉测量设备，船用惯导也未安装天向(垂直方向)加速度计，因此无法直接获取航天测量船惯导平台中心垂直方向的运动速度，因而也无法对雷达测速数据进行由此引起的测量误差的修正。同时，目前航天测量船配备的设备(如计程仪、惯导、卫导)提供使用的航速数据精度也不是很高，所以，测量船中心机在数据预处理时，只是进行了理论设计航速和实际船摇对测速数据影响的简化修正。目前，市场上的商用卫导定位精度较以前有较大提高，可以得到卫导天线位置精度较高的速度矢量，通过坐标系转换，也可以得到惯导平台中心的速度矢量，从而为船载雷达测速数据进行水平运动速度修正和垂直运动速度修正，进一步提高船载雷达测速数据的精度成为可能。

3.2改进定轨方法以延长同时参与定轨的数据弧段

星箭分离瞬间，受弹簧分离力的影响，卫星和火箭分别获得一个速度增量，使得它们的飞行轨道发生了改变，从而传统的初轨确定方法无法将这两段测轨数据放在一起定轨，因而参与定轨的数据弧段较短(星箭分离前80 s或星箭分离后数十秒至一百多秒)，定轨精度无法进一步提高。

通过建立星箭分离时刻速度增量修正模型，即可得到星箭分离时刻星箭分离动作完成前、后两组状态矢量，从而可以实现星箭分离前、后两段外测数据的联合定轨，延长了定轨数据弧段。

(4)

则对于星箭分离前外测数据的条件方程组为

(5)

对于星箭分离后外测数据的条件方程组为

(6)

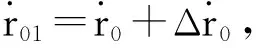
(7)

公式(5)、(7)经整理后为

(8)

(9)

公式(8)对应星箭分离前的测轨数据，公式(9)对应星箭分离后的测轨数据，两类条件方程求解变量一致，可以放在一起求解，从而实现星箭分离前后的两段测轨数据的联合定轨，延长了参与定轨的测轨数据弧段，可有效提高初轨确定精度。

3.3完善数据预处理方法

船载站的特点决定了其综合测量精度的高低。在惯导地平坐标系下，测量误差分布在各测量元素中，包括测距误差Δρ、方位角误差ΔA、俯仰角误差Δh以及站址坐标(大地经度和高程)误差ΔL、ΔB、ΔH。任务中，尽管在数据预处理时已经分别进行合理性检验、野值剔除与补点、平滑等处理，但各类测量元素其曲线特性有较大差异，有的测量元素在某些时段的曲线曲率较大，不适合大区间平滑，目前的平滑区间仅为2 s，因此，某些周期大于2 s且不固定的大区间振荡引起的误差将无法得到抑制，仍直接带入到测量数据中。为此，在定轨前可以再次进行测量数据的预处理，以尽可能提高用于定轨的测量数据精度。例如：将惯导地平坐标系下的测量数据转换至地心坐标系(如J2000地心天球坐标系)，这样，各测量元素的误差将分别投影到地心坐标系的位置矢量ri上，它们各自的误差(特别是系统误差)投影后将会得到相互抑制和抵消。同时，在地心坐标系下，由于卫星入轨段飞行弧段较短，其位置矢量曲线的曲率很小，远小于惯导地平坐标系下方位角和俯仰角数据曲线的曲率，因而可以采用大区间平滑拟合，可有效抑制接近于船摇周期的不明振荡误差，同时通过大区间的微分拟合，可以得到精度较高的速度矢量，从而可有效提高定轨精度。

4 基于速度增量修正的初轨确定新方法

4.1各采样时刻卫星状态矢量求解方法

首先，将惯导地平坐标系下的雷达方位角Ai、俯仰角hi、测距ρi数据转换至J2000地心天球坐标系(惯性坐标系)下，得到各采样时刻的卫星位置矢量ri。

(10)

(11)

其中：

τi=ti-t0

ti为数据采样时刻，t0为参与平滑的数据弧段中点时刻，平滑区间应大于测量数据中包含的非固定周期性振荡的最大周期的3倍。

4.2速度增量修正方法

(12)

其中，A为发射惯性坐标系至J2000地心天球坐标系的转换矩阵，Φ、Ψ为星箭分离时刻发射惯性坐标系下的火箭俯仰姿态角和偏航姿态角，ΔV为卫星在火箭轴向获得的绝对速度增量。则

(13)

4.3动力学条件方程组建立

建立以下有摄初轨计算的基本条件方程组

(14)

则对于星箭分离前的测轨数据，对应的条件方程组为

(15)

对于星箭分离后的测轨数据，对应的条件方程组为

(16)

将式(13)代入，则

(17)

式(15)、(17)求解相同的变量，可以放在一起求解，从而实现星箭分离前后处于两条飞行轨道的两段测轨数据的联合定轨。求解方法可采用最小二乘方法。

5 算例

5.1仿真计算结果

仿真数据为星箭分离前80 s、星箭分离后100 s数据，仿真用标准轨道根数见表2，其中第1组为星箭分离时刻星箭对应分离动作完成前的轨道根数，第2组为星箭分离时刻对应星箭分离动作完成后的轨道根数。表3为叠加的测量数据系统误差和随机误差，表4～6分别给出了用常用的无摄初轨计算的单位矢量法UVM1、有摄初轨计算的单位矢量法PUVM1以及本文方法各500组仿真计算的统计结果。

表2 标准轨道根数Table 2 Standard orbital elements

表3 测量数据系统误差和随机误差Table 3 Systematic error and random error of measurement data

表4 UVM1方法仿真结果Table 4 Simulation results using UVM1 method

表5 PUVM1方法仿真结果Table 5 Simulation results using PUVM1 method

表6 本文方法仿真结果Table 6 Simulation results using method of this paper

仿真计算结果表明，采用本文提出的新方法后，地月转移轨道入轨段初轨确定精度比传统定轨方法提高约2个数量级，定轨精度明显提高。

5.2任务实战数据验算结果

我们使用某航天发射任务船载雷达获取的实测数据进行验算，各种定轨方法的定轨结果偏差(与任务中心事后提供的长弧段精轨比)见表7～9。

任务实测数据验算结果表明，采用本文提出的新方法后，地月转移轨道入轨段初轨确定精度比传统定轨方法提高1个数量级以上，定轨精度得到显著提高。

表7 UVM1方法实测数据计算结果Table 7 Calculation results of real data using UVM1 method

表8 PUVM1方法实测数据计算结果Table 8 Calculation results of real data using PUVM1 method

表9 本文方法实测数据计算结果Table 9 Calculation results of real data using method of this paper

6 结束语

以往入轨段初轨确定方法只考虑使用处于同一条飞行轨道的星箭分离前的火箭调姿段或星箭分离后的测轨数据，因此无法将弹簧分离方式下在星箭分离时刻瞬间产生速度增量而导致星箭分离前后测轨数据处于两条飞行轨道的测轨数据放在一起进行联合定轨，因而参与定轨的数据弧段短，定轨精度难以进一步提高。

本文提出了新的定轨方法，实现了星箭分离前后测轨数据的联合定轨，延长了参与定轨的测轨数据弧段，从而有效提高了初轨确定精度。但是，提高定轨精度还有许多方面的工作要做，正如本文提出的提高测量精度、采用分布式船姿船位测量体制、任务海域垂线偏差获取以及对测量数据的修正等，都需要我们进一步深入研究。当然，解决该问题还有其他技术途径，希望广大读者也参与到我们的研究工作中，提出更多更好的解决方法，共同为我国的航天测控事业做出一份贡献。

[1] 茅永兴.航天器轨道确定的单位矢量法[M].北京：国防工业出版社，2008:155-183. MAO Yong-xing. The Orbit Determination Method for Spacecraft based on Unit Vector Method [M].Beijing：National Defense Industry Press,2008:155-183. (in Chinese)

[2] 茅永兴，倪小秋，张忠华,等.航天发射任务星箭分离前调姿段测轨数据定初轨精度分析[J].飞行器测控学报，2010,29(2):44-49. MAO Yong-xing, NI Xiao-qiu, ZHANG Zhong-hua，et al.Analysis of Orbit Determination Precision with Data in Attitude Adjusting Segment before Separation of Satellite-rockets in Space Launch Mission[J].Journal of Spacecraft TT&C Technology, 2010，29(2)：44-49. (in Chinese)

[3] 李晓勇，张忠华，船载外测设备测速数据的误差修正[J].电讯技术，2006，46(5)：131-135. LI Xiao-yong,ZHANG Zhong-hua.Error Correction of Velocity Measuring Data of Ship-borne Exterior Trajectory Measurement Equipment[J]. Telecommunication Engineering,2006,46(5):131-135. (in Chinese)

[4] 朱伟康，李辉芬，陈德明,等，提高航天测量船定轨精度的途径[J].电讯技术，2012，52(5)：658-662. ZHU Wei-kang,LI Hui-fen,CHEN De-ming,et al.Ways to Improve Orbit Determination Precision of Space TT&C Ships[J].Telecommunication Engineering, 2012, 52(5):658-662. (in Chinese)

[5] 茅永兴，张同双，朱伟康,等，基于星惯组合的分布式船姿船位测量体制研究[J].飞行器测控学报，2013，32(1)：23-26. MAO Yong-xing,ZHANG Tong-shuang,ZHU Wei-kang,et al. Research on Measurement System for Distributed Ship-Pose and Ship-Location Based on SS/INS Integrated Navigation Systems[J].Journal of Spacecraft TT&C Technology, 2013，32(1)：23-26. (in Chinese)

[6] 陆本魁，李剑峰，马静远，等.一种有摄初轨计算的单位矢量法[J].宇航学报，1999，20(1)：14-20. LU Ben-kui,LI Jian-feng,MA Jing-yuan,et al. A Method of Perturbed Initial Orbit Determination[J].Journal of Astronautics,1999，20(1)：14-20.(in Chinese)

MAO Yong-xing was born in Haimen,Jiangsu Province,in 1966.He is now a senior engineer of professor with the M.S. degree.His research concerns spacecraft orbit determination and TT&C.He has published more than 30 papers.

Email:MYX8282@tom.com

TechnicalApproachesforImprovingAccuracyofInitialOrbitDeterminationinInjectionPhaseofEarth-MoonTransferTrajectory

MAO Yong-xing1，2,3，MU Jun-shan1，SONG Ye-zhi4，ZHONG De-an1，3

(1.China Satellite Maritime Tracking and Control Department，Jiangyin 214431,China；2.Shanghai Institute of Satellite Engineering, Shanghai 200240,China;3.Joint Laboratory of Ocean-based Flight Vehicle Measurement and Control，Jiangyin 214431，China;4.Shanghai Astronomical Observatory,Chinese Academy of Sciences，Shanghai 200030，China)

In the injection phase where two segments of measurements are obtained for different trajectories, the classical orbit determination method can not implement a united estimation. It is difficult to further improve the accuracy of the initial orbit determination. The paper improves the position measurement accuracy of tracking stations by analyzing the relation among semi-major axis, tracking errors and orbit eccentricity. A distributed ship position-attitude measurement architecture is adopted to improve the accuracy of ship attitude. The altitude measurements by satellites are used to estimate gravimetric plumb line deflection of the mission area and improve the ship attitude, velocity tracking data obtained by ship-borne radar. Other new methods, such as optimal data preprocessing and injection velocity correction, are also proposed. Numerical results show that the new approaches improve the accuracy over one order of magnitude than the traditional method and will benefit to the tracking plan and guidance of downrange tracking stations.

earth-moon transfer trajectory; initial orbit determination accuracy; technical approaches; injection velocity correction; united orbit determination

10.3969/j.issn.1001-893x.2014.06.005

茅永兴，沐俊山，宋叶志，等.提高地月转移轨道入轨段初轨精度的技术途径[J].电讯技术，2014,54(6):719-725.[MAO Yong-xing，MU Jun-shan，SONG Ye-zhi,et al.Technical Approaches for Improving Accuracy of Initial Orbit Determination in Injection Phase of Earth-Moon Transfer Trajectory[J].Telecommunication Engineering,2014,54(6):719-725.]

2014-01-26；

：2014-05-04 Received date:2014-01-26；Revised date：2014-05-04

：MYX8282@tom.comCorrespondingauthor：MYX8282@tom.com

V412.4

：A

：1001-893X(2014)06-0719-07

茅永兴(1966—)，男，江苏海门人，硕士，研究员，主要从事航天器轨道确定方法及航天测控技术研究，已出版专著《航天器轨道确定的单位矢量法》，发表论文30余篇，获国家级及军队级科技进步奖16项。

**