多信道认知用户能量高效的最优功率分配*

姜 志,史治平

(1.中国工程物理研究院，四川 绵阳 621900；2.电子科技大学 通信抗干扰技术国家级重点实验室，成都 611731)



多信道认知用户能量高效的最优功率分配*

姜 志1，**,史治平2

(1.中国工程物理研究院，四川 绵阳 621900；2.电子科技大学 通信抗干扰技术国家级重点实验室，成都 611731)

针对多信道认知用户能量效率问题，提出认知用户能量效率优化模型，进而优化传输功率和感知帧长。首先，多信道认知用户基于多带宽联合能量检测方案，在一定传输功率和干扰功率限制下，建立了以单位数据能耗为目标的最优化问题；其次，通过非线性分式规划的对偶优化将目标函数转换为内点法求解形式；然后，结合内点法和二分法给出算法流程，进而配置最优功率和感知时间。仿真结果表明，对应不同通信环境采用该优化方法都能通过配置最优功率和感知时间达到能量效率最优。

认知无线电；能量效率；功率分配；非线性分式规划

1 引 言

随着无线通信普及，通信链接数目不断增加而带来频谱资源稀缺，并且现有频谱分配制度导致频谱资源利用率十分低，认知无线电[1]是针对该问题提出的一种新技术。初期对于认知无线电的研究主要集中在感知技术、资源分配，如文献[2]从单用户基于多信道并行传输模型以系统吞吐量为目标，分析了传输功率和帧结构对系统吞吐量对能效的影响。而随着通信普及程度提高，对认知无线电的能效研究是一个较新的方向，研究在逐步增多：文献[3]针对单用户认知模型，分析了传输时间与能量效率的关系；文献[4]基于认知用户序列感知问题，分析了感知顺序、接入策略、功率分配对能量效率的影响；文献[5]针对单用户认知模型，分析了感知时间和传输时间与能量效率的关系。对于能量效率的分析都是基于不同系统模型，建立能量效率模型给出对应的优化方案。

目前，已有文献主要分析单用户单信道传输的能量效率，模型与文献[2]一致，优化目标与文献[3-5]一致，均为能量效率。本文从认知用户同时M个子信道传输数据[2]，分别考虑Underlay和Overlay接入模型下，从能量消耗角度出发，以能量效率为目标，分析两种接入模式下数据传输量与对应的能量消耗，建立能量效率优化数学模型，讨论关于传输功率的最优化问题；验证目标函数是一个非线性分式规划问题，推导出功率分配的数学表达式，并给出相应算法流程；最后仿真验证了算法的合理性，结合实际参数分析了不同传输功率、授权用户空闲先验概率、子信道数目将得到不同的最优功率分配和感知时间而达到不同能量效率。

2 认知用户系统模型

无论认知用户采用Underlay还是Overlay模型[6]，宽带频谱等分为M个不交叠的窄带频谱，认知用户与授权用户子信道上并行传输数据，包含一个授权用户链路和一个认知用户链路，如图1所示。授权用户和认知用户都在M个信道上传输，第i信道PU-Tx 与SU-Rx 之间瞬时信道功率增益为gps,i，SU-Tx 与PU-Rx 之间的瞬时信道功率增益为gsp,i，SU-Tx 与SU-Rx 之间瞬时功率增益为gss,i。假设每个信道都是平稳衰落信道且信道功率增益服从各态历经和平稳分布，子信道之间相互干扰很小，可以忽略。

认知用户采用文献[7]给出的多带宽联合能量检测方案，可提高频谱利用率和减少对授权用户的干扰，分别检测M个信道上的授权用户接入状态。认知用户接收端信号首先经过M个降频器，然后通过M个能量检测器，如图2所示。

图2 认知用户带宽检测装置框图Fig.2 Block diagram of cognitive user′s wideband detector

每个信道的感知问题都是一个独立的二元假设检验，频段k若处于空闲状态表示为H0,k，若处于占用状态表示为H1,k。假设授权用户信号为复PSK信号，认知用户噪声服从独立同分布的循环对称复高斯分布，均值和方差分别为0、σ2。

基于上述模型，认知用户第i信道的虚警概率为[8]

(1)

其中，Q()为Q函数，Q-1()为Q函数反函数，τ表示感知时间，γi为接收到授权用户的信噪比，fs为采样频率 ，φde,i为认知用户的目标检测概率。

认知用户每个子信道的帧结构都是相同的，该结构是通用的认知网络模型，如图3所示。帧长是固定的，确定最优感知帧长，即是达到能量效率为最优时对应的感知时间长度。

图3 认知用户的帧结构Fig.3 Frame structure for cognitive user

C1：认知用户成功检测授权用户的空闲状态，概率分布α0,i为

C2：认知用户误检授权用户的占用状态，概率分布α1,i为

C3：认知用户误检授权用户的空闲状态，概率分布β0,i为

C4：认知用户成功检测到授权用户的占用状态，概率分布β1,i为

3 Underlay和Overlay能效优化模型

3.1Underlay能效模型

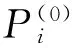
由第2节中认知用户的感知结果可能性，可以得到每种情况认知用户对应的传输速率：

(2)

(3)

(4)

(5)

因此，第i信道认知用户的平均速率表示为

Ci=α0,ir00,i+α1,ir01,i+β0,ir10,i+β1,ir11,i

(6)

同理，第i信道认知用户的传输总功率为

(7)

考虑认知用户的长期功率预算，则平均功率限制表示为[9]

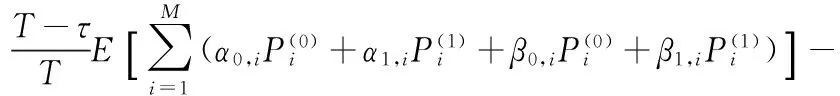
(8)

其中，Pav表示认知用户最大平均传输总功率，E[]表示数学期望。

同样，保证对授权用户的通信质量，需要限制认知用户在C3、C4情形下传输时的功率，子信道的平均干扰功率限制为[10]

(9)其中,Ψ表示授权用户能够接受的最大平均干扰功率。

综上，Overlay接入模型时，认知用户的能效优化问题为

(10)

其中

(11)

(12)

优化目的就是得到认知用户传输功率和帧结构，使能耗η(τ,P(0),P(1))最小而能量效率最优。

3.2Overlay能效模型

与Underlay接入模型不同的是Overlay接入模型时认知用户，只在授权用户闲置信道时传输数据。设认知用户的第i信道传输功率为Pt,i。

Overlay接入模式时，认知用户只有C1和C3两种情形有数据传输，其对应的传输速率为

C1：r0,i=Blb(1+giPt,i)

(13)

(14)

除速率外，其他符号与第3.1节一致。

因此，第i信道认知用户的平均速率为

Ci=φ(H0,i)(1-φfa,i(τ))r0,i+φ(H1,i)(1-φde,i)r1,i

(15)

第i信道认知用户的传输功率为

Pi=φ(H0,i)(1-φfa,i(τ))Pt,i+φ(H1,i)(1-φde,i)Pt,i

(18)

与3.1节一样，认知用户的平均功率与限制功率限制分别为[9]

(17)

(18)

Overlay接入模型时认知用户的能效优化目的也是配置传输功率和帧结构，使单位能耗最小而能量效率最优，其能量效率模型为

(19)

其中

(20)

(21)

4 优化算法

由能量效率优化目标函数式(10)和式(19)可以看出，接入功率分配和虚警概率是相互独立的，即目标函数关于自变量功率与感知时间是相互独立的。因此，对于感知时间τ可以在取值范围内利用一维穷举法求出最优值；而固定感知时间时，最优功率分配采用非线性分式规划。

4.1Underlay模型

优化功率分配时，将感知时间当作一个常数处理。式(10)中E(τ,P(0),P(1))是凸函数和可微的，C(τ,P(0),P(1))是凹函数和可微的，限制条件也是凸函数和可微的。因此，优化问题满足非线性分式规划[10]的对偶优化，其对偶问题可以表示为

s.t.Pt,i≥0,i=1,2,…,M

式(8),式(9)

(22)

设F(λ)=min{E(τ,P(0),P(1))-λC(τ,P(0),P(1))}，限制条件与式(22)相同，则对偶问题之间存在如下关系：

结论1：

若

当且仅当

F(λ*)=F(λ*,P(0)*,P(1)*)= min{E(τ,P(0),P(1))-λ*C(τ,P(0),P(1))=0。

证明：充分性：

λ*=E(τ,P(0)*,P(1)*)/C(τ,P(0)*,P(1)*)≤E(τ,P(0),P(1))/C(τ,P(0),P(1))

(23)

可得

E(τ,P(0),P(1))-λ*C(τ,P(0),P(1))≥0

(24)

E(τ,P(0)*,P(1)*)-λ*C(τ,P(0)*,P(1)*)=0

(25)

因此

F(λ*)=F(λ*,P(0)*,P(1)*)= min{E(τ,P(0),P(1))-λ*C(τ,P(0),P(1))}=0

(26)

必要性：

F(λ*)=F(λ*,P(0)*,P(1)*)=E(τ,P(0)*,P(1)*)-λ*C(τ,P(0)*,P(1)*)=0

(27)

可得

E(τ,P(0),P(1))-λ*C(τ,P(0),P(1))≥F(λ*)=0

(28)

E(τ,P(0)*,P(1)*)-λ*C(τ,P(0)*,P(1)*)=0

(29)

λ*≤E(τ,P(0),P(1))/C(τ,P(0),P(1))

λ*=E(τ,P(0)*,P(1)*)/C(τ,P(0)*,P(1)*)

(30)

因此，可证

λ*=E(τ,P(0)*,P(1)*)/C(τ,P(0)*,P(1)*)= min{E(τ,P(0),P(1))/C(τ,P(0),P(1))}

(31)

结论2：F(λ)是关于λ的单调递减函数。

证明：

设λ1<λ2，且P(0)*(λ1)、P(1)*(λ1)及P(0)*(λ2)、P(1)*(λ2)对应的最优功率分配，则

F(λ1)=min{E(τ,P(0),P(1))-λ1C(τ,P(0),P(1))}=E(τ,P(0)(λ1),P(1)(λ1))-λ1C(τ,P(0)(λ1),P(1)(λ1))>E(τ,P(0)(λ1),P(1)(λ1))-λ2C(τ,P(0)(λ1),P(1)(λ1))> min{E(τ,P(0),P(1))-λ2C(τ,P(0),P(1))}=F(λ2)

(32)

由结论1,、结论2可知，在已知λ*时，可由L(τ,P(0),P(1))分别对P(0)、P(1)微分并求驻点，则可得最优功率分配为([x]+表示max(0,x))

(33)

(34)

其中

(35)

(35)

由结论1知F(λ)=0时，对应的优化问题最优值与参数λ*是一一对应的；而且由结论2可知，F(λ)是单调递减函数，对F(λ)=0对应λ值可采用二分法求解，即可求得最优λ*。因此，只要求得λ*，代入式(33)、(34)即得最优功率分配。

采用二分法求解重点在于如何求得F(λ)的值，同样，E(τ,P(0),P(1))是凸函数和可微的，-λC(τ,P(0),P(1))是凸函数和可微的，F(λ)满足内点法求解条件，其中内点法是最优化算法的一个标准算法，记为算法1。

算法1:给定感知时间τ′,计算最优λ*。

(1)给定λ∈[λmin,λmax];

(2)重复

1)λ=(λmin+λmax)/2;

2)内点法求解式(22)并计算F(λ);

3)若F(λ)≤0,则λmax=λ;反之，则λmin=λ;

(3)直到λmin-λmax≤ε。

由算法1，可以求得感知时间取值范围内的能量效率曲线，则最优感知时间为

则系统最优功率分配由式(33)、(34)可得。

4.2Overlay模型

参照Underlay模型，Overlay目标函数同样适用于非线性规划对偶优化。

同理，式(19)的对偶优化问题为

(38)

与式(33)、(34)采用相同方法，已知λ*，最优功率分配同样可以对L′(τ,Pt)对Pt微分并求驻点，最优功率分配为

(39)

其中

(40)

(41)

与Underlay模型一样，Overlay模型对应对偶函数式(38)同样满足结论1、结论2对应性质，同样可以结合内点法、二分法给出优化方法，记为算法2。

算法2:给定感知时间τ′,计算最优λ*。

(1)给定λ∈[λmin,λmax];

(2)重复

1)λ=(λmin+λmax)/2;

2)内点法求解(38)并计算F′(λ);

3)若F(λ)≤0,则λmax=λ;反之，则λmin=λ;

(3)直到λmin-λmax≤ε。

由算法2，可以求得感知时间取值范围内的能量效率曲线，则最优感知时间为

(42)

则系统最优功率分配由式(38)可得。

5 数值仿真

对于Underlay、Overlay两种接入模式，根据第4节提出的能量效率优化算法以及实际通信参数可以分析对系统能效提升情况。仿真参数参照文献[2,4]，实际通信参数不会影响算法的可行性。带宽为6 MHz，N0/2为-204 dBW，Nf为10 dB，载波频率f1=700 MHz，fi+1-fi=B,i=1,2，…,M-1，链路余量为10 dB，BER为10-5，感知功率为200 mW，授权用户功率为10 mW，认知用户帧长为100 ms，授权用户空闲概率φ(H0,i)分别为0.8、0.6、0.4，平均功率限制为500 mW，干扰功率限制为-5 dB、-10 dB、-15 dB、-20 dB，目标检测概率为0.9。

5.1不同干扰限制与能耗

图4与图5表示感知时间变化、Underlay和Overlay下，信道数目为3、平均功率限制固定为1 W、φ(H0,i)=0.6时，不同干扰功率限制相对应的单位数据能耗。从两图都可以看出，在干扰功率限制与平均功率限制下，最优能量效率都是中间能量效率高，两端能量效率低。当感知时间较小时，感知时间短而虚警概率低，错失了传输机会，则传输速率减少和能量效率降低；而当感知时长增加到一定时，虚警概率减少及传输速率增加不能补偿频谱感知带来的能量消耗，则能量效率降低。图中的极小值点为优化目标最优感知时间，对应的能耗为最优。从图4和图5可以看出，随着干扰功率限制逐渐严格，单位数据消耗的能量增加而能量效率降低。传输功率降低而信噪比降低，从而传输速率、能耗增高、效率降低。

图4 Underlay不同干扰限制与能耗关系Fig.4 The relationship between different interference restrictions and energy consumption for Underlay

图5 Overlay不同干扰限制与能耗关系Fig.5 The relationship between difference interference restrictions and energy consumption for Overlay

5.2干扰功率和先验概率与最优能耗

信道数目为3，平均功率限制为1 W时，图6显示不同授权用户状态分布、不同干扰功率限制对最优能耗的影响。在干扰功率限制、平均功率限制以及φ(H0,i)都相等的情况下，可以明显看出Underlay比Overlay能够获得更优的能量效率，由于Underlay在相同的限制下能够获得更多传输机会，得到更大的系统吞吐量，而单位消耗更低。当授权用户先验概率的相同时，随着干扰功率限制不断严格，Underlay与Overlay两者的能量效率之间的差距是逐渐缩小的，当干扰功率限制达到某个值时，两者几乎一致。因为限制越小，则Underlay与Overlay的功率分配方案十分接近。对于相同的干扰功率限制，先验概率越小，两种接入模式的最优能量效率是越来越差的。φ(H0,i)减小，意味着授权用户占用信道概率增加，而认知用户接入信道几率变小，传输速率降低，能耗增加而能效降低。

图6 不同干扰功率和空闲先验概率下的最优能耗Fig.6 Optimal energy consumption under different restrictions of interference power and priori probability of idle state

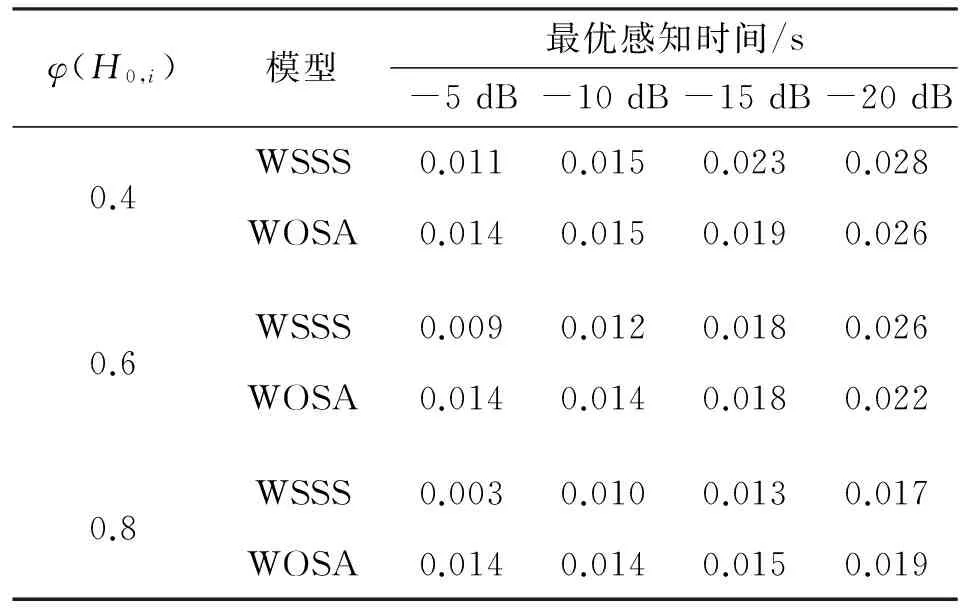
表1 不同干扰功率和空闲先验概率下的最优感知时间Table 1 Optimal sensing time under different interference power and priori probability of idle state

从表1可以看出，两种模型的最优感知时间伴随干扰功率限制逐渐严格而增加，为了授权用户通信质量，认知用户需要更准确的感知结果，感知部分能耗增加，而随着授权用户接入信道概率增加，最优感知时间也是相应变大的。

表2 不同干扰功率和空闲先验概率下的吞吐量Table 2 Throughput under different interference power and priori probability of idle state

从表2可以看出，系统达到最优能效时的吞吐量都满足基本需求；还可以看出，宽带感知频谱共享比宽带机会接入同样限制情况下能够达到更大的吞吐率，能量效率更优。

5.3信道数目和先验概率与最优能耗

图7为干扰功率限制为-10 dB、平均功率限制为1 W时，信道数目和授权用户接入情况，即空闲概率与两种接入模型能耗的关系。传输信道数目增加，单位能耗是增加的，降低了系统能量效率。信道数目增加时，前几个信道载波频率相同时，相异信道的载波频率变大，进而路径损耗变大，因此对应子信道传输速率降低而降低能效。同样，图7显示当授权用户接入信道概率降低时，Underlay与Overlay之间最优能耗是逼近的，与图6结果相一致。

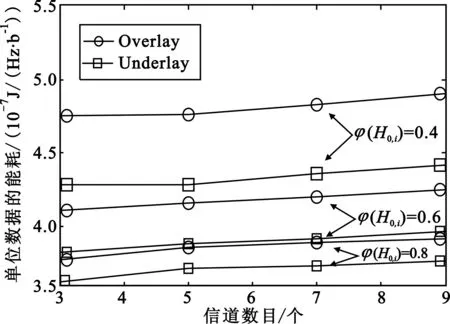
图7 不同信道数目和空闲先验概率下的最优能耗Fig.7 Optimal energy consumption under different number of channels and priori probability of idle state

6 结 论

相同的条件下，优化配置传输功率和感知时间可以使认知用户能量效率达到最优。对于不同的条件，即使最优配置能量效率也是不尽相同的。实际系统采用本文提供的方法，最优能量效率分析都是基于具体模型，解决能量效率在不同条件下的优化问题，同时，其也是一个自适应过程，需要根据通信环境不断调整通信参数。而本文是基于固定感知帧长，优化了感知时间和传输功率。对于传输时间也作为变量的情形还未考虑，这类型情况对感知时间和传输时间的优化不能简单采用穷举法，对两者联合优化算法还需进一步分析。对已有文献而言，针对具体通信模型建立对应的最优化模型，优化目标都是单位数据的能耗，进而分析优化方法，验证算法在实际仿真条件下的正确性。下一步分析重点主要集中在MIMO、OFDM和认知中继能效利用方面。

[1] Mitola J. Cognitive radio architecture evolution: Annals of telecommunications[J]. Annals of Telecommunications,2009,64(7):419-441.

[2] Stotas S,Nallanathan A. Optimal sensing time and power allocation in multiband cognitive radio networks[J].IEEE Transactions on Communications,2011,59(1):226-235.

[3] Wu Y,Tsang D H K. Energy-efficient spectrum sensing and transmission for cognitive radio system[J]. IEEE Communications Letters,2011,15(5):545-547.

[4] Pei Y,Liang Y C,Teh K C,et al. Energy-efficient design of sequentialchannel sensing in cognitive radio networks: optimal sensing strategy,power allocation,and sensing order[J].IEEE Journal on Selected Areas in Communications,2011,29(8):1648-1659.

[5] Shi Z,Teh K,Li K. Energy-Efficient Joint Design of Sensing and Transmission Durations for Protection of Primary User in Cognitive Radio Systems[J].IEEE Communications Letters,2013,17(3):565-568.

[6] Hossain E,Niyato D,Han Z. Dynamic spectrum access and management in cognitive radio networks[M]. London:Cambridge University Press,2009.

[7] Quan Z,Cui S,Sayed A H,et al. Wideband spectrum sensing in cognitive radio networks[C] //Proceedings of 2008 IEEE International Conference on Communications.Beijing:IEEE,2008: 901-906.

[8] Zhao Q. Spectrum opportunity and interference constraint in opportunistic spectrum access[C]//Proceedings of 2007 IEEE International Conference on Acoustics,Speech and Signal Processing.Honolulu,HI:IEEE,2007:605-608.

[9] Jagannathan R. Duality for nonlinear fractional programs[J]. Zeitschrift Fuer Operations Research,1973,17(1): 1-3.

JIANG Zhi was born in Suining,Sichuan Province,in 1984. He received the M.S. degree from University of Electronic Science and Technology of China in 2013. He is now an assistant engineer.His research concerns wireless communication.

Email: szp@uestc.edu.cn

史治平(1972—)，女，河北人，2005年于西南交通大学获博士学位，现为电子科技大学副教授、博士生导师，主要研究方向为纠错编码与无线通信。

SHI Zhi-ping was born in Hebei Province,in 1972. She received the Ph.D. degree from Southwest Jiaotong University in 2005.She is now an associate professor and also the Ph.D. supervisor.Her research concerns error control coding and wireless communication.

Email: szp@uestc.edu.cn

OptimalPowerAllocationofEnergyEfficiencyforMulti-channelCognitiveUsers

JIANG Zhi1,SHI Zhi-ping2

(1.China Academy of Engineering Physics,Mianyang 629100,China;2.National Key Laboratory of Science and Technology on Communications,University of Electronic Science and Technology of China,Chengdu 611731,China)

For the energy efficiency problem of cognitive user with multi-channel,the energy efficiency optimization model is proposed and transmission power and perception time are optimized. Firstly,based on the multi-bandwidth joint energy detection scheme,the multi-channel cognitive user establishes the optimization problem for the target of energy consumption per unit data under certain transmission power and interference power limits. Secondly,the objective function is converted to the form which can be solved by the interior-point method through the dual optimization of the non-linear fractional programming. Thirdly,the algorithm is given by the combination of the interior-point method and the binary search method,and then the optimal power and perception time can be configured. Simulation results show that the proposed optimization method is able to achieve energy efficiency through the optimal configurations of transmission power and perception time corresponding to different communication environment.

cognitive radio；energy efficiency；power allocation；nonlinear fractional programming

10.3969/j.issn.1001-893x.2014.06.023

姜志,史治平.多信道认知用户能量高效的最优功率分配[J].电讯技术，2014,54(6):818-824.[JIANG Zhi,SHI Zhi-ping.Optimal Power Allocation of Energy Efficiency for Multi-channel Cognitive Users[J].Telecommunication Engineering,2014,54(6):818-824.]

2013-11-01；

：2014-03-13 Received date:2013-11-01；Revised date：2014-03-13

：szp@uestc.edu.cnCorrespondingauthor：szp@uestc.edu.cn

TN929.5

：A

：1001-893X(2014)06-0818-07

姜志(1984—)，男，四川遂宁人，2013年于电子科技大学获硕士学位，现为助理工程师，主要研究方向为无线通信；

**