基于拉线位移传感器的动态空间位置测量方法

龚 成，陈文亮，张得礼

(南京航空航天大学 机电学院，江苏 南京 210016)

基于拉线位移传感器的动态空间位置测量方法

龚 成，陈文亮，张得礼

(南京航空航天大学 机电学院，江苏 南京 210016)

通过对动态空间位置测量系统国内外现状的研究，提出了一种基于拉线位移传感器的动态空间位置测量方法，在分析了不同布局形式模型结构特点的基础上，确定了动态空间位置测量系统的布局方式，构建了基于拉线位移传感器的测量系统模型，最后详细阐述了动态空间位置测量系统的组成以及测量方法。

动态空间位置；拉线传感器；测量系统；模型

动态空间位置测量是测量技术的一个新的发展方向，已经成为制造业中的一项重要技术，在航空航天、船舶工业、汽车制造、精密加工、逆向工程等领域占有重要的地位[1-2]。动态测量方法多种多样，其原理也各不相同。由于软、硬件配置，数据类型及数据处理方式不同，不同的测量方式在测量精度、效率和经济性等方面也是千差万别。

针对动态空间位置测量系统，国内外已经展开了广泛的研究：Stephan Spiess.J. R. Mayer等人提出了基于激光跟踪仪的动态空间位置测量方法[3-4]，并对其布局和性能进行了详细分析；赵磊采用了三坐标测量仪进行空间动态测量，并对其动态误差进行了分析[5]。三坐标测量仪能够完成物体的高精度静态测量，但是在测量动态目标的过程中由于其体积、质量较大，易在运动过程中引起运动部件的弯曲变形或使各部件绕气浮导轨连接处发生偏转而产生误差，同时与被测物体紧密接触还会直接影响被测物体的动态特性。目前，动态空间位置测量精度最高的是采用激光跟踪仪实现的，但是由于目前工业机器人特别是小型工业机器人需求量极大，使用频率高且磨损较快，如果均采用激光跟踪仪进行动态测量则成本过高，难以大面积推广。为此，本文提出了一种基于拉线位移传感器的动态空间位置测量系统。

1 测量系统模型建立

测量系统模型的建立以系统运动特性[6]为基础，以测量点的三维空间位置坐标为研究对象，通过能够测量的已知量解算出测量点的空间位置坐标。

1.1布局形式选择

动态空间位置测量系统布局形式的选择是测量系统设计的一个重要方面，它是测量系统的数学模型建立的根本依据，并决定了测量精度以及影响因素，对于空间测量会产生直接的影响。本课题中以拉绳位移传感器为测量基础进行设计，应充分考虑其设计特点与使用要求。

空间位置测量系统的布局形式有多种多样，不同的布局形式均能够实现空间点坐标测量的要求，在这里根据测量底座基准点个数的不同对布局方式进行分类研究，主要可以分为一站法、二站法、三站法以及四站法[7]。

1.1.1一站法

一站法在空间位置测量系统中应用广泛，它以激光跟踪仪为主要代表，该方法在应用的过程中具有测量方便、快捷，模型计算简单等特点。但是一站法在使用过程中不仅需要得到长度量，还需要获得测量基准点与被测点间的两个角度值。

以激光跟踪仪为例，图1所示为一站法的数学模型，O点为测量坐标系的中心点，P点为被测坐标点。通过测量可以得到被测点P的垂直方向角度为α，水平方向角度为β。通过激光跟踪仪可以获得O点至P点的距离为d，则可以假设P点的坐标为(x，y，z)。根据系统模型可以用(α，β，d)直接计算出被测点坐标P的空间位置坐标值，从而得到被测点的空间位置坐标。

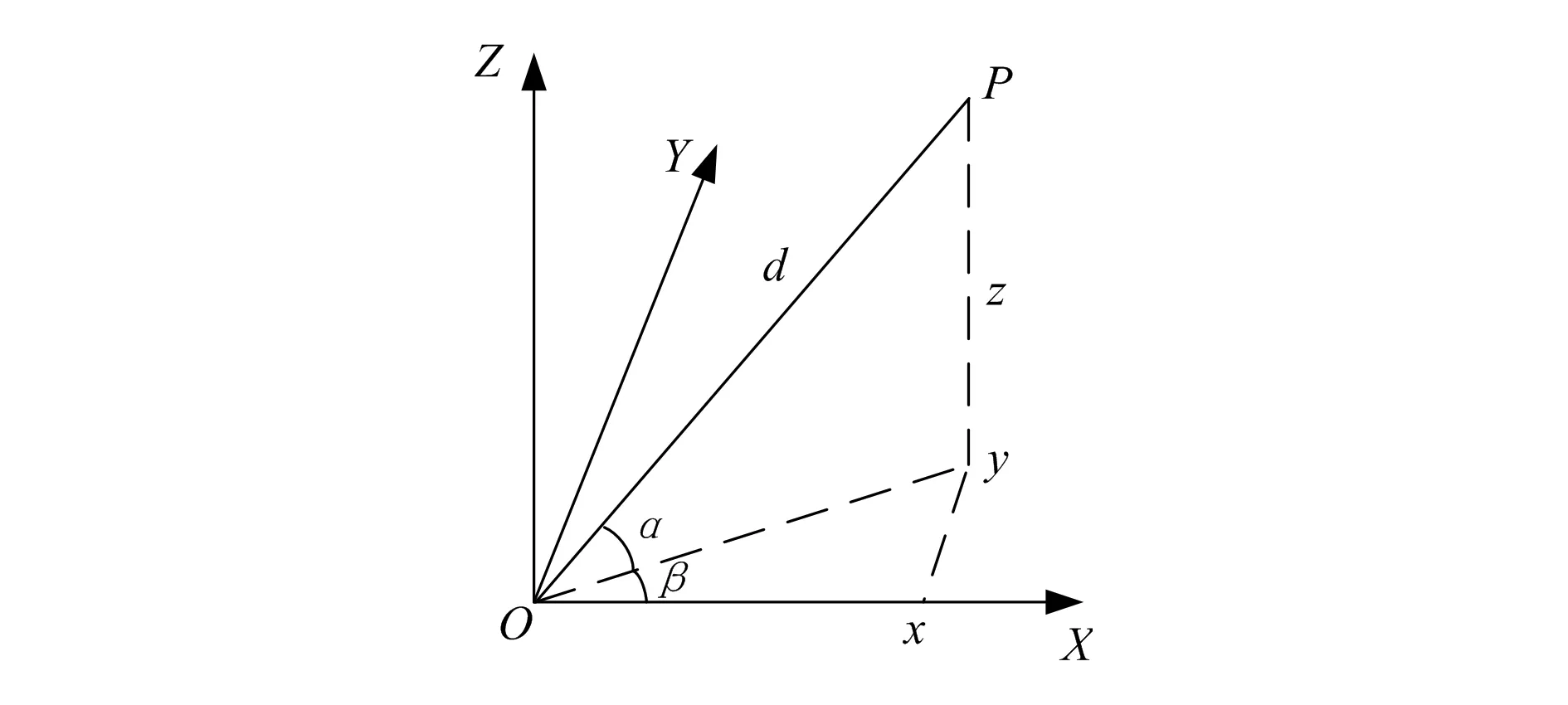
图1 一站法测量数学模型

采用一站法能够快速确定测量点空间位置坐标，测量系统适应性强，只要被测点与基站能够通视即可完成测量，计算过程简单。但是一站法对于距离及角度传感器要求较高，当系统及设备存在误差时难以进行补偿和修正。

1.1.2二站法

二站法也称为三角法，在该测量方法中设有2个测量基准点，与被测目标点构成一个测量三角形，如图2所示。在该测量方法中，通过获得测量点与两基准点的长度L1，L2以及三角平面与基准平面夹角γ即可计算出被测点的位置坐标，或者已知α1，α2，β1，β2，γ也可以计算出空间点的位置坐标。

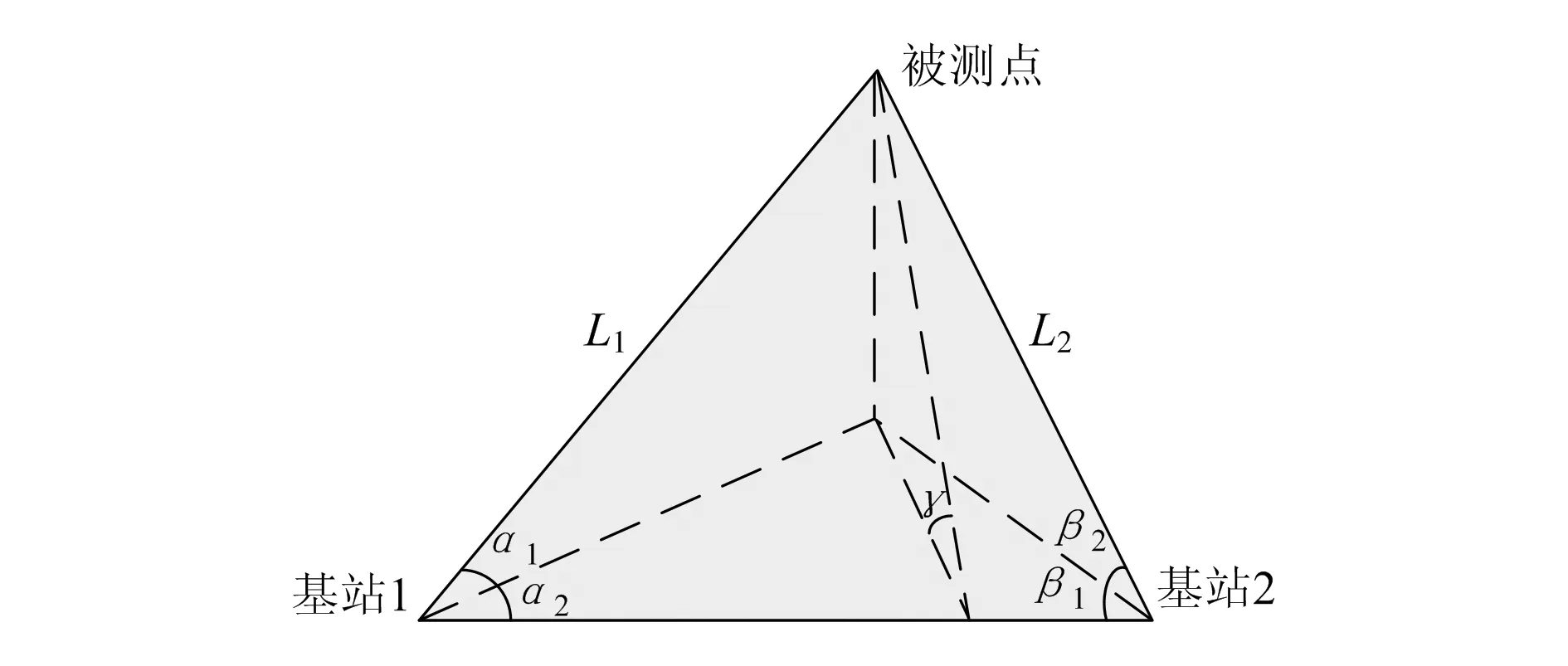
图2 二站法测量模型

1.1.3三站法

三站法即设有3个测量基准点，根据空间模型特点可以知道，根据被测点与空间3个基准点的距离即可获得被测点的唯一确定空间位置坐标。在该种测量方法中仅需要长度量即可获得坐标，无需测量角度量。

三站法测量模型如图3所示，已知3个基准点的位置，再根据3个被测长度量，即可推算出目标点的位置坐标，假定A,B,C分别为3个基准点的测量点，P为被测点。A,B,C的坐标向量(分别表示为r1,r2,r3)已知，而且A,B,C与P的距离(分别为L1,L2,L3)也测量出来，则被测点P的位置坐标向量(用rP表示)可用下式推算出：

(1)

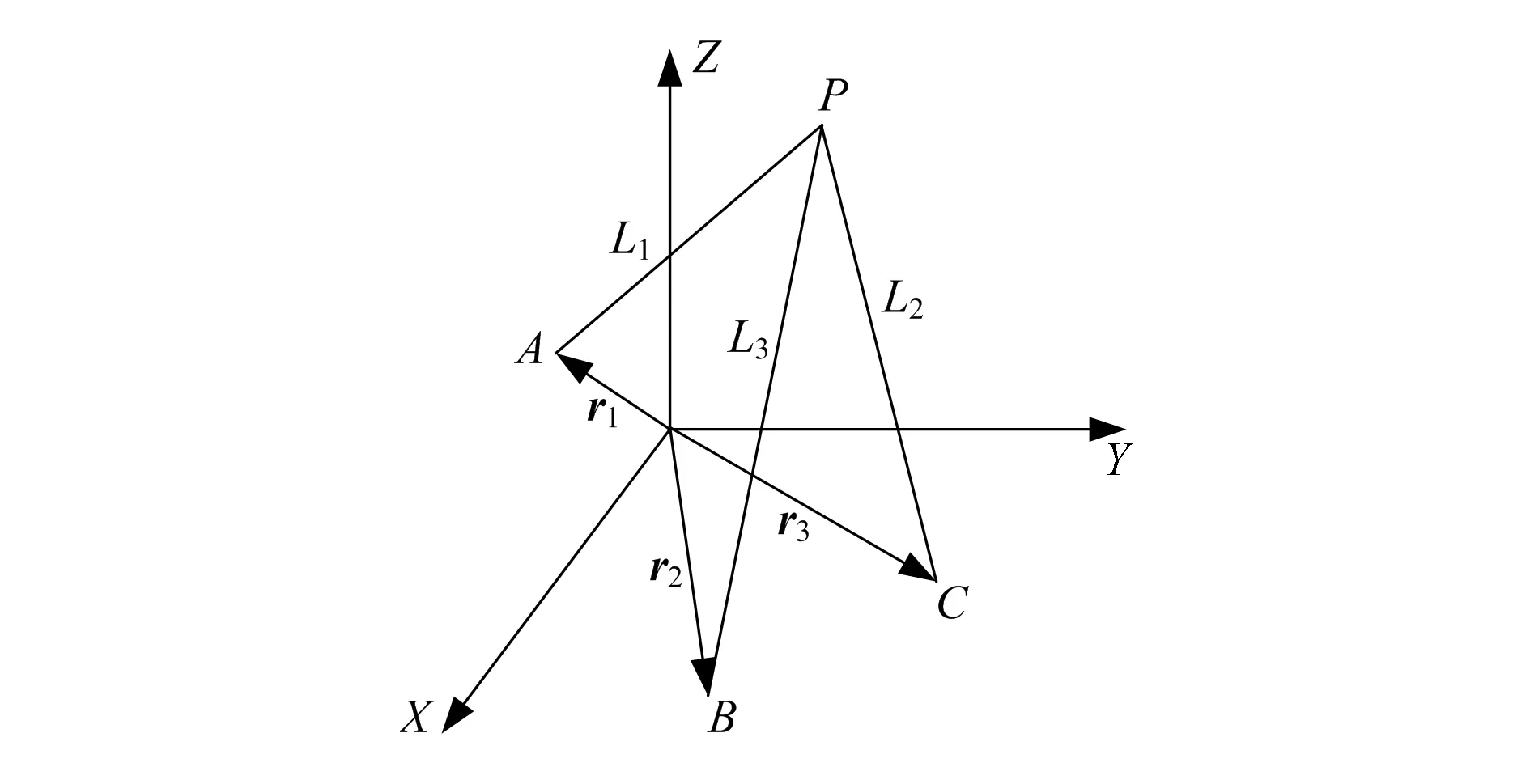
图3 三站测量模型

1.1.4四站法

根据三站法数学模型可以发现，仅需3个长度量即可确定被测点的空间位置坐标，而四站法在使用过程中，在三站法的基础上增加了1个长度量，通过这个量可以对坐标点进行多次运算，从而达到校核被测点的目的，最后可以通过最小二乘法分析该点的空间位置坐标，从而达到提高测量系统精度的目的。四站法的基本方程如下：

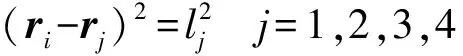
(2)

式中：n是被测点的个数；ri表示第i个被测点的空间坐标向量；lj表示第j个目标点和基准点之间的距离。残差e为：

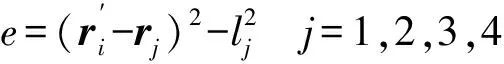
(3)

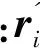
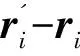
(4)

式(4)可通过标准梯度法(如Gauss-Newton和Levenberg-marquardt)求解。

综上所述，在一站法跟踪测量时，既要测量绝对长度量，又要测量角度量；而三站法只需测量长度量。根据目前传感器特性可知，长度量的测量精度要优于角度量的测量精度。尽管一站法测量数学模型计算简单，测量方便，但是其测量精度没有四站法的测量精度高。针对这一研究结果，动态空间位置测量系统拟采用四站法进行测量。

四站法在使用过程中用3个基站即可获得被测点的空间位置坐标，还有一路冗余数据可以用于对测量结果进行修正。通过测量结果辨别误差最大的数据进行修正，从而获得补偿后的空间位置坐标，相比其他布局方式既能简化系统模型及数据处理过程，又能满足系统的使用精度及可靠性。

1.2测量系统模型建立

在空间位置测量系统中，所有的被测特征的定义、测量过程的控制都是在一定坐标系下进行的，常用的坐标系一般有直角坐标系、圆柱坐标系和球坐标系[8]，为便于后期显示及对动态性能求解，本文选择建立三维直角坐标系，测量系统模型如图4所示。

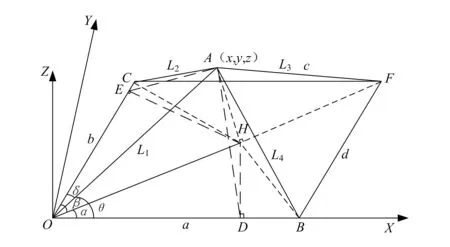
图4 测量系统模型

该系统模型中含有4个由拉线传感器组成的长度测量单元，分别放置在O,B,F,C4个位置。现以O点为坐标系原点构建三维直角坐标系，OB边为X轴，过O点并垂直于OB方向为Y轴，根据右手定则,垂直于XOY面向上为Z轴,建立三维直角坐标系，假设各点、长度及角度标注如图4所示。4个测量单元的测量线通过连接转换器最终可汇集到空间同一点A，被测点A坐标假设为(x,y,z)，即可获得测量系统模型如下：

式中:a,b,c,d分别为OB，OC，CF，BF边长度，该长度可通过实验模型直接测量获得;L1，L2，L3，L4分别为拉绳AO，AC，AF，AB的长度，该长度需要通过拉线传感器实际测量获得;角度值α,β,θ,δ需要通过模型坐标计算得到。由于三组测量值即可确定一组数据，故可先选取L1，L2，L3进行计算，获得α,β的主要计算过程如下：

在△AOB中，角度θ为：

(5)

在△AOC中，角度δ为：

(6)

在△AOD中，由于OD垂直于AD,则

x=OD=L1·cosθ=L1·

(7)

在图4中可假设

(8)

将式(5)和式(6)代入式(8)可得

(9)

根据几何模型可知

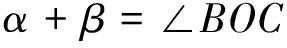
(10)

∠BOC值可通过系统初始化测量解算得到

(11)

根据三角余弦公式可知：

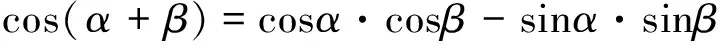
(12)

将式(8)代入式(12)中，得：

求解可得：

通过解算可以获得角度α值，因此可得到被测点各坐标分别为：

通过上述计算可以得到被测点A在O-XYZ坐标系中的空间坐标位置[9]，即测量系统模型。

2 动态空间位置测量系统

动态空间位置测量系统主要由以下部分构成：(1)4个高精度拉绳位移传感器；(2)4个传感器安装底座；(3)测量点的连接转换器；(4)数据采集系统；(5)数据分析及显示系统。传感器分布于底座4个端点上，为便于后期坐标变换和处理，将每2个传感器固定于同一轴线上且以反方向放置。连接转换器可安装在被测设备上，用于连接测量所用的传感器拉绳测量端，同时将拉绳方向汇集到测量点，便于后期计算与处理，系统简图如图5所示。

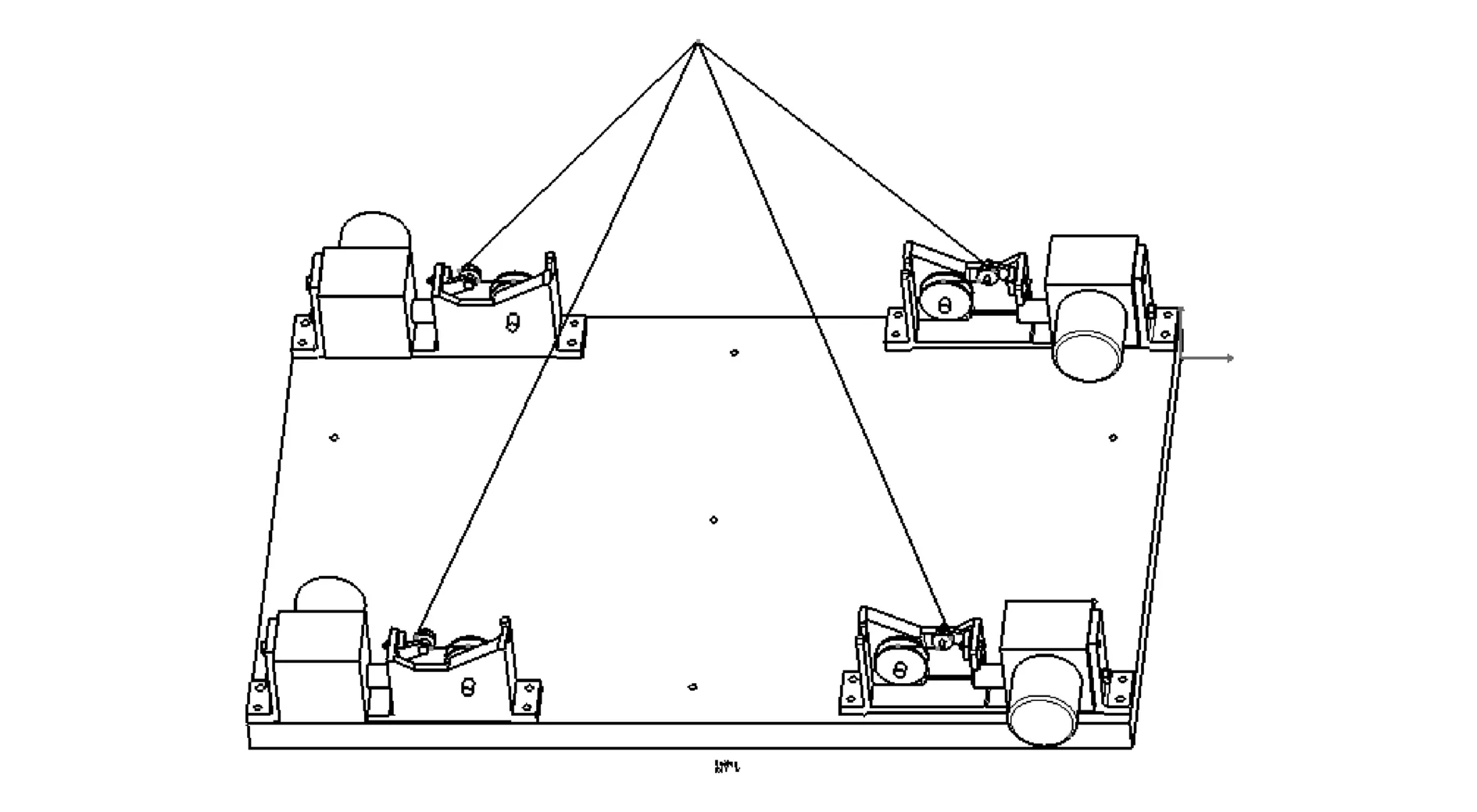
图5 动态空间测量系统简图

基于拉线位移传感器的动态空间位置测量系统在使用的过程中需要充分了解其使用特性[10]，严格按照使用步骤和要求进行操作，以确保测量过程的高精度和高效率。

在测量系统使用过程中，应首先对系统进行初始化标定，从而消除测量系统的系统误差，确定测量系统空间坐标系，完成系统初始化定义。标定的内容主要包括两部分，首先是单个测量单元的标定，其次是测量系统整体测量结果的标定。

测量单元的标定是指通过测量单元上专门设计的标定工艺孔来进行测量单元的标定，通过标定过程可以推算拉线位移传感器在“零位”时的数据，只有完成测量单元工艺零点的标定，才能够获得测量单元在实际测量过程中拉线位移的长度,即拉线伸出量。

单个测量单元的初始化标定示意如图6所示，测量所用的拉线通过导向滑轮引出，并通过标定连接器连接至测量端。在标定的过程中，将拉线上连接的标定连接器的标定表面与标定孔对接，这两个表面和尺寸在设计过程中有着严格的装配公差和表面光洁度要求，以保证拉线能够沿滑轮上切线通过标定孔中心。这样即可获得测量单元的初始长度位置，从而可以在后期的测量过程中获得拉线的精确长度并解算位置坐标。

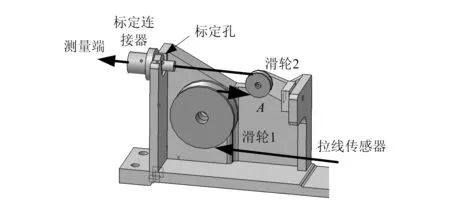
图6 测量单元标定简图

完成单个测量单元的标定之后则要进行测量系统的初始化标定，在标定过程中主要依据标准测量孔，通过标准板(图7)所测量的相对位置数据关系对测量系统进行初始化修正。

图7 标定标准板

标定标准板上设计有4排间隔相等、直径为4mm的精密孔，孔的大小与标准4mm测量头构成间隙配合。利用标定标准板对测量系统进行标定，可以通过高精度的标准头对标准板上的孔位进行测量，获得其孔位的相对位置关系及其标准值，通过对比其真实值来获取测量系统的系统误差。最后通过对系统误差的研究和分析，对测量系统进行合理的误差修正和补偿，完成测量系统测试前的标定。完成标定工作后即可将测量头安装于被测设备上进行动态空间位置测量，测量系统将会实时获取传感器数据，并计算出动态坐标以及测量点的速度、方向等动态数据。

3 结论

使用本文中设计的动态空间位置测量系统，已经能够通过测量多段距离实现被测目标点坐标的确定。虽然通过实验证明了该模型的有效性和可行性，但在后期工程实际中还需要考虑环境、温度等外界因素的影响[11]，提高系统使用精度。基于拉线位移传感器的动态空间位置测量系统是一种简单方便且灵活的坐标测量系统，不仅可以快速获得被测物体的静态坐标，而且还能实时获取被测目标的运动速度、方向以及加速度等动态特性参数，对于工业设备的运动及动力学特性分析有着重要意义。

[1] 陈晓荣，蔡萍，施文康，等.激光跟踪运动物体空间坐标测量系统研究[J].仪器仪表学报，2004，25(6):777-780.

[2] JUDD R P，KNASINSKI A. A technique to calibrate industrial robots with experimental verification[J]. IEEE Trans on Robotics & Automation，1990,6(1): 20-30.

[3] 赵磊，杨杰. 基于Solidworks Simulation的三坐标测量仪动态误差分析[J]. 机床与液压，2012，40(1):39-42.

[4] STEPHAN S, MARKUS V, MINU A. On the calibration of a 6-D laser tracking system for dynamic robot measurements[J]. IEEE Trans.Instru.Meas，1998, 47 (1) :270-274.

[5] MAYER J，GRAHAM A，PARKER. Aportable instrument for 3-D dynamic robot measurements using triangulation and laser tracking[J].IEEE Trans. Robot. Auto, 1994，10 (4) : 504-516.

[6] 杨恢，田一明，赵幸福，等. 复杂装配环境中数字测量坐标体系的构建[ J ].船海工程，2012，41(1)：10-13.

[7] 刘永东，王佳，梁晋文. 运动目标空间位置坐标激光跟踪测量的数学模型[J]. 光学技术，1997，23(6):31-34.

[8] 王佳,胡朝晖,刘永东,等. 激光跟踪虚拟坐标测量系统与自标定方法的实验研究[J]. 光学技术，2001，27(5):447-450.

[9] 王武义,徐定杰,陈健翼.误差原理与数据处理[M]. 哈尔滨：哈尔滨工业大学出版社,2001.

[10] 王兴,戚景观.一种新的拉线式位移传感器的设计及其应用[J].机械工程与自动化，2012(4):171-173.

[11] 张富春,张军,许文海，等. 激光跟踪仪现场测量不确定度的评定[J]. 计量学报, 2005, 26 (1):20-22.

TheDynamicSpatialPositionMeasurementMethodBasedonLineDisplacementSensor

GONG Cheng, CHEN Wenliang, ZHANG Deli

(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)

It presents a measurement method for dynamic spatial position based on line displacement sensor. Based on the comparison about structural characteristics between different layouts, it determines the layout of our measurement system, establishes the model of measurement system based on line displacement sensor, and elaborates the structural and measurement method of the dynamic spatial position.

Dynamic Spatial Position; Line Displacement Sensor; Measurement System; Model

10.3969/j.issn.2095-509X.2014.03.015

2014-01-02

龚成(1987—)，男，湖北洪湖人，南京航空航天大学硕士研究生，主要研究方向为飞机装配技术。

TH721

A

2095-509X(2014)03-0057-05