一种基于RFID的制造车间实时定位算法研究

闫振强，郭 宇，张小瑞，年丽云

(南京航空航天大学 机电学院，江苏 南京 210016)

一种基于RFID的制造车间实时定位算法研究

闫振强，郭 宇，张小瑞，年丽云

(南京航空航天大学 机电学院，江苏 南京 210016)

针对LANDMARC系统在制造车间定位应用中存在的问题，提出一种基于RFID的制造车间实时定位改进算法。从研究基于LANDMARC系统的制造车间定位技术入手，深入分析了系统在实施过程中存在的问题，重点阐述了改进最佳邻居算法的定位流程及关键模块设计，最后在搭建的实验室模拟环境中进行了定位测试。测试结果表明，改进算法的平均定位误差可以达到0.5m，定位精度对比LANDMARC算法提高了20%，能够很好地适应实验室模拟环境。

制造车间；RFID定位；LANDMARC系统；最小二乘曲线拟合

随着车间物联网的深入开展，车间对象的实时定位管理已经成为车间信息管理的重要组成部分，面向制造车间的室内定位服务研究也越来越受到社会各界的关注[1]。

典型的室内定位技术主要包括红外线定位、A-GPS定位、超声波定位、UWB定位以及基于RSSI的无线射频定位等方法[2-3]。其中，RFID技术以其非接触双向通信、适应能力强、可多标签同时识别、抗干扰能力强、操作方便以及成本较低等优点，已经成为室内定位的优选技术。采用RFID技术的LANDMARC定位系统[4]捕捉“最佳邻居”参考标签，并由“最佳邻居”参考标签权重确定待测标签的位置坐标，定位精度高，得到了广泛的应用。LANDMARC定位系统为保证定位精度，需要大面积铺设参考标签，这必将引入参考标签之间的射频干扰，定位系统的实时性也无法保障；此外实验还表明，LANDMARC系统对处在参考标签覆盖区域边界的待测标签的定位效果也不理想[5-6]

针对这些情况，基于LANDMARC的改进算法也相继被提出，李军怀等学者[7]提出虚拟参考标签空间定位算法，能够有效降低部署密集的参考标签处的射频干扰，缺点是计算繁琐，实时性差；朱剑等学者[8]用三角法计算待测标签的预估位置，一定程度上提高了系统的实时性能，但需要增设硬件设备；史伟光等[9]提出了一种基于噪声分析的加权欧式因子改进算法，改善了对区域边界待测标签的定位性能，难点在于算法中最优置信阶数的确定。因此，针对LANDMARC系统在制造车间应用中存在的不足，从研究基于LANDMARC系统的车间实时定位技术入手，提出了融合最小二乘曲线拟合的改进型LANDMARC算法，以满足车间实时定位的需要。

1 基于LANDMARC系统的车间实时定位技术研究

车间物联网是基于车间对象的自动识别展开的车间感知网络。感知网络得以建立就必须满足以下两个条件：(1)制造车间各类生产要素都以某种特定方式附着RFID标签；(2)车间RFID读写器等感知设备的按需布置。基于LANDMARC定位系统，绘制制造车间定位场景示意图，如图1所示。

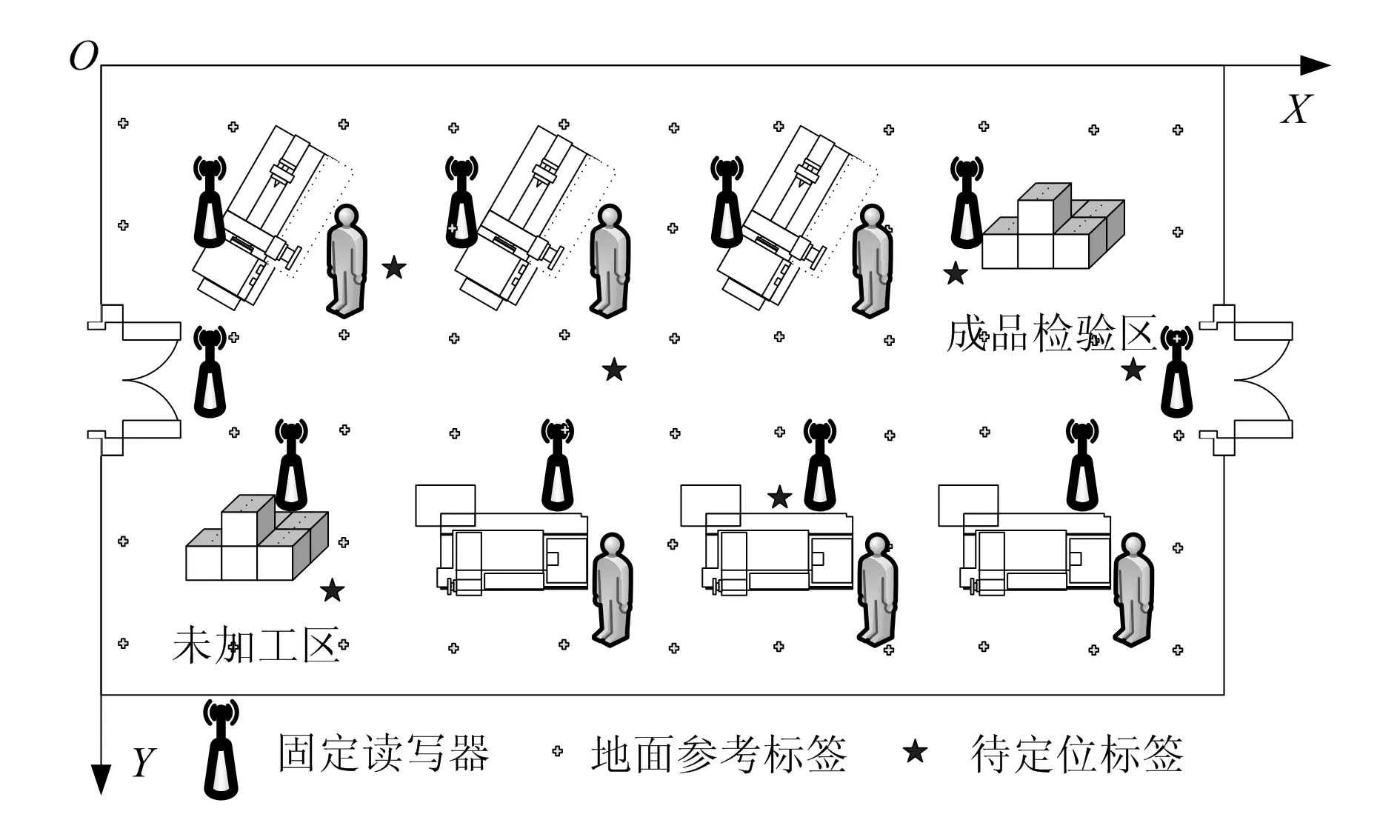
图1 制造车间定位场景示意图

在制造车间内部，参考标签以0.6m的间隔分别沿水平和垂直方向均匀附着在车间地面，作为定位的参考节点；固定式读写器以车间工位为单位，在车床区、铣床区、成品待检区以及未加工区分别布置，另外部署2台于出入口处，主要负责记录物料的入库及成品的出库；待测标签以某种特定的方式附着于车间生产要素，并跟随车间对象生产工艺流动。

LANDMARC算法是一种基于读写器接收到标签电磁波能量大小(RSSI)的伪测距定位算法，该算法将位置坐标已知的参考标签作为参照节点，通过比较待测标签与之的RSSI差值，捕捉到待测标签的最近邻居标签，并根据此差值计算出最近邻居标签相对于待测标签的位置权重，最后利用质心法求得待测标签的位置坐标。

在车间实时定位实际应用中，基于LANDMARC的定位系统还存在一些问题：

a.人为部署参考标签，缺乏理论性指导，可能致使LANDMARC算法不能“收敛”，最终导致无法得出定位结果。

b.LANDMARC算法的数据源稳定性差，制造车间环境复杂，电磁干扰严重，很容易导致多径效应、空间场强分布不均以及不可测信号干扰事件的发生，LANDMARC算法中并没有针对这些问题给出具体的解决方案。

c.LANDMARC算法的定位时间冗余，LANDMARC系统在寻找最近邻居参考标签时，算法认定所有的参考标签为最近邻居的候选标签，计算待测标签与任意参考标签的欧几里德距离，然后逐个比较相关度值，最终确定最近邻居参考标签。实际上，在寻找最近邻居标签时，距离待测标签较远的参考标签必将被排除，它们的引入非但不能提高定位的精确度，反而对最近邻居的筛选构成干扰，并在很大程度上降低了系统的实时性能。

d.LANDMARC算法中最近邻居个数k-nearest的选取具有无法克服的盲目性。

制造车间定位环境时刻处于动态变化之中，这种动态改变除了包括人员以及AGV小车的随机流动之外，还存在着在制品的工艺流动、物料的入库以及成品的检验出库等非静态情况。动态的变化环境必然会影响算法对最近邻居参考标签的选择，显然静态k-nearest值的定位算法已经不能满足车间定位的准确性和稳定性要求。

2 改进的最佳邻居算法

针对LANDMARC系统在制造车间定位应用中存在的问题，本文提出一种融合了最小二乘曲线拟合算法与LANDMARC算法的最佳邻居算法。

本文提出的最佳邻居算法的定位基本流程如图2所示。

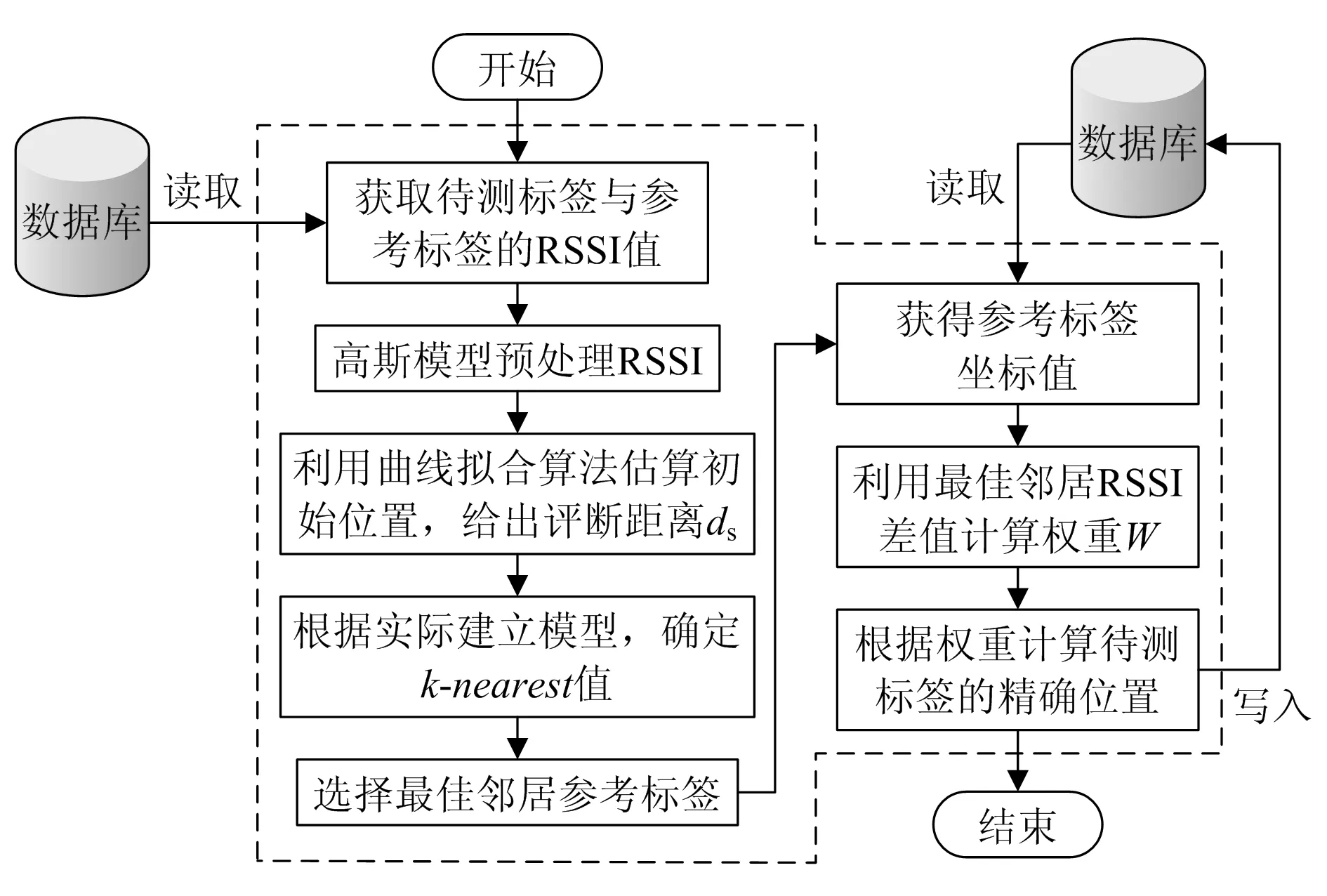
图2 最佳邻居算法定位流程图

2.1高斯模型处理RSSI

高斯模型以出现的概率大小为依据进行数据处理。在同一位置不同时刻，读写器可能接收到n个不同的RSSI值，其中必然存在着小概率事件。通过设定临界点，高斯模型筛选出高概率发生区域对应的RSSI值，将其几何平均值作为定位依据，能够有效地降低小概率、大干扰因素对测量的影响，提高定位依据的准确性。

普遍采用的RSSI室内路径损耗模型为[10]：

(1)

式中：d0为近地面参考距离，由实验测试获得；p0是距离为d0时测得的信号强度；p是读写器距离标签d时测得的信号强度；n表示路径损耗指数，随周围环境变化而变化；ζ为遮蔽因子，ζ～N(m,σ)。

由式(1)可知，实际测得的p也服从高斯分布。本文在每个距离点上分别采集500次RSSI值，取0.6作为临界值，选择高斯分布函数值大于0.6对应的RSSI值。

2.2最小二乘曲线拟合

定义λij(i=1,2,…,k;j=1,2,…,n)表示第i个读写器所测得的第j个参考标签的RSSI值，记做xi。

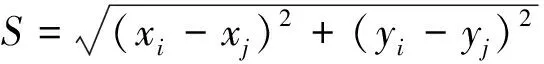
本文取θ=span{1,x,x2,…,xn}，多项式拟合的法方程为：

至此可求出基于(m+1)个RSSI值的最小二乘拟合多项式s(x)。为了便于计算，这里取n=3，二次多项式曲线拟合误差可由下式计算

解如下方程组即可求得待测标签的初始坐标(x,y)。

计算初始位置与参考标签的距离，结合定位误差设定评断距离ds。

2.3k-nearest值自适应

在复杂的制造车间环境下，读写器被障碍物所隔挡的情况极为普遍，实际模型如图3所示。

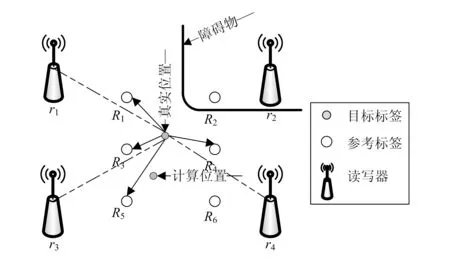
图3 障碍物隔挡情况下的实际模型

模型中障碍物将参考标签R2和读写器r2隔离，相当于读写器r2不能正常工作，参考标签R2也无法参与计算。在这种情况下，按照经典的LANDMARC算法，取固定值k-nearest=4，待测标签的区域就不再是由R1R2R3R4围成的一个矩形区域，而是由R1R3R4R5围成的一个多边形区域。显然，按照此算法计算得到的待测标签位置与其真实位置相比将会有很大偏差。

针对以上问题，本文抽象出读写器与待测标签两种关联关系，包括正常工作关系和设备故障关系，并设置标志位p作为读写器的新增属性，通过检测标志位p来判断读写器的工作状态；当读写器能够监测到待测标签并返回标签RSSI值时，两者视为正常工作关系，此时令p=1；否则均视为设备故障关系，令p=0。假定处于待测标签感知区域的正常工作的读写器个数为n，如果n<4，则最近邻居标签个数k-nearest=3，否则k-nearest=4。

2.4最近参考标签选取及坐标计算

按照图1所示的参考标签部署示意图，在某区域部署m个随机分布的待测标签、k个固定式阅读器以及n个均匀分布的参考标签。定义参考标签信号强度矩阵λ：

定义待测标签信号强度矩阵f：

第i个读写器测得的参考标签与待测标签之间的场强差矩阵为：

式中：rinm=|fin-λim|表示第i个读写器测到的第n个参考标签与第m个待测标签的场强差,i=1,2,…,k。比较每列的场强差，将超出评断距离的参考标签与待测标签的场强差值设为inf(无穷大数)，可以求得第i个读写器获得的最近邻居标签矩阵为：

定义Aij=(ri1j,ri2j,ri3j,…,inf)T表示第i个读写器测得第j个待测标签的最近邻居标签，确定出第j个待测标签的所有最近邻居标签矩阵为Tj=(A1j,A2j,Akj)。假设ui为第i个读写器选定的最近邻居参考标签个数，那么第j个待测标签所有最近邻居参考标签个数为w=u1+u2+…+uk。待测标签u与参考标签的距离关系可以由相关度矩阵D*表示：

待测标签的坐标可由下式求得：

式中：k-nearest表示最佳邻居参考标签的个数，这里取k-nearest=3；(xi,yi)表示待测标签u的最佳邻居参考标签的坐标；wi表示第i个参考标签在k-nearest个最近邻居参考标签中所占的权重。

定义定位误差为：

(2)

式中：(x0,y0)是待测标签的实际位置坐标；(xt,yt)是改进定位算法给出的待测标签坐标。

3 实验结果及分析

本文实验的主要内容包括基于LANDMARC的最优邻居算法性能测试和对正三角形参考标签部署优化两个方面，为保证测试的有效性及实验结果的可信度，测试在能够模拟车间环境的实验室内部进行。

实验室环境下定位测试场景如图4所示。

图4 实验室环境下定位测试图

环境中包括模拟制造车间环境的桌椅、若干障碍物等，定位测试区域20m×6m，参考标签按照一定的规则均匀铺设在实验室地面，待测标签随机分布，8个天线的位置坐标为L1(0,0)、L2(0,7)、L3(0,13)、L4(0,20)、L5(10,0)、L6(10,7)、L7(10,13)、L8(10,20)。图中，R表示两个XCRF-860读写器；A代表待测标签，由于实物图空间关系，未全部标出；antenna表示组成定位网络的读写器天线。

选定某一个待测标签M，对区域内的50个位置进行定位测试，每个位置测试10次，根据式(2)计算每个位置的平均定位误差(ALE)。基于改进的最近邻居算法，待测标签M的平均误差如图5所示。

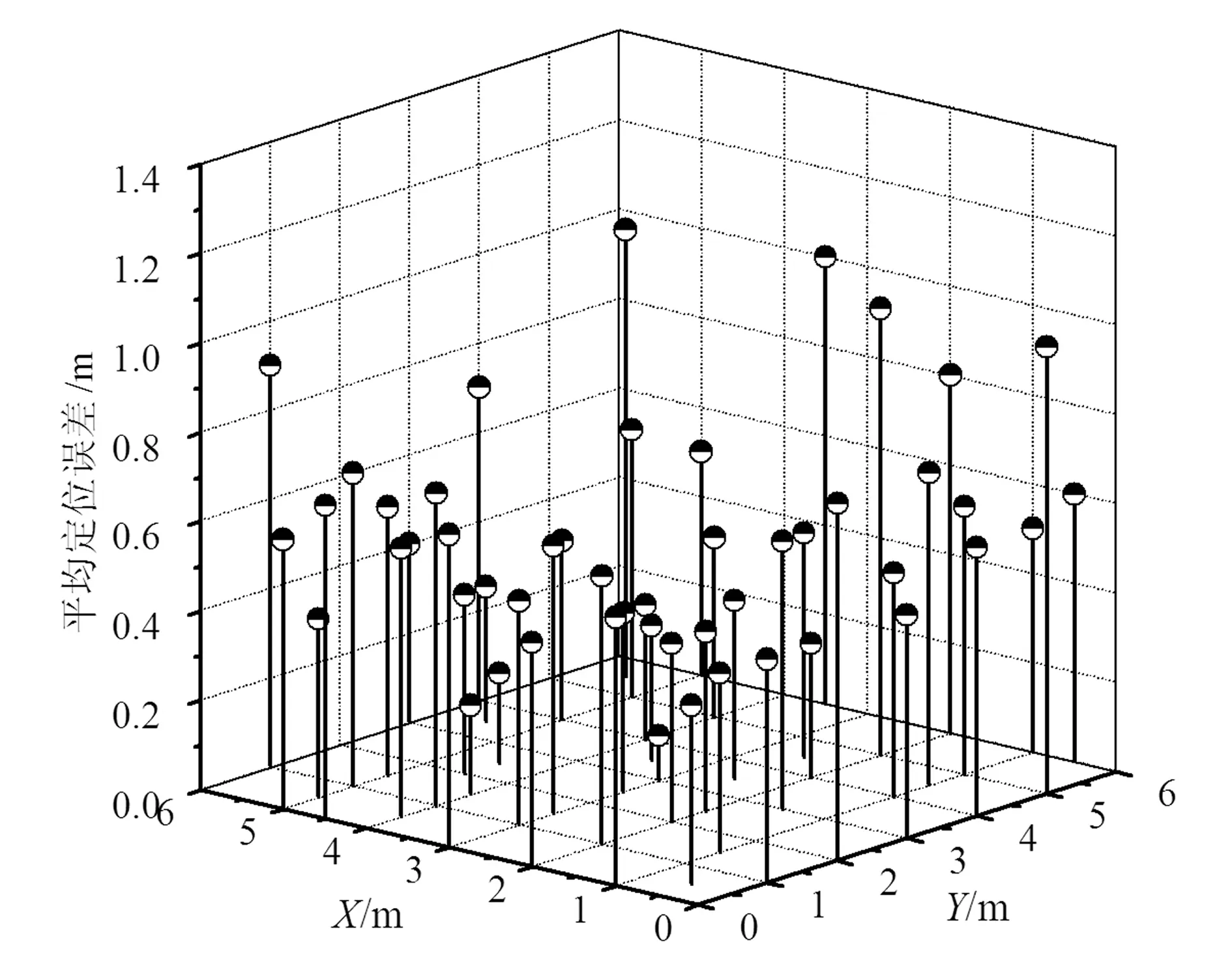
图5 待测标签M在不同放置位置处测得的平均误差

对区域内随机分布的10个待测标签各测试10次，并记录平均定位误差，3种算法的对比见表1。

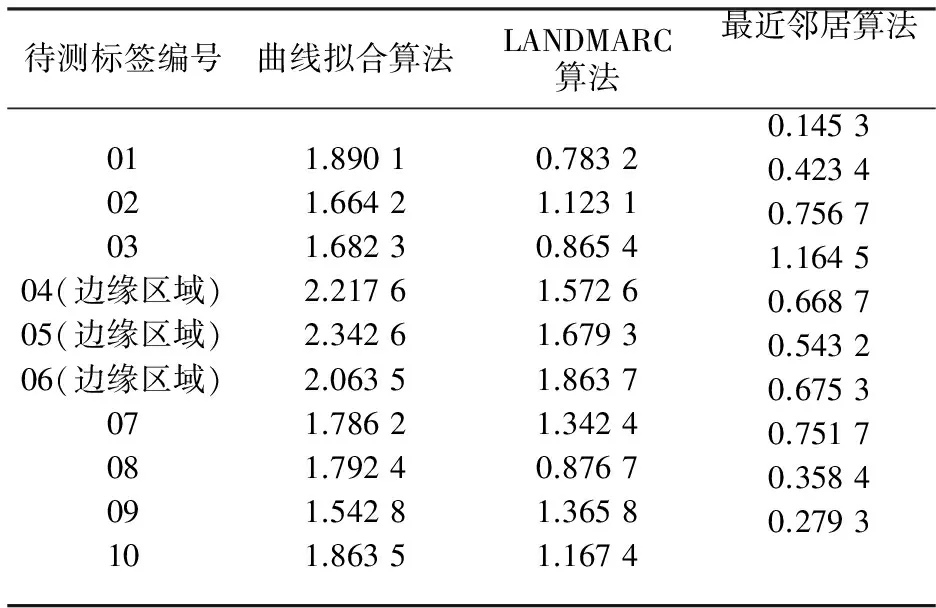
表1 3种定位算法平均误差比较

由表1可知：曲线拟合定位算法的定位效果最差，最大平均定位误差为2.764 2m，最小平均定位误差为1.542 8m；LANDMARC算法定位效果稍好，最大平均定位误差降低了30%，最小平均定位误差降低了45%；最佳邻居算法的最小平均定位误差缩小为0.145 3m，最大平均定位误差为1.164 5m，处于参考标签边缘区域与中心区域的待测标签的定位性能差距明显缩小。

参考标签的优化部署也是LANDMARC算法改进的一部分，在最优邻居算法定位的过程中，以正三角形的部署方式取代传统的矩形网络部署方案。为了进一步验证正三角形部署的优越性，设定了如下对比实验：在参考标签数量、选定的待测标签和放置位置均保持不变的前提下，分别基于LANDMARC和改进算法进行定位，每个位置处测试10次，得到的平均定位误差对比图如图6所示。

图6 正三角形部署与矩形部署误差对比

由图6可以看出，在参考标签正三角形部署的情况下，采用改进型算法，比矩形部署情况下的平均定位误差减小了7.4%；采用LANDMARC算法，与矩形部署情况下的平均定位误差减小了5.2%，由此可知，参考标签的正三角形部署对两种算法的定位精度均有提高。

4 结束语

本文通过分析LANDMARC定位系统在制造车间应用中存在的问题，提出了一种融合了最小二乘曲线拟合算法的改进最佳邻居算法。实验测试表明，该算法能够很好地适应实验室模拟环境，对于在定位精度与稳定性方面都有较高要求的制造车间环境中的应用具有现实意义与参考价值。

[1] Hu Ping, Wang Lei, Lu Jingui，et al.Improved strategy of genetic algorithm for optimum location of radio frequency Iidentification reader[J].Sensor Letters,2012,10(8):1897-1901.

[2] 杨东勇,顾东袁,傅晓婕，等.一种基于RSSI相似度的室内定位算法[J].传感技术学报,2009,22(2):264-268.

[3] 顾嘉,钱钰博,孙厚芳，等.工装室内定位技术研究[J].北京理工大学学报,2010,30(9):1056-1058.

[4] 王远哲,毛陆虹,刘辉，等.基于参考标签的射频识别定位算法研究与应用[J].通信学报,2010,31(2):86-92.

[5] Lu Jingui, Li Hongliang, Chen Fengxin，et al.Combining strategy of genetic algorithm and particle swarm algorithm for optimum problem of RFID reader[J].International Journal of Innovative Computing and Applications,2011,3(2):71-76.

[6] Galiotto Carlo, Marchetti Nicola, Prasad Neeli，et al.Low access delay anti-collision algorithm for readers in passive RFID systems[J].Wireless Personal Communications,2012,64(1):169-183.

[7] 李军怀,孙转宜,王一乐，等.基于虚拟参考标签的RFID定位系统构建方法[J].计算机科学,2011,38(4):107-110.

[8] 朱剑,赵海,孙佩刚，等.基于RSSI均值的等边三角形定位算法[J].东北大学学报：自然科学版,2007,28(8):1094-1097.

[9] 史伟光,刘开华,于洁潇，等.基于加权欧式算子的射频识别定位算法[J].计算机工程,2011,37(9):22-24,28.

ARealTimePositioningAlgorithmforManufacturingWorkshopBasedonRFID

YAN Zhenqiang, GUO Yu, ZHANG Xiaorui, NIAN Linyun

(Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China)

Aiming at the defects of LANDMARC algorithm applied in manufacturing workshop, it puts forward a kind of improved localization algorithm based on RFID for manufacturing workshop object localization. It introduces the positioning technology for manufacturing workshop based on LANDMARC. Based on in-depth analysis of the deficiencies of the algorithm, it represents the best neighbor algorithm of localization process and the key module design, develops a localization testing in the building of laboratory simulation environment. Test results show that the algorithm of minimum average position error can reach 0.1 m, and increase the positioning accuracy 20% compared with LANDMARC algorithm, and be adaptable for the laboratory simulation environment.

Manufacturing Shop; RFID Positioning; LANDMARC System; Least-squares Curve Fitting

10.3969/j.issn.2095-509X.2014.03.014

2013-12-30

国防基础科研项目(A2520110003)

闫振强(1987—)，男，河南安阳人，南京航空航天大学硕士研究生，主要从事数字化设计与制造、物联网技术、RFID定位等研究。

TP39

A

2095-509X(2014)03-0052-05