约束阻尼板结构振动声辐射优化

郑 玲, 祝乔飞

(重庆大学 机械传动国家重点实验室，重庆 400044)

尽管主动振动噪声控制能有效抑制结构的低频噪声，但低噪声设计以其优异的性能和可靠性而备受关注。Kikuchi[1]首先将拓扑优化方法应用于结构低噪声设计，通过材料布局优化，实现了结构低噪声设计。Luo等[2]采用拓扑优化方法，通过对封闭结构的优化，大大降低了封闭结构内部的声辐射。Baz等[3]采用有限元法，建立了板-声腔耦合动力学模型，以声腔模态频率峰值声压最小化为目标函数，对板的材料布局进行了拓扑优化设计，实验验证了理论分析结果的正确性。对结构表面进行阻尼处理，能有效降低结构的振动与声辐射，广泛应用于航空、航天、汽车及船舶等领域。阻尼结构可分为自由阻尼和约束层阻尼，相比自由阻尼，约束层阻尼消耗的能量更多，减振作用更大。

如何根据结构的动力学特性要求，确定阻尼材料的最优布局，是阻尼结构设计的一个关键问题。郭中泽等[4]采用渐进结构拓扑优化方法，以结构模态损耗因子最大化为目标，研究了阻尼结构设计中阻尼材料的最优分布问题。杨德庆等[5]采用均匀化拓扑优化方法，以薄板模态频率最大化为目标，研究了薄板的最优材料布局问题。李以农等[6]采用渐进结构拓扑优化算法，以结构模态阻尼比最大化为目标函数，研究了约束层阻尼梁的阻尼材料最优分布问题。郑玲等[7]建立了约束阻尼板的有限元模型，推导了模态阻尼比对单元胞位置的灵敏度，提出了一种基于进化方式的约束阻尼优化布局方法。李超等[8]研究了圆柱壳体上阻尼材料的最优分布问题。王明旭等[9]将变密度法引入阻尼材料的布局设计，推导了灵敏度表达式，提出了模态振型的跟踪方法。吕毅宁等[10]给出了附加自由阻尼复杂结构的有限元建模方法，以结构的动态柔度最小化为目标函数，计算了薄板和车身地板附加自由阻尼的拓扑优化布局。以上文献均以结构振动损耗因子、固有频率或动柔度为目标函数，采用拓扑优化方法，研究了阻尼材料的最优布局。

在某些特殊环境下，结构振动导致的声辐射更为人们所关注，如潜艇的结构静音设计、飞机或汽车舱内噪声的控制等。目前，以声压或声功率等声学性能为目标函数，采用拓扑优化方法，对结构进行优化已有大量研究。Sigmund等[11]将拓扑优化方法应用于室内声学设计和噪声屏蔽墙设计，对比了优化前后的材料布局与声压均方值变化。Sun等[12]建立了蜂窝夹层梁的有限元模型，以特定频率辐射声功率最小化为目标函数，对蜂窝的形状及尺寸进行了优化。但是，采用拓扑优化方法，以辐射声功率最小化为目标，对约束阻尼材料布局进行优化的研究尚不多见。

本文首先建立四边简支约束层阻尼板有限元模型，用Rayleigh积分推导结构辐射声功率，并进行灵敏度分析，以声功率最小化为目标函数，采用渐进优化算法，对约束阻尼材料布局进行优化。

1 约束层阻尼板振动和声辐射计算

1.1 约束层阻尼板有限元模型

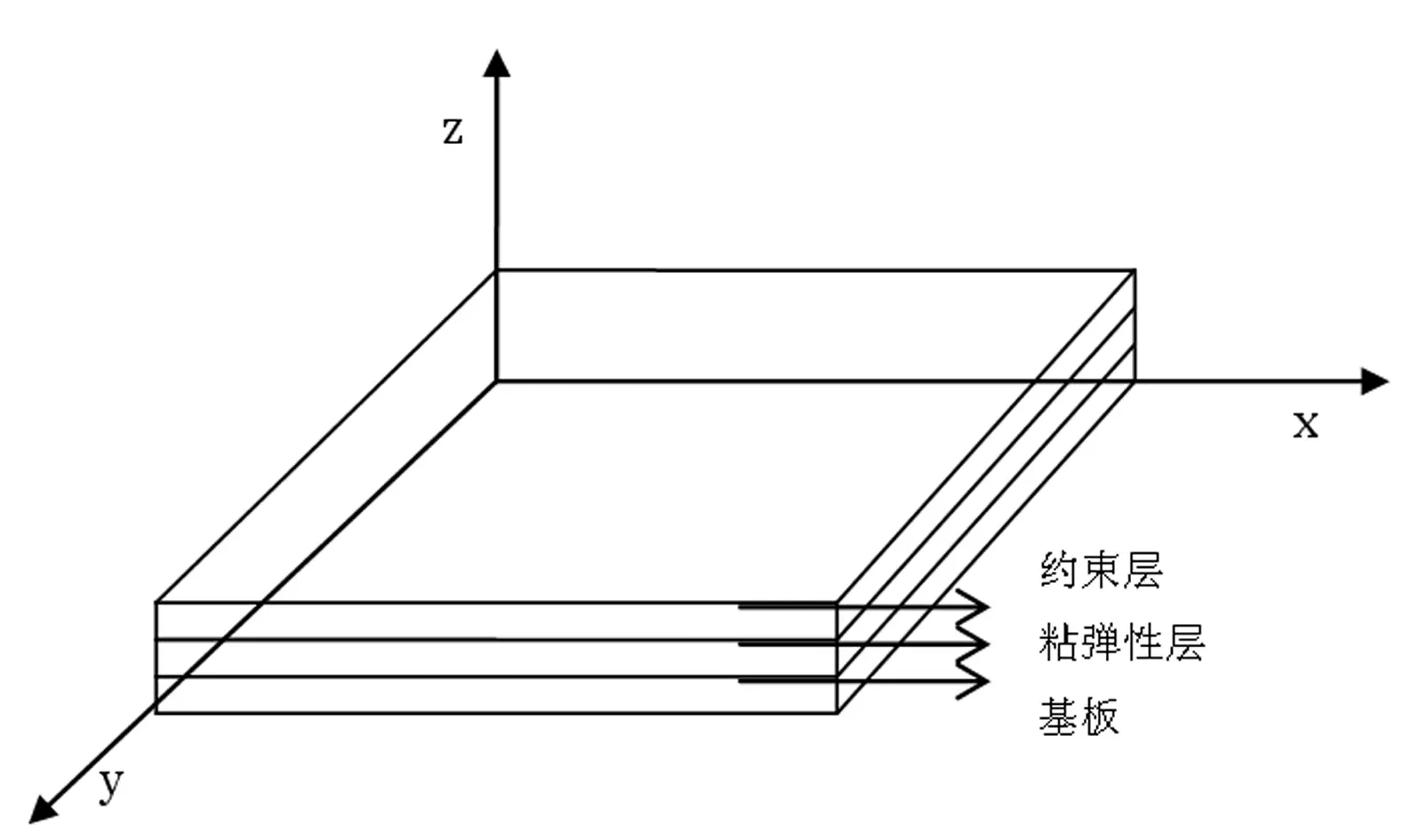
图1 约束层阻尼板单元

约束阻尼单元模型如图1所示。每个单元均由基板层、粘弹性(VEM)层和约束层组成，下标分别用p、v、c表示。每个节点有7个自由度，分别为约束层中性面内x方向的位移uci、约束层中性面内y方向的位移vci、基板层中性面内x方向的位移upi、基板层中性面内y方向的位移vpi、单元中性面的横向位移wi以及绕x轴方向的转角θxi和y轴方向的转角θyi。

节点位移向量为：

Δi={ucivciupivpiwiθxiθyi}T

(i=1,2,3,4)

(1)

单元位移向量为：

(2)

根据单元位移模式，可得约束层阻尼单元的形函数[13]：

N={[Nuc];[Nvc];[Nup];

[Nvp];[Nw];[Nwx];[Nwy]}

(3)

其中，Nuc、Nvc、Nup、Nvp、Nw、Nwx、Nwy分别为对应单元节点自由度uc、vc、up、vp、w、θx、θy的形函数。

约束阻尼单元各层的动能和应变势能如下[14]：

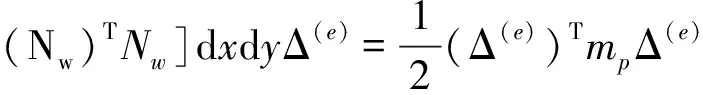
(4)

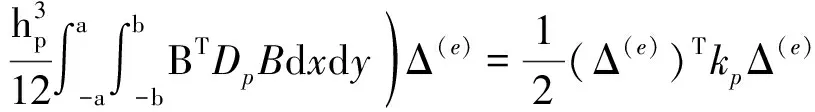
(5)

(Nvc)TNvc+(Nw)TNw]dxdyΔ(e)=

(6)

(7)

(Nvv)TNvv+(Nw)TNw]dxdyΔ(e)=

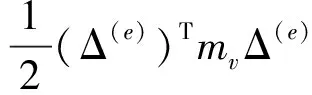
(8)

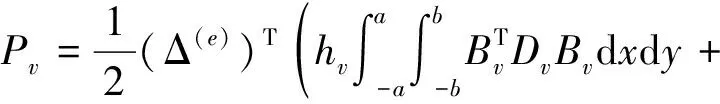
(9)

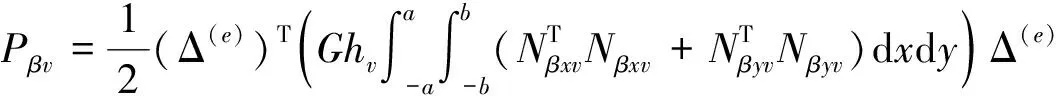
(10)

其中，T和P分别表示结构单元的动能和应变势能。运用Hamilton原理，可导出约束层阻尼单元的质量矩阵和刚度矩阵：

m=mp+mc+mv

(11)

k=kp+kc+kv+kβv

(12)

其中，mp、mc、mv分别为基板、约束层以及粘弹性层的质量矩阵，kp、kc、kv、kβv分别为基板、约束层、粘弹性层位移及横向剪切变形的刚度矩阵。将单元质量矩阵和刚度矩阵进行组集，获得约束层阻尼板结构的总体质量矩阵和刚度矩阵：

(13)

(14)

因此，约束层阻尼板的有限元动力学模型为：

(15)

这里，粘弹性层的剪切模量为G=Gv(1+ηi)，η为损耗因子，[K]为复刚度矩阵。

1.2 约束层阻尼板的振动模型

假设约束层阻尼板的外激励为简谐激励f(t)=Fejωt，位移响应满足x(t)=Xejωt。将以上两式代入(15)式，消去ejωt，得：

(-ω2[M]+[K]){X}={F}

(16)

因此，约束层阻尼板节点位移响应为：

{X}=[H(ω)]{F}

(17)

节点速度响应为：

{V}=iω{X}=iω[H(ω)]{F}

(18)

其中：H(ω)=(-ω2[M]+[K])-1为位移传递函数。

1.3 约束层阻尼板声辐射计算

将约束层阻尼板镶嵌于无限大刚性障板上，运用简化后的Helmholtz公式，即Rayleigh积分计算其声辐射。振动辐射声功率可由表面声压p(P)和表面法向速度vn(P)表示：

(19)

(20)

将(20)式代入(19)式：

(21)

考虑到格林函数的对称性，式(21)可表示为：

(22)

将式(22)写成矩阵形式，其中{V}为各单元上法向速度构成的向量。

W(ω)={V}T[R]{V}

(23)

在结构均匀离散情况下，矩阵R的形式为[15]：

(24)

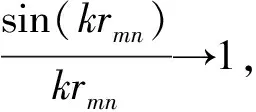
在一个频带内的平均声功率表示为：

(25)

离散后得：

(26)

其中，Wave表示频带内的平均辐射声功率，N表示频带内激励力频率的总数，ωi表示第i个激励力频率。

2 优化模型

以简谐激励作用下约束阻尼板辐射的声功率最小化为目标函数，约束阻尼材料体积分数为约束条件，建立拓扑优化模型：

(27)

其中，X={β1β2…βn}T为设计变量，表示约束阻尼单元的存在状态。当βi=1时，表明第i个单元位置有约束阻尼单元，当βi=0时，表明第i个单元位置无约束阻尼单元，n为约束阻尼单元总数，W为约束阻尼板辐射声功率，V为约束阻尼材料体积，V*是体积约束。

3 灵敏度分析

约束阻尼板的速度响应为：

V=iωX

(28)

速度对设计变量β的偏导数为：

(29)

将式(15)两端对设计变量h求偏导数：

(30)

将上式整理并代入式(29)，可得速度对设计变量的灵敏度[16]：

(31)

结合式(23)，可求出约束阻尼板辐射声功率对设计变量的灵敏度：

(32)

这里的设计变量β是约束阻尼单元的存在状态，根据式(31)，结合设计变量的定义，速度对设计变量的灵敏度可用约束阻尼单元删除前后的速度变化量来表示。同样，根据式(32)，声功率对设计变量的灵敏度也可以用约束单元删除前后的声功率变化值来表示。因此，速度对设计变量的灵敏度改写为：

ΔV=-iω(K-ω2M)-1(ΔK-ω2ΔM)X

(33)

声功率对设计变量的灵敏度改写为：

ΔW=ΔVHRV+VHRΔV

(34)

4 独立网格滤波

在连续结构拓扑优化过程中，常出现棋盘格式和网格依赖性等数值不稳定现象。采用独立网格滤波技术，以有效抑制棋盘格式和网格依赖性。独立网格滤波技术属于灵敏度过滤法，是一种局部意义上的约束方法，它以过滤半径范围内单元的灵敏度的加权平均值代替原来的灵敏度值。独立网格滤波方程为:

(35)

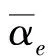
采用独立网格滤波技术，最重要的是选择合适的滤波半径，对阻尼单元的灵敏度信息进行滤波操作，它不仅能抑制棋盘格式，而且能消除网格依赖性。

5 优化流程

本文采用渐进优化算法，求解优化模型。渐进优化算法的基本思想是通过逐步删除设计域中的无效或低效单元，搜寻最佳的材料布局，使目标函数最小化或最大化。基于约束阻尼板辐射声功率的拓扑优化模型，可设计使约束层阻尼板辐射声功率最小化的拓扑优化计算流程，见图2所示。

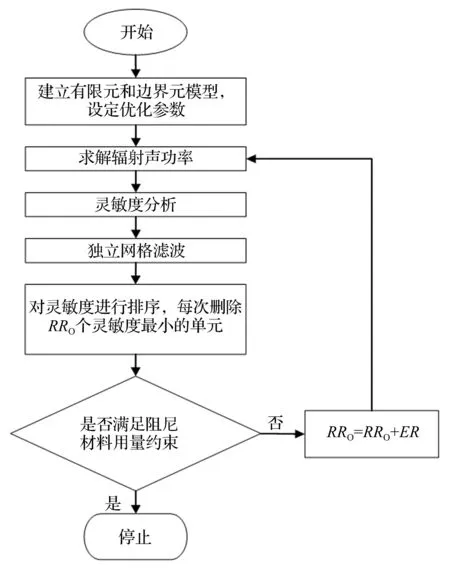
图2 约束阻尼板声功率优化设计流程图

优化步骤如下：

① 建立约束阻尼板的有限元模型和边界元模型；

② 给定约束阻尼材料的体积约束量以及初始删除量RR0和其进化量ER；

③ 对激励力作用下的结构进行声辐射分析，获得辐射声功率；

④ 按式(34)计算各阻尼单元的声功率灵敏度；

⑤ 设定适当的滤波半径，采用独立网格滤波技术对各单元的声功率灵敏度进行滤波；

⑥ 对滤波后的单元声功率灵敏度进行排序；

⑦ 删除RR0个单元的声功率灵敏度值最小的单元；

⑧ 判定是否达到约束条件。如果不满足约束条件，更新RR0=RR0+ER，并重复步骤③-⑧；如果满足约束条件，则结束迭代，输出结果。

6 算例分析

将四边简支的约束阻尼板镶嵌于无限大刚性障板上，计算约束层阻尼板的振动声辐射。约束层阻尼板的参数如下：

约束阻尼板长L=0.4 m，宽B=0.3 m。基层：Ep=7.0e10 Pa，ρp=2 800 kg/m3，μp=0.3，hp=0.000 8 m；粘弹性层：Ev=1.2e7 Pa，ρv=1 200 kg/m3，μv=0.495，hv=0.000 05 m，η=0.5；约束层：Ec=7.0e10 Pa，ρc=2 700 kg/m3，μc=0.3，hc=0.000 13 m。有限元网格单元数16×12，边界元网格单元数16×12，在(0.20,0.15,0)处即中心点受到正弦激励力：F=sinωt=sin(2πft)。空气密度ρ0=1.225 kg/m3，空气中声速c0=343 m/s。

6.1 一阶峰值声功率的拓扑优化

随着阻尼材料的删除，约束层阻尼板结构的声功率曲线会发生频移，因此，针对约束层阻尼板一阶峰值声功率的拓扑优化，必须在每次删除单元后，计算辐射声功率时，重新计算固有频率，进行频率跟踪。

优化过程中，每次删除4个单元，滤波半径取为4.5，将192个单元全部删除须进行48次迭代。图3是辐射声功率随删除率变化的迭代过程图。

图3 声功率随阻尼材料删除率的变化图

由图3可知，在阻尼材料删除过程中，约束阻尼板的辐射声功率有一定程度波动，因为在删除过程中被删除的单元灵敏度可能为正也可能为负，从而导致删除后约束阻尼结构的辐射声功率有波动。其中，约束层阻尼板的声功率有几个低点，当删除率为12.5%和35.4%时，辐射声功率均为112.1 dB，删除率为62.5%时，辐射声功率为112.2 dB，删除率为81.2%时，辐射声功率为113.3 dB。选取删除率为35.4%、62.5%和81.2%，分析一阶峰值声功率，并计算最优的拓扑构型图。

约束阻尼最优拓扑构型如图4～图6，黑色表示约束阻尼材料，白色为无约束阻尼材料，从动力学特性的角度来分析，粘贴约束阻尼材料的区域均是一阶模态应变能较大的区域，表明这些单元均是有效单元。基板、全覆盖板及不同阻尼材料用量下的辐射声功率对比见图7～图8所示，可以看出，随着约束阻尼材料用量的增加，声功率曲线向后发生频移，此外，在第一阶峰值处，35.4%、62.5%和81.2%删除率时，其辐射声功率均比基板和全覆盖板有所下降，由于拓扑优化保留了有效阻尼单元，删除了无效阻尼单元，在阻尼材料用量减小的情况下，获得了比全覆盖更低的辐射声功率。

图4 35.4%删除率下阻尼材料的最优拓扑图

图7 一阶峰值优化的辐射声功率对比图

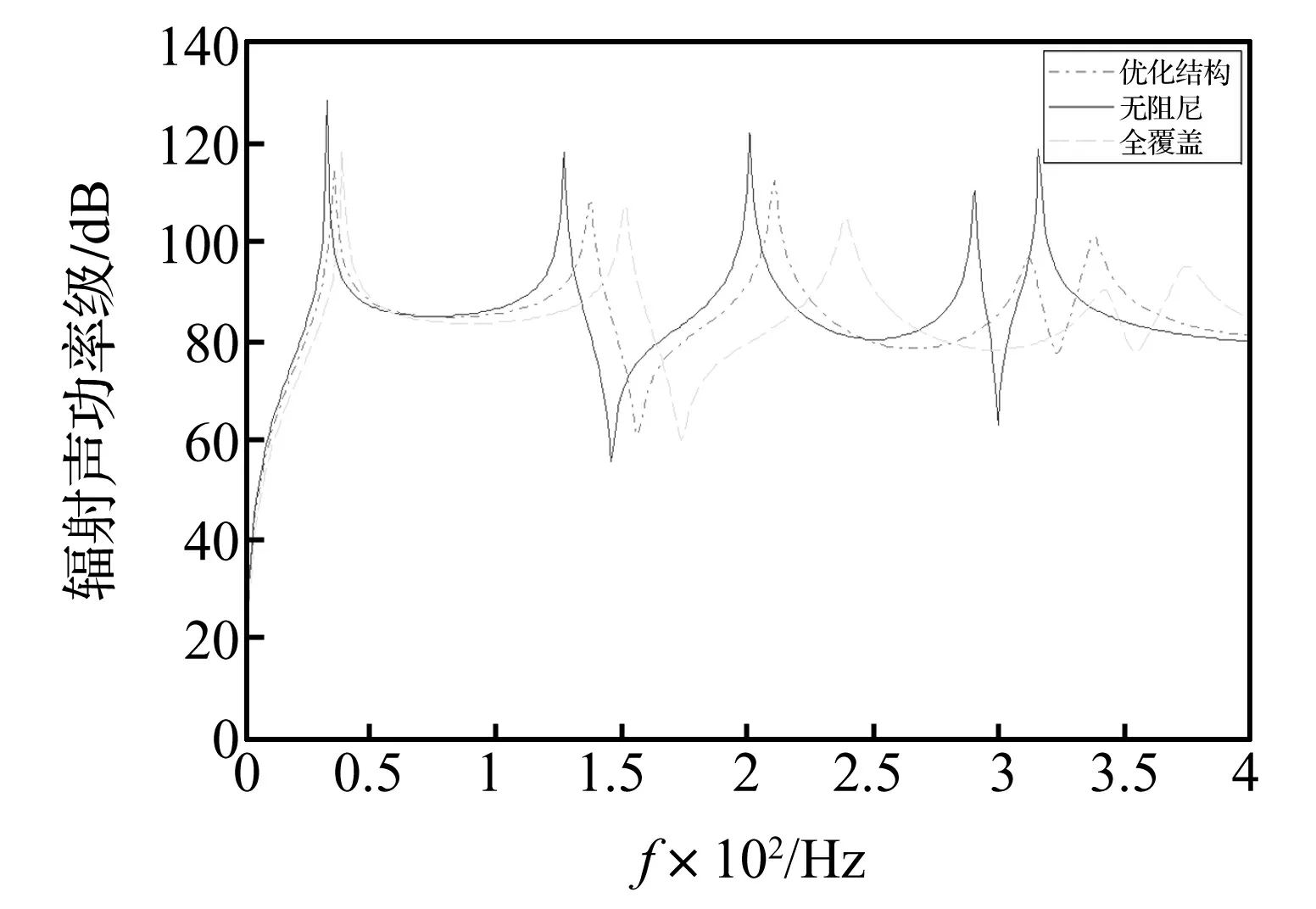
图10 频带优化的辐射声功率对比图

图11 频段内辐射声功率对比图

6.2 频带辐射声功率的拓扑优化

选取频率区间10 Hz-60 Hz，这是基板第一阶峰值所在的频率范围。阻尼材料删除率取为50%，步长为1 Hz，每次删除4个单元，滤波半径取为4.5。图9是约束阻尼材料最优拓扑构型，图10是基板、全覆盖以及最优拓扑构型下的声功率对比图。

图11表明，优化后的约束阻尼板，其辐射平均声功率比基板和全覆盖板更低；在目标频率区间，优化结构的平均声功率为99.7 dB，基板为111.4 dB，全覆盖为102.1 dB，优化后的约束阻尼板，其平均声功率分别下降11.7 dB和2.4 dB。

7 结 论

本文建立了约束层阻尼板的有限元模型，用Rayleigh积分推导了约束层阻尼板的辐射声功率及其灵敏度表达式，以辐射声功率最小化为目标，采用渐进优化算法对约束阻尼材料布局进行了拓扑优化。研究结果表明：本文提出的理论模型和拓扑优化算法是正确和有效的，无论是针对一阶峰值或是某一频带，它均能以较少的约束阻尼材料，实现结构振动声辐射最小化的目标。约束层阻尼板振动声辐射的优化为结构低噪声设计提供了重要的理论参考和技术手段。

参 考 文 献

[1]Bendsoe M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[2]Luo J, Gea H C. Optimal stiffener design for interior sound reduction using a topology optimization based approach[J], Journal of Vibration and Acoustics, 2003, 125:267-273.

[3]Akl W, Baz A. Topology optimization of a plate coupled with acoustic cavity[J]. International Journal of Solids and Structures, 2009, 46: 2060-2074.

[4]郭中泽,陈裕泽,侯 强,等. 阻尼材料布局优化研究[J]. 兵工学报, 2007, 28(5): 638-640.

GUO Zhong-ze, CHEN Yu-ze, HOU Qiang, et al. Damping material optimal placement in damping structure design[J]. Acta Armamentarii, 2007, 28(5): 638-640.

[5]杨德庆,柳拥军,金咸定. 薄板减振降噪的拓扑优化设计方法[J]. 船舶力学, 2003, 7(5): 91-96.

YANG De-qing, LIU Yong-jun, JIN Xian-ding, et al. Structural topology optimal design to reduce vibration and noise of thin plate[J]. Journal of Ship Mechanics, 2003, 7(5): 91-96.

[6]李以农,谢熔炉,王 宜,等. 约束阻尼结构拓扑优化设计的进化算法[J]. 重庆大学学报, 2006, 10(2): 120-125.

LI Yi-nong, XIE Rong-lu, WANG Yi, et al. Topology optimization for constrained layer damping material in structures using ESO method[J]. Journal of Chongqing University(Natural Science Edition), 2006, 10(2): 120-125.

[7]郑 玲,谢熔炉,王 宜,等. 基于优化准则的约束阻尼材料优化配置[J]. 振动与冲击, 2010, 29(11): 156-179.

ZHENG Ling, XIE Rong-lu, WANG Yi, et al. Optimal placement of constrained damping material in structures based on optimality criteria[J]. Journal of Vibration and Shock, 2010, 29(11): 156-179.

[8]李 超,李以农,施 磊,等. 圆柱壳体阻尼材料布局拓扑优化研究[J]. 振动与冲击, 2012, 31(4): 48-52.

LI Chao, LI Yi-nong, SHI Lei, et al. Topological optimization for placement of damping material on cylindrical shells[J]. Journal of Vibration and Shock, 2012, 31(4): 48-52.

[9]王明旭,陈国平. 基于变密度方法约束阻尼层动力学性能优化[J]. 南京航空航天大学学报, 2010, 42(3): 283-287.

WANG Ming-xu, CHEN Guo-ping. Dynamics performance optimization of constrained damping layer using variable density method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3): 283-287.

[10]吕毅宁,吕振华,赵 波,等. 附加自由阻尼结构系统的有限元分析和拓扑优化设计方法研究[J]. 计算力学学报, 2012, 29(2).

LÜ Yi-ning, LÜ Zhen-hua, ZHAO Bo, et al. A finite element analysis and topology optimization method for structures with free damping[J]. Chinese Journal of Computational Mechanics, 2012, 29(2).

[11]Duhring M B, Sigmund O. Acoustic design by topology optimization[J]. Journal of Sound and Vibration, 2008, 317: 557-575.

[12]Denli H, Sun J Q. Structural-acoustic optimization of sandwich structures with cellular cores for minimum sound radiation[J]. Journal of Sound and Vibration, 2007, 301: 93-105.

[13]刘天雄,华宏星,陈兆能,等. 约束层阻尼板的有限元建模研究[J]. 机械工程学报, 2002, 38(4): 108-114.

LIU Tian-xiong, HUA Hong-xing, CHEN Zhao-neng, et al. Study on the model of finite element of constrained layer damping plate[J]. Chinese Journal of Mechanical Engineering, 2002, 38(4): 108-114.

[14]龚培康. 汽车拖拉机有限元法基础[M]. 北京:机械工业出版社, 1995.

[15]刘宝山,赵国忠,顾元宪. 复合材料层合板结构振动声辐射优化[J]. 振动与冲击, 2008, 27(12): 31-35.

LIU Bao-shan, ZHAO Guo-zhong, GU Yuan-xian, et al. Optimization of acoustic radiation caused by structural vibration of composite laminated plates[J]. Journal of Vibration and Shock, 2008, 27(12): 31-35.

[16]袁国清. 基于声辐射模态模型求解声学灵敏度[D]. 镇江:江苏大学, 2009.