基于无单元声波叠加的自辐射近似解析表达研究
吴绍维, 向 阳, 夏雪宝
(1.武汉理工大学 能源与动力工程学院,武汉 430063;2.船舶动力系统运用技术交通行业重点实验室,武汉 430063)
随着有限元法近十几年来的巨大发展,有限元法已成为工程数值分析的有效工具,解决了很多有重大意义的科学和工程问题。但是,有限元法在分析高速冲撞、动态裂纹扩展和应变局部变化等问题时遇到了因网格畸变产生的许多困难[1],自上世纪90年代结构力学领域逐步发展了无单元计算方法[2],这种无单元方法起源于裂纹扩展问题[3]。裂纹扩展问题的计算要求很密集的网格单元,并且在分析计算中还要求网格自适应,这增加了计算负担。在无单元计算方法中去除了网格只考虑计算模型中的节点,每个节点给予一定的用于计算的区域,这样很大程度上减轻了计算负担。Koopmann[4]提出了传统的波叠加法,即任何振动辐射体表面辐射的声场可通过该辐射体内部虚拟构建的简单球型源产生的声场叠加进行求解,利用实际辐射体表面法向速度边界条件确定虚拟声源的强度。这些虚拟构建的声源满足波动方程,并且这种方法被证明等效于Helmholtz积分方程。这种方法对结构简单的模型很实用,与边界元法相比具有计算速度快,精确性高,当虚拟声源位于辐射体内时无奇异的特点。但是虚拟声源必须位于实际辐射体内的一定范围内才能用于声场计算。对于脉动球源模型,虚拟球型声源半径与实际球源半径之比须在0.05—0.4[4]范围以内才能较为准确的计算出表面声压;对结构复杂的模型,虚拟等效源的位置和所在的几何形状对声场计算的精确性具有很大的影响,目前还处于进一步研究当中[5-7]。受到无单元计算方法的启示,Koopmann 的学生Brian Zellers将无单元计算方法用到计算结构振动声辐射的问题中,将无单元计算方法与波叠加法相结合使得声场的计算大为简化,对求解任意振动结构辐射的声场只需矩阵运算[8-10],不需要构建位于实际辐射体内部的虚拟声源。但在Brian Zellers的研究中未能推导出偶极子自辐射项的解析表达,他采用文献[11]中无障板活塞辐射阻抗的表达式来代表偶极子自辐射速度项,这种表达方式无法直接计算,需通过多个方程的复杂求解过程来获取计算所需要的参数。针对所存在的问题,本文对无单元空间离散域的声波叠加法进行了进一步的研究,分别通过奇异点挖去法推导单极子自辐射声压项近似解析表达,积分区域替换法推导单极子自辐射速度项和偶极子自辐射声压项的近似解析表达,不变量嵌入法推导偶极子自辐射速度项近似解析表达。最后用脉动球源作为实例,验证了单、偶极子点声源自辐射项的精确性。
1 无单元空间离散域的声波叠加法
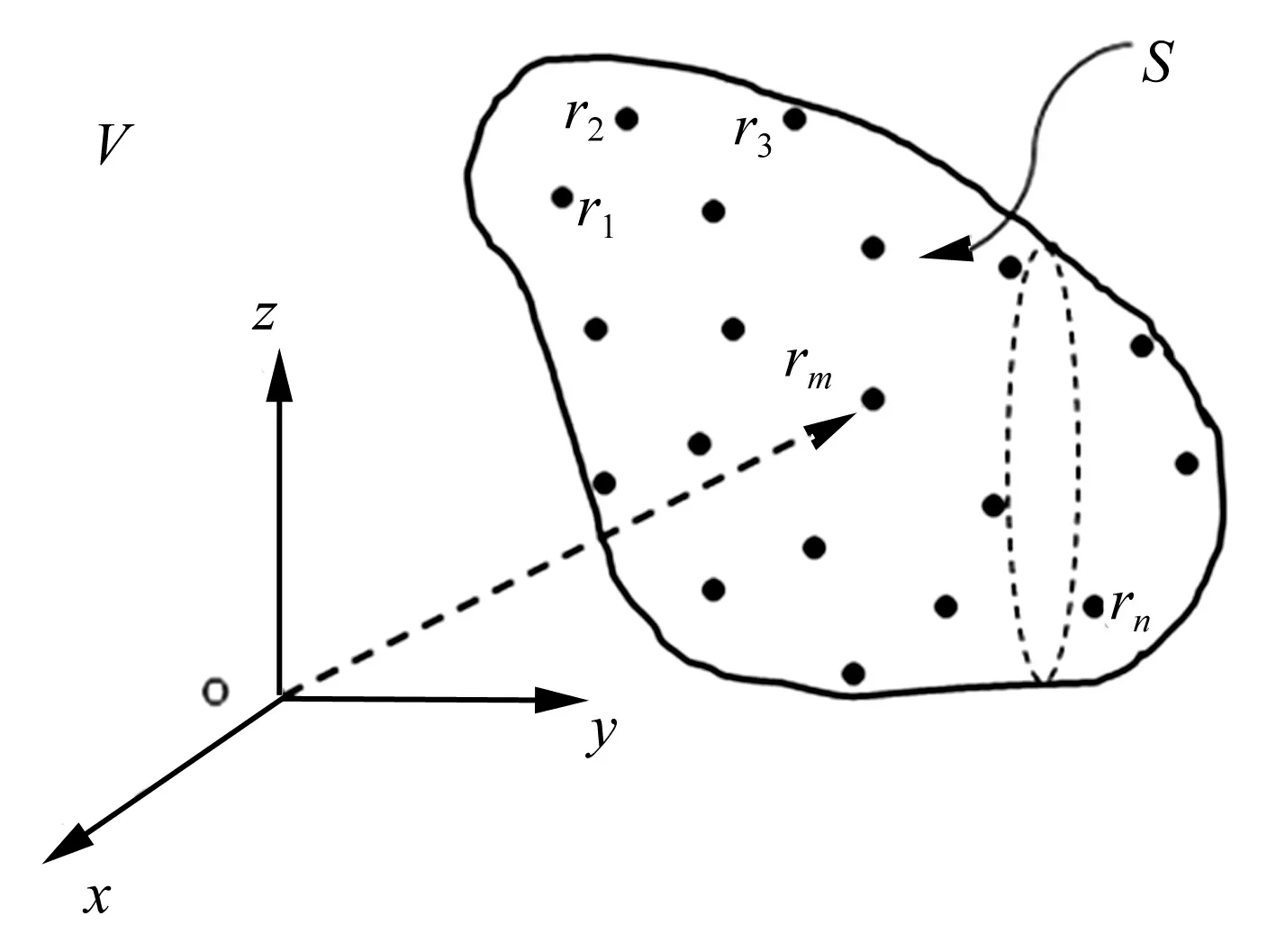
图1 波叠加法示意图
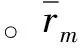
(1)
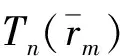
(2)
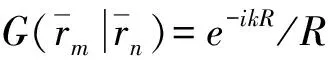
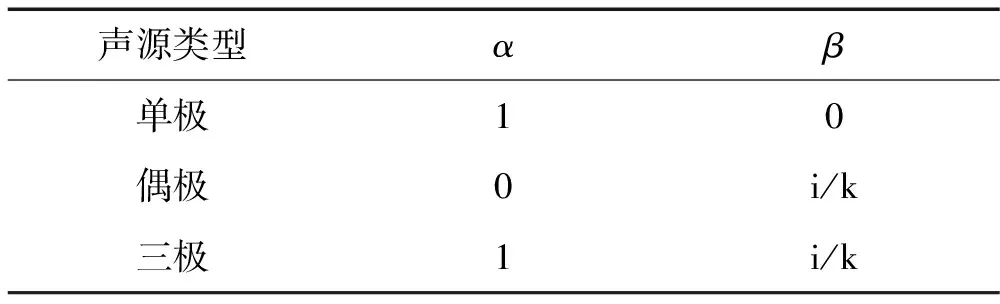
表1 α,β值及其组合
本文使用体积速度边界条件来确定声源强度sn[12]。体积速度定义为振动结构的表面法向速度在振动表面面积区域上的积分。为保证计算的精确性,这里将振动辐射表面划分成N个区域,区域上的体积速度为法向速度在域上的积分。由欧拉方程可知声场中任意一质点速度与声压的关系为:
(3)
这里ρ为声介质密度(1.21 kg/m2),其中m是对接收点求梯度。这里速度为方程(3)可以写成
(4)


(5)
定义Umn为
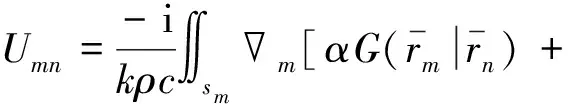
(6)
用矩阵形式表示方程(6)为
(7)
通过体积速度条件解出声源强度[sn],并代回到方程(1)即可确定辐射体表面声压。已知声压和速度,将平均声强在一个远场处包围辐射体的S面上积分,可求得平均声功率,其中式(8)中的上标H表示复共轭转置,即Hermitian转置
(8)
通过上述分析可知:用无单元空间离散域波叠加法进行声场计算,只需在实际辐射体表面选取离散的点,而不需要在辐射体内部构建虚拟声源。
2 格林函数奇异性及自辐射项的近似解析表达
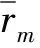
采用无单元法进行声场波叠加计算时先将振动结构表面离散化,离散化的区域几何中心称之为节点,将点声源置于这些节点处。本文在推导自辐射项的近似解析表达式时,取以节点为圆心,a0为半径的圆形作为积分区域,圆形的面积等于离散化时节点所在的区域面积,如图2所示。将位于节点处的点声源对自身所在的圆形区域所辐射的声压及由辐射导致的速度在圆形区域上积分并取平均,平均声压和平均速度可用于表达单、偶极子自辐射的声压项和速度项,在本文中对单极子点声源和偶极子点声源的自辐射项进行了研究,接下来将给出详细的推导过程。

图2 点声源对小单元的辐射
2.1 单极子自辐射声压项近似解析表达式
为了解决单极子模型中格林函数的弱奇异性,去掉以节点为圆心,半径为δa0的圆形部分,如图3所示。将位于节点处的单极子声源对环形区域所辐射的声压及由辐射导致的速度在环形区域上积分并取平均,这些值将随着δa0变化,当δa0趋近于0,平均声压和平均速度可用于表达单极子自辐射的声压项和速度项。

图3 单极子对环形小单元的辐射
根据声学理论和波叠加法原理,单极子辐射的声压可表达为第一类自由空间格林函数与声源强度的乘积,即
(9)
这里sm为单极子声源强度,r为单极子点声源与环形区域上点之间的的距离。单极子对环形区域辐射的平均声压定义为
(10)
这里a0为图3所示积分区域半径,δa0为去掉的那一部分的半径。令
(11)
对式(11)积分得:
(12)
当δa0→0时,对gm取极限得到单极子自辐射声压项近似表达式如下:
(13)
2.2 单极子自辐射速度项近似解析表达式
根据方程(3),圆形区域上接收点处的速度v与声压p之间的关系为
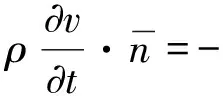
(14)
vm=sm
为克服被积函数的奇异性,将积分区域分为两部分,一部分替换为半径为r的半球面域s1,另一部分为s0-s1的环形平面域,如图4所示,其中r为单极子声源与s1上的点之间的距离,R为单极子声源与s0-s1上的点之间的距离。则:
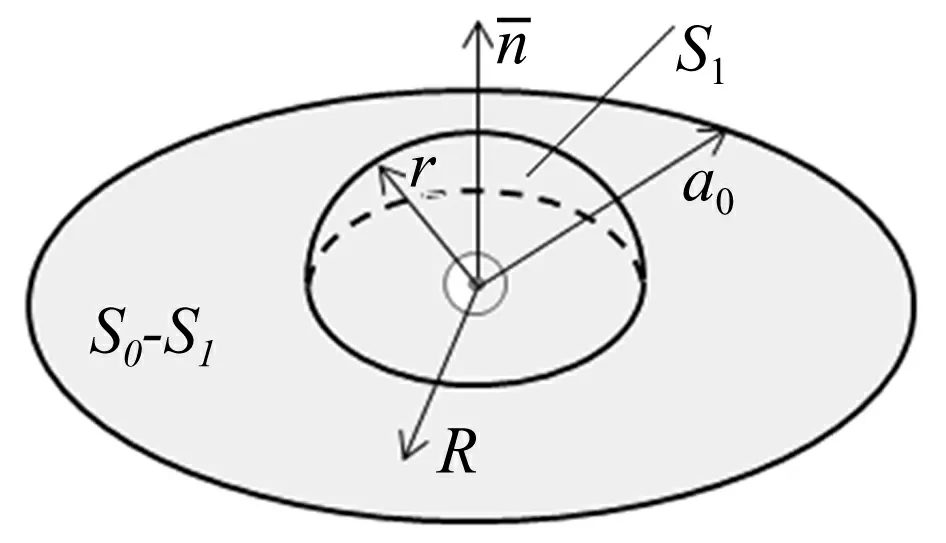
图4 单极子自辐射速度项积分域示意图
vm=sm
(16)
因为在s0-s1上mR垂直于故采用球坐标积分则
(17)
当r→0时,对取极限得单极子极子自辐射速度项的近似解析表达式,即:
(18)
2.3 偶极子自辐射声压项近似解析表达式
(19)
偶极子对圆形区域辐射的平均声压定义为:
(20)
其中a0为圆形区域的半径,s0表示圆形积分区域。为克服被积函数的奇异性,将积分区域分为两部分,一部分替换为半径为r的半球面域s1,另一部分为s0-s1的环形平面域,如图5所示。

图5 偶极子自辐射声压项积分域示意图
则:

(21)
其中r为偶极子声源与s1上的点的距离,R为偶极子声源与s0-s1上的点的距离。在环形平面域s0-s1上,dR垂直于故则
(22)
在s1上采用球坐标进行积分,则

(23)
当r→0时,对gd取极限得偶极子自辐射声压项的近似解析表达式,即:
(24)
2.4 偶极子自辐射速度项近似解析表达式
根据方程(3),圆形区域上接收点处的速度v与声压p的关系为
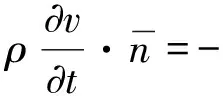
(25)
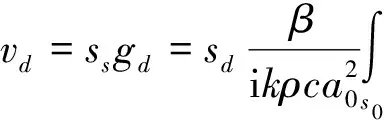
(26)
为克服被积函数中格林函数的超奇异性,对(26)中的被积函数进行恒等变形

(27)
(28)
令
(29)
(30)
则G=G1+G2。将G1展开为泰勒级数
(31)
将式(30),式(31)代入式(28)得到:
(32)

(33)
令
(34)
(35)
(36)
很容易求得
I2=πa0k2
(37)
(38)
对于I1这样的超奇异积分,采用Invariant Imbedding Method[13]求取有限积分值。定义积分函数
(39)
其中R为n维空间中,点到坐标原点的距离。需要计算的积分为
(40)
并定义β=lj1+lj2+…+ljn-h为被积函数f的度,α=β+n为该奇异积分I的度。则对于α≠0的奇异积分的积分有限值为
(41)
对于I1,β=-3,α=-1则
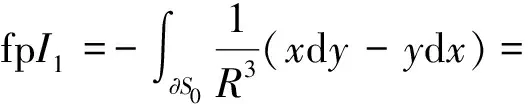
(42)
∂S0是圆形区域的边界。用fpI1替代I1,将式(37),式(38),式(42)代入式(33),从而偶极子自辐射速度项的近似解析表达式为:
(43)
3 自辐射近似表达的实例验证
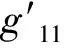
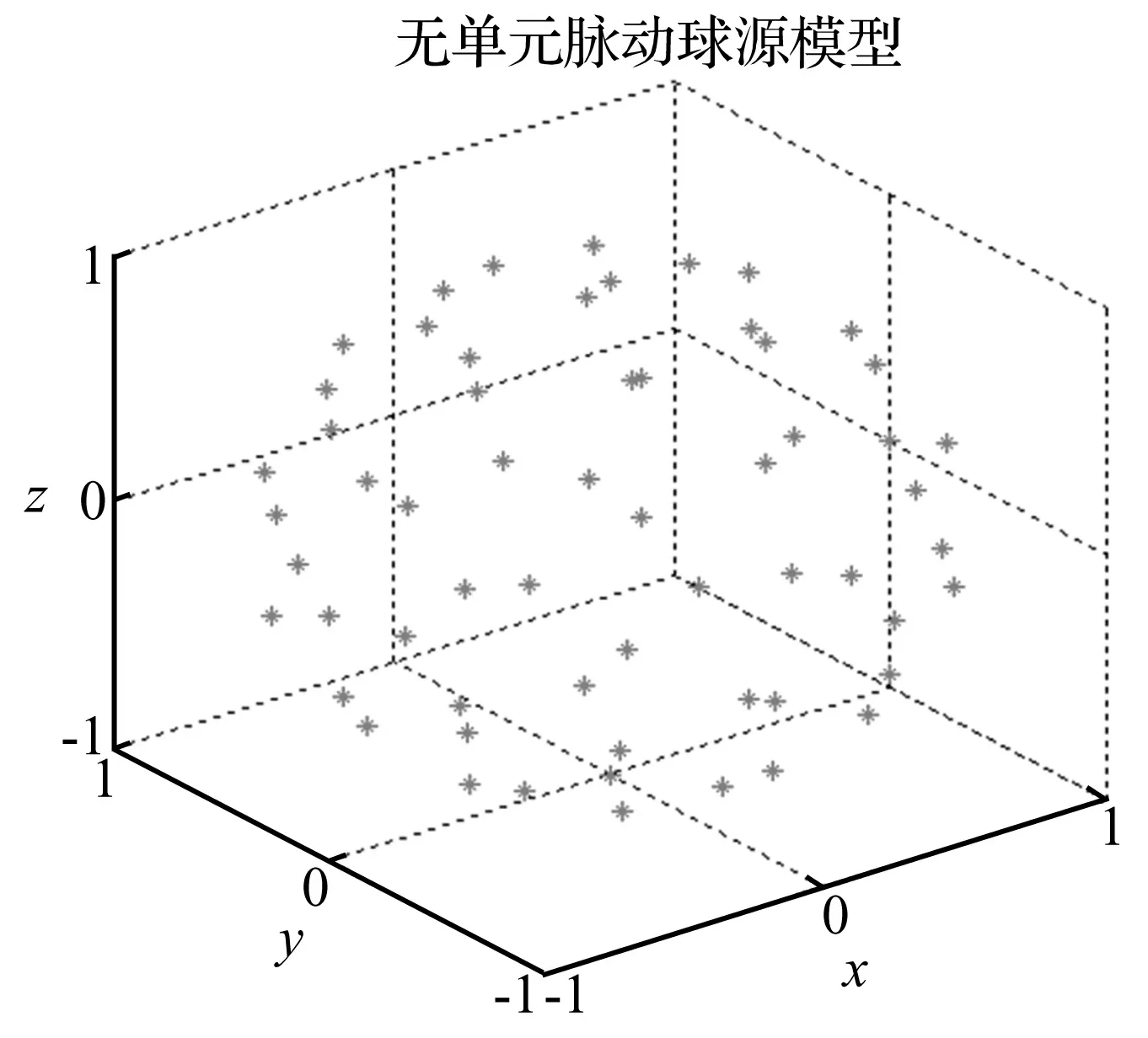
图6 无单元脉动球源模型
脉动球源所辐射的声压解析解为[14]
(44)
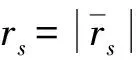
(45)
当rs>a时没有奇异性问题发生,考虑到脉动球源在整个表面均匀的辐射,每个点声源强度均相等,用ss表示,可求得ss如下:
(46)
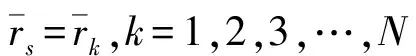
(47)
这里g11代表自辐射声压项,其中ps为式(44)中当rs=a时所确定的球面上的声压。解方程(47)得:
(48)
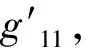
(49)
由方程(4)很容易得到
(50)


图7 20个节点模型单极子自辐射声压项近似解析表达式与数值解对比
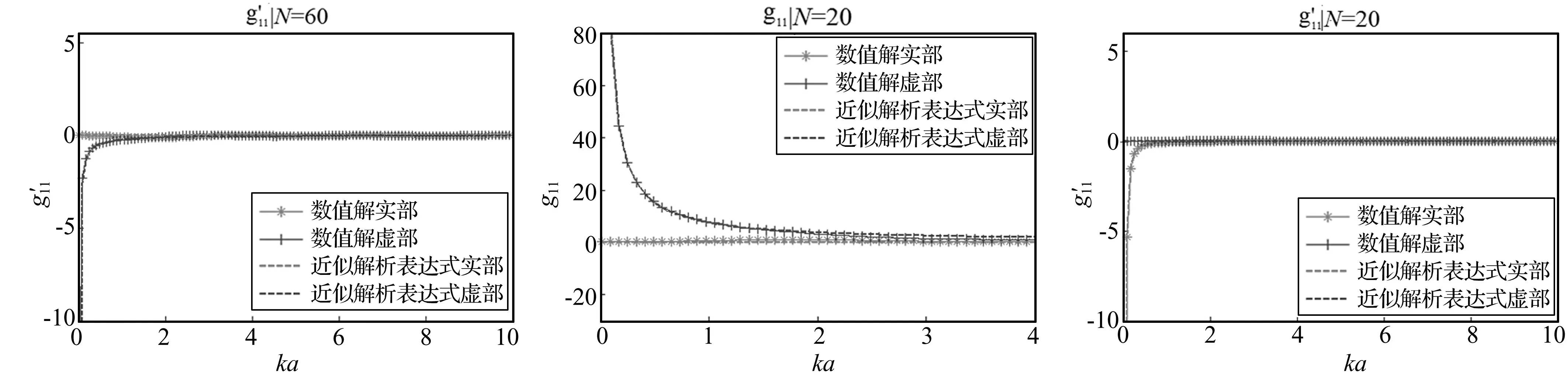
图10 60个节点模型单极子自辐射速度项近似解析表达式与数值解对比

图13 60个节点模型偶极子自辐射声压项近似解析表达式与数值解对比

图14 60个节点模型偶极子自辐射速度项近似解析表达式与数值解对比
由以上结果对比中可以看出,20个节点单、偶极子模型自辐射声压项与速度项近似解析表达式与数值解在ka=0~4内具有较好的一致性,声压项近似解析表达式在接近ka=4时有轻微的偏离,这是因为当频率增加时,声波波长变小,用于计算的圆形区域尺寸已经不满足所规定的条件(要求圆形区域的尺寸须小于λ/6,这类比于有限元计算中求解频率越高,网格必须划分的越细,以满足小单元尺寸与声波波长的关系)。对于60个节点,单、偶极子模型近似解析表达式与数值解也具有较好的一致性,当ka≥7时,自辐射声压项近似解析表达式与数值解的偏离相比ka取较小值时增大,这也是因为随着k值增加,波长减小,用于积分的圆形区域尺寸不满足所规定的条件所致。
4 结 论
本文针对无单元声波叠加自辐射项存在的弱奇异、奇异和超奇异问题,利用部分积分区域替换等方法推导了单、偶极子的自辐射声压项和速度项,通过实例验证表明所求得的自辐射项近似解析表达式在中低频时能够较为准确的表达自辐射项,可用于声场的计算,即克服了奇异性问题。但在中高频时,自辐射项与数值解存在一定程度的偏离。在较高频率处,是因为波长变小用于积分的圆形区域尺寸不满足条件所致,直接的方法是取更多的声源点,但是增加声源点数会导致相邻声源距离减小,其格林函数出现近奇异性的问题。因此解决这种矛盾还需要进一步研究,此问题解决后即可解决高频偏离问题。
参 考 文 献
[1]张雄, 刘岩. 无网格法[M]. 北京市:清华大学出版社,2004.
[2]Nayroles B, Touzot G,Villon P. Generalizing the finite element method: diffuse approximation and diffuse element[J]. Computational Mechanics, 1992, 10(5): 307-318.
[3]Belytschko T, Lu Y Y, Gu L. Element-free galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994,37(2):229-256.
[4]Koopmann G H, Songl,Fahnline J B, A method for computing acoustic fields based on the principle of wave superposition[J].Journal of Acoustic Society America,1989,86(6):2433-2438,
[5]李加庆,陈进,杨超,等. 基于波束形成和波叠加法的复合声全息技术[J]. 声学学报,2008,33(2):152-158.
LI Jia-qing, CHEN Jin, YANG Chao. A hybrid acoustic holography technique based on beamforming and ave superposition algorithm[J]. Acta Acustica, 2008, 33(2):152-158.
[6]熊济时,吴崇健,曾革委,等. 基于波叠加法的圆柱壳声辐射计算[J]. 舰船科学技术,2011,33(1): 54-58.
XIONG Ji-shi, WU Chong-jian, ZENG Ge-wei. Sound radiation numeration of cylinder based on the wave superpositionmethod[J]. Ship Science and Technology, 2011,33(1): 54-58.
[7]程鸿翔,尚德江,李琪,等. 声场匹配波叠加法的水下结构声辐射预报[J]. 声学学报,2013,38(2):137-146.
CHENG Hong-xiang, SHANG De-jiang, LI Qi. Sound radiation prediction for underwater structure by field-matching wave superposition method[J]. Acta Acustica, 2013,38(2):137-146.
[8]Zellers B. Element free structural acoustic for efficient shape optimization[C]. IMECE2005-82958.Orlando, Florida USA, 2005,125-135.
[9]Zellers B. An acoustic superposition method for computing structural radiation in spatially digitized domains[C].IMECE2007-41313.Seattle,Washington,USA,ASME,2007.
[10]Zellers B. An acoustic superposition method for computing structural radiation in spatially digitized domains[D]. Pennsylvania: Department of Mechanical and Nuclear Engineering, The Pennsylvania State University,2006.
[11]Mellow T, Karkkainen L. On the sound field of an oscillating disk in a finite open and closed circular baffle[J]. Journal of the Acoustical Society of America, 2005, 118(3), 1311-1325.
[12]Koopmann G H. Designing quiet structures[M]. 525 B Street, Suite 1900,San Diego, California 92101-4495,USA: Academic Press ,Inc 1997.
[13]Vijayakumar S. An invariant imbedding methoad for singular integral evaluation on finite domains[J]. SIAM Journal on Applied Mathematics, 1988,48(6): 1331-1349.
[14]杜功焕,朱哲民,龚秀芬. 声学基础[M]. 第三版.南京市:南京大学出版社,2012.

