斜齿行星传动多体动力学建模与分析

张 俊， 刘先增

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

行星齿轮传动的振动和噪声是影响系统可靠性、寿命及操作环境的关键因素。围绕该类传动的动力学问题，学术界开展了大量研究，内容涉及动力学建模、固有特性分析、动态响应求解、振动噪声抑制等多个方面[1]。这其中，动力学建模和分析是进行后续动力性能研究及减振降噪的理论基础。相比直齿行星传动，斜齿行星传动的结构、受力更为复杂，其动力学建模和分析也更具挑战性，故迄今为止针对斜齿行星传动动力特性的研究较少[2-4]。

按建模方法和考虑因素的不同，大致可将行星传动的动力学模型分为解析模型、有限元模型和多体模型三类。其中，解析模型因建模简单、求解容易等优点而被广泛采用。Kahraman[2]建立了斜齿行星传动的三维解析模型，并依托所建模型分析了行星轮啮合相位等参数对轮系动力特性的影响。该解析模型中，各构件均被视为具有6自由度的刚体，各刚体间的啮合和支承简化为具有集中效应的弹簧阻尼单元。延续这一思路，Lin和Parker等通过建立计入构件平移、扭转运动的解析模型获得了直齿行星传动固有特性的解析表达式，并将系统的自由振动归纳为扭转(rotational)、平移(translational)和行星轮(planet)三种模式[5]。采用类似解析模型，学者们进一步研究了参数灵敏度[6]、模态跃迁[7]、参数稳定性[8]、非均布行星轮系统[9]、复合行星轮系[10]及人字齿、锥齿行星轮系模态[11]等问题。

不同于解析模型将轮系视为具有集中效应的弹簧质量系，有限元模型可有效计入系统各环节的影响。Kahraman等运用有限元法建立了行星轮系的准静态受力模型，分析了内齿圈柔性对齿轮应力和行星轮载荷分配的影响[12]。采用类似手段，该文作者又进一步研究了内齿圈柔性对系统动态特性的影响[13]。文献[12-13]的研究表明，构件柔性有助于补偿因齿轮和系杆制造安装误差引起的非均载效应，且对系统动态特性具有重要影响。此外，文献[14-16]也采用类似的有限元模型对行星轮系的动态特性进行了研究，也得出了一些重要结论。

尽管有限元模型相较于解析模型具备更高的分析精度，但由于该类模型的建立和求解均较为费时，故不适用于需要反复迭代的初始设计阶段。相比之下，介于解析模型和有限元模型之间的多体动力学模型既能很好地反映行星轮系的质量集中特点，又能有效规避有限元模型的冗余繁杂，为行星轮系的动力学分析提供了新的解决方案。特别是随着近年来一些商用软件如Simpack、Virtual.lab、ADAMS、RecurDyn等的成功应用，采用多体动力模型对行星轮系进行动力学分析已成为行之有效的手段[17-19]。

有鉴于此，本文拟运用多体动力学方法，建立斜齿行星传动的多体动力学模型，进而依托所建模型对轮系进行自由振动分析，并将分析结果与前人提出的解析模型的结果作对比，以验证多体动力学模型的可靠性。在此基础上，进一步开展斜齿行星轮系的动态响应和参数影响分析，以期为后续的动态设计与性能优化提供理论依据。

1 多体动力学建模

为方便建模并不失一般性，作如下假设：

(1) 忽略各齿轮体、系杆和箱体的柔性，将其按刚体处理；

(2) 计入各齿轮副的啮合变形和各构件的支承变形，以具有等效刚度的线性时变/不变弹簧代替；

(3) 各齿轮副的啮合力始终作用在啮合平面内，并与理论接触线垂直；

(4) 各啮合轮齿间不存在脱齿和啮入/啮出冲击；

(5) 不考虑原动机和负载的惯性；

(6) 各行星轮的质量、惯量和平均啮合刚度均相同。

基于上述假设，建立如图1所示的多体动力学模型。

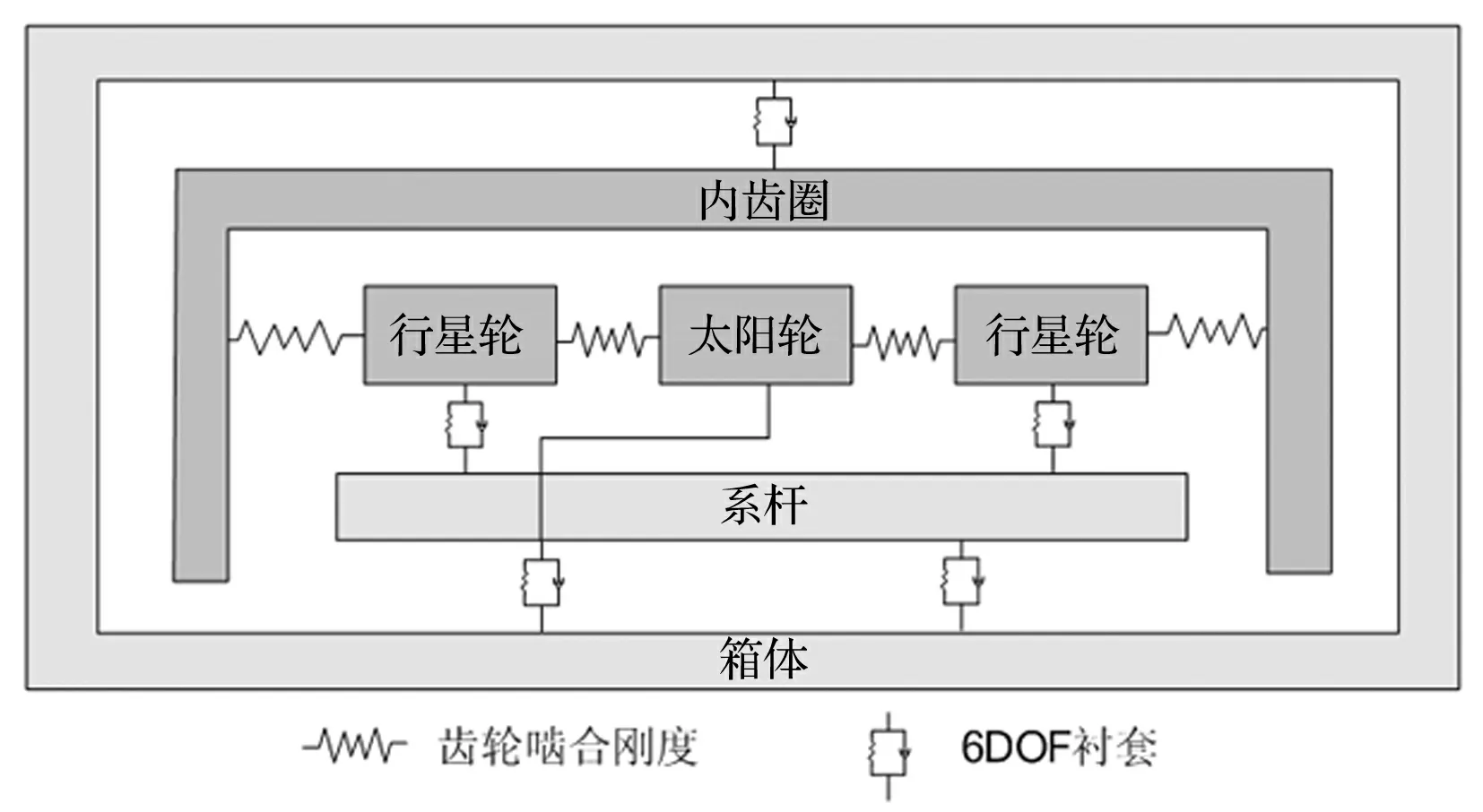
图1 斜齿行星传动多体动力学模型

图中，除箱体按固定件处理，其余构件均拥有6自由度。太阳轮和行星轮、行星轮和内齿圈之间以线性时变弹簧联接，弹簧刚度取为相应齿轮副的啮合刚度(详见GB/T 3480—1997斜齿轮平均啮合刚度的计算)。太阳轮、内齿圈及系杆与箱体之间、行星轮与系杆之间的联接均以6自由度衬套代替，衬套各方向数值的计算可参见文献[20]。篇幅所限，上述各刚度数值的计算不再详列。

图2为斜齿行星传动的机构示意图，为清晰计未示出系杆。定义全局坐标系O-XYZ，其中原点O取为轮系的几何中心，X轴取为水平向右，Y轴取为垂直向上，Z轴由右手定则确定。在该坐标系下，各构件的弹性位移以qi表示，且有qi=[xi,yi,zi,uxi,uyi,uzi]T(i=s,r,c,1,2,…,N)，下标s、r、c、n(n=1,2,…,N)分别表示太阳轮、内齿圈、系杆和第n个行星轮。各符号的含义可参见文献[3]。

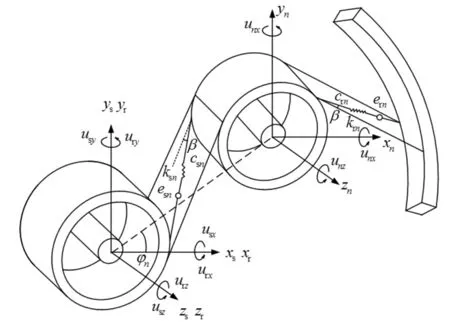
图2 斜齿行星传动啮合关系示意图

根据图2所示的几何关系，不难推导出内、外啮合副沿理论啮合线的相对位移δsn、δrn。

(1)

(2)

(3)

(4)

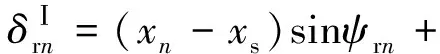
(5)

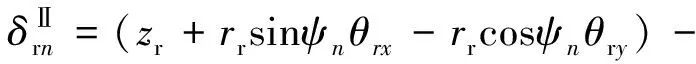
(6)

式中，ψsn=ψn-αs，ψrn=ψn+αr，ψn、αs、αr分别为第n个行星轮的位置角、外啮合副啮合角和内啮合副啮合角。

由多体动力学理论，系统的动能可写成如下形式

(7)

式中，mi为各构件在全局坐标系下的质量。该式可进一步写成如下矩阵形式

(8)

同样不难给出系统的势能表达式

(9)

上式同样可写成矩阵形式如下

(10)

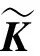
进一步运用拉格朗日方程，可推导出系统的运动微分方程如下

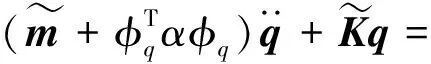
(11)

式中，φ为系统的总体约束矩阵，F为系统外载荷列阵，φq为各构件弹性变形的Jacobian矩阵，μ、Ω为介于1～10间的罚系数[21]。限于篇幅，略去上述各矩阵元素及标量的具体推导过程。

2 动态特性仿真

不失一般性，以表1所示的参数为例进行斜齿行星轮系的动态特性仿真。设系统的输入构件为太阳轮，输出构件为系杆，内齿圈与机壳制为一体。

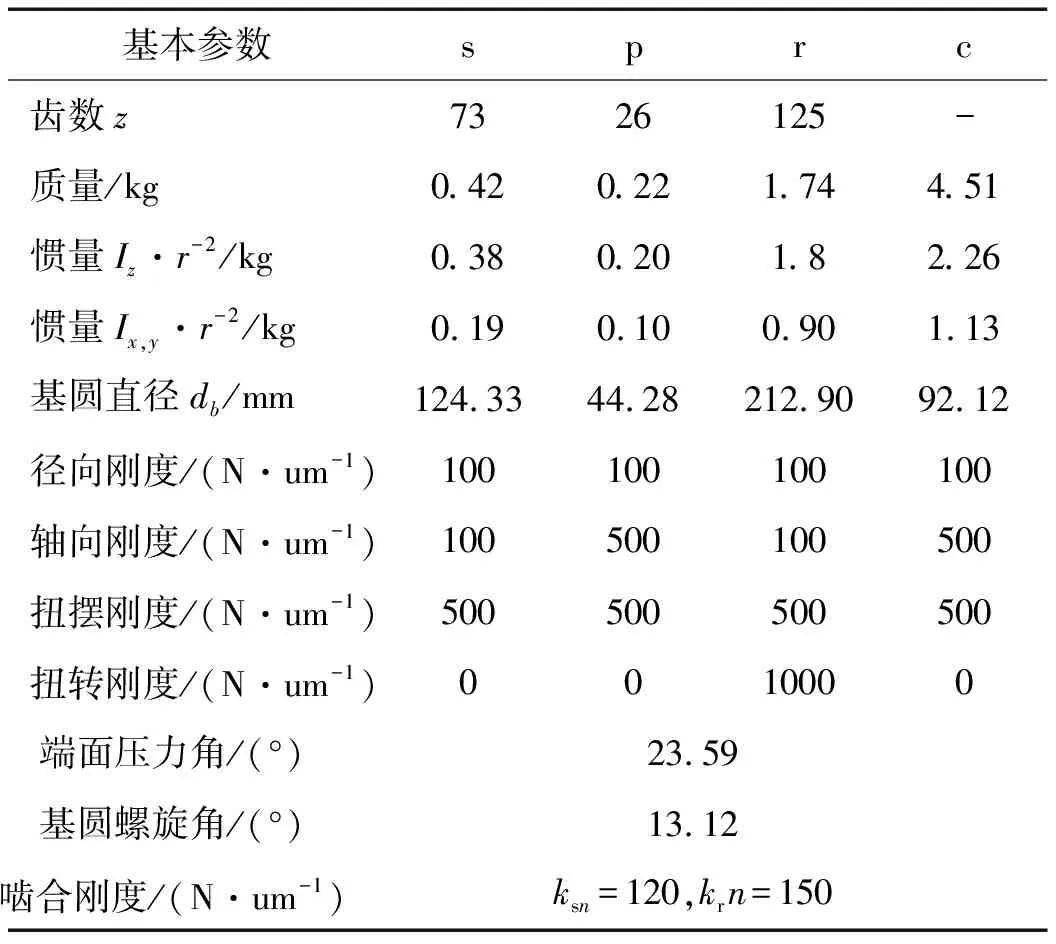
表1 斜齿行星传动算例系统计算参数

2.1 自由振动分析

求解系统运动微分方程的特征值问题，即可获知该类传动的自由振动特性。取系统动力学参数如表1，行星轮数目分别取3、4、5时，可得系统各阶固有频率如表2所示。

根据系统特征值的重根数、中心构件的振型坐标以及各行星轮间振型坐标的比例等特点，可将系统振型划分为3类，即：①轴向平移—扭转振动模式；②径向平移—扭摆振动模式；③行星轮振动模式。各类振型的特点简述如下：

(1) 轴向平移—扭转振动模式： ①各中心构件即太阳轮、系杆和内齿圈只有轴向平移振动和绕z轴的扭转振动，其他方向上的振动均为零；所有行星轮的振型相同。 ②有11个特征值与此模式对应，且相应的特征值均为单根； ③各阶固有频率受行星轮个数影响，其中除零频外，1、2阶固有频率随行星轮个数增加而单调递减，其他阶次固有频率均随行星轮个数增加而单调递增。

(2) 径向平移—扭摆振动模式： ①各中心构件即太阳轮、系杆和内齿圈只有径向的平移振动和绕x、y轴径向扭摆振动，其他方向上的振动均为零； ②有12个特征值与此模式相对应，且相应的特征值均为2重根； ③ 各阶固有频率同样受行星轮个数影响，其中除第1阶固有频率随行星轮个数的增加呈先增后减趋势外，第4阶固有频率随行星轮个数增加而单调递减，其他阶次固有频率均随行星轮个数增加而单调递增。

(3) 行星轮振动模式： ①各中心构件即太阳轮、系杆和内齿圈的扭转、平移运动均为零，且各行星轮的位移为第1个行星轮位移乘以一个系数；②有6个特征值与此模式相对应，其中有5个只在行星轮个数N>3时出现，且重复率为N-3，另一个特征值在行星轮个数N=3时也存在，重复率为N-2。以上各特征值都不受行星轮个数影响。

表2 斜齿行星轮系固有频率

为直观计，图3进一步给出了上述3种振动模式的振型示意图。

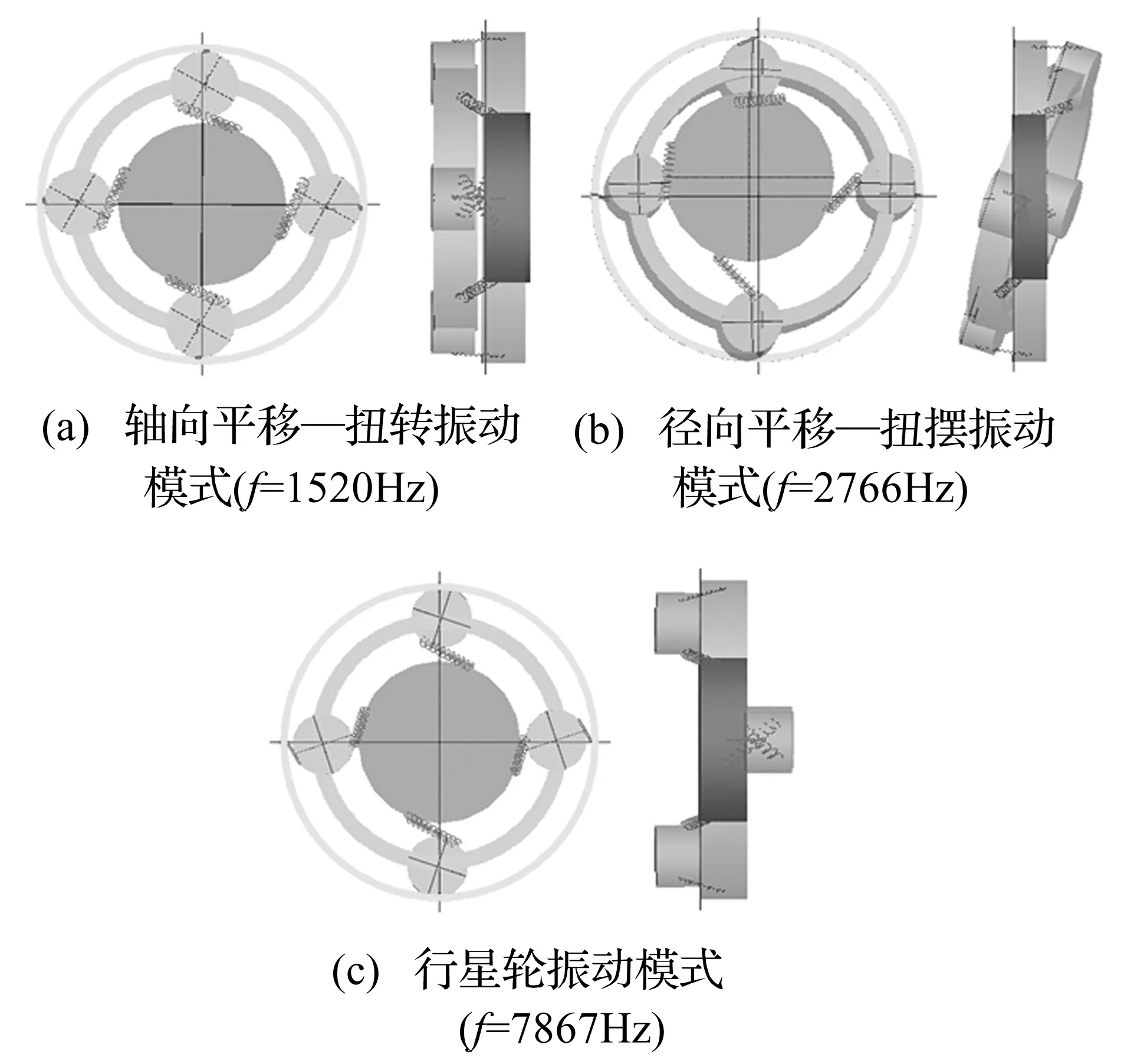
图3 斜齿行星传动振动模式

将表2的仿真结果与采用文献[2-3]的集中参数模型对比，可以发现在同等条件下，两类模型所得的各阶固有频率和振型完全一致，表明本文所建模型的正确性，进而可依托该模型预估斜齿行星轮系的动态特性。

2.2 稳态动力学响应

不妨以表1所示的3行星轮系统为例，采用上述多体动力学模型分析系统的稳态动力学响应。设系统的输入转速恒为1 500 r/min，负载转矩恒为400 N·m。

首先考察无误差情况下，系统的动态啮合力。图4和5分别示出了行星轮系各外、内啮合力及其对应的频谱。

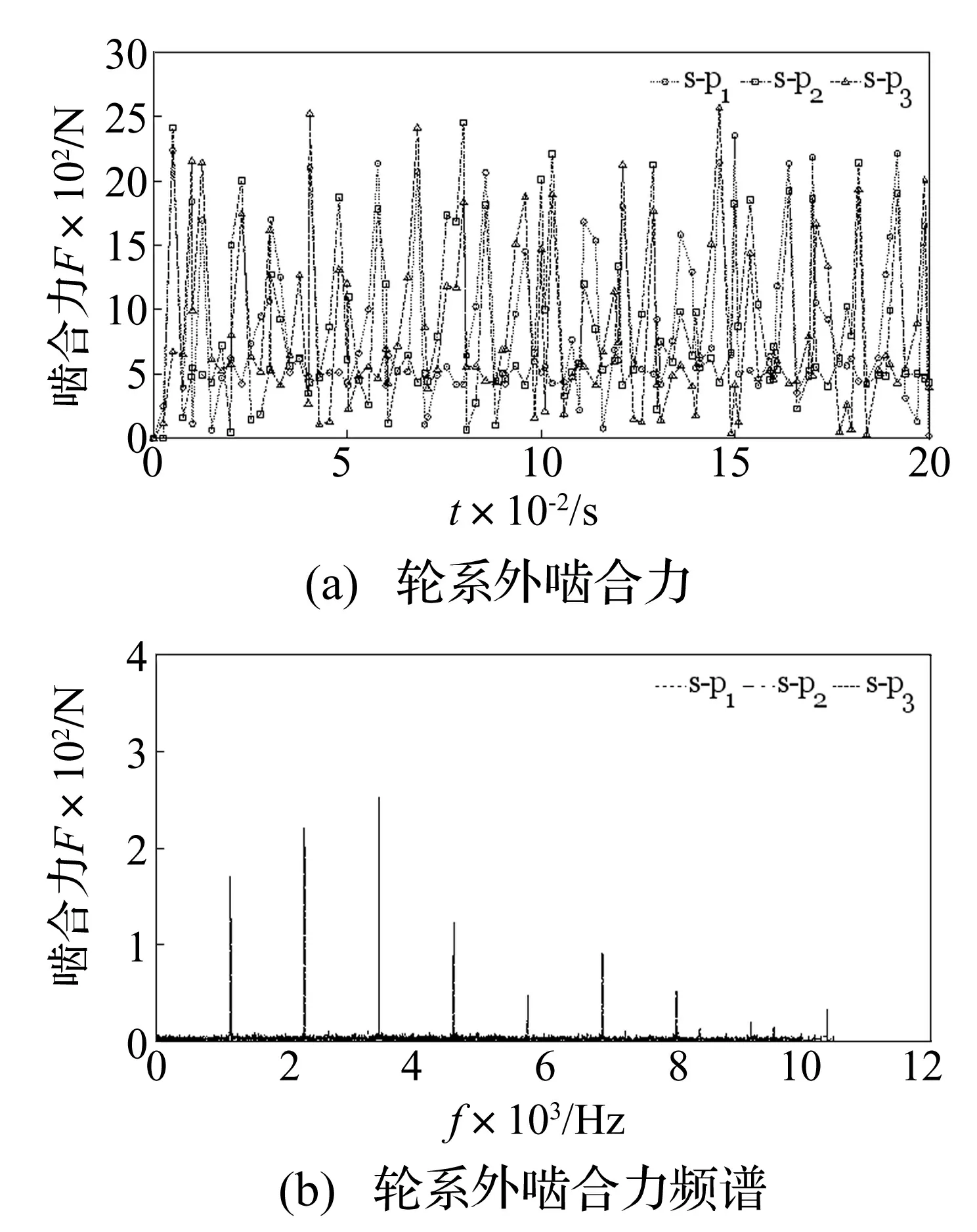
图4 无误差情况下轮系外啮合动态载荷

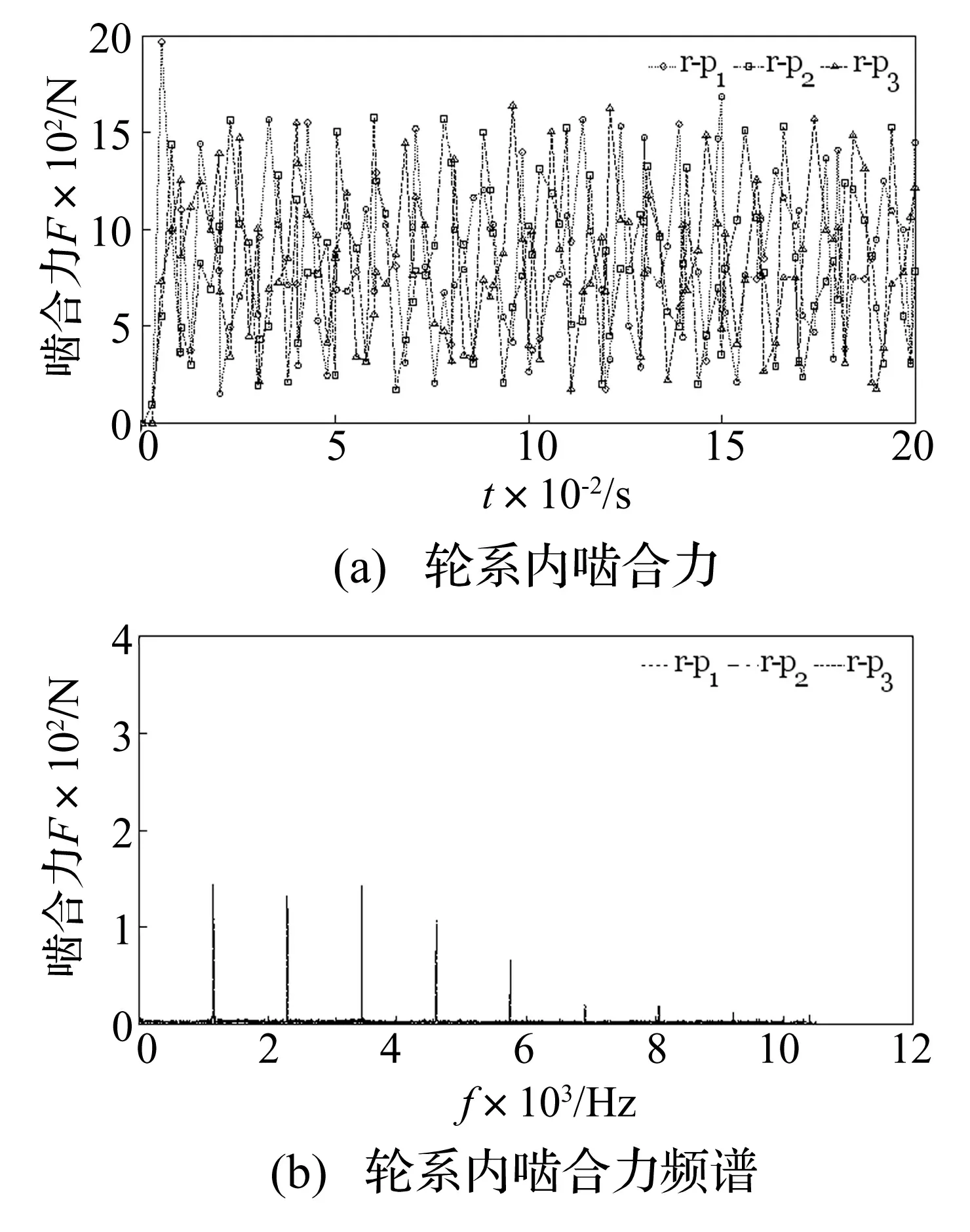
图5 无误差情况下轮系内啮合动态载荷

由图4、图5可知，太阳轮、内齿圈与3个行星轮的动态啮合力变化规律大致相同，只是在数值和相位上略有差别。一个啮合周期内，内、外啮合力的变化显著，说明系统在啮合过程中存在一定的冲击振动。进一步分析可知，上述动态啮合力均围绕831这一均值上下震荡，而这一均值恰为均载条件下轮系静态理论啮合力。

而从啮合力对应的频谱图可知，在1 152 Hz处有一条幅值突出的谱线，它恰好对应于系统的啮频。除此之外，其他几条幅值较大的谱线正好对应啮频的倍频。此点说明啮频激励是引起斜齿行星轮系的主要激励源，这也与前人的研究结论相吻合[3-4]。

3 参数影响分析

斜齿行星轮系的结构复杂，设计参数多，使得该类传动的动态设计和性能优化较为困难。为此，采用灵敏度分析方法，考察系统设计参数对斜齿行星轮系动态特性的影响，希冀为后续系统的性能改善提供一定的理论参考。篇幅所限，下文仅给出构件支承刚度和行星轮周向误差对轮系动态特性的影响规律。

3.1 构件支承刚度

为方便分析，不妨定义一个啮合周期内各啮合力的最大值与静态均值的比例为载荷波动系数，并以符号χi表示。显然，χi越大，表明轮系啮合过程中的振动越强烈。

采用前述的多体动力学模型，进一步分析各构件支承刚度对载荷波动系数的影响。在进行灵敏度分析时，仅改变待分析参数，而保持其他参数不变。

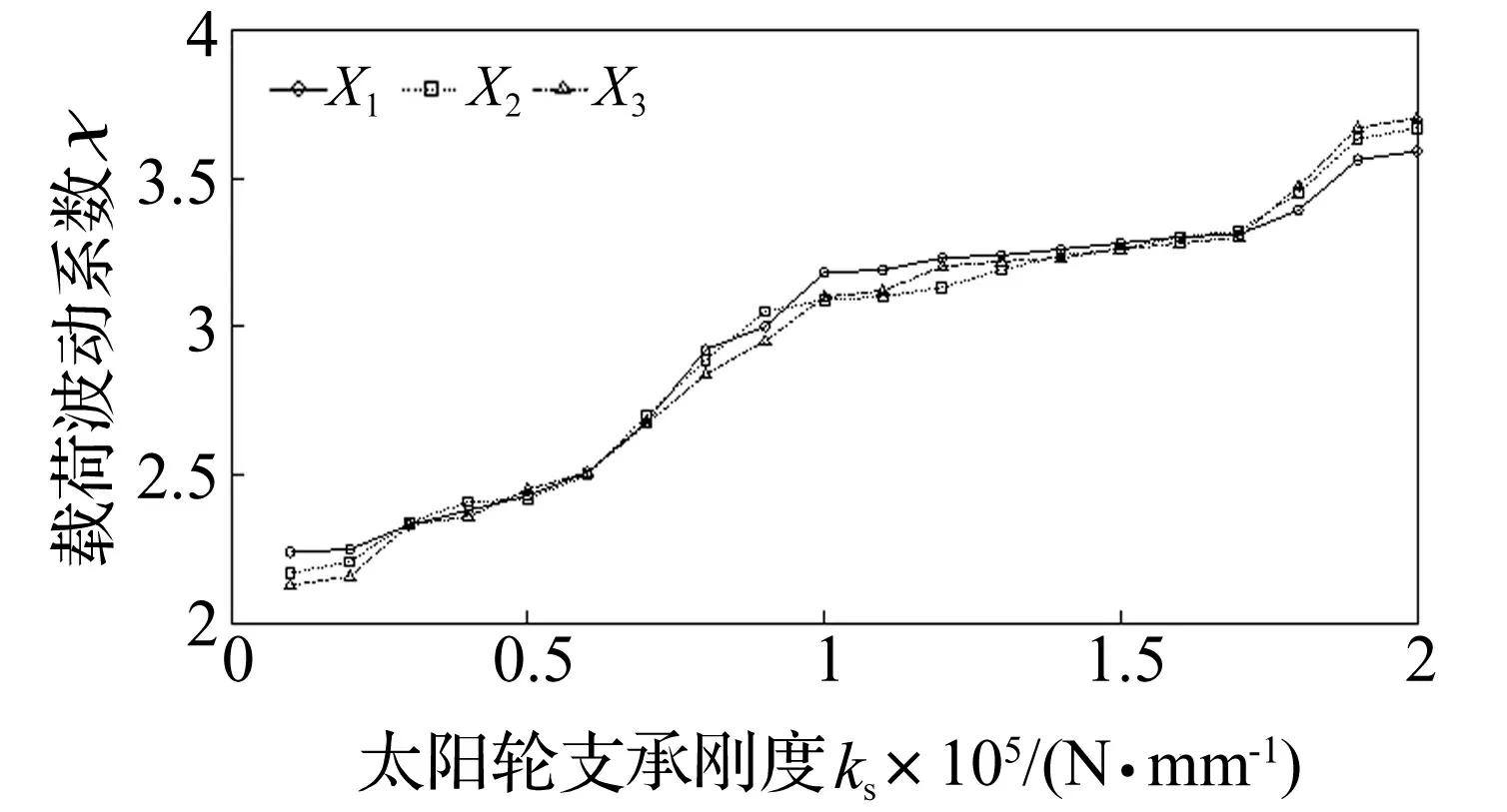
图6 太阳轮支承刚度对载荷波动系数的影响

分析结果表明，各中心构件的支承刚度对系统的均载特性影响显著。随着太阳轮、行星架、内齿圈支承刚度的增加，行星系统的载荷波动系数变大，表明系统的均载特性变差，振动加剧。这其中，太阳轮支承刚度对系统动态性能的影响最大，行星架次之，内齿圈影响最小。由此可见，降低中心构件的支承刚度有利于实现系统均载进而抑制振动。正是基于这一判断，在斜齿行星轮系的工程应用中，可使太阳轮、行星架、内齿圈其中之一浮动，或同时浮动其中的二者，以降低传动系统啮合过程中的振动。限于篇幅，下文仅给出太阳轮支承刚度对载荷波动系数的影响规律。

3.2 行星轮周向安装误差

再来分析行星轮安装误差对系统动态特性的影响。行星轮安装误差可分为径向误差和分度误差。研究表明，与分度误差相比，行星轮径向误差对系统动态特性的影响很小[22]。故下文仅考虑行星轮分度误差对系统动态特性的影响。为便于分析，不妨将行星轮分度误差换算成与其等价的周向误差来表征。以符号eci表示周向误差，并将该误差纳入前述的多体动力学模型。通过求解含误差的动力学模型，可获知相关动力参数。篇幅所限，仅给出其中某一个行星轮(本例为行星轮2)含有35 μm的周向安装误差时(即ec2=35 μm)系统的动态啮合力及其频谱图，其结果如图7、图8所示。

图7 轮系外啮合动态载荷(ec2=35 μm)

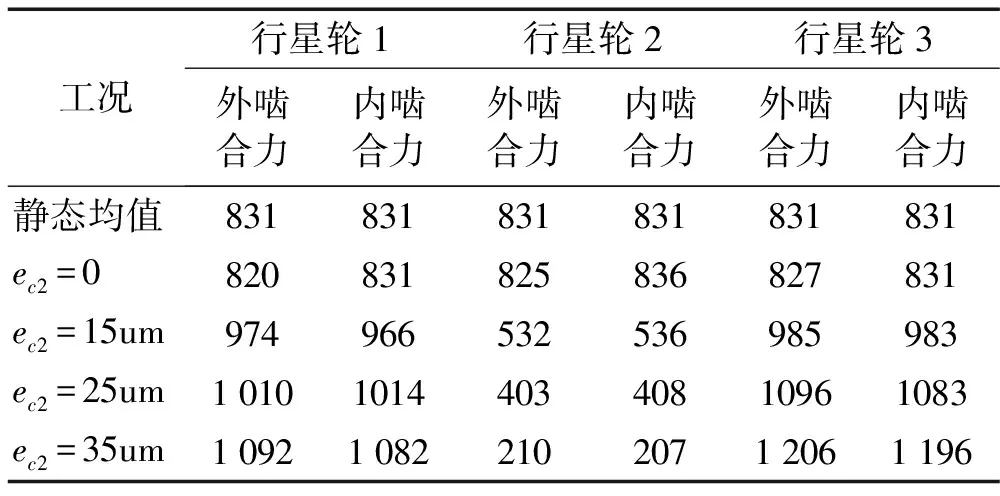
表3 周向安装误差对啮合力的影响(啮合力单位N)

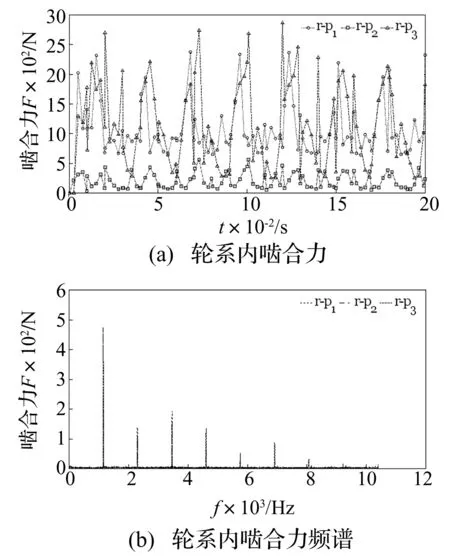
图8 轮系内啮合动态载荷(ec2=35 μm)

进一步分析可知含不同误差工况下系统的动态特性。为方便比较，将各工况下的动态啮合力列表处理，其结果如表3所示。

由上述分析结果可知，行星轮周向安装误差极大地影响斜齿行星轮系的动态特性。就本例而言，周向安装误差的引入，改变了轮系内各啮合副的动态啮合力及各功率流的分配，使得含有误差的行星轮所承担的内、外啮合力均值变小，同时使得其他行星轮的内、外啮合力均值变大；由于周向安装误差使得各行星轮的啮合力均值进一步偏离了其静态理论值，从而使得系统内各啮合力副的载荷波动系数增大，降低了系统的均载性能。进一步的数值分析表明，随着误差量的增大，存在周向安装误差的行星轮所在的功率支路的内、外啮合力均值单调递减，而其他功率支路的内、外啮合力均值单调递增。不仅如此，行星轮周向安装误差还会影响内、外啮合副在啮频倍频处的啮合力。周向安装误差使各内、外啮合力在部分啮频倍频处的幅值增加，而在部分啮频倍频处的幅值减小；且随着周向安装误差量的增大，各功率支路的内、外啮合力在啮频倍频处的变化规律不尽相同。由此可见，斜齿行星轮系的动态特性受行星轮周向安装误差的影响显著，在进行轮系设计、制造和安装时，必须严格控制这一误差环节，以降低系统振动提示传动的动态性能。

4 结 论

(1) 建立了计入多种影响因素的斜齿行星传动的多体动力学模型，并据此分析了传动系统的自由振动特性，其仿真结果与前人的集中参数模型所得结果吻合，表明所建多体动力学模型能正确揭示斜齿行星传动的动态特性。

(2) 快速求解了系统的稳态动力学响应，获得了轮系各环节的动态载荷。仿真结果表明，无误差情况下，轮系各啮合副的动态载荷围绕静态理论啮合力上下波动，且啮频激励是引起系统振动的主要原因。

(3) 中心构件支承刚度对斜齿行星轮系的动态特性影响明显。随着中心构件支承刚度的增加，行星传动的载荷波动系数单调递增，系统动态特性变差。这其中，太阳轮支承刚度对系统动态性能影响最大，行星架次之，内齿圈影响最小。

(4) 斜齿行星传动的动态特性对行星轮周向安装误差较为敏感。行星轮周向安装误差不仅改变各功率支路啮合力的大小和分配情况，还改变了各啮合副在啮频倍频处的幅值。

参 考 文 献

[1]YANG Jian-ming, DAI Li-ming. Survey of dynamics of planetary gear trains[J]. Int. J. Materials and Structural Integrity, 2008, 1(4): 302-322.

[2]Kahraman A. Natural modes of planetary gear trains[J]. Journal of Sound and Vibration, 1994, 173(1):125-130.

[3]杨通强, 宋轶民, 张策, 等. 斜齿行星齿轮系统自由振动特性分析[J]. 机械工程学报, 2005, 41(7): 50-55.

YANG Tong-qiang, SONG Yi-min, ZHANG Ce, et al. Propety analysis of free vibration of helical planetary gear trains[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 50-55.

[4]Kahraman A. Planetary gear train dynamics[J]. Journal of Mechanical Design, 2002, 38(3): 6-9.

[5]Lin J, Parker R G. Analytical characterization of the unique properties of planetary gear free vibration[J]. Journal of Vibration and Acoustics, 1999, 121(2): 316-321.

[6]Lin J, Parker R G. Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J]. Journal of Sound and Vibration, 1999, 228(1): 109-128.

[7]王世宇, 宋轶民, 沈兆光, 等. 行星传动系统的固有特性及模态跃迁研究[J]. 振动工程学报, 2005, 18(4): 412-417.

WANG Shi-yu, SONG Yi-min, SHEN Zhao-guang, et al. Research on natural characteristics and loci veering of planetary gear transmissions[J]. Journal of Vibration Engineering, 2005, 18(4): 412-417.

[8]Lin J, Parker R G. Planetary gear parametric instability caused by mesh stiffness variation[J]. Journal of Sound and Vibration, 2002, 249(1): 129-145.

[9]Lin J, Parker R G. Structure vibration characteristics of planetary gears with unequally spaced planets[J]. Journal of Sound and Vibration, 2000, 233(5): 921-928.

[10]Kiracofe D, Parker R G. Structured vibration modes of general compound planetary gear systems[J]. ASME Journal of Vibration and Acoustics, 2007, 129(2): 1-16.

[11]BU Zhong-hong, LIU Geng, WU Li-yan. Modal analyses of herringbone planetary gear train with journal bearings[J]. Mechanism and Machine Theory, 2012, 54: 99-115.

[12]Kahraman A, Vijayakar S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set[J]. ASME Journal of Mechanical Design, 2001, 123: 408-415.

[13]Kahraman A, Kharazi A A, Umrani M. A deformable body dynamic analysis of planetary gears with thin rims[J]. Journal of Sound and Vibration, 2003, 262: 752-768.

[14]Parker R G. Dynamic response of a planetary gear system using a finite element/contact mechanics model[J]. Journal of Mechanical Design, Transaction of the ASME., 2000, 122: 304-310.

[15]Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J]. Journal of Sound and Vibration, 2000, 236(4): 561-573.

[16]Abousleiman V, Velex P, Becquerelle S. Modeling of spur and helical gear planetary drives with flexible ring gears and planet carries[J]. ASME Journal of Mechanical Design, 2007, 129: 95-106.

[17]Qin D T, Wang J H, Lim T C. Flexible multibody dynamic modeling of a horizontal wind turbine drivetrain system[J]. ASME Journal of Mechanical Design,2009,131: 14501-14508.

[18]Jan H, Frederik V, Ben M, et al. Multibody modeling of varying complexity for modal behavior analysis of wind turbine gearboxes[J]. Renewable Energy, 2011,36:3098-3113.

[19]Lethe G, Guyper , Kang J, et al. Simulating dynamics, durability and noise emission of wind turbines in single case environment[J]. Journal of Mechanical Science and Technology,2009,23:1089-1093.

[20]万长森. 滚动轴承的分析方法[M]. 北京: 机械工业出版社, 1987.

[21]Shabana A A. Dynamics of multibody systems (third edition)[M]. Cambridge University Press, 2005.

[22]Cheon G J, Parker R G. Influence of manufacturing errors on the dynamic characteristics of planetary gear systems[J]. KSME International Journal, 2004, 18(4): 606-621.