基于时间-小波能量谱熵的滚动轴承故障诊断研究

唐贵基， 邓飞跃， 何玉灵， 王晓龙

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

滚动轴承元件(包括外圈、内圈、滚珠)的表面出现局部损伤时，在加载过程中会撞击与其接触的其它元件表面，产生周期性的冲击脉冲力，其振动信号往往表现出非平稳性[1]。在实际工程中，轴承振动信号包含各种干扰噪声，特别是早期故障信号特征微弱易被各种噪声掩盖，小波分析通过伸缩和平移运算对信号进行多尺度细化分析，在不同尺度上描述信号的局部特征，是微弱故障特征信号检测的有效工具[2]。

近年来，许多研究在小波变换的基础上，与信息熵理论相结合，较为有效的对轴承故障进行了分析。艾延廷等[3]将小波变换中表示各个尺度上能量分布的小波能谱熵用来分析旋转机械不同的振动故障状态。曾庆虎等[4]将小波相关滤波和信息熵方法结合，选取最能反映故障特征的小波相关特征尺度熵来判断轴承的运行状态。苏文胜[5]将小波包分解和样本熵结合来提取滚动轴承故障特征。以上方法都是在小波变换的基础上，研究振动信号能量随频率(尺度)的变化特征，鲜有对能量随时间变化特征的研究。

鉴于此，本文提出了时间-小波能量谱熵的诊断方法。首先对信号进行连续小波变换，得到信号能量谱在时间域内分布，振动冲击发生时，各个频率范围内均有冲击信号能量的分布，然后将信号能量谱沿频率轴进行积分，得到随时间变化的小波能量谱值，结合Shannon信息熵理论，提出时间-小波能量谱熵来描述能量谱值随时间变化的复杂程度，显然不同故障下滚动轴承不仅故障特征频率不同，而且其冲击振动沿时间轴的变化也不相同，从而可以有效地对轴承故障进行诊断。

1 基于时间-小波能量谱熵的分析方法

1.1 连续小波变换及时间-小波能量谱

设ψ(t)是一有限能量函数，ψ(t)∈L2(R)，如果其傅里叶变换ψ(ω)满足容许条件：

(1)

ψ(t)称为母小波，将ψ(t)进行伸缩和平移变换，设尺度参数为a，位置参数为b，可以得到一组函数ψa,b(t)：

(2)

ψa,b(t)称为小波基函数。信号x(t)的连续小波变换定义为：

(3)

式中，ψ*(t)是ψ(t)的共轭。根据小波变换的能量守恒原理，有：

(4)

式(4)可以改写为：

(5)

令

(6)

式中Eb定义为时间-小波能量谱。

小波变换系数的大小反映了信号局部与小波函数的相似程度，系数越大，表明信号局部与小波基函数越相似[6]，因此，所选择的小波基函数波形应与滚动轴承振动信号特征相似，Morlet小波是平方指数衰减信号，波形与轴承故障的冲击信号十分相似，所以选择Morlet小波作为小波变换的基函数，其表达式为[7]：

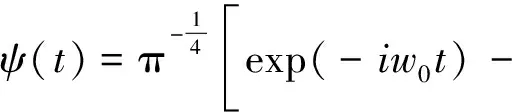
(7)

1.2 Shannon信息熵

(8)

1.3 时间-小波能量谱熵

信号中各个变量的概率分布越均匀，信息熵越大，信息量越大，反之，概率分布越不均匀时，信息熵越小，包含的信息量也越小[8]。本文将连续小波变换中得到的时间-小波能量谱与信息熵理论相结合，提出了时间-小波能量谱熵的计算方法。

(9)

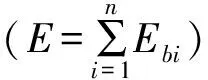
时间-小波能量谱熵表示信号的时间-小波能量谱在时间轴上的分布情况，当分布较为均匀和稳定时，熵值就比较大；当能量谱在某些时刻出现较大峰值，时间域内分布不均衡时，熵值就比较小，不同故障轴承的信号中所包含的冲击振动成分不同，能量谱在时间轴上的分布情况也就不同，熵值大小就会有所区别。

2 滚动轴承的实验分析

2.1 滚动轴承故障模拟试验

滚动轴承实验在试验平台完成，其结构如图1所示。试验采用的滚动轴承型号为N205，受到冲击载荷时，轴承内、外圈极易造成局部损伤，因此在轴承内、外圈上切割沟槽来模拟滚动轴承的局部损伤，如图2所示。试验中，信号采样频率为12 800 Hz，电机转速为1 440 r/min，轴承滚动体个数Z为12个，轴承节圆直径D为39 mm，滚动体直径d为7.5 mm，压力角α=0°，通过计算，外圈故障特征频率和内圈故障特征频率分别如下：

(10)

(11)

图1 试验平台

图2 滚动轴承局部损伤图

2.2 信号分析

因为轴承在不同载荷及工况下的信号变化较大，为了便于统计研究，将原始振动信号xi进行最大值归一化处理，即：

(12)

首先对外圈故障滚动轴承的振动信号进行分析，其时域波形和频谱如图3所示，从波形图中可以看出一些冲击特征，但没有明显周期规律，频谱图中的峰值和外圈故障特征频率也不能完全对应。连续小波变换系数如图4所示，其显示了振动信号在不同的时刻随频率轴的变化情况。

图3 外圈故障振动信号的波形和频谱

图4 外圈故障振动信号小波变换系数图

在振动冲击发生的时刻，信号的时间小波能量谱的幅值会出现峰值，时间-小波能量谱随时间的变化如图5所示。

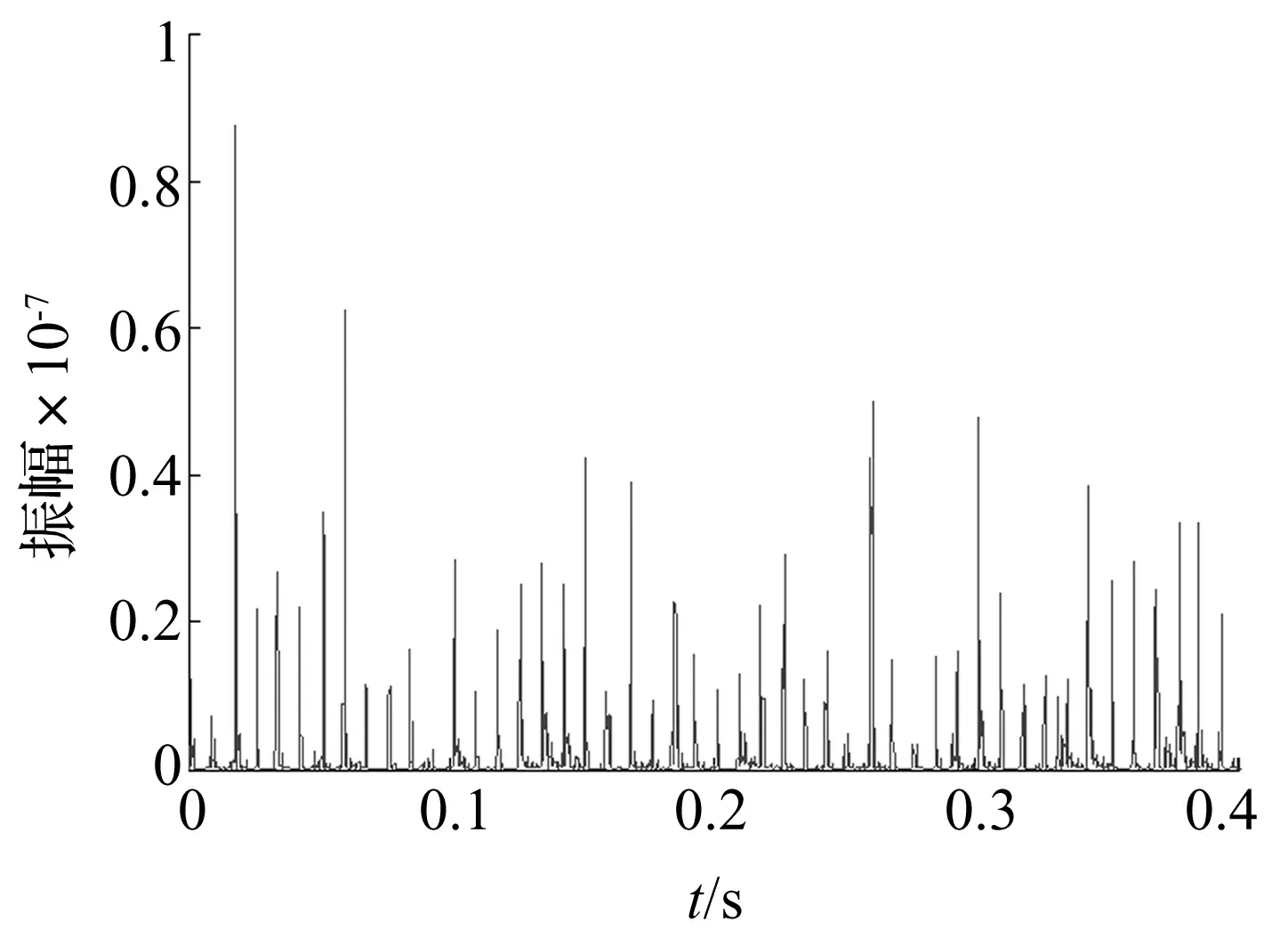
图5 外圈故障时间-小波能量谱时间分布

小波基函数的选择决定了小波变换结果的优劣，为进一步验证所选择的Morlet小波基函数是否合适，对小波变换所得的时间-小波能量谱进行hilbert包络谱分析，结果如图6所示。图6中a点频率为24 Hz，为转轴频频；b点频率为116 Hz为轴承外圈故障的特征频率；c、d、e点为外圈故障特征频率的二倍频、三倍频和四倍频。可见小波变换选取的Morlet小波基函数能较为准确地分析滚动轴承的故障特征。

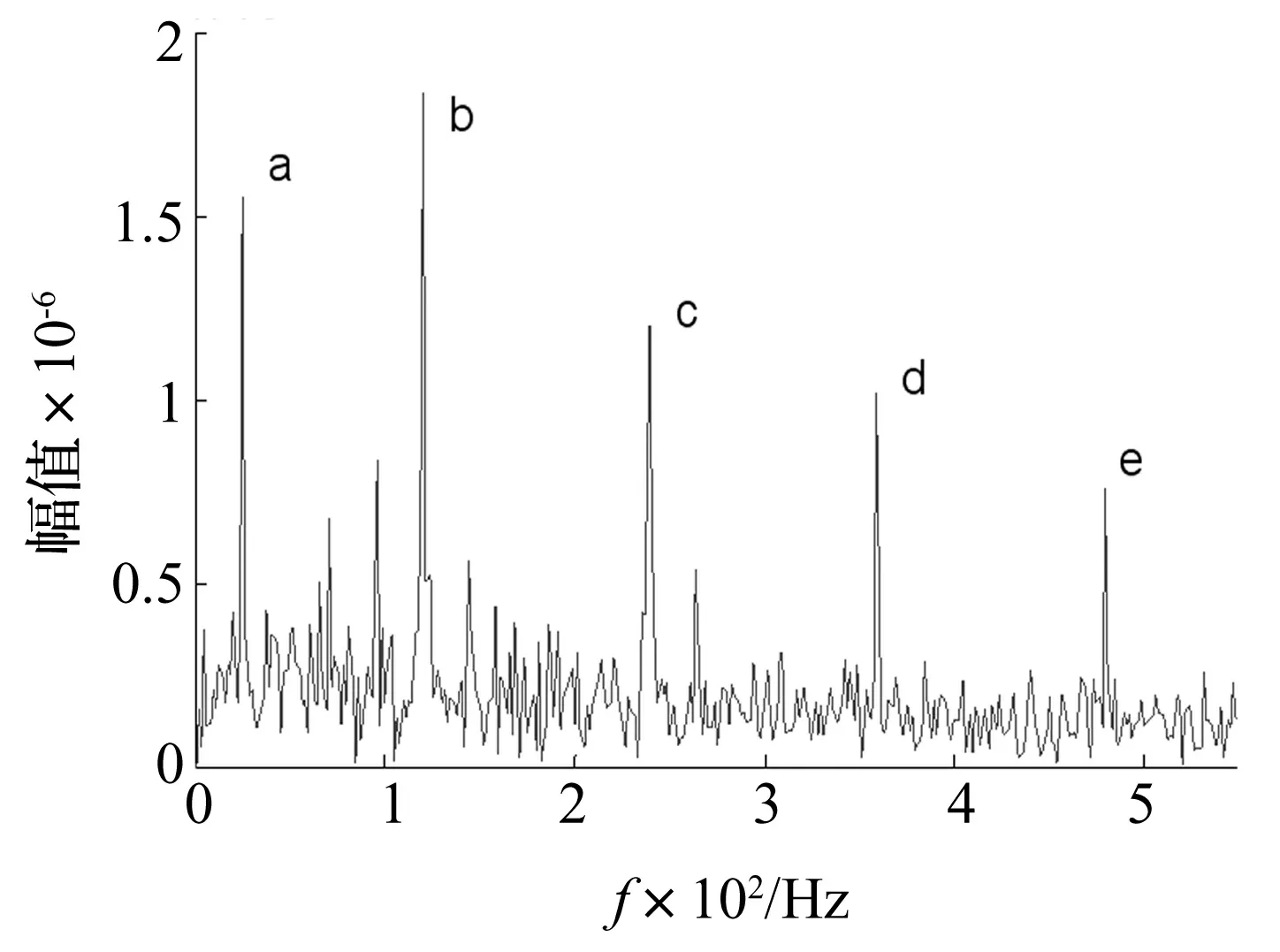
图6 外圈故障信号的包络谱

通过计算，求得在时间段0.32 s内的时间-小波能量谱熵Hwai=2.942 8。

内圈故障轴承信号的波形和频谱如图7所示，连续小波变换系数和时间-小波能量谱随时间分布图分别为图8、图9所示。经计算，在时间段为0.32 s内的时间-小波能量谱熵Hnei=2.556 5。

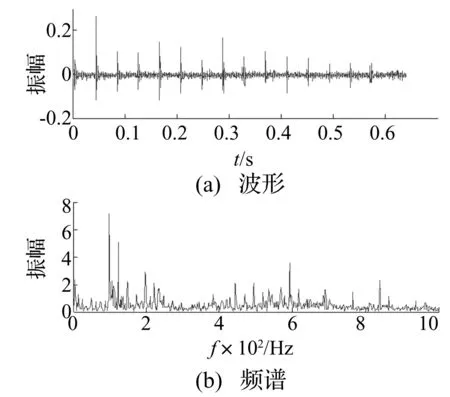
图7 内圈故障振动信号的波形和频谱

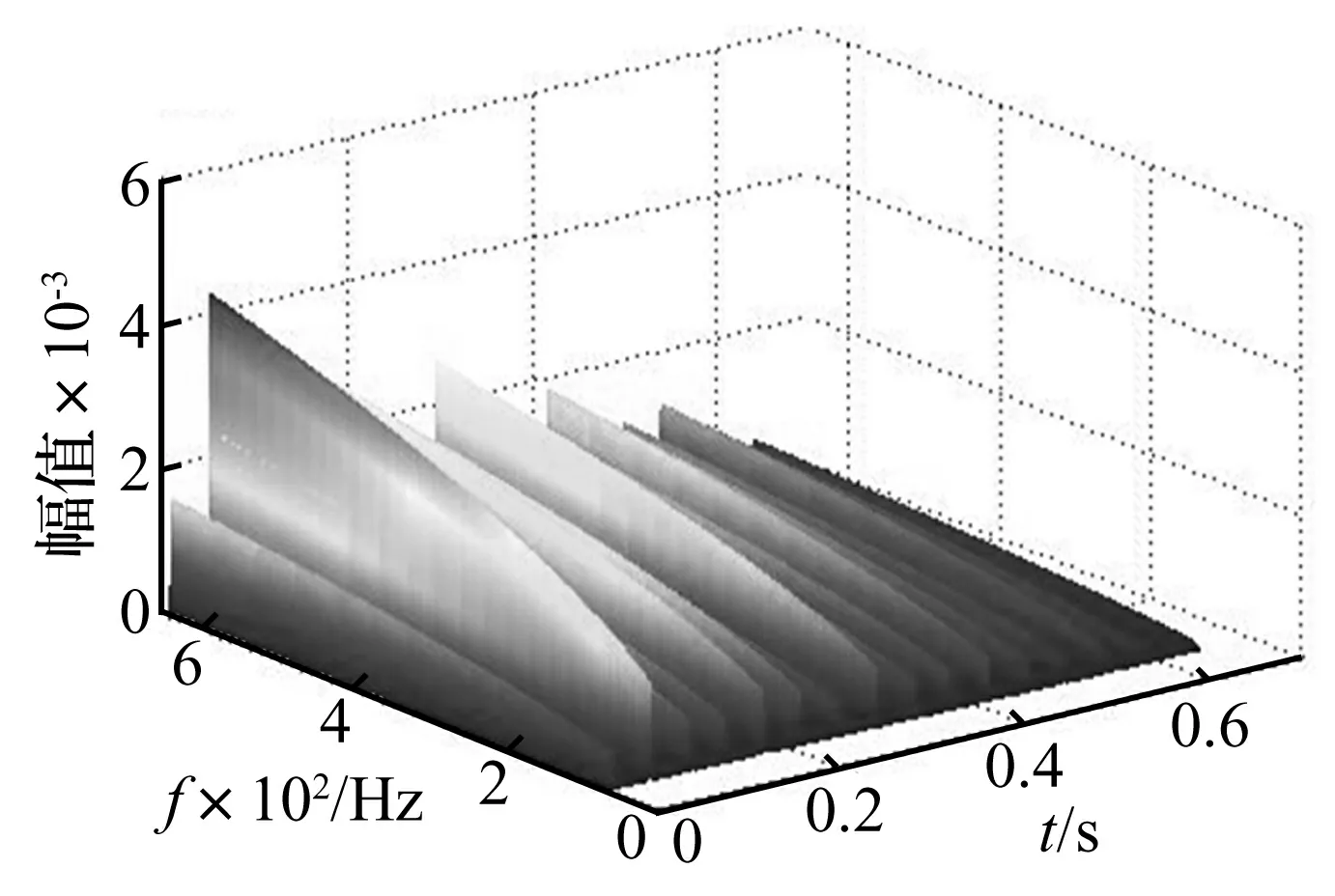
图8 内圈故障振动信号小波变换系数图

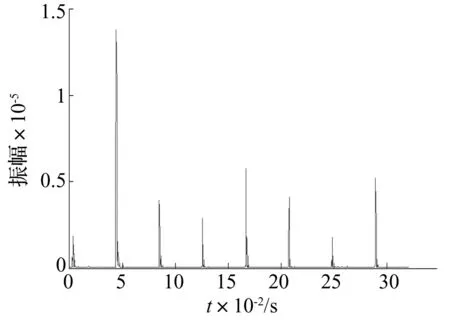
图9 内圈故障时间-小波能量谱时间分布

为更好的进行比较，对正常轴承信号进行分析，其波形、频谱图和时间-小波能量谱随时间分布分别如图10 和图11所示，从频谱图中可以看出没有明显的峰值和故障特征频率相对应，得到在时间段0.32 s内的时间-小波能量谱熵为Hzheng=3.428 5。

图10 内圈故障振动信号的波形和频谱

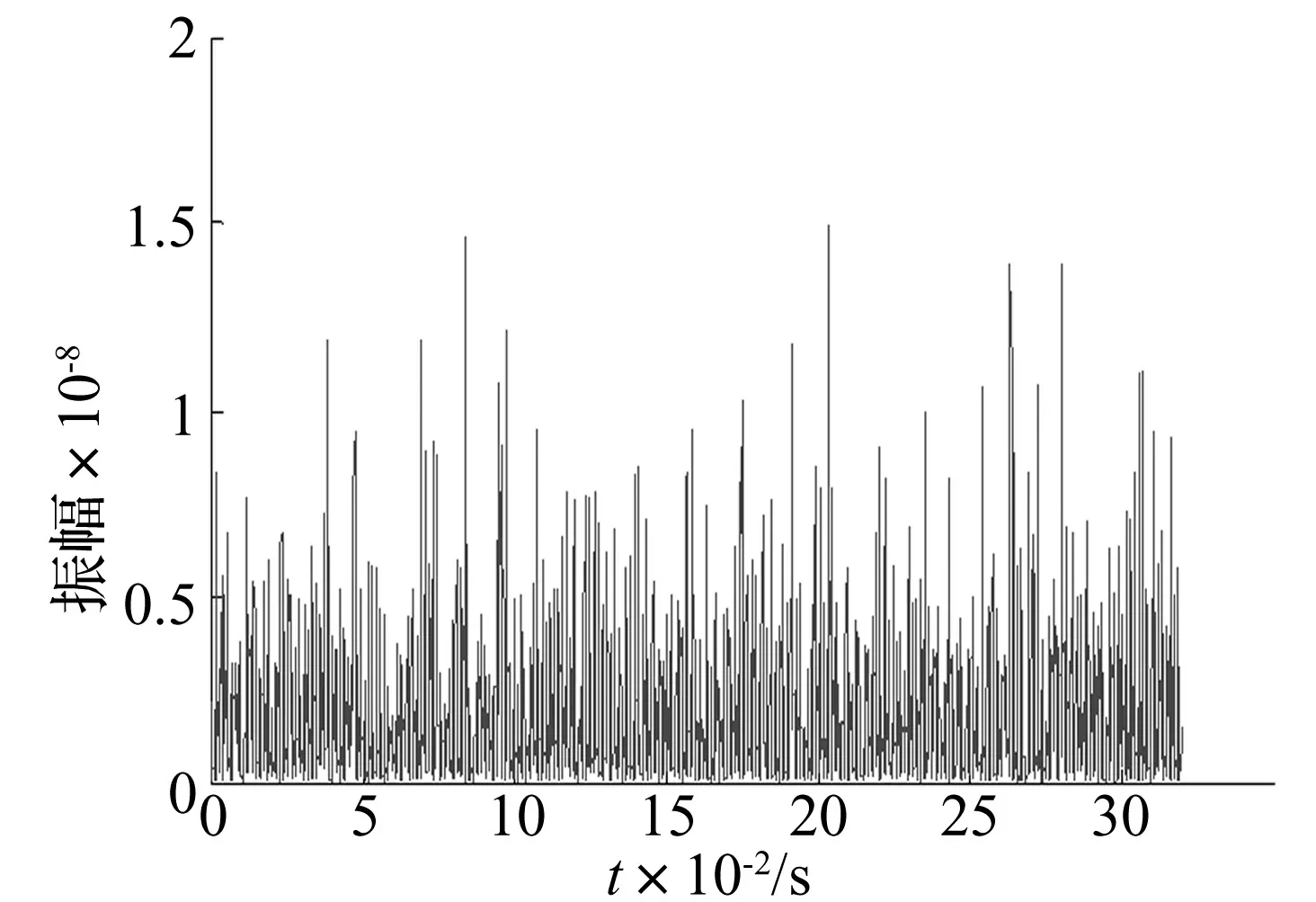
图11 正常轴承时间-小波能量谱时间分布

表1 滚动轴承三种状态下时间-小波能量谱熵

通过以上计算，轴承外圈故障、内圈故障和正常状态下在时间为0.32 s时间段内的时间-小波能量谱熵的结果如表1所示。

表1表明，正常状态下轴承信号的时间-小波能量谱熵要大于另外两种情况，这是因为轴承在正常状态加载运行时没有明显的峰值和滚动轴承的故障特征频率相对应，时间-小波能量谱沿时间轴分布较为平均，通过比较图5、图9和图11也能较为明显地得出。在轴承加载运行过程中，出现外圈故障时，理论上故障位置不发生变化，承载大小也不发生变化[1]，振动冲击的发生较为稳定和均匀；而内圈故障发生时，轴承内圈是随转轴转动的，与滚动体发生接触时局部损伤点的部位会不断的变化，冲击振动的发生是不稳定和不均匀的，从图9中能看出能量谱沿时间轴的分布最为聚集，因此内圈故障的熵值最小。

滚动轴承(正常状态、外圈故障、内圈故障)加载运行过程中，时间-小波能量谱熵的变化如图12所示，图中，三种状态下每个时刻所对应的熵值是不同的，且辨别区间较为明显。

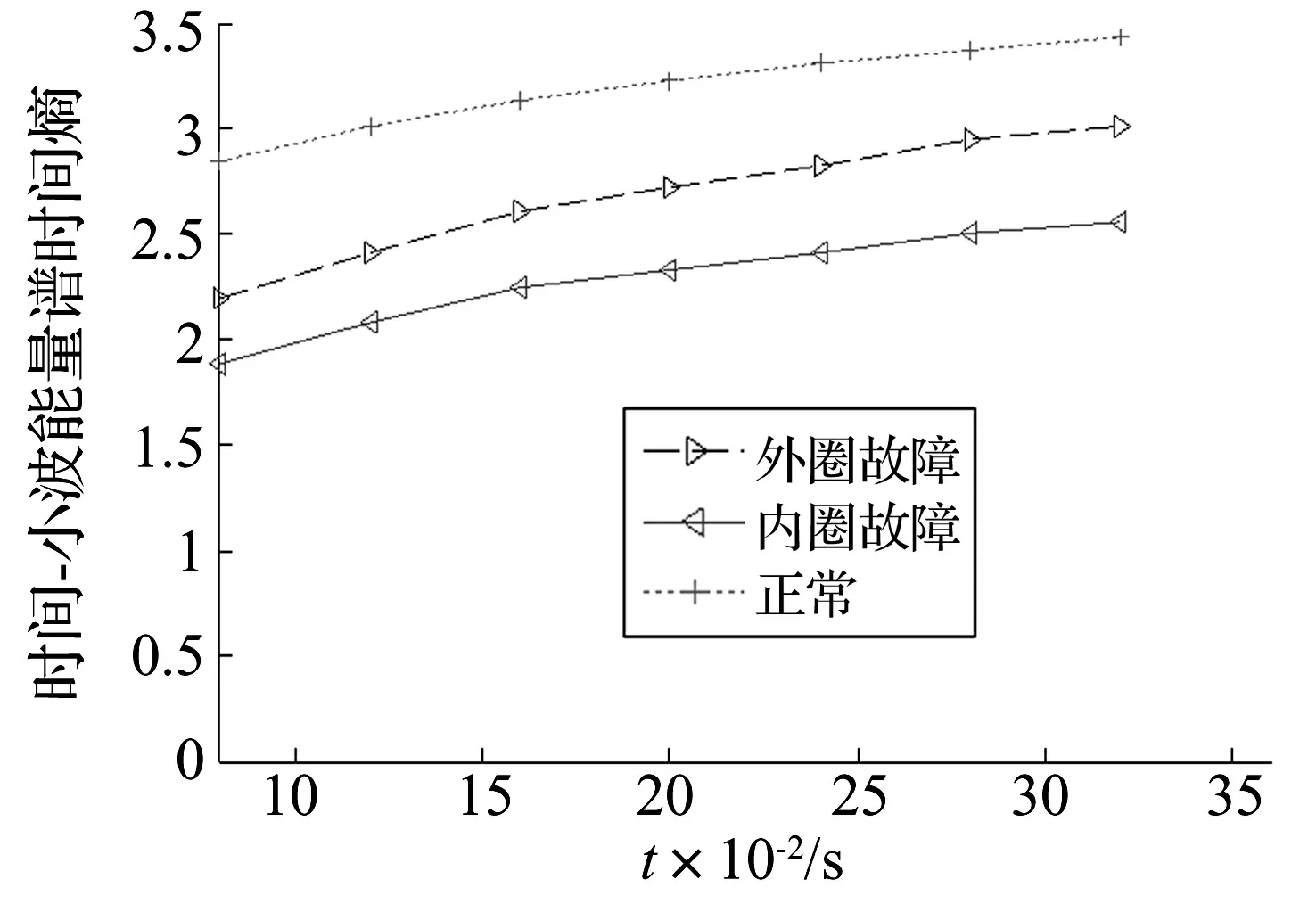
图12 轴承不同状态下时间-小波能量谱熵随时间分布图

小波能谱熵表示的是信号在各个小波尺度上能量的分布情况，不同轴承故障下小波能谱熵不同。为更好进行比较，选取时间段为0.32 s和0.24 s，分别计算本文方法和小波能谱熵在滚动轴承外圈故障、内圈故障和正常状态下的熵值，结果如表2所示。通过比较，时间-小波能量谱熵在滚动轴承不同故障下的区分度要优于小波能谱熵，本文所提出的时间-小波能量谱在时间轴上分布变化要比小波能量谱在各个尺度上的分布变化更为明显。

表2 不同方法性能比较

2.3 SVM故障诊断应用

支持向量机是在统计学习理论基础上发展起来的一种新型机器学习方法，不仅具有优秀的小样本学习能力，而且能较好解决非线性、高维度、局部极小值等问题[9]。因此，本文选用SVM作为故障诊断的分类器，进行故障模式自动识别。支持向量机模型中，核函数选择径向基(RBF)核函数，形式为：

(13)

其中，δ为控制核函数高度的参数，引入惩罚因子C来控制错误分类，参数取值为δ=5，C=150。对正常、内圈故障和外圈故障轴承振动信号分别采样各得61组数据，共有183组，每组数据平均分为10段，每段采样时间为0.32 s，采样点个数为4 096个，求取每段数据的时间-小波能量谱熵作为每个样本的特征向量，则每个样本含有10个特征向量，以这些样本作为SVM的诊断分类样本集。

首先，针对3类模式的数据，在各自的样本集中选取11个样本建立SVM模型，并用这些数据进行SVM模型有效性测试，分类结果的正确性均为100%，可知SVM模型分类效果较好。然后将3类模式剩余的共150组数据作为测试样本，输入到SVM分类器，以分类器输出进行轴承故障自动诊断分类，结果如表3所示。为了进行对比，本文使用相同方式得到了183组以小波能谱熵为特征向量的样本数据，用同样的方法进行SVM训练、测试与故障分类诊断，其与时间-小波能量谱熵的SVM故障分类诊断作比较，结果如表3所示。两类方法的训练样本输入SVM模型时，正确率都为100%，可知SVM模型有较好的学习能力，而且建立的SVM模型对三类故障诊断有较高的识别率，但是因为时间-小波能量谱熵的区分度要优于小波能谱熵，所以以时间-小波能量谱熵为特征向量的SVM故障分类诊断正确率要明显高于以小波能量谱熵为特征向量的SVM诊断，说明基于时间-小波能量谱熵的SVM故障分类诊断效果更好。

表3 支持向量机测试结果

3 结 论

基于连续小波变换和信息熵理论，提出了时间-小波能量谱熵的计算方法，用于滚动轴承故障诊断。时间-小波能量谱熵可以定量描述轴承信号的时间-小波能量谱随时间变化的复杂程度，因为信号能量谱的峰值和故障特征频率相对应，所以不同故障下轴承的时间-小波能量谱在时域内的变化也不尽相同，正常信号的时间-小波能量谱熵要大于发生故障时的熵值，并且建立了时间-小波能量谱熵的SVM故障诊断模型，验证了该方法的有效性。

参 考 文 献

[1]胡爱军，马万里，唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承特征提取方法[J]. 中国电机工程学报，2012，32(11)：106-111.

HU Ai-jun, MA Wan-li, TANG Gui-ji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111.

[2]李宏坤，练晓婷，周帅. 小波尺度谱同步平均在弱信息识别中的应用[J]. 机械工程学报，2013,49(5)：33-38.

LI Hong-kun, LIAN Xiao-ting, ZHOU Shuai. Application on weak information classification by using wavelet scalogram synchronous averaging[J]. Chinese Journal of Mechanical Engineering, 2013,49(5):33-38.

[3]艾延廷，费成巍. 转子振动故障的小波能谱熵SVM诊断方法[J]. 航空动力学报，2011,26(8)：1830-1835.

AI Yan-ting, FEI Cheng-wei. Rotor vibration fault diagnosis method based on wavelet energy spectrum entropy and SVM[J]. Journal of Aerospace Power, 2011,26(8):1830-1835.

[4]曾庆虎，刘冠军，邱静. 基于小波相关特征尺度熵的预测特征信息提取方法研究[J]. 中国机械工程，2008,19(10)：1193-1196.

ZENG Qing-hu, LIU Guan-jun, QIU Jing. Research on approach of prognostics feature information extraction based on wavelet correlation feature scale entropy[J]. China Mechanical Engineering, 2008,19(10):1193-1196.

[5]苏文胜，王奉涛，朱泓，等. 基于小波包样本熵的滚动轴承故障特征提取[J].振动、测试与诊断，2011，31(2):162-166.

SU Wen-sheng, WANG Feng-tao, ZHU Hong. et al. Feature extraction of rolling element bearing fault using wavelet packet sample entropy[J]. Journal of Vibration, Measurement,Diagnosis, 2011,31(2):162-166.

[6]Daubechies I. The wavelet transform , time-frequency localization and signal analysis[J]. IEEE Transaction on Information Theory, 1990, 36(5): 961-1005.

[7]张进，冯志鹏，褚福磊. 滚动轴承故障特征的时间-小波能量谱提取方法[J]. 机械工程学报，2011,47(17)：44-49.

ZHANG Jin, FENG Zhi-peng, CHU Fu-lei. Extraction of rolling bearing fault feature based on time-wavelet energy spectrum[J]. Chinese Journal of Mechanical Engineerin, 2011,47(17):44-49.

[8]王小玲，陈进，从飞云. 基于时频的频带熵方法在滚动轴承故障识别中的应用[J]. 振动与冲击，2012,31(18):29-33.

WANG Xiao-ling, CHEN Jin, CONG Fei-yun. Application of spectral band entropy (SBE) method in rolling bearing fault diagnosis based on time-frequency analysis[J]. Journal of Vibration and Shock, 2012,31(18):29-33.

[9]赵志宏，杨绍普，李韶华.基于Hilbert谱奇异值的轴承故障诊断[J]. 中国机械工程，2013，24(3)346-350.

ZHAO Zhi-hong, YANG Shao-pu, LI Shao-hua. Bearing fault diagosis based on hilbert spectrum and signal value decomposition[J].China Mechanical Engineering, 2013, 24(3):346-350.