应力波作用下弹性直杆动力分叉屈曲研究

毛柳伟, 王安稳, 邓 磊， 韩大伟

(海军工程大学 理学院，武汉 430033)

直杆在轴向冲击下的动力屈曲问题已有大量研究。大多采用放大函数法[1]寻求任意初始缺陷发展最快时对应的屈曲模态，亦称最优模态。经典的放大函数法要求结构具有某种初始缺陷，且假定屈曲发生时杆中各截面处于均匀的轴向受力状态，对高速冲击的杆局部动力屈曲该方法不再适用。直杆在高速冲击载荷作用实验[2-5]表明，屈曲一般发生在结构的局部，该现象的解释需考虑应力波效应。文献[6]认为压应力波作用的结构屈曲伴会随应力波在结构中传播或反射波与入射波叠加发生。文献[7-8]认为考虑应力波效应时结构屈曲与应力波传播会耦合。文献[9]对直杆动力屈曲研究认为直杆横向位移出现振荡解向发散解的转变标志着屈曲开始，而在屈曲模态选取中却采用随时间放大最快的模态，该模态显然非文中的屈曲开始时刻模态。文献[10]将直杆横向位移出现振荡解向发散解转变时刻记为临界屈曲时刻，认为在分叉的一瞬间，杆并未横向惯性效应。文献[11]在受刚性质量块轴向撞击杆动力屈曲分析中屈曲判断准则与文献[10]相同，忽略了分叉瞬间杆的横向惯性效应，但在阶跃载荷作用下杆的动力屈曲中却记入横向惯性影响。文献[12]据能量率守恒原理获得波前附加约束条件，用双特征参数法求解压应力波作用下直杆动力屈曲问题，指出考虑惯性效应所得临界应力值是忽略惯性效应计算值的2.5倍。文献[13]在对应力波作用下直杆的动力屈曲研究中用临界屈曲时间作为动力屈曲指标，认为动力屈曲中临界屈曲时刻的角色与静力失稳中临界失稳载荷相当。文献[14]对考虑应力波的直杆分叉屈曲的研究，计算中仅考虑阶跃载荷。

动态加载包括阶跃载荷与时变动载荷，两种载荷作用下直杆动力屈曲尚无统一判别形式。本文分析表明屈曲模态中放大最快模态对应的位移同时能满足屈曲控制方程及附加约束条件[12]，可统一双特征参数法与最优模态法思想，并建立直杆动力屈曲求解的数值方法。该方法可用于时变动载荷作用并考虑应力波效应直杆动力屈曲研究，且对阶跃载荷及时变动载荷引起应力波作用的屈曲问题具有统一屈曲判别形式。通过对实验计算对比说明，该方法准确可靠。

1 弹性压应力波作用下直杆动力屈曲控制方程

图1 压应力波作用下杆中轴向力(应力波未反射)

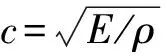
(1)

或用能量率守恒原理[15]，得直杆屈曲控制方程为：

(2)

2 弹性压应力波作用下直杆动力屈曲准则

式(1)、(2)为对同一问题的不同描述。用式(1)求解杆中压应力波为阶跃载荷时，可得屈曲模态的解析形式，故便于求解；但对时变动载荷，如质量块撞击引起杆中应力波非均匀分布情况，用式(1)则不能求解。用式(2)求解时一般需设定屈曲模态，屈曲模态设定的形式会对计算结果产生一定影响。为克服此困难，本文在对弹性直杆在应力波作用的动力分叉屈曲进行分析、探讨基础上，统一双特征参数理论与最优模态法思想，采用有限元离散，建立求解时变动载荷作用、考虑应力波效应直杆动力屈曲理论方法。

将直杆用两节点Euler-Bernouli梁单元离散，单元的形函数为：

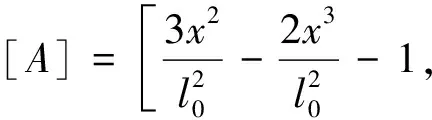
单元几何刚度矩阵为：

弯曲刚度矩阵为：

一致质量矩阵为：

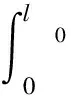
其中：l0为单元长度；[C]=[A]′；[D]=[A]″。

按几何非线性有限元理论，直杆动力屈曲控制方程可表述为：

(3)

式中：[M]为结构整体质量矩阵；[K]，[Kσ]分别为结构整体弯曲刚度矩阵及几何刚度矩阵；{δ}为整体节点位移阵。

令整体节点位移阵为：

(4)

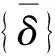
(5)

式(5)为压应力波作用下直杆发生动力分叉屈曲的特征方程。由式(4)可知λ>0时结构存在发散解；若屈曲模态一定，特征参数λ将直接决定屈曲模态放大程度。λ为关于临界屈曲长度l(l=ctcr)及轴向分布载荷的函数，临界屈曲时载荷在杆中分布一般为已知，故λ为关于临界屈曲长度的函数，令：

(6)

即可得一定外载作用下，结构屈曲发展最快模态(即最优模态)对应长度。

分离变量，将杆屈曲位移函数写成：

w(x,t)=Y(x)T(t)

(7)

其中：Y(x)为屈曲模态；T(t)为时间函数。

将式(7)代入式(2)，分离变量，得：

(8)

3 弹性压应力波作用下直杆动力屈曲求解

为验证本文理论的正确性，对实验进行计算(计算时逐渐增加应力波传播长度，每一长度可得一个数组，取该数组中最大值，若该值大于零时对其开方得对应该长度的λ，否则对其绝对值开方，开方所得值的负数即为对应该长度的λ，由此所得λ能反映结构屈曲时模态放大程度)。

3.1 算例1

文献[11]中用空气动力枪加载，分别对撞击端为夹支与简支约束试件进行轴向冲击实验。试件用45号钢，弹性模量E=201 GPa，屈服极限σs=417 MPa，材料密度ρ=7 890 kg/m3，长度L=460 mm。矩形截面：h=5 mm，b=10 mm。杆在应力波反射前发生屈曲，应力波在杆中传播过程可用阶跃载荷表示：

(9)

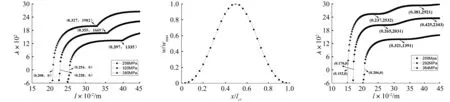
图2 撞击端夹支试件特征值λ与长度l关系

为便于对比，引入无量纲量：

(10)

由表1知两端固支直杆静力失稳临界力参数约为4；一端简支，一端固支直杆静力失稳临界力参数约为2。与相应长度直杆静力失稳临界力参数吻合良好。由于撞击端固支下一阶临界力参数为8.92[11],撞击端简支情况下一阶临界力参数为5.09。而理论计算[12]得撞击端固支、简支下一阶临界力参数分别为10、5，相应的动力特征参数分别为3、2；撞击端简支情况下二阶临界力参数为13，相应的动力特征参数为6。对比可知，本文计算结果与文献吻合较好。由图2、图4看出，冲击载荷越大，临界屈曲长度越小。

表1 试件1～6临界力参数及动力特征参数值

3.2 算例2

由文献[2]，矩形截面细长直杆一端固定、一端被一质量M=0.369 kg的刚性体以v0=6.3 m/s速度撞击，据实验装置直杆撞击端为简支。试件(记试件7)为Ni-Cr钢，截面尺寸b=8.7 mm，h=0.63 mm，弹性模量E=210 GPa，材料密度ρ=7 778 kg/m3，σs=310 MPa。杆在应力波反射前发生屈曲，应力波在杆中传播过程可表示为[9]：

(11)

经计算，λ与l关系见图6。由图6看出：l=0.023 5 m时λ=0，该点与相应长度直杆静力失稳状态对应；一阶最优屈曲模态对应的临界长度为0.036 5 m；二阶最优模态对应的临界长度为0.059 m；三阶最优模态对应的临界长度为0.081 5 m。

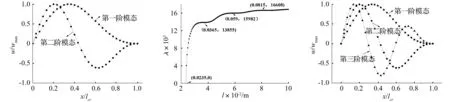
图5 试件4一、二阶屈曲模态

试件7前三阶屈曲模态计算结果见图7。整理图6中数据，记σ=ρcv0，代入式(10)计算结果见表2。

表2 试件7临界力参数及动力特征参数值

由表2可知一端简支、一端固支直杆静力失稳临界力参数约为2，与相应长度直杆静力失稳临界力参数吻合良好。而文献[11]中该临界力参数为5.09，文献[12]中理论计算撞击端简支一、二、三阶临界力参数分别为5、13、25，动力特征参数分别为2、6、12。经对比可看出本文计算结果与文献[11-12]结果吻合较好。

4 结 论

(2) 经与有关文献实验数据比较表明，该方法准确可靠，可用于时变动载荷及阶跃载荷时考虑应力波效应直杆动力屈曲研究。

参 考 文 献

[1]Abrahamson G A,Goodier J N. Dynamic flexural buckling of rods within an axial plastic compression wave[J]. Journal of Appl Mech ,1966 ,33 (6):241-247.

[2]Hayashi T, Sano Y. Dynamic buckling of elastic bars,second report,the case of high velocity impact[J]. Bulletin of JAME,1972,15(88):1176-1184.

[3]Lindberg H E, Florence A L. Dynamic pulse buckling-theory and experiment[M]. Defence Nuclear Agency, Washington, Contract No. DNA 001-78-0287, Martinus Nijhoff, Norvell, MA, 1987.

[4]TANG Li-qun, ZHU Zhao-xiang. Impact buckling and postbuckling of slender elastic bars[M].Beijing:Peking University Press, 1994: 43-54.

[5]Ari-Gur J, Weller T, Singer J. Experimental and theoretical studies of columns under axial impact[J]. Int. Journal of Solids. Struct, 1982,18(7):619-641.

[6]朱兆样.应力波引起的弹性结构屈曲准则[A].塑性力学和地球动力学文集[C].北京:北京大学出版社,1990:56-70.

[7]Denzil G. Vaughn, John W. Hutchinson. bucklewaves[J]. European Journal of Mechanics A/Solids,2006,25:1-12.

[8]Vaughn D G, Canning J M, Hutchinson J W.Coupled plastic wave propagation and column buckling[J]. Journal of Applied Mechanics,ASME,2005,72(1):139-146.

[9]Lepik ü L O. A contribution to bifurcation analysis of elastic-plastic beams[J]. Int. J. Impact Engng,1998,21(1-2): 35-49.

[10]韩 强,武际可,张善元,等.直杆中应力波传播引起的分叉问题[J].力学学报,1998, 30(4):414-422.

HAN Qiang, WU Ji-ke, ZHANG Shan-yuan. Bifurcation caused by the stress wave in columns[J].Acta Mechanica Sinica,1998,30(4):414-422.

[11]韩志军.直杆的撞击屈曲及其应力波效应的实验和理论研究[D]. 太原：太原理工大学,2005.

[12]WANG An-wen, TIAN Wen-ying. Twin-characteristic-parameter solution for dynamic buckling of columns under elastic compression wave[J]. Int. J. Solids Struct,2002,39(4):861-877.

[13]Wooseok Ji, Waas A M. Dynamic bifurcation buckling of an impacted column[J]. International Journal of Engineering Science, 2008,46(10):958-967.

[14]钟炜辉,郝际平,雷 蕾,等.考虑应力波的轴心压杆冲击分岔屈曲研究[J].振动与冲击,2010, 29(10):201-205.

ZHONG Wei-hui, HAO Ji-ping, LEI Lei, et al. Impact bifurcation buckling of an axial compression bar with stress wave[J]. Journal of Vibration and Shock,2010, 29(10): 201- 205.

[15]王礼立,余同希,李永池.冲击动力学进展[M].合肥：中国科学技术出版社,1992:157-176.