随机激励下重载车辆空气悬架参数多目标优化

庞 辉， 彭 威， 原 园

(西安理工大学 机械与精密仪器工程学院，西安 710048)

随着高速公路快速发展及对运输效率要求提高，载重汽车使用愈加广泛。在保证汽车动力性与操纵稳定性前提下，对路面的破坏已成重型载货汽车的主要问题。由于路面激励引起车辆垂向振动，导致车辆行驶平顺性变差，对路面产生较强冲击破坏力。空气悬架可根据车辆质量及路面状况自适应调整空气弹簧刚度及阻尼系数，使车辆平顺性达到最优，改善驾驶员的舒适性，且可减轻车辆零部件的损坏程度，提高车辆使用寿命[1]。

目前，遗传算法(Genetic Algorithm，GA)广泛用于求解多模式优化问题全局解，如车辆主动/半主动悬架优化问题[2-5]，GA算法亦用于求解控制器增益及优化控制问题[5-6]。为提高车辆行驶平顺性，重载车辆常用空气悬架系统，其空气弹簧刚度、阻尼小于轮胎刚度及阻尼(指两者刚度不在同一数量级)，且轮胎与空气弹簧刚度、阻尼具有一定非线性，使车辆空气悬架系统亦有较强非线性特征。若能对轮胎与空气弹簧刚度、阻尼参数进行优化与匹配，则可提高整车性能。对载重车辆悬架参数优化已有大量研究[2-9]，但优化设计方法、思路与实际工程应用仍有差距。如已有优化方法存在：①目标优化函数较少，只考虑某一种路面的优化；②多个子目标函数的权重系统分配较随意，会导致优化目标函数局部过早收敛，多采用各目标加权合成一个适应度进行优化策略。

本文以某载货汽车空气悬架为研究对象，从提高车辆行驶舒适性、减小轮胎对路面动载荷目的出发，构建该车1/2车辆模型的多目标优化模型，采用一般遗传优化算法及改进的多目标自适应优化算法对车辆空气悬架参数进行优化，并将两种优化结果对比分析。

1 随机路面模型

路面不平度指道路表面偏离理想平面，影响车辆动力性、行驶质量、路面动载荷三者数值特征，通常用功率谱密度描述路面统计特征[10-12]，据功率谱密度，路面分8级。

路面不平度统计特征可用路面速度功率谱密度描述为：

(1)

其中：n0=0.1 m-1为参考空间频率；Gq(n0)为参考空间频率n0下路面功率谱密度值，称路面不平度系数，单位m3。

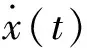
(2)

由式(2)知，路面速度功率谱密度幅值在整个频率范围内为一常数，即 “白噪声”，其幅值大小仅与路面不平度系数Gq(n0)及车速u有关。对平稳随机路面激励，其路面模型为高斯随机过程。由此，可得路面仿真计算的一般公式为：

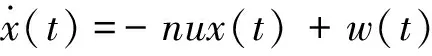
式中：w(t)为matlab白噪声；x(t)为路面随机位移激励；n为所选路面空间频率，A级路面n=0.14，B级路面n=0.13，C级路面n=0.12。

基于matlab/simulink环境建立的车辆前轮路面仿真模型见图1，其输出作为求解1/2车辆模型的输入信号。需要说明的是，后轮路面相对前轮输入信号有一定时间延迟t1，t1=(a+b)/u。

图1 前轮路面随机仿真模型

2 1/2车辆模型

某载货汽车简化力学模型见图2，其中Z2为车身垂向位移；θ为车身俯仰角；Z1f，Z1r为前、后轮垂向位移，为该1/2车辆模型的4个自由度；Z0f，Z0r为前、后轮路面不平度输入信号，由图1获得。车辆及空气悬架参数见表1。

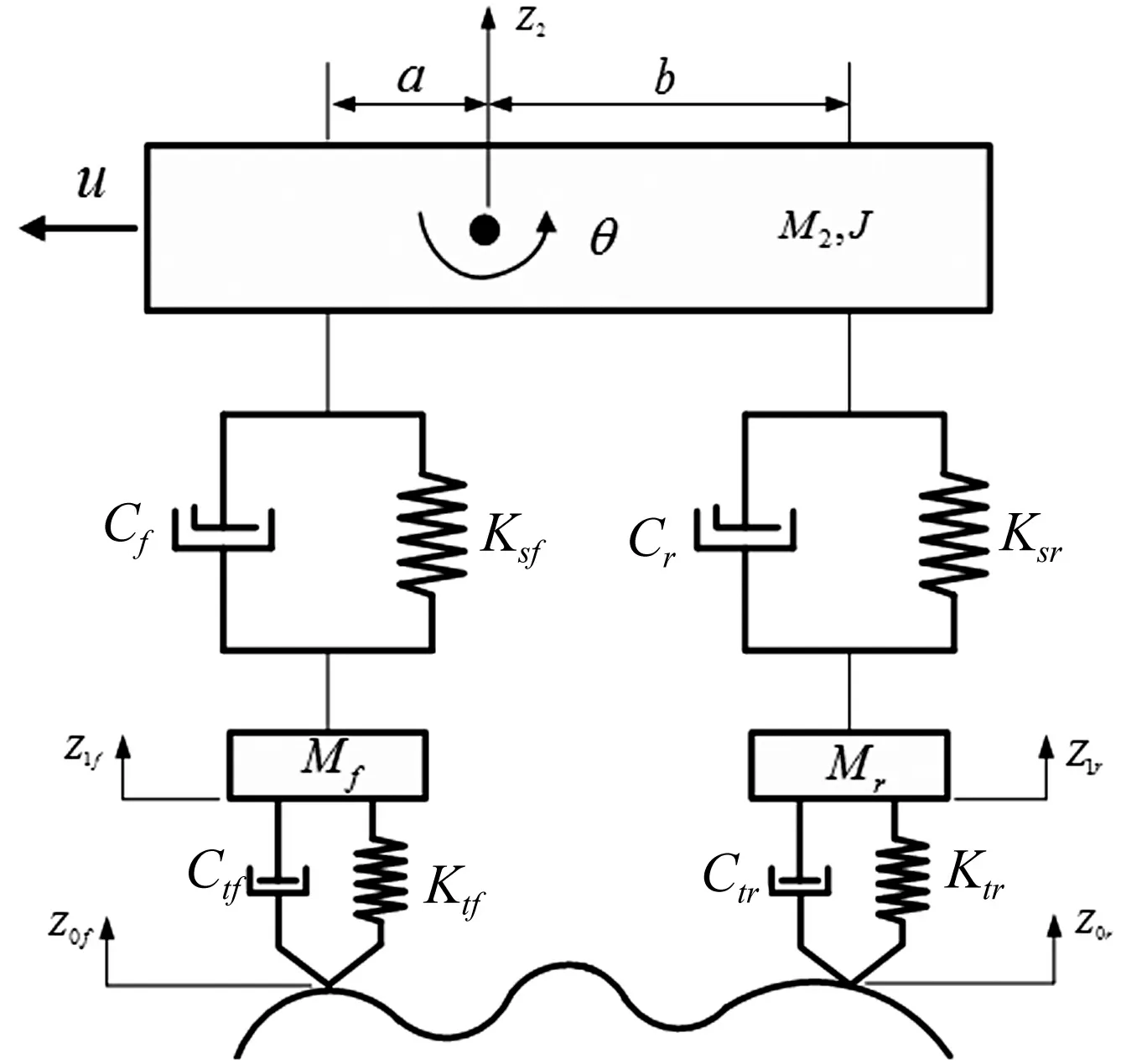
图2 车辆四自由度振动模型

表1 车辆参数

车辆行驶中前后轮输入为平稳随机路面激励，且作用于前后轮两处。据图2的1/2车辆模型悬架系统动力学模型建立动力学方程为：

(3)

其中：

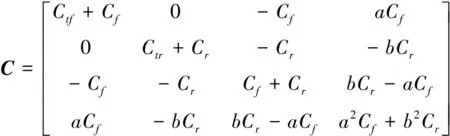
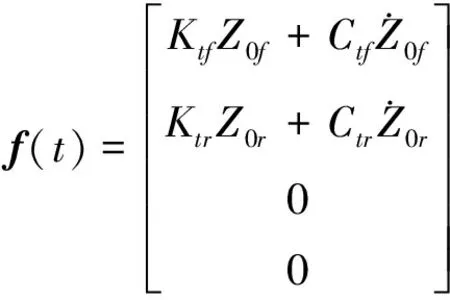
前、后轮胎对路面的瞬时动载荷分别为：

(4)

(5)

前、后轮胎对路面的动载荷均方根值为：

(6)

(7)

车身垂直加速度均方根值为：

(8)

式中：N为采样点总数。

3 悬架参数多目标优化

3.1 目标函数

为提高汽车行驶平顺性、减少轮胎对路面的破坏，以车身垂向加速度均方根值a(X)为汽车平顺性评价指标，以前、后轮对路面的动载荷均方根值f1(X),f2(X)为动载荷对路面破坏程度评价指标。为控制随机因素所致性能波动，以a(X)，f1(X)，f2(X)三目标函数的统计方差为目标函数，对载荷汽车在A、B、C级路面上的行驶稳定性进行优化，均值目标函数、方差目标函数各9个，共18个，见表2。

3.2 设计变量

设计变量取：X=[x1x2x3x4]T=[KsfKsrCfCr]T，结合实际情况与经验取值范围见表3。

3.3 约束条件

为保证货车行驶中车辆、货物的安全性，悬架动挠度所受碰撞器限制在安全范围内，即：

g1(X)=Z2-Z1f+6σ(z2-z1f)≤Dmax

(9)

g2(X)=Z2-Z1r+6σ(z2-z1f)≤Dmax

(10)

式中：Dmax为允许最大动挠度，据陕汽奥龙4×2牵引车悬架限位行程取80 mm。

表2 悬架参数优化的目标函数

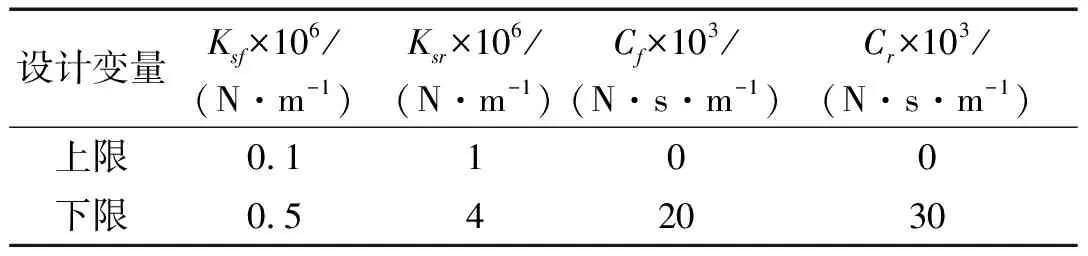
表3 设计变量的范围

3.4 优化过程及结果

图3 自适应遗传算法计算流程图

遗传算法模拟达尔文生物进化论的自然选择与遗传学机理的生物进化过程计算模型，为模拟自然进化过程搜索最优解方法。通过搜寻一个或多个目标函数最小(最大)值，创建个体种群模拟自然选择(本文为半主动车辆悬架控制输入)，选父代产生子代，且胜任的个体存活(胜任个体作为下一代优化使用)。遗传算法主要特点为全局搜索能力强、不易陷入局部最优，尤其适用于复杂、非线性问题[14]。但传统的遗传算法在处理多目标优化问题时，往往对多个目标函数作加权线性组合，将多目标转换为单目标处理。其存在两明显缺点：① 目标权系数分配存较大主观性；② 在计算过程中易陷入局部极小点导致过早收敛，无法找到理想值。对此，本文采用改进的自适应遗传优化算法，计算流程见图3。改进有：

(1) 随机初始化种群。即据随机参数约束限制初始化种群，保证参数选择的真实性。

(2) 适应度计算。即采用适应值重新分配，优化过程中适应度据目标函数值计算，满足约束条件个体代入目标函数，目标函数值即为适应度，否则适应度为零；不满足条件个体以绝对概率淘汰，避免权重取1/18的主观性及优化目标函数值过早陷入局部极小点导致过早收敛。

(3) 选择。即据轮盘赌策略累加适应值，选择交叉父代，随机选择母代。

(4) 交叉、变异。交叉为单点交叉，种群交叉、变异概率值并非始终不变，据适应值变化而变化，交叉变异概率Pc，Pm确定算式为：

(11)

式中：k1,k2,k3,k4为给定合适值，据此可避免一般遗传算法局部寻优缺点，使所求值无限逼近理想值，更好达到寻优目的。本文取k1=0.5，k2=0.9，k3=0.02，k4=0.05，f，f′为适应值；favg为平均适应值。

经优化计算，得悬架参数优化结果见表4。由表4中看出，优化后后轮刚度值有所增加，阻尼值有所减小。

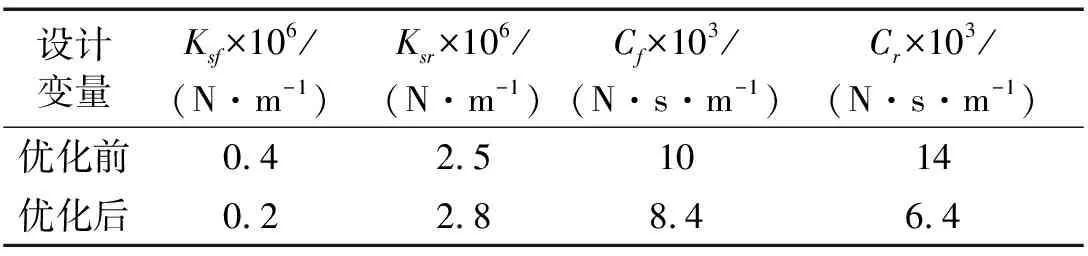
表4 优化前后悬架参数对比

采用一般优化与改进多目标自适应优化方法计算所得目标函数统计均值结果对比见表5。

表5 一般优化与多目标自适应优化目标函数统计均值对比

表6 一般优化与多目标自适应优化目标函数统计方差对比

表7 常规GA与MOGA优化目标函数值对比

对比分析表5～表7中优化计算结果不难看出，相比一般遗传算法：① 利用本文所提算法计算所得车身垂向加速度、前后轮动载荷有效值约减小10%；② 经多目标自适应遗传优化算法优化后所得垂向加速度、前后轮动载荷有效值方差约降低50%，改善幅度较大；③ 对比表7优化前后目标函数值知，优化后目标函数值改善度降低57.03%，证明了本文算法的有效性，达到多目标优化目的。

为将算法收敛与计算量对比分析，传统GA算法优化过程为：初始化种群→解码→计算适应值→交叉和变异→得出最优结果；本文的改进MOGA算法增加了适应值重新分配原则、轮盘赌策略、自适应交叉及变异等环节(图3)。计算用时上，传统遗传算法需3天，MOGA算法则需4天。算法收敛上，初始化种群50、迭代次数100时，MOGA遗传算法结果基本稳定，而传统遗传算法计算结果变动较大，出现局部最优解情况。

为直观对比一般遗传优化与改进多目标自适应遗传优化计算结果，A级路面激励下优化前后垂向加速度、前后轮动载荷结果见图4～图6，限于篇幅，略去B级、C级路面计算曲线对比图。

图4 A级路面垂向加速度对比曲线

4 结 论

本文建立的重载车辆空气悬架参数多目标优化模型，采用一般遗传算法与改进的多目标自适应遗传优化算法对该悬架进行优化计算，结论如下：

(1) 建立的4自由度1/2车辆空气悬架多目标优化模型，采用统一目标函数法对车辆悬架参数进行多目标优化，不仅可提高车辆行驶舒适性，且可减小重载车辆对路面的动载荷，减轻路面损伤。

(2) 较一般遗传优化算法，采用改进的多目标自适应遗传算法计算所得垂向加速度，前、后轮动载荷改善幅度大，悬架参数变化小。

(3) 本文所用方法与优化算法对其它类型车辆悬架参数优化计算亦具参考价值。

参 考 文 献

[1]Bhandari V, Subramanian S C. Development of an electronically controlled pneumatic suspension for commercial vehicles[C]. International Conference on Power, Control and Embedded Systems (ICPCES), Allahabad, India,2010.

[2]TANG Chuan-yin, GUO Li-xin. Research on suspension system based on genetic algorithm and neural network control[J]. Journal of The Open Mechanical Engineering, 2009,3:72-79.

[3]Crews J H,Mattson M G, Buckner G D. Multi-objective control optimization for semi-active vehicle suspensions[J].Journal of Sound and Vibration, 2011, 330:5502-5516.

[4]李海林,王 铁,申晋宪,等. 被动空气悬架导向机构仿真与优化[J]. 机械传动, 2012,36(2):50-56.

LI Hai-lin,WANG Tie,SHEN Jin-xian,et al.Simulation and optimization of guide mechanism of air suspension[J]. Journal of Mechanical Transmission,2012,36(2):50-56.

[5]吴晓君,郑 超,路 超,等.基于遗传算法和ADAMS的麦弗逊悬架优化研究[J].工程设计学报,2012,19(4):274-277,282.

WU Xiao-jun,ZHENG Chao,LU Chao,et al. The research on optimization of macpherson suspension based on genetic algorithm and ADAMS[J]. Journal of Engineering Design, 2012,19(4):274-277,282.

[6]Michalewicz Z,Janiko C,Krawczjk J. A modified genetic algorithm for optimal control problems[J]. Computers and Mathematics with Applications, 1992,23(2):83-94.

[7]庞 辉,方宗德,李红艳,等.某载重卡车悬架参数优化及试验研究[J].振动与冲击,2012,31(8):92-95,106.

PANG Hui, FANG Zong-de, LI Hong-yan, et al. Optimization of suspension parameters and test research on a heavy-duty truck[J]. Journal of Vibration and Shock, 2012,31(8):92-95,106.

[8]徐道临,张 林,周加喜. 重型矿用自卸车油气悬架参数优化[J].振动与冲击,2012,31(24):98-101,107.

XU Dao-lin, ZHANG Lin, ZHOU Jia-xi. Parametric optimization of hydro-pneumatic suspension of a heavy mining dumper[J]. Journal of Vibration and Shock,2012, 31(24):98-101,107.

[9]王 涛，陶 薇. 考虑随机因素的汽车悬架参数多目标稳健优化[J]. 振动与冲击, 2009, 28(11):146-149.

WANG Tao, TAO Wei. Multi-objective robust optimization of automobile suspension parameters considering random factors[J]. Journal of Vibration and Shock,2009, 28(11):146-149.

[10]ISO2631-1:1997(E), International standards origination, mechanical vibration and shock evaluation of human exposure to whole-body vibration Part1, General requirements[S].

[11]余志生. 汽车理论(第5版)[M]. 北京：机械工业出版社, 2009.

[12]段虎明,石 峰,谢 飞,等. 路面不平度研究综述[J]. 振动与冲击,2009,28(9):95-101.

DUAN Hu-ming,SHI Feng,XIE Fei, et al. A survey of road roughness study[J]. Journal of Vibration and Shock,2009,28(9):95-101.

[13]陈杰平, 陈无畏, 祝 辉, 等. 基于Matlab/Simulink的随机路面建模与不平度仿真[J]. 农业机械学报, 2010,41(3): 11-15.

CHEN Jie-ping, CHEN Wu-wei, ZHU Hui, et al. Modeling and simulation on stochastic road surface irregularity based on Matlab/Simulin[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010,41(3): 11-15.

[14]杜 恒,魏建华．基于遗传算法的连通式油气悬架平顺性与道路友好性参数优化[J]．振动与冲击，2011，30(8):133-138.

DU Heng, WEI Jian-hua. Parameters optimization of interconnected hydro-pneumatic suspension for road comfort and road-friendliness based on genetic algorithm[J]. Journal of Vibration and Shock,2011，30(8):133-138.