多排任意排列的弹性桩屏障对平面P波或SV波多重散射

孙苗苗， 夏唐代

(1.浙江省水利河口研究院,杭州 310020； 2. 浙江省水利防灾减灾重点实验室， 杭州 310020;3.浙江大学 软弱土与环境岩土工程教育部重点实验室,杭州 310058；4.浙江大学 岩土工程研究所，杭州 310058)

人工振动对人体、环境均有不同程度污染。为隔离或减少人工振动，使损害降至最低，在被保护建(构)筑物与环境振源之间设置屏障成为治理环境振动所致污染主要手段之一。目前有两种隔振屏障形式：①连续屏障形式，如空沟、填充沟、混凝土墙等，但在地下水位较高、人工波较长的软土地区，连续屏障的施工或隔振效果均不理想；②非连续隔振屏障，即排桩、排孔等，能克服连续屏障的不足。

非连续屏障对弹性波散射研究起步较晚。Woods[1]运用全息照相技术对瑞利波入射下圆孔屏障隔振进行研究，提出非连续屏障的设计依据。Liao等[2]进行水中桩列、孔列隔振比例模型试验，认为桩土刚度比对隔振效果影响较大。Massarsch等[3]对水泥石灰排桩进行现场试验研究。Avilés等[4-5]采用波函数展开法对P波、S波及R波入射下单排实心桩的散射问题进行理论研究。Kattis等[6]据纤维增强复合材料近似均质化理论，将非连续屏障等效为连续屏障，对非连续屏障设计可参照连续屏障设计法则。Tsai等[7]采用频域边界元方法对三维单排非连续屏障振动隔离进行分析，认为桩间距对屏蔽效果影响较大。蔡袁强等[8-9]由Boit饱和波动方程出发，运用波函数展开法研究饱和土中单排桩对弹性波的隔离问题。

以上研究非连续屏障对平面波隔离问题的解析解法中均只考虑单重散射。而单重散射假设的不足在于忽略散射体即桩列作为整体相互间相干相位关系，仅在桩间距较大时才正确。实际工程中，通常采用的排桩间距较小，排桩体系作为整体屏障起作用，各桩之间相互影响。多个任意半径、任意排列的弹性桩屏障对平面P、SV波散射问题的精确解尚未见报道。

本文基于全空间各向同性介质中任意位置、任意半径的圆柱形散射体对弹性波多重散射理论[10-12]，对柔性桩屏障设其桩土边界满足弹性位移及应力边界条件，求解平面P、SV波入射下散射及透射波场，获得总波场解。对单排及多排弹性桩屏障进行数值计算与参数分析，并通过将该解退化至刚性桩的解验证此弹性桩理论体系，对实际工程隔振设计提出建议。

1 理论模型

1.1 模型

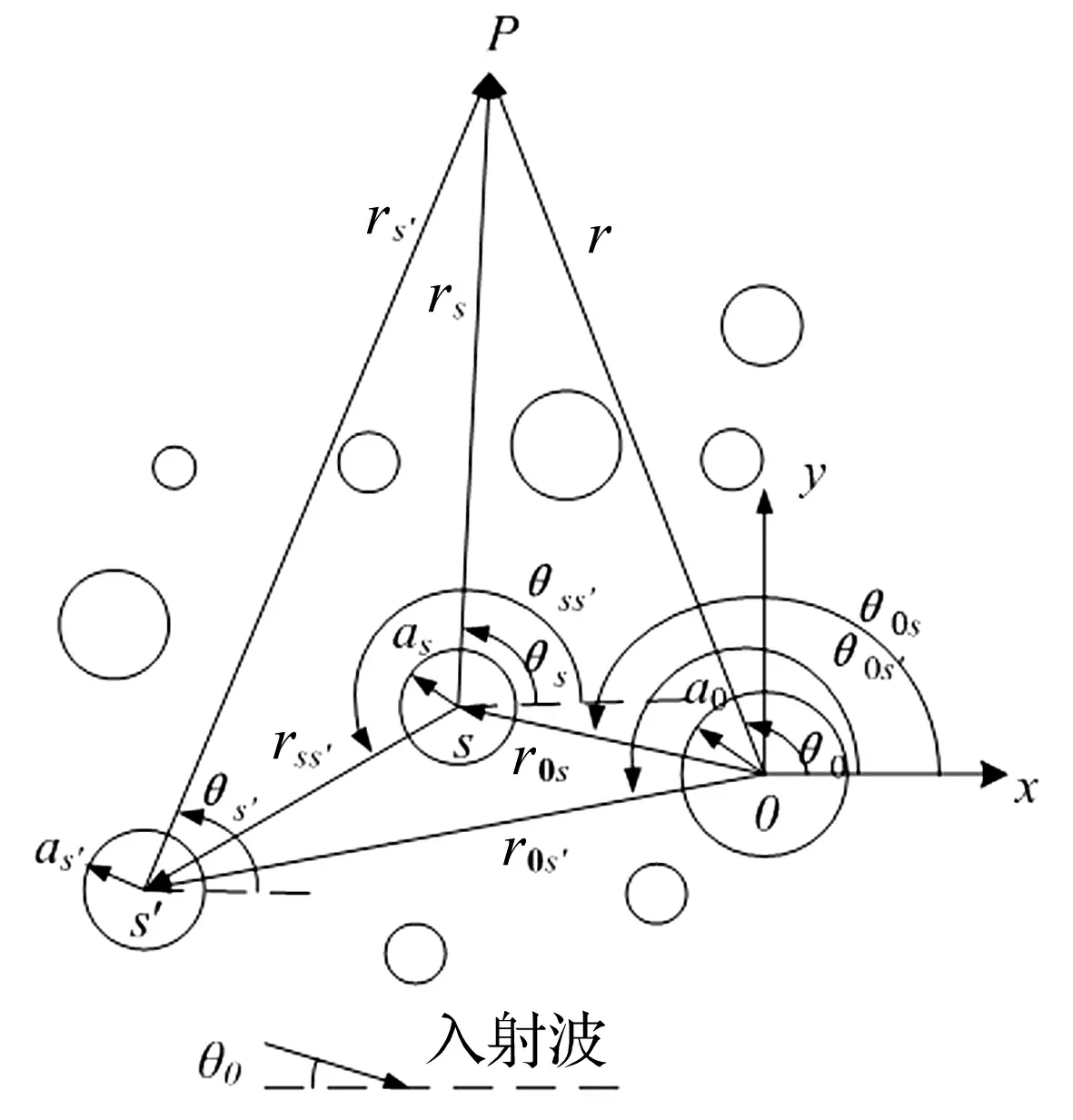
图1 任意排列、任意半径圆柱形散射体对平面波散射分析模型

任意排列、任意半径的圆柱散射体几何分析模型见图1。设散射体外介质为无限、各向同性的均质弹性体，介质Lamé常数为λ，G；质量密度ρ。图中各散射体均分布于该介质中。散射体轴线设为无限延伸，该问题可简化为二维平面应变问题。

为研究振动隔离问题，选圆柱散射体后一远场P点作为研究对象。定义圆柱形散射体形心s=0为x-y坐标轴(笛卡尔直角坐标系)原点，或r-θ坐标系(极坐标系)原点，圆柱散射体s半径为as(s′半径为as′等)，则远场P点相对第s个散射体坐标相应为rs，θs；对第s′个散射体，P点坐标为rs′，θs′；对第s″个散射体坐标为rs″，θs″；以此类推第s′个散射体相对第s个坐标为rss′，θss′。设在不同入射波下 (P波或S波，波数分别为α，β)，入射角为θ0，而平面应变与z轴无关，因此无需考虑剪切波χ。

圆柱体对平面波入射后多重散射的物理过程可表述为：① 任意选择一散射体s为研究对象，该散射体对入射波响应可视为第一重散射；② 第二重散射激发由各散射体第一重散射产生，即第一重散射波可作为次生波源引起第二重乃至更多重散射。考虑散射体s第二重散射计算，所有介质中其它散射体第一重散射可作为第二重散射的次生波源。对所有散射体均遵循此过程，从而获得前一重与后一重散射波函数迭代关系，总散射波场即为所有散射体各重散射的叠加。

1.2 P波或SV波入射

入射P波波场势函数展开成圆柱坐标下Fourier-Bessel级数形式为：

(1)

其中：上标inc表示入射波； Jn(·)为n阶Bessel函数；α，β为P波波数；下标s表示土体；φs=θs+θ0+π/2；为计算方便已消去exp(-iωt) ，φ0。

对弹性桩而言，P波或SV波入射均产生耦合散射，散射波同时存在P波、SV波部分。散射体s位移势函数展开式为：

(2)

透射波势函数参考展开式可表示为：

(3)

涉及P或SV波入射边界条件的应力分量为径向应力与切向应力[13]：

(4)

其中：各变量下标均表示s桩。

第一重散射应满足桩土边界位移与应力连续：

其中：

(6)

(7)

式中：剪切模量G的下标意义同波数。

(8)

其中：上标N’为除桩s外的散射体个数。

第m重散射径向、切向应力表达式为：

(9)

(m-1)重散射应力表达式只需将上式中带m的上下标替换为 (m-1) 即可。透射波第m重透射的径向、切向应力表达式为：

(10)

式中：各符号意义同前，花体符号见附录。

为应用第m重散射边界条件，需对m重散射位移应力波函数进行坐标轴转换，用Graf加法定理转换至与研究对象散射体第s根桩的参考坐标系：

(11)

其中：Hn′n=Hn-n′(·)e-i(n-n′)θss′

将式(1)～式(3)、式(9)～式(11)代入式(8)，得m重散射迭代关系式(见附录式(B))。用Cramer法则将Q矩阵分别代入P矩阵第1～4列得P1，P2，P3，P4矩阵，则m重散(透)射复系数的解为：

(12)

以上迭代关系仍可用假设桩身材料相对土体为刚性进行退化，即Gs/Gp→0，无穷线性方程组式(B)(见附录)可简化成：

(13)

对入射SV波而言，与刚性边界条件推导相同，只需将附录式(A) 等式右边矩阵中入射波项用SV波替代即可，也可令Gs/Gp→0，退化后即为刚性边界条件下的解；而第m重散射与透射系数的求解因其散射波同样含P波、SV波的耦合散射与透射，系数与P波入射所得迭代关系相同，见附录式(B)。

2 算例与分析

相互平行等间距列于介质中截面为圆形桩列见图2(a)。设桩身无限长，桩数N，桩间距sp，屏障总宽度L=(N-1)sp，排间距h。远场稳态平面波垂直传播至该桩列，入射角θ0=π/2。为简化数值计算结果以便分析，Bessel函数展开项截断至n=8。用本文方法计算多排桩隔离效果，采用梅花型布置(图2(b))、排间距为h的双排桩列计算分析。图2(a) 可视为图2(b)排间距h=0的特殊情况，用于验证本文方法的正确性。

数值计算采用桩土剪切模量之比Gr，土体与桩身材料密度比ρr，桩身材料泊松比νp及土体泊松比νs等参数表示波由土体至桩的传播过程一系列特性改变。对所有入射P，S波在土体、桩体频率无量纲化：

(14)

其中：频率η与波长λ右下角标第一个字母代表P或S波入射；第二个字母或波数α，β下角标s或p分别代表土体或桩。

计算用无量纲化位移振幅|u/u0|，|v/v0|，|w/w0|表示总位移振幅与入射波位移振幅比值，且各几何参数均对桩半径无量纲化。各待定系数因波函数展开式级数收敛，数值计算截断至n=8即认为精度满足计算要求。

图2 排桩对平面波散射参考系及分析模型(n=8)

2.1 散射重数影响

图3为单排隔振屏障后中线无量纲位移振幅随散射重数变化曲线，图中：入射P波，sp=3.0as,h=0, 1≤m≤4,N=8)。由图3(a)看出，P波入射、桩土剪切模量比Gr= 1000时，屏障后无量纲位移曲线随散射重数的增加与刚性桩屏障在相同条件下计算结果[10]几乎无异。说明桩土剪切模量比在Gr=1 000左右，屏障可视为刚性，退化结果进一步验证了理论推导的正确性。当散射重数m≥3时，位移振幅增量呈越来越小趋势；散射重数取三重及以上时，三重相对二重、或四重相对三重散射增量绝对值已微乎其微，可认为计算结果收敛，即可将m=4作为散射重数的截断项。

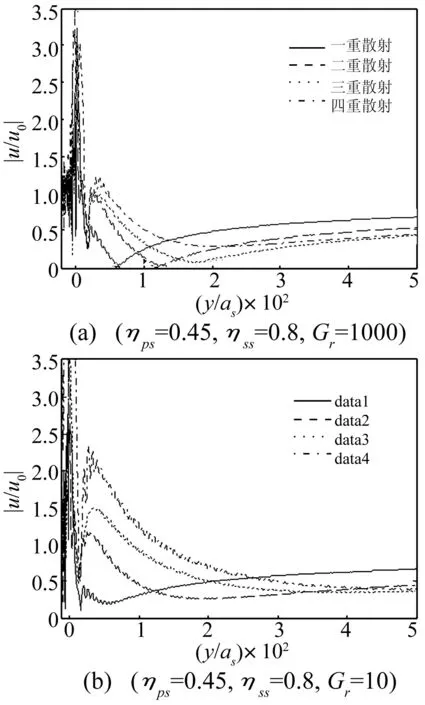
图3 单排隔振屏障后中线无量纲位移振幅随散射重数变化曲线

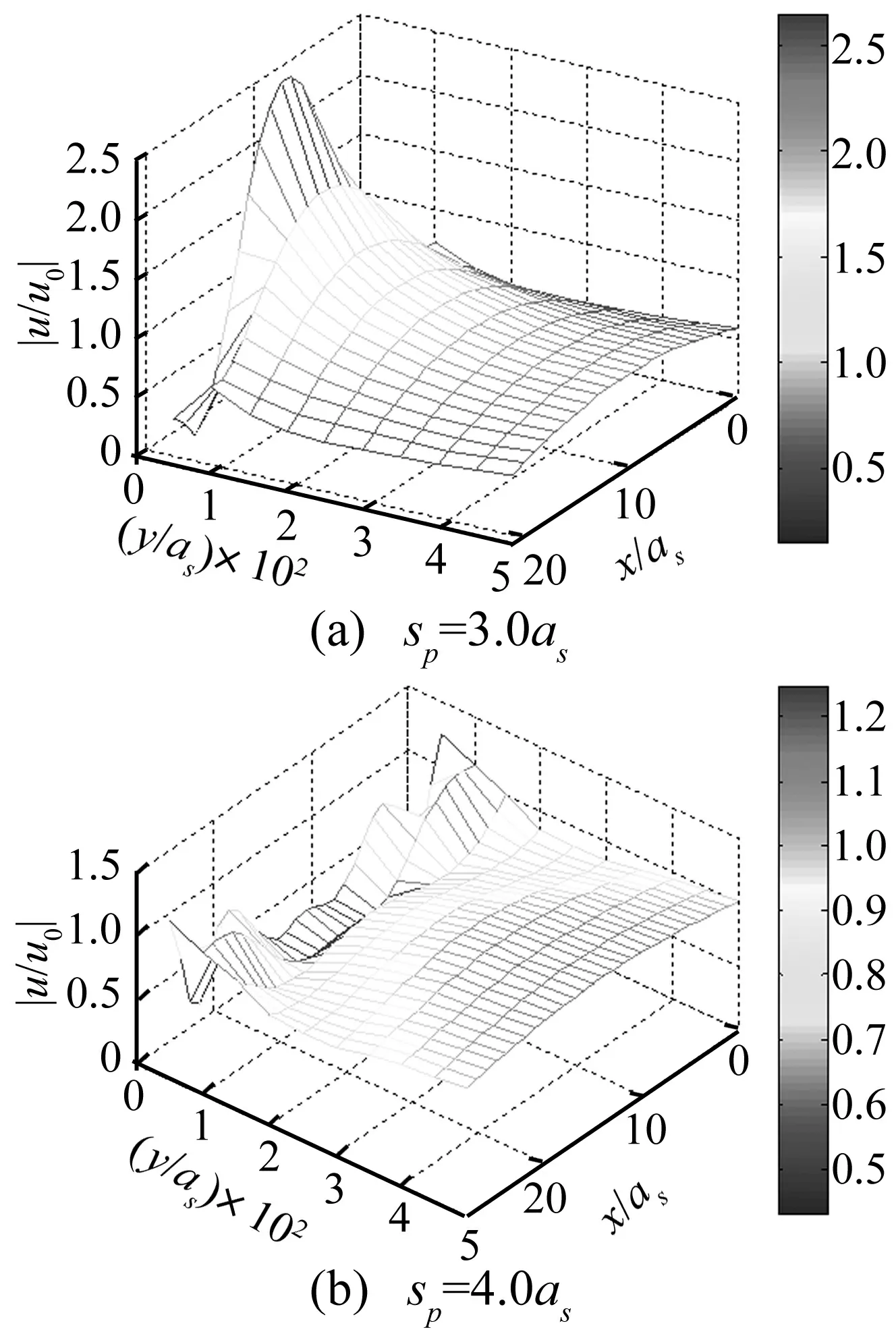
图4 单排桩后无量纲位移振幅随桩间距sp变化三维网格图

2.2 桩间距影响

弹性桩列桩间距为影响屏障隔离效果的重要因素。单排弹性桩(Gr=10)在P波入射下屏障后不同桩间距(sp=3.0as，4.0as)无量纲位移三维网格见图4，图中：h=0,Gr=10,ηps=0.45,ηss=0.8,νp=0.20,νs=0.25,m=4,N=8。图4(a)为P波入射时桩间距在3倍桩径下屏障后无量纲位移振幅的最小值出现在屏障后两侧区域，约0.5左右，图4(b)虽可见靠近屏障处有较小的|u/u0|值，但屏障后其它区域均处在较大|u/u0|范围内，说明随桩间距的增大，类似于连续屏障的排桩体系形成分离个体而不再成为整体对入射波屏蔽。

2.3 排间距影响

多排弹性实心桩排间距亦为影响屏障隔离效果的因素之一。考查P波入射时不同排间距情况屏障后无量纲位移变化见图5，图中：sp=3.0as,ηps=0.45,ηss=0.8,νp= 0.20,νs=0.25,Gr=100,m=4,N=8。由图5(a)、(b)看出，P波入射时排桩后无量纲位移等高线随排间距的变化较敏感，增加一倍桩径间距，使排桩后|u/u0|最小值由0.1升至0.65，且亦能发现屏障后距离较近处振幅放大范围由整块区域逐渐转化为独立于每根桩前的放大区域。说明排桩排间距的加大，即随屏障厚度增加，多排桩逐渐表现出离散、独立的桩列屏障，而不能作为整隔离体对入射波进行屏蔽，只有在保证一定排间距情况下(通常为h/as=3.0)，才能使多排弹性实心桩屏障发挥同连续屏障的隔离效果。

2.4 桩土剪切模量比影响

桩土剪切模量比Gr为弹性桩区别于刚性桩屏障的主要参数之一。在不同桩土剪切模量比情况下屏障后位移振幅等高线见图6，图中：入射P波，sp=3.0as,h=0,ηps=0.45,ηss=0.8,νp=0.20,νs=0.25,m=4,N=8。由图6看出，P波入射时在双排桩屏障后中心区域振幅放大现象明显，最佳隔离区域并非紧靠排桩处，为距排桩一定距离对称分布于桩列两侧位置，弹性桩屏障两侧位移振幅减小量约40%～50%，中心处为30%～40%，直至趋于稳定，而刚性桩位移振幅减小量在两侧能达80%以上，中心亦能屏蔽约70%的入射波。由此看出，随桩土剪切模量比逐渐加大，即桩体逐渐趋于刚性时，排桩屏蔽效果逐渐变好，此与文献[10]等结论一致。而等高线图在Gr=1 000或Gr=+∞时几乎完全相同，说明该弹性桩散射理论退化至刚性假设的合理性及Gr= 1 000时，弹性解可作为刚性解计算，此与刚性边界条件解一致，再次验证本文理论的正确性。

2.5 桩数与排数影响

本文方法与以往计算单排桩屏障区别在于可对任意排列、任意半径的多排桩进行分析。SV波入射下8根双排弹性桩与12根三排弹性桩屏障后无量纲位移振幅等高线对比见图7，图中：sp=3.0as,h=2.5as,ηps=0.45,ηss=0.8,νp=0.20,νs=0.25,Gr=10,m=4。SV波入射时，8根双排弹性桩阻隔后入射波位移振幅靠近中心处减小，可见屏障后两侧存在|v/v0|最小值约为0.2。增加一排桩后，屏障后位移振幅放大现象明显，等高线趋于平均，原在双排桩中心50≤y/as≤100才能获得的|v/v0|=0.4区域在三排桩后大部分范围均能降至该值；最多可隔离90%的入射SV波。说明增加排桩排数可使屏障呈近似连续屏障效果且能获得更理想的减振预期。

图5 隔振屏障后随排间距h变化无量纲位移等高线图

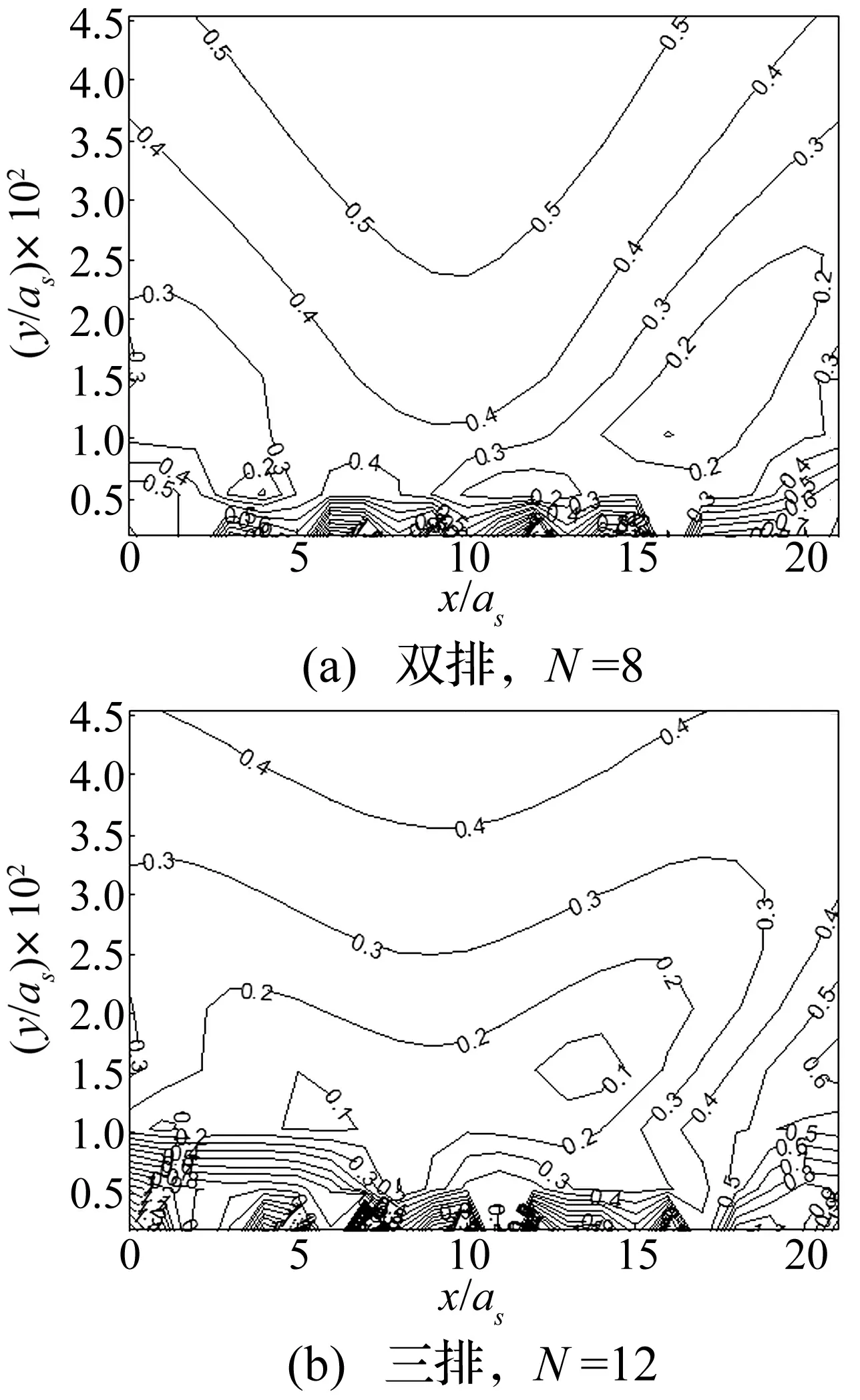
图7 多排桩后无量纲位移振幅等高线图

3 结 论

本文对任意半径、任意布置的圆柱形弹性实心桩隔振屏障对平面弹性波多重散射进行求解。通过施加桩土界面弹性边界条件，构造透射波场函数，采用Graf加法定理对各研究对象进行坐标轴转换并求得第一重散射及透射复系数，通过前一重散射系数可迭代求出后一重散射及透射系数，进而确定最终总散射波场与透射波场。在理论推导基础上数值分析计算讨论影响单排及多排弹性实心桩对平面波隔离效果参数，结论如下：

(1) 平面波入射弹性实心桩屏障后，靠近桩侧会产生位移振幅放大现象，距屏障一定范围(通常y/as≥ 100)位移振幅迅速减小。基于多重散射的弹性屏障计算因考虑桩间互相干涉现象使散射计算更接近实际，并可令非连续屏障得以充分利用。随散射重数的增加位移逐渐收敛，工程上可取4重散射为实际设计截断项。

(2) 弹性实心桩列桩间距及多排桩排间距均对入射平面波散射有较大影响。桩间距与排间距的增加使非连续屏障成为散体，无法保证理想屏蔽作用。通过对屏障后平均无量纲位移振幅等高线分布研究，桩间距与排间距在3.0倍桩半径范围内可获得最优减振效果，并可作为隔振屏障的设计参考指标。

(3) 单排或多排桩身材料与周围介质的剪切模量比为弹性桩区别于刚性桩的重要参数。无论何种平面波入射，随桩土剪切模量比的增加，即桩趋于刚性，屏障后最佳隔离区域逐渐扩大，排桩隔离效果变好。实际工程中多可采用刚性桩为屏障材料。

(4) 增加弹性屏障桩数、排数可明显增强排桩的隔振效果，振幅放大与衰减效应与连续屏障类似。

附录

(A)

其中sθα=ein(θ0+π/2)eiαscos(θ0s+θ0)r0s

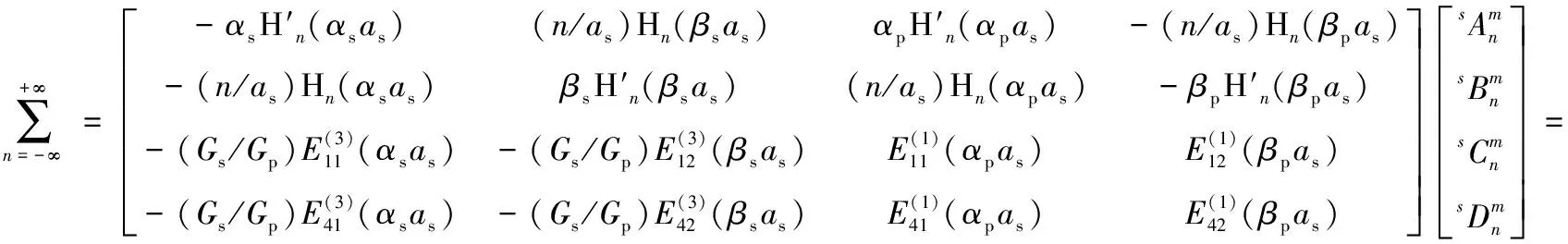
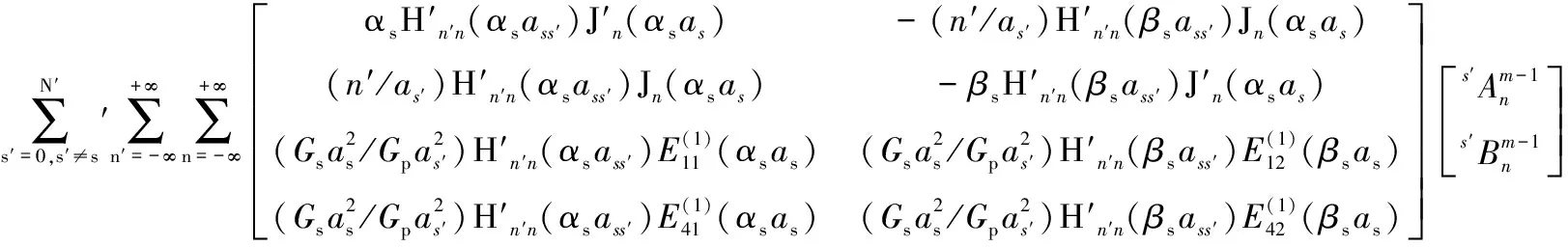
(B)

令：

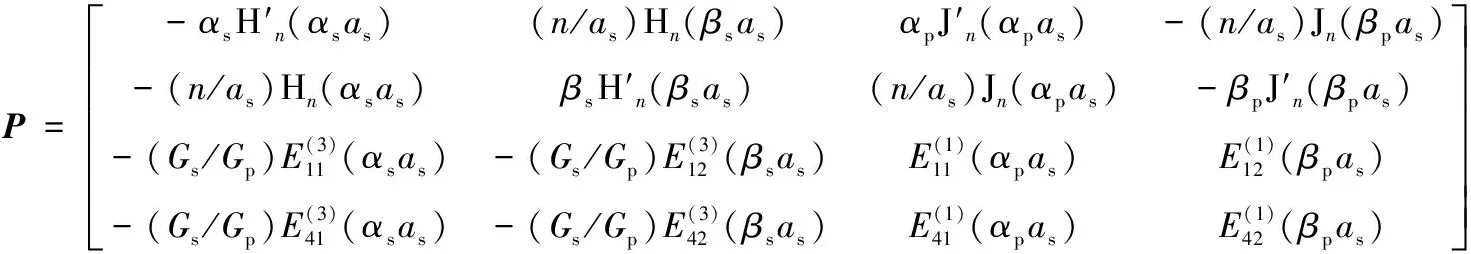
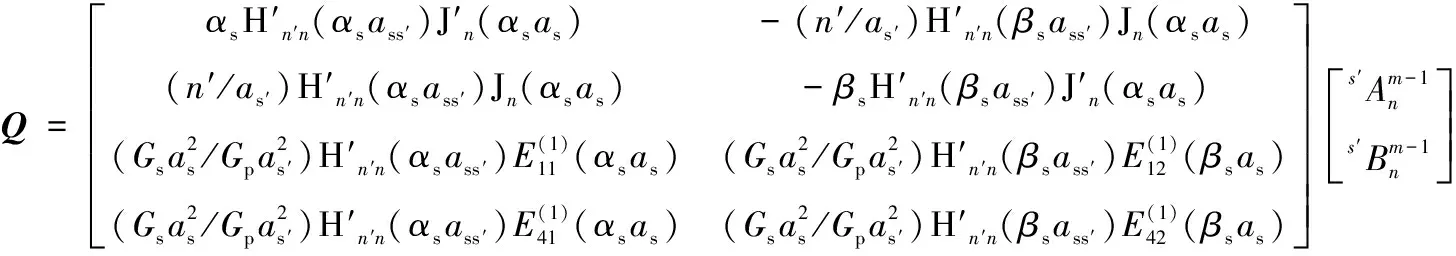
其中：

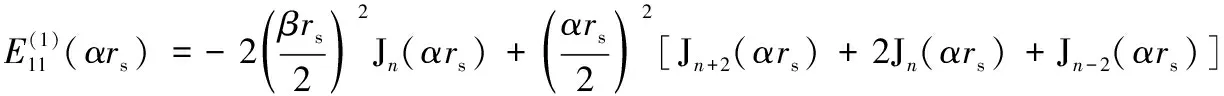
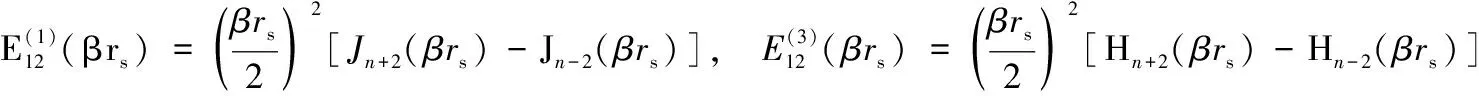
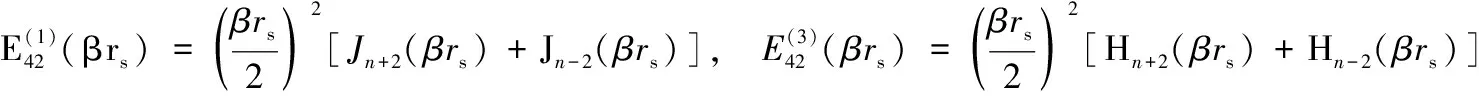
其中:下标α或β可为s或p。

参 考 文 献

[1]Woods R D. Screening of surface waves in soil[J]. Journal of Solids Mechanics and Foundation Division, ASCE, 1968, 94(SM4):951-979.

[2]Liao S, Sangrey D A. Use of piles as isolation barriers[J]. Journal of the Geotechnical Engineering Division, ASCE, 1978,104(9):1139-1152.

[3]Massarsch R, Sanaee F. Vibrationsisolering med hj lp av kalkcementpelare[R]. Internrapport, Avdelingen f r Jord-och Bergmekanik, Kungliga Tekniska Vibrationsisolering mad Hjalp av Kalkeementpelare. Internal Report. Stockholm: Division of Soil and Rock Mechanics, KTH (Royal Inst.Technique.), 1993.

[4]Avil s J, S nchez-sesma F J. Piles as barriers for elastic waves. [J].Journal of Geotechnical Engineering Division, ASCE, 1983, 109(9): 1133-1146.

[5]Avil s J, S nchez-sesma F J. Foundation isolation from vibration using piles as barriers[J]. Journal of Engineering Mechanics,1988, 114(11):1854-1870.

[6]Kattis S E, Polyzos S, Beskos D E. Vibration isolation by a row of piles using a 3-D frequency domain BEM[J]. International Journal of Numerical Methods Engineering,1999,46(5):713-728.

[7]Tsai P H, Feng Z Y, Jen T L. Three-dimensional analysis of the screening effectiveness of hollow pile barriers for foundation-induced vertical vibration[J]. Computers and Geotechnics, 2008,35(3): 489-499.

[8]Cai Y Q, Ding G Y , Xu C J. Screening of plane S waves by an array of rigid piles in poroelastic soil[J]. Journal of Zhejiang University. Science A, 2008,9(5) : 589-599.

[9]Cai Y Q, Ding G Y , Xu C J. Amplitude reduction of elastic waves by a row of piles in poroelastic soil[J]. Computers and Geotechnics, 2009,3(6): 463-473.

[10]Xia T D, Sun M M, Chen C,et al.. Analysis of multiple scattering by an arbitrary configuration of piles as barriers for vibration isolation[J]. Soil Dynamics and Earthquake Engineering, 2011,31(3): 535-545.

[11]夏唐代，孙苗苗，陈 晨．任意排列的弹性实心桩屏障对平面SH波的多重散射[J]. 振动与冲击, 2011，30(7)：87-95.

XIA Tang-dai, SUN Miao-miao, CHEN Chen. Multiple scattering of plane SH wave by an arbitrary configuration of elastic piles as barrier[J]. Journal of Vibration and Shock, 2011,30(7):87-95.

[12]夏唐代,孙苗苗,陈 晨,等.双排刚性桩屏障对平面SH波的隔离性状研究[J].土木建筑与环境工程,2011,33(2):7-11.

XIA Tang-dai, SUN Miao-miao, CHEN Chen,et al.Isolation properties of plane SH wave by double-row rigid pile barriers [J].Journal of Civil,Architectural and Environmental Engineering, 2011,33(2):7-11.

[13]Sancar S, Pao Y H. Spectral analysis of elastic pulses backscattered from two cylindrical cavities in a solid,part I[J]. Journal of the Acoustical Society of America,1981,69(6): 1591-1596.