轨道局部缺陷动态检测冲击特征定位比较法
丁建明, 林建辉,王 晗,易 彩,林 森
(1.西南交通大学 牵引动力国家重点实验室,成都 610031;2. 青岛四方机车车辆股份有限公司 高速列车系统集成国家工程实验室 ,山东 青岛 266111)
近年来,车辆重载化、高速化使轮轨相互作用加强,轮轨接触应力变大。轨道压溃、轨面剥离、轨道波磨、钢轨焊缝等轨道局部缺陷使轮轨相互作用进一步加强,引起轮轨冲击,造成轮轨动态接触应力变大及轮轨系统出现中、高频振动[1],极易导致轨道裂纹萌生、扩展,局部缺陷变大,破坏轨道基础,影响行车安全[2]。轨道局部缺陷超限时的及时更换,将产生昂贵的维修成本并减少路网利用率。解决该问题的根本措施即对轨道进行预防性维修,如钢轨打磨。而轨道预防性维修则需动态检测轨道的技术状态。对此,国内外已有诸多研究,并获得丰硕成果,主要表现在:① 用超声及涡流法检测轨道裂纹,但检测不到轨道局部缺陷[3];② 用测力轮对检测中高频轮轨作用力,利用轮轨力最大值与轨道局部缺陷关联性检测轨道局部缺陷,但涉及的系统复杂,需专门轨检车,高成本不但在支线线路难以广泛,且影响干线使用率[3-4];③ 采用测量轴箱垂向加速度检测轨道的技术状态,由于加速度检测技术成熟、成本低,能直接安装在运营车辆上,受到高度重视。用轴箱垂向加速度二次积分测量轨道不平顺[5],用垂向轴箱加速度判断轨道波磨严重度[4],用有限元分析研究轨道局部缺陷(轨道压溃、轨道焊缝)与振动加速度关系,并用小波提取实测与理论计算加速度信号的小波谱,取得较好的一致性[6],用小波及小波包离线分析轴箱加速度频率与幅值判断评估轨道波磨状态[7]。诸多研究主要分析轨道局部缺陷存在条件下单个轴箱的垂向加速度,以达到认识冲击信号自身本质特征;亦为轨道局部缺陷动态检测奠定了基础。
基于此,本文由多传感融合、冲击特征定位比较角度,提出轨道局部缺陷车载动态检测新方法。利用前后车轮相继冲击轨道局部缺陷特点,对车速积分确定车轮旋转一圈对应的起止时刻,用该时刻截取对应时间历程的前后轴箱垂向加速度,对截取信号作频率切片小波变换提取信号的时频特征,将时频特征的时间轴变换为车轮弧长的位移轴,实现冲击特征车轮圈内定位。在车轮连续旋转三圈内定位特征中,比较前后轴箱加速度能量峰位置,建立轨道局部缺陷动态检测模型实现轨道局部缺陷的动态检测。该方法涉及的系统简单、成本低,方便随车检测。结果表明,该检测方法工程适应性良好,可靠性高,且准确。并通过大量动力学仿真数据验证该方法的有效性,
1 频率切片小波变换基本理论
频率切片小波变换为新的时频分析方法[8],在充分吸收短时傅里叶变换及小波变换优点基础上,通过引入频率切片函数使传统的傅里叶变换实现时频分析功能。能克服短时傅里叶变换频率分辨率固定的缺陷及小波变换依赖小波函数选择的困难以及维格纳分布分析多分量信号存在交叉项干扰的根本缺陷[9],十分适合瞬时冲击、暂态、频率时变的非平稳信号时频特征提取。为此,本文应用频率切片小波变换分析存在轨道局部缺陷车轮轴箱冲击振动的时频特征。
1.1 频率切片小波变换

(1)

通过引入频率平移因子ω实现频率选择函数对应的频率窗在频率轴移动,类似在时间域的短时傅里叶变换。通过引入尺度因子σ实现频率选择函数对应的频率窗伸缩,类似在时间域的小波变换。因此,可通过频率选择函数使传统傅里叶变换实现信号的时频特性分析。
1.2 频率切片函数的特点与选择
应用Parseval原理,将式(1)频率切片小波变换转化到时域描述形式实现,则为:
W(t,ω,λ,σ)=

(2)
式(2)中,即知道频率选择函数的时域表达式,在时间域也不能实现频率切片小波变换。为此需在频率域定义频率选择函数表达式,满足条件为:
(1) 频率选择函数零频率对应幅值非零,即:
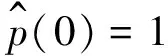
(2) 频率选择函数为有限能量,即:
(3) 频率选择函数为无穷频率的幅值为零,即:

(4) 率选择函数为关于零频率的偶对称函数,即:
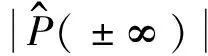
按以上四个条件要求,本文的频率切片频率函数选择为:
1.3 频率切片小波变换尺度因子的确定
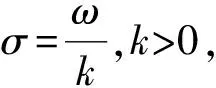
(3)
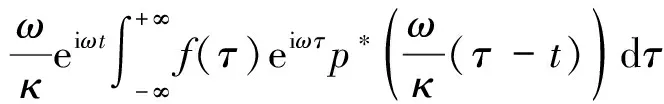
(4)
据Heisenberg不确定原理,不能同时获得到高时间及频率分辨率。为此,需据分析需要对时间分辨及频率分辨率两指标折中考虑。
设频率分辨率比η为:
(5)
式中:Δω为频率变化量。设幅值期望响应比ζ为:
(6)
f(t)=eiωt时,式(6)变为:
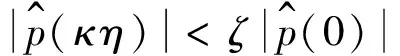
(7)
f(t)=δ(t-t0)时,式(6)变为:
(8)
式中:μ为时间变化量与频率变化量乘积:
μ=ΔωΔt
本文的频率选择函数为高斯函数,故μ=0.5,由式(7)、(8)得不等式组为:
(9)
求解式(9),得:
由此,已实现频率切片小波变换因子的确定,并建立变换因子与时间分辨率、频率分辨关系。
2 轨道局部缺陷动态检测方法与模型
通过速度积分确定截取轴箱加速度的起止时刻,对截取信号做频率切片小波变换,提取前后轴箱加速度冲击特征,通过特征定位与比较实现轨道缺陷的动态检测。
2.1 建立截取前后轴箱加速度时间基准
设车速信号为V(k),k为采样时刻,考虑轴距与车轮周长关系,取车轮旋转三圈对应信号冲击特征进行比较。设时间点4个时刻ki-2,ki-1,ki,ki+1分别对速度积分等于车轮周长,即:
(10)
式中:Sl=2πR,R为车轮半径;S(k)为对应时刻车轮旋转位移。
2.2 提取加速度信号时频特征及特征定位
用4个时刻截取车轮旋转三圈对应三段前后轴箱振动加速度信号:
af,i-1(k)=aq(ki-2∶ki-1)
af,i(k)=aq(ki-1∶ki)
af,i+1(k)=aq(ki∶ki+1)
ah,i-1(k)=ah(ki-2∶ki-1)
ah,i(k)=ah(ki-1∶ki)
ah,i+1(k)=ah(ki∶ki+1)
式中:aq,ah分别为前后轴箱垂向加速度时间历程;ar,i(k),aj,i(k)分别为对应时刻截取前后轴箱加速度。
用式(1)分别对时间基准截取前后轴箱加速度信号做频率切片小波变换,得:
(11)
(12)
以时间为基准点,实现时间与位置的对应,将式(10)分别代入式(11)、(12)得:
(13)
(14)
至此,已实现前后轴箱加速度表征轨道缺陷引起的轮轨冲击特征在圈内的定位。
2.3 建立特征定位的比较规则
计算式(13)分别得前轴箱小波能量峰值对应的车轮圈内旋转位置为Sq,i-1,Sq,i,Sq,i+1;计算式(14)分别得后轴箱小波能量峰值对应的车轮圈内旋转位置为Sh,i-1,Sh,i,Sh,i+1。
规则1为前轴箱能量峰值位移差等于轴距:
ΔSqj=|2πR+Sq,j-Sq,j-1|≤ε,(i-1≤j≤i)
规则2为后轴箱能量峰值位移差等于轴距:
ΔSh,j=|2πR+Sh,j-Sh,j-1-Lt|≤ε,(i-1≤j≤i)
规则3为前后轴箱最高能量位移差等于轴距:
ΔSq,h,j=|2πR+Shm,j-Sqm,j-1-Lt|≤ε,(i-1≤j≤i)
式中:ε为控制误差,本文取0.05 m;Lt为车轮轴距,本文取2.4 m。
如果规则1、2、3同时满足条件,则判断车轮存在局部缺陷。
3 轨道局部缺陷动态检测实例验证
为验证本文所提轨道局部缺陷动态检测冲击特征融合方法的有效性,采用轨道压溃、轨头焊缝凸台的动力学仿真数据对该方法进行验证。建立车辆轨道耦合动力学模型,见图1,包括十自由度车辆模型、九十阶模态轨道模型、轨道压溃输入模型、非线性赫兹接触轮轨耦合模型[10]。由于主要分析轨道局部缺陷的动力作用,该动力学模型未考虑轨枕及道床部分。用翟方法[11]计算耦合动力学模型。

图1 车辆轨道耦合动力学模型
3.1 十自由度车辆动力学模型
车辆动力学模型包括车体、前后构架及其沉浮、点头、4轮对沉浮运动,振动微分方程为:

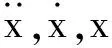
3.2 九十阶模态轨道动力学模型
轨道模型采用连续支撑的欧拉梁力学模型,振动微分方程为:
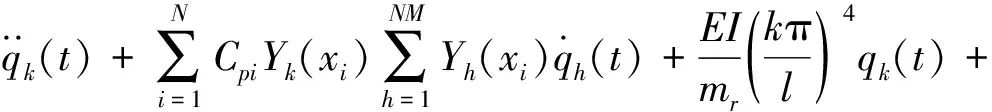
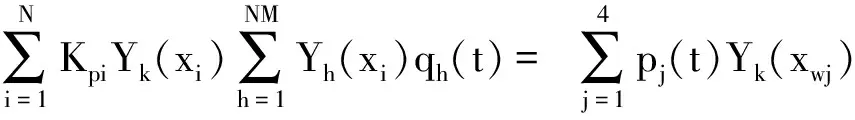
式中:q1(t),q2(t),q3(t),q4(t)分别为第一、二、三、四轮对对应的轮轨接触力;Cpi为扣件阻尼;Kpi为扣件刚度;N为离散支撑数量;NM为分析轨道模态阶数;qh(t)为钢轨正则振型坐标;Yh(xi)为钢轨振型;E,I,l分别为轨道弹性模量、截面转动惯量、轨道长度;mr为钢轨线密度。
轨道垂向振动位移为:
3.3 轨道局部缺陷的输入模型
以单一谐波模拟轨道局部压溃模型及焊缝、凸台模型,采用位移输入法建立轨道压溃输入模型:
式中:x为纵向位移;ζ(x)为缺陷对应的轨道高低不平顺;L为缺陷长度;a为缺陷深度。
该模型不仅描述出缺陷的几何形态,且能反映轮轨冲击的高频特性。为轨道局部缺陷检测提供了可能。将轨道缺陷不平顺模型与深圳地铁轨道线路实测不平顺zg0(x)进行叠加作为新的轨道不平顺输入,实现轨道缺陷输入:
z0(x,t)=zg0(x,t)+ζ(x,t)
3.4 轮轨非线性赫兹接触模型
第j轮对轮轨垂向压缩量L(x,t)为:
Lj(x,t)=Zwj(t)-Zrj(t)-z0(x,t)
用Hertz非线性接触理论计算轮轨力为:
Lj(x,t)>0时
Lj(x,t)≤0时
pj(t)=0
式中:G=3.86R-0.115×10-8为轮轨接触参数。
3.5 不同轨道缺陷尺寸与速度下算法测试
车辆以时速70 km、90 km、110 km、130 km、150 km分别通过①缺陷长度L=20 mm,缺陷深度a=0.4 mm;②缺陷长度L=40 mm,缺陷深度a=0.4 mm两种尺寸轨道缺陷进行动力学仿真,计算获得前后轴箱垂向加速度响应时间历程数据。用本文所提轨道局部缺陷动态检测模型及方法处理10种工况数据。以70 km通过缺陷长度L=20 mm的垂向振动响应加速度信号见图2,信号长度为车轮旋转三圈获得。
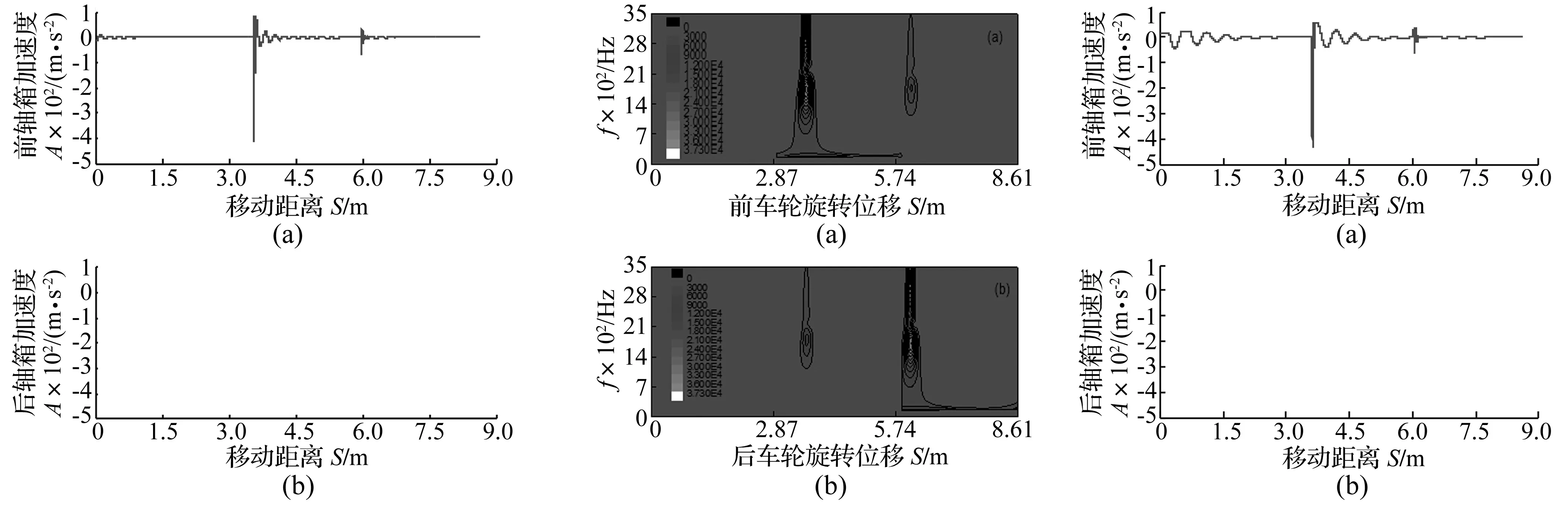
图2 轴箱垂向加速度
采用本文所提轨道局部缺陷动态检测方法与模型中时频特征及特征融合方法对该数据分析处理,结果见图3。由图3(a)、(b)对比可知,前后车轮第一圈内(位移0~2.87 m)冲击能量较小;车轮第二圈内(位移2.87~5.74 m)前车轮遇到轨道缺陷的冲击能量较大,后车轮冲击能量较小。原因为前车轮振动通过构架传递到后车轮;车轮旋转的第三圈(位移5.74~8.61 m),后车轮经轨道缺陷而冲击能量较大,前车轮因后车轮振动通过构架传递而振动能量较小,前后轴箱最大能量峰值对应的移动距离位于车轮轴距约2.4 m(本文所用轴距仿真参数为2.4 m)。说明本文所提出方法能揭示车辆前后车轮相继冲击轨道缺陷的冲击过程,为轨道局部缺陷动态车载动态检测提供有力信号特征。
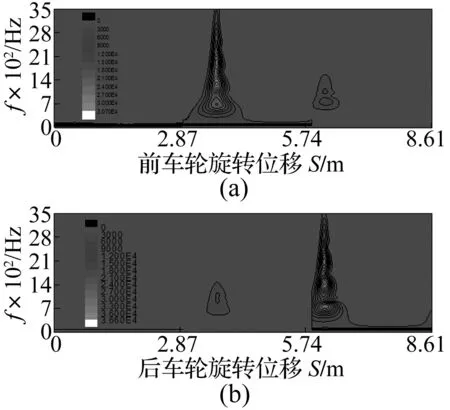
图5 前后轴箱加速度的时频特征
以150 km通过缺陷长度L=40 mm的振动响应加速度信号见图4。采用本文所提方法对该数据分析处理,结果见图5。
比较图3可得与图5一致的结论。对仿真计算其它工况时频分析不再详述。将20种仿真数据用本文方法及模型进行处理,分别得车轮旋转一周能量峰值位置、前后峰值对应位置差、前后轴箱最大能量位置差、判断结果,见表1、表2。
需要说明的是前轴箱最大能量峰对应位置在第二圈,后轴箱最大能量峰对应位置在第三圈。由表1、表2看出,本文方法及模型能可靠、准确检测轨道局部缺陷,从而验证所提方法的有效性。
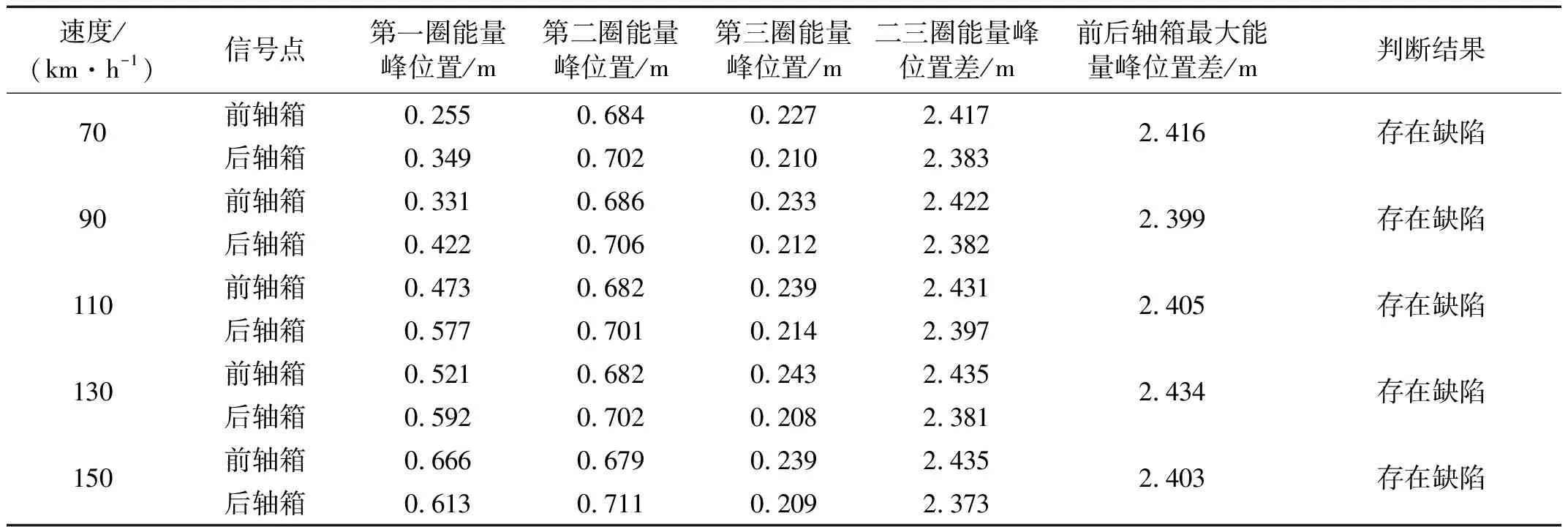
表1 缺陷长度L=20 mm算法验证结果
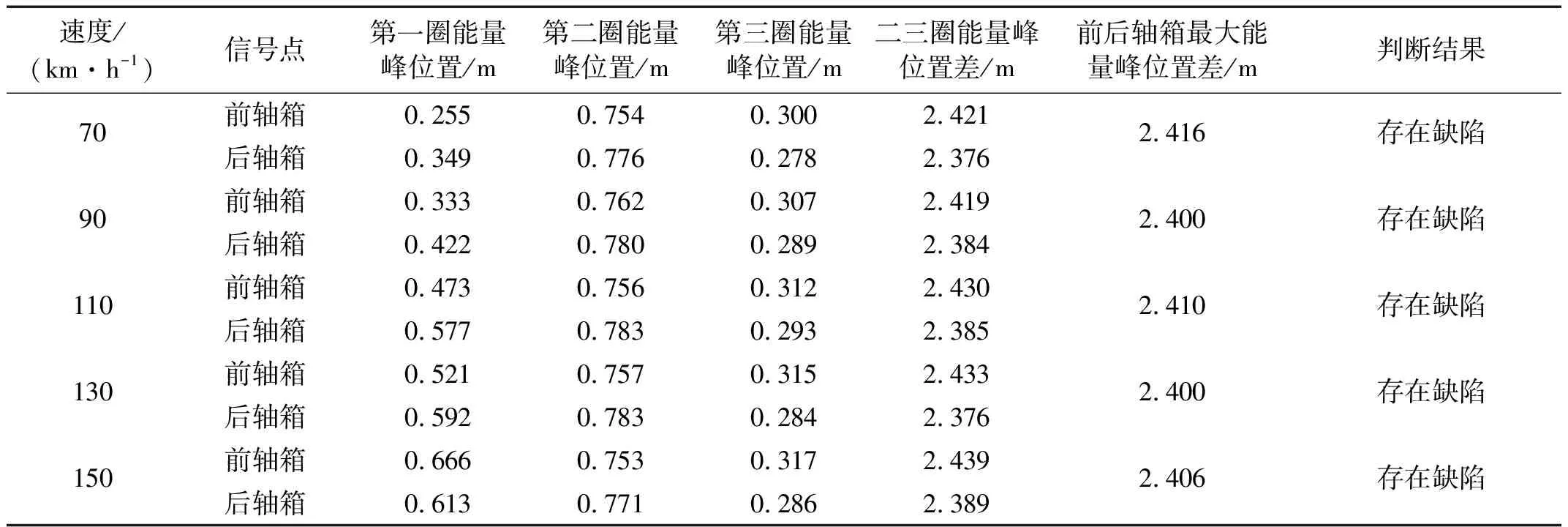
表2 缺陷长度L=40 mm的算法验证结果
4 结 论
本文将现代信号处理频率切片的小波变换与车辆对象特性、前后车轮相继冲击同一轨道缺陷的振动特性相结合,提出的轨道局部缺陷动态检测车载检测方法,结论如下:
(1) 充分利用频率切片小波变换揭示冲击信号时频特征的独特优势,在小波变换域用车速信号实现车轮冲击轨道局部缺陷的冲击特征峰值能量定位;
(2) 该车载检测方法充分考虑车辆对象特性,用冲击能量定位与轴距比较判断轨道缺陷。将车辆对象特性与冲击特性融合方法也可用于钢轨剥离、波浪形磨耗的轨道短波检测及车轮缺陷车载检测;
(3) 轨道局部缺陷检测方法涉及的系统简单、可靠、成本低廉,具有一定工程应用前景。亦为进一步研究轨道局部缺陷严重度评价奠定基础。
参 考 文 献
[1]Molodova M,Li Z L, Dollevoet R. Axle box acceleration: measurement and simulation for detection of short track defect[J]. Wear, 2011, 271(1-2): 349-356.
[2]Caprioli A, Cigada A, Raveglia D. Rail inspection in track maintenance: a benchmark between the wavelet approach and more conventional Fourier analysis[J]. Machanical Systems and Signal Processing, 2007,21(2):631-652.
[3]Guller P, Andersson L, Lunden R. High-frequency vertical wheel-rail contact forces-field measure-ments and influence of track irregularities[J]. Wear, 2008,265(9-10):1472-1478.
[4]Kojima T, Tsunashima H, Matsumoto A. Fault detection of railway track by multi-resolution analysis[J].Computer in Railways,2006(88):955-964.
[5]Weston P F, Ling C S, Robert C,et al. Monitoring vertical track irregularity from in-service railway vehicles[J].Proceedings of the institution of mechanical engineers, part F[J].Journal of Rail and Rapid Transit,2007,211(1):75-88.
[6]Li Z L, Zhao X, Esveld C,et al. An investigation into the causes of squats-correlation analysis and numerical modeling[J]. Wear, 2008,265(9-10): 1349-1355.
[7]Gomes R, Batista A, Ortigueira M. A tool for the detection and quantification of rail corrugation[J]. IFIP AICT, 2010,314:401-408.
[8]Yan Z, Miyamoto A, Jiang Z. Frequency slice wavelet transform for transient vibration response analysis[J].Mechanical system and signal processing,2009,23(5):1474-1489.
[9]段晨东,高 强. 基于时频切片分析的故障诊断方法及应用[J].振动与冲击,2011,30(9):1-5.
[10]DUAN Chen-dong, GAO Qiang. Novel fault diagnosis approachs using time-frequency slice analysis and its application[J].Journal of Vibration and Shock,2011,30(9):1-5.
[11]翟婉明. 车辆-轨道耦合动力学(第三版)[M].北京:科学出版社,2007.
[12]ZHAI Wan-ming. Two simple fast integration methods for large-scale dynaminc problems in engineering[J]. International Journal for Numerical Methods in Engineering, 1996, 39(24):4199-4214.

