一种判断LR分解是否存在的优化算法

沈家铭

(四川大学 数学学院， 四川 成都 610065)

一种判断LR分解是否存在的优化算法

沈家铭

(四川大学 数学学院， 四川 成都 610065)

使用定理直接判断方阵A是否存在LR分解的计算难度系数为O(n3)，文中在此基础上提出了一个改进算法,将计算难度降为O(n2)。给出了设计思路及推导方法，并用Matlab实现了两种算法，通过例题验证了计算效率的提升。

LR分解; 方阵; 算法; Matlab

0 引 言

在有应用背景的数学问题中，很多求解问题最终都可归结为线性方程组的求解。因此，解线性方程组在科学与工程计算中有着十分重要的作用。对其系数矩阵进行三角分解，是一种解线性方程组的有效方法，LR分解是求三角分解的一个强有力的算法,受到了人们的极大关注。在不进行行列置换的前提下，为了判断方阵A的LR分解是否存在，是进行LR分解的前提[1-4]。文中给出了一种快速判断方阵LR分解是否存在，同时计算LR分解的算法,大大提升了计算速度。

1 问题描述

定义：LR分解：

即把矩阵A分解为一个下三角矩阵L和一个上三角矩阵R

而如何求证方阵A是否存在唯一的LR分解，有以下定理:

定理1 设A为n阶方阵，A的k阶主子式记为

则A的LR分解存在唯一的充分必要条件是

记

2 计算方法

为此，需要计算n-1个矩阵行列式的值。而容易证明，矩阵行列式的值就等于矩阵LR分解得到的R矩阵的对角元的乘积。

同时， d1≠0时可以得到A2的LR分解存在，由此算得d2，而若d2≠0，又已知d1≠0，所以A3的LR分解存在，以此类推，可以得到dk(k=1,2,…,n-1)的值。

由这个思路，可以得到算法1的计算步骤如下：

1)对Ak用Doolittle算法做LR分解；

2)由U计算dk；

3)若dk≠0，则k=k+1，否则返回错误，不能进行LR分解。按此思路即可得到算法1的Matlab程序代码如下：

function[L,R,pp] =LR_P(A)

tic;

[n,m]=size(A);

R=zeros(n);

L=eye(n);

suM=0;

R(1,1)=A(1,1);

pan=R(1,1);

pp=0;

ifpan==0;

pp=-1;

return

end

fori=2:n;

forj=1:i-1;

fork=1:j-1

suM=suM+L(j,k)*R(k,i);

end

R(j,i)=A(j,i)-suM;

suM=0;

fork=1:j-1

suM=suM+R(k,j)*L(i,k);

end

L(i,j)=(A(i,j)-suM)/R(j,j);

end

R(i,i)=A(i,i)-L(i,1:i-1)*R(1:i-1,i);

pan=pan*R(i,i);

ifpan==0&&i～=n;

pp=-1;

return;

end

end

toc;

end

Doolittle分解算法代码:

function[L,R]=LR_L(A)

[n,m]=size(A);

R=zeros(n);

L=eye(n);suM=0;

R(1,1)=A(1,1);

fori=2:n;

forj=1:i-1;

fork=1:j-1

suM=suM+L(j,k)*R(k,i);

end

R(j,i)=A(j,i)-suM;

suM=0;

fork=1:j-1

suM=suM+R(k,j)*L(i,k);

end

L(i,j)=(A(i,j)-suM)/R(j,j);

end

R(i,i)=A(i,i)-L(i,1:i-1)*R(1:i-1,i);

end

end

3 计算方法的改进

n次LR分解的计算量非常大，是一个十分耗费时间的过程，其时间难度为O(n3)，为此，寻找是否有优化算法使得计算量减少[5-7]。

通过上述算法可以知道，每次LR分解的矩阵之间是有联系的。它们之间的关系是：前一个矩阵增加一行一列就是后一个矩阵[8]，故进行尝试，已知矩阵A的LR分解式，是否能通过LR计算在末尾增加一行一列的矩阵A*的LR分解式L*，R*。

3.1改进算法的推导

设矩阵A的LR分解式已知，不妨设增加一行一列以后的矩阵为：

其中

使用待定系数法，设

其中

则有

所以

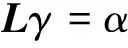
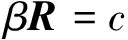
即

可解得

然后可以得到

则通过A的LR分解式得到了在末尾添加一行一列A′的LR分解式A′=L′R′。

通过这种算法，使得在判断A是否存在LR分解式，以及同时计算A分解式的LR的时间难度从O(n3)变为了O(n2)。

观察解出来的β,γ的形式可以发现，每次对A加一行一列以后做LR分解，并不影响之前的分解结果，而且在算β,γ的时候推出来的递推公式与Doolittle算法中对LR分解的算法递推公式形式几乎一致。通过比较得出了以下结论:改进的算法(以上)与原算法区别只是计算的次序不同。

改进的算法是从主对角元开始，一圈一圈向外计算，也就是说a11开始，计算r11,然后计算r11周边的元素r12,r22,l21,…。

每算完一圈，利用∏rii是否为0判断能否进行LR分解，若进行到某一步时，该式为0，则该矩阵不能进行LR分解，反之，则可以。

3.2改进算法的实现

我们得到如下改进的LR分解算法,称之为算法2：

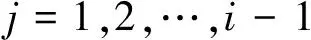
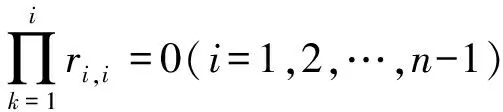
算法2的Matlab代码如下：

function [L,R,pp] = LR_P2(A)

tic;

p=1;

[n,～]=size(A);

for i=1:n

if p==0

pp=-1;

break;

end

p=1;

A_=A(1:i,1:i);

[L,R]=LR_L(A_);//Dolittle算法，for j=1:i

p=p*R(i,i);

end

pp=0;

toc;

end

end

4 计算效率验证

使用算法1和算法2的代码做了一个简单的例题来验证计算，检验计算速度是否有提高。

对一个1 024×1 024的矩阵进行LR分解，矩阵来源是一张1 024×768的点阵图片。

在平台为intel 2640qm,内存8 GB，Matlab环境下，统一计算平台下对1 024×1 024的矩阵用两个算法进行对比。

算法1：Elapsed time is 2 331 seconds。

算法2：Elapsed time is 12 seconds。

可见效率提升了194.25倍。

5 结 语

在定理的基础上设计实现了一种高效的判断LR分解是否存在以及计算LR分解式的算法。算例测试证明了算法可行性和效率的提高。

[1] 高惠璇.统计计算[M].北京：北京大学出版社,1997.

[2] 徐晓飞,曹祥玉,姚旭,等.一种基于Doolittle LU分解的线性方程组并行求解方法[J].电子与信息学报,2010(8):2019-2022.

[3] G H Golub. Matrix computation 4th edition[M].北京：人民邮电出版社,2014.

[4] 王群英.矩阵分解方法的探究[J].长春工业大学学报:自然科学版，2011，32(1):95-101.

[5] 戴华.矩阵论[M].北京：科学出版社，2001：110-145.

[6] 徐泰燕，郝玉龙.非负矩阵分解及其应用现状分析[J].武汉工业学院学报，2010(1):110-115.

[7] 黄丽嫦.矩阵的LU并行递归分解算法的设计研究[J].科学技术与工程，2012(5)：3626-3629.

[8] 周康，陈金.基于部分基变量的LP问题矩阵算法[J].运筹学学报，2012(6)：121-126.

AnoptimizationalgorithmtodeterminetheexistenceofLRdecomposition

SHENJia-ming

(SchoolofMathematics,SichuanUniversity,Chengdu610065,China)

SincethecalculatingdifficultycoefficientofLRdecompositionisO(n3),byusingthetheoremtojudgewhetherphalanxAexists,hereweputforwardanimprovedalgorithmtoreducethecalculatingdifficultycoefficienttoO(n2).Designandderivationmethodaregiven,andtwoalgorithmsareimplementedwithmatlab.Thecalculationefficiencyimprovementisverifiedwithexamples.

LRdecomposition;phalanx;algorithm;Matlab.

2014-07-18

沈家铭(1993-)，男，汉族，云南昆明人，主要从事统计计算方向研究,E-mail:493879714@qq.com.

O 151.21

A

1674-1374(2014)05-0593-04