Kuramato-Tsuzuki方程的有限差分法

周 丽

(安徽农业大学 数学系， 安徽 合肥 230031)

Kuramato-Tsuzuki方程的有限差分法

周 丽

(安徽农业大学 数学系， 安徽 合肥 230031)

对二维Kuramoto-Tsuzuki方程混合初边值问题建立了线性化Grank-Nicolson格式，证明了差分格式解存在的唯一性、收敛性，并证明了收敛阶为O(τ+h2)。

Kuramoto-Tsuzuki方程; 差分格式; 收敛性

0 引 言

Kuramoto-Tsuzuki方程描述了在歧点附近两个分支的行为状况[1]，文中讨论混合初边值问题的Kuramoto-Tsuzuki方程[2]的数值解

(1)

(2)

(3)

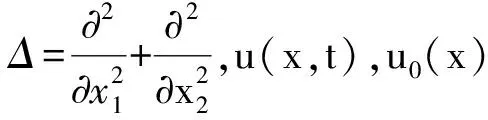
1 差分格式的建立

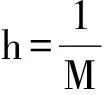
对方程(1)-方程(3)建立如下线性化Grank-Nicolson格式：

(4)

(5)

2 差分格式的可解性和收敛性

首先引入下面的Brouwer不动点定理[8-9]:引理1 设(H,(·,·)H)是有限维内积空间，‖·‖H是其上定义的范数，映射g:H→H是连续的，若存在α>0,使得对任意z∈H,‖z‖H=α，有Re(g(z),z)H≥0成立，则存在z*∈H,使得‖z*‖≤α时g(z*)=0。

证明 将方程(4)改写成:

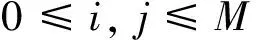
做映射G:CM+1→CM+1

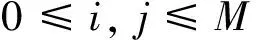
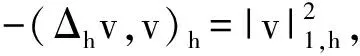
对上式两边同时取实部得

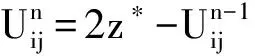
解的唯一性用数学归纳法可证，证明略。

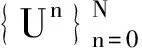
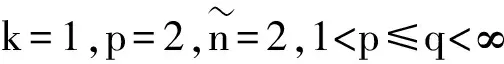
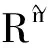
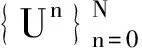
证明 由于

其中

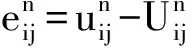
(6)

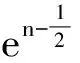
(7)

假设u(x,t)在Ω×(0，T]上有界，则

由引理3知

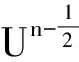
由引理3

两边同时取实部得

当τ充分小时，由离散Gronwall不等式得到

命题得证。

[1]YKuramoto，TTsuzuki.Ontheformationofdissipativestructiveinreaction-diffusionsystems[J].ProgrTheorPhys.,1975,54:689-699.

[2] Tingchun Wang, Boling Guo. A robust semi-explicit difference scheme for the Kuramoto-Tsuzuki equation [J]. J.Compu-tational and Applied Mathematics,2009,233:878-888.

[3] Z Z Sun. A linearized difference for the Kuramato-Tsuzuki equation [J]. Comput Math.,1996,14:1-7.

[4] Z Z Sun. OnL∞convergence of a linearized difference scheme for the Kuramato-Tsuzuki equation [J]. Nanjing Univ. J.Math. Biquarterly.，1997,14(1):5-9.

[5] Z Z Sun. A generalized Box scheme for the Kuramato-Tsuzuki equation[J]. J.Southeast Univ.，1996,26(1):87-92.

[6] G Z Tsertsvadze. On tne convergence of a linearized difference scheme for the Kuramato-Tsuzuki equation and for systems of reaction-diffusion type[J]. Zh Vychisl Mat. Fiz.,1991,31:698-707.

[7] Z Z Sun, Q D Zhu. On tsertsvadze’s difference scheme for the Kuramato-Tsuzuki equation[J]. J.Comp., Appl., Math.,1998,98:289-304.

[8] G D Akrivis. Finite difference discretization of the cubic schrodinger equation[J]. IMA J.Numer Anal.,1993,13:115-124.

[9] G D Akrivis, V A Dougalis, O A Karakashian. On fully discrete galerkin methods of second-order temporal accu-racy for the nonlinear schrodinger equation[J]. Numer Math.,1991,59:31-53.

A finite difference scheme for Kuramoto-Tsuzuk equation

ZHOU Li

(Department of Mathematics, Anhui Agricultural University, Hefei 230031， China)

A linearized Crank-Nicolson finite difference scheme is studied for the mixed initial boundary of two-dimensional Kuramoto-Tsuzuki equations. Existence, uniqueness of the solutions are proved and the convergence order isO(τ+h2).

Kuramoto-Tsuzuki equation; difference scheme; convergence.

2014-06-02

安徽农业大学青年科学基金资助项目(2011zr007)

周 丽(1981-)，女，汉族，安徽蚌埠人，安徽农业大学讲师，硕士，主要从事偏微分方程的数值解方向研究,E-mail:lizhou@ahau.edu.cn.

O 241.82

A

1674-1374(2014)05-0585-04