同心圆亚像素中心定位方法

张方程, 李晓天

(中国科学院长春光学精密机械与物理研究所， 吉林 长春 130033)

同心圆亚像素中心定位方法

张方程, 李晓天

(中国科学院长春光学精密机械与物理研究所， 吉林 长春 130033)

基于椭圆曲线拟合和曲率滤波,提出同心圆投影中心定位方法。采用单应矩阵变换和坐标平移法生成了大量的理想测试图像，并与角点检测法的测量精度进行了比较，结果表明，文中方法的测量精度在有无噪声情况下均高于角点检测方法。当信噪比介于35 dB和25 dB之间时，角点检测法的测量误差突然急剧增大，文中方法的测量误差变化仍比较平缓，测量误差小于0.15 pixel。

机器视觉； 图像处理； 同心圆定标； 椭圆拟合

0 引 言

平面同心圆的投影中心可用作对摄像机进行内外参数标定，弥补角点检测法和圆心法的定位不准确问题。一个圆的投影圆心与其在图像中的椭圆中心不具备仿射不变对应关系[1-3]，因此采用图像椭圆中心来代替投影圆心的成像坐标方法将带来一定的定位误差。根据小孔成像和仿射变换原理，平面内同心圆在经过摄像机拍摄后的数字图像中表现形式为两个中心分离的椭圆，当且仅当摄像机光轴与同心圆所在平面严格垂直时，同心圆所成的像为两个中心重合的圆。2001年Kim和Kweon[1]指出，按照仿射变换原理，平面同心圆的投影中心与两个成像椭圆中心共线，并提出采用交比不变的方法对同心圆的投影中心进行定位。随后，Xianghua Ying[4],Jun-Sik Kim[2],Ashutosh Morde[3],Jun Peng Xue[5]等学者对同心圆投影中心定位方法进行了研究，但主要围绕采用不同几何点进行仿射不变方法实现同心圆投影中心定位及其在摄像机定标中的应用进行探讨，没有对同心圆的投影中心的提取方法及其提取精度进行分析。

文中提出采用经过曲率滤波的曲线拟合方法来实现同心圆投影中心的亚像素定位。首先提取两椭圆边界的亚像素定位坐标，并采用曲率滤波方法剔除掉误差较大的椭圆边界点对两个椭圆方程进行最小二乘法拟合。然后根据两个椭圆中心亚像素级坐标以及两个椭圆的方程，采用仿射变换方法对同心圆的投影中心进行定位和逼近。最后在有无噪声的情况下对文中方法和角点检测法[6]的图像点提取精度进行对比仿真分析，并给出了实验测量结果。

1 数学建模

1.1图像预处理

摄像机采集到的图像存在着大量的噪声，因此在进行边缘检测前要先对图像进行平滑去噪处理。这里采用的是具有一定的边缘保持功能的二维高斯滤波器

(1)

然后通过阈值化方法对投影同心圆质心进行粗定位,并提取出包含同心圆的感兴趣区域(ROI)，后续的计算只对该区域所包含的256色灰度图像进行操作，如图1所示。

1.2双线性插值与椭圆边缘的粗定位

根据方形孔径原理，由于光学元器件的卷积以及衍射作用，图像边缘灰度值变换表征为高斯分布，高斯曲线的顶点对应的位置即为真实边缘点的位置。为提高计算速度，文中采用一维高斯边缘检测的方法对椭圆边缘进行粗定位。首先通过质心(xg，yg)的θ角在0到 π之间的各条直线所对应的像素坐标进行邻近点双线性插值，然后提取一维亚像素级高斯边缘，从而获得两个椭圆的边缘点图像坐标。

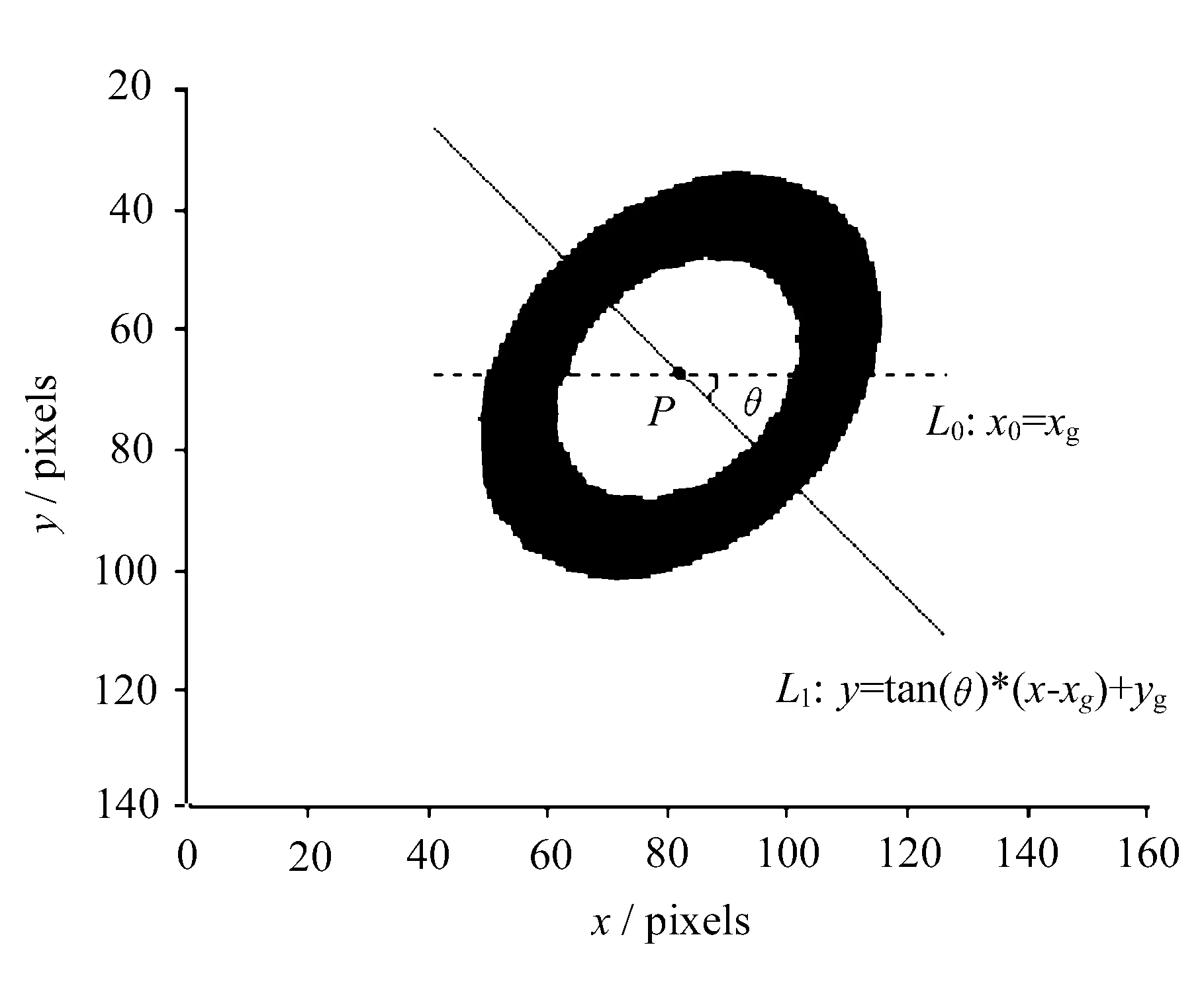
图1 ROI图像的像素级边缘提取

1.2.1 双线性插值

在进行双线性插值前，要先将直线L1离散化，此时要根据L1斜率的不同，而选择不同的离散方法。当|tanθ|≤1时，令x在直线L1被图1所包含的范围内以1个像素等间隔进行递增变化，根据直线L1方程对相应的y值进行求解；当|tanθ|>1时，令y在直线L1被图1所包含的范围内以1个像素等间隔进行递增变化，根据直线L1方程对相应的x值进行求解。

双线性插值方法认为图像的灰度在横向和纵向方向上都是线性变化的，这与光学成像的渐变原理相一致[6-8]。设直线L1上任一点P的坐标为(xp,yp)，若xp和yp皆为整数，则P点的灰度值IP可直接从同心圆图像中读取，记为I(xp,yp)。若xp和yp不全为整数，则P点的双线性插值灰度值IP为:

(2)

式中:a,b----分别与xp,yp最近整数;

I(a,b),I(a+1,b),I(a,b+1)，I(a+1,b+1)----分别为对应的整数点坐标的灰度值。

1.2.2 一阶高斯离散变换

设离散高斯变换的长度f为奇数，则离散的高斯函数一阶导数的表达式为

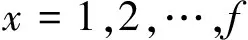
(3)

沿着直线L1的方向对图像进行双线性插值并获得一维图像数据后,采用离散的高斯函数一阶导数对一维图像灰度数据进行卷积运算，可获得曲线如图2所示。

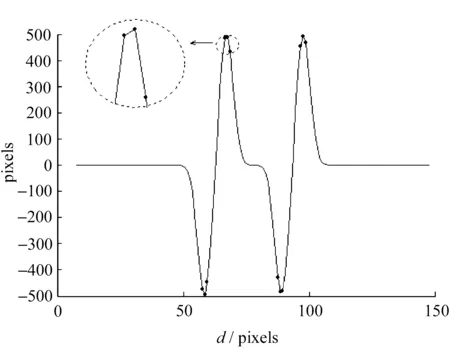
图2 ROI图像某θ角方向的一维一阶高斯变换曲线

由于图2曲线峰值附近各点呈一维高斯分布，而对一维高斯函数的等式两端取自然对数，获得的新函数变换规律符合抛物线方程，因此,可根据曲线顶点附近3点的灰度差值(M轴的坐标值)的自然对数求得抛物线的顶点，该点所对应的图像位置即为边缘点亚像素级位置。

由图2中的虚线圆所包含的顶峰上的顶点坐标(d0,M0)以及其左右两点坐标(d0-1,ML)和(d0+1,MR)，对抛物线顶点坐标进行计算，求得边缘点的坐标为

(4)

将d0sub根据tan(θ)的取值不同，代入到直线L1的方程中，即可获得亚像素级边缘点的坐标。

1.3曲率滤波

由于图像中噪声的存在，使得少部分边缘点的计算位置与实际位置存在较大偏差。因此,在进行椭圆方程曲线拟合前，需将这些计算误差较大的边缘点过滤掉，否则将影响椭圆方程的拟合精度。

设(x1,y1),(x2,y2),(x3,y3)为椭圆边缘上的任意连续3点，则(x2,y2)点处的曲率kr计算公式为

(5)

其中

根据椭圆方程可知，椭圆的曲率在长轴的端点处取最大值，在短轴端点处取最小值，曲率变化呈渐变趋势，因此可根据式(5)将曲率值发生突变的边缘点过滤掉。文中对经过边缘检测的两椭圆的边缘点加入了噪声，进行曲率滤波前后的边缘点曲率变化曲线分别如图3和图4所示。

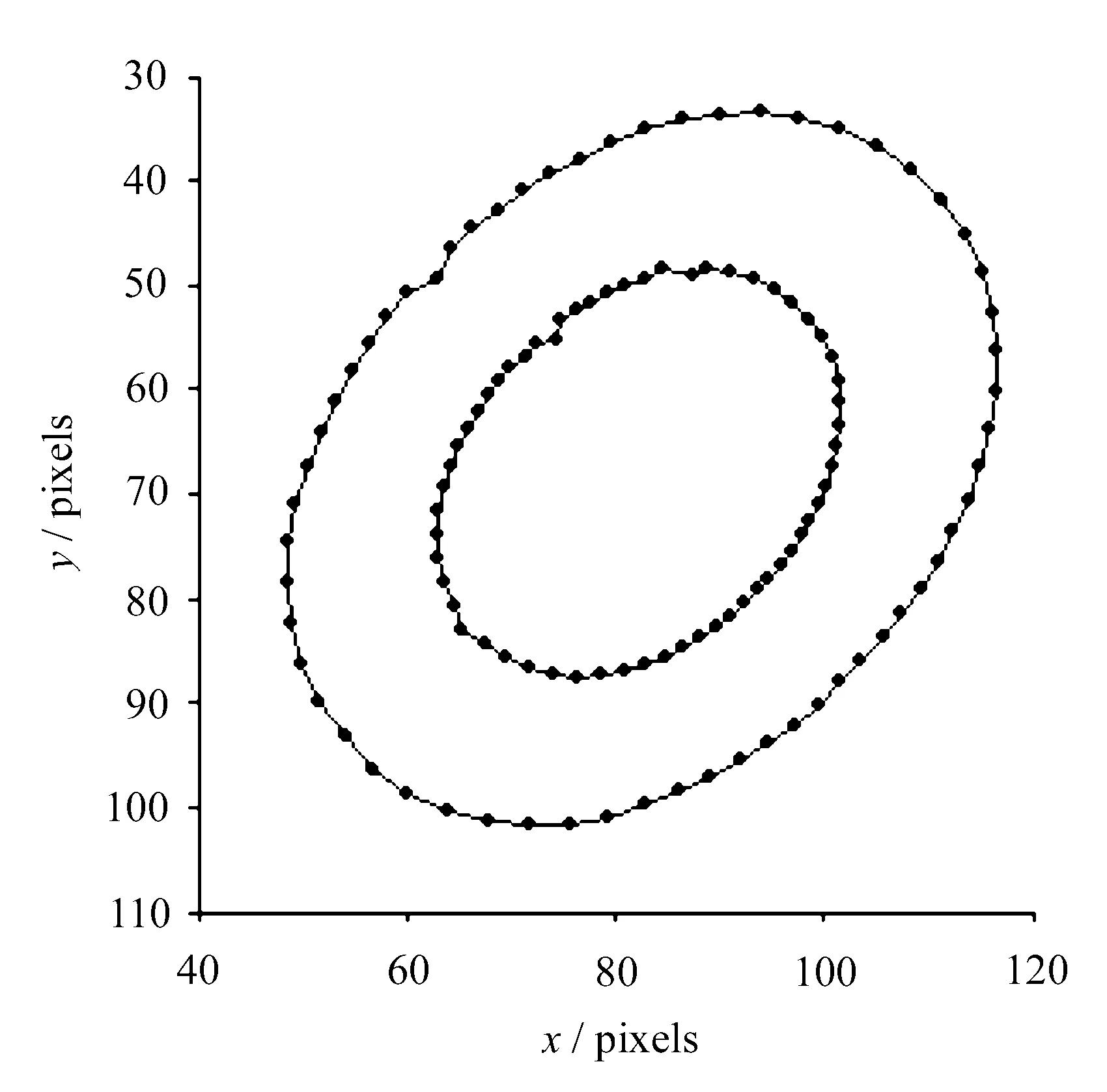
(a) 滤波前

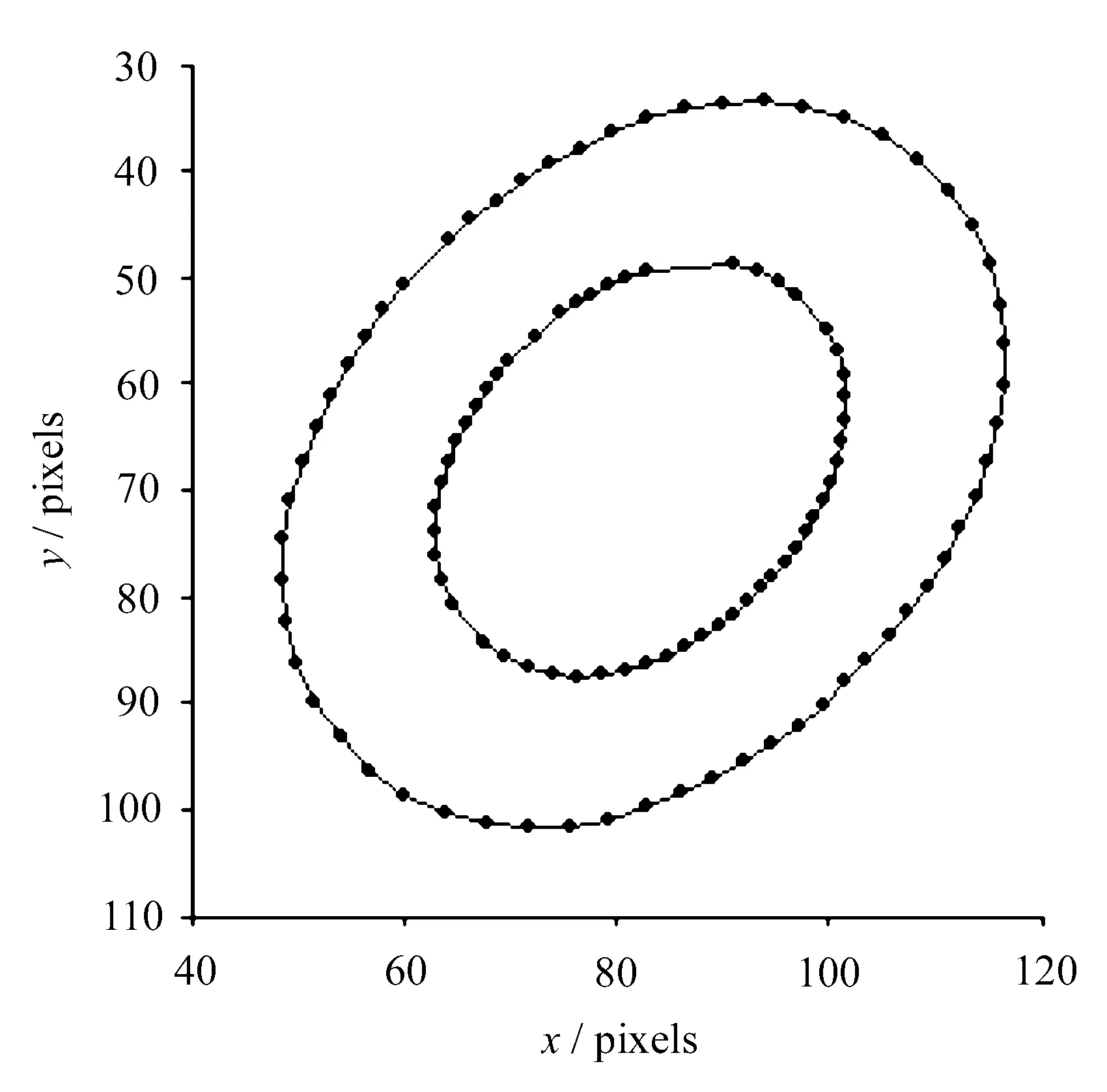
(b) 滤波后

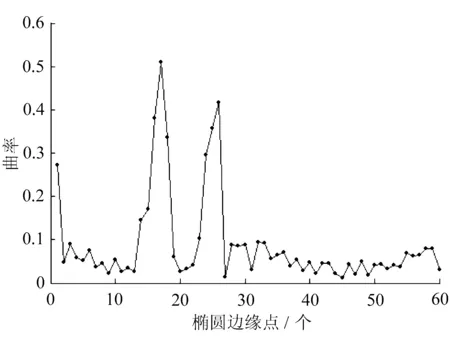
(a) 滤波前

(b) 滤波后

1.4椭圆边缘点的精确提取以及同心圆投影中心定位

在对椭圆边缘点进行滤波后，对椭圆进行最小二乘拟合，设获得椭圆的初始方程为:

(6)

根据椭圆方程可求得椭圆上任意点P(xp,yp)的梯度斜率kg为:

(7)

在上述的椭圆边缘检测中，没有严格在边缘点的梯度方向上对边缘点进行定位，所以将带来一定的边缘定位误差。为了获得更高精度的椭圆方程，需在椭圆边缘点附近邻域内沿着式(7)所确定的梯度方向对椭圆边缘点重新进行亚像素级边缘检测和曲率滤波，然后对两个椭圆的方程重新进行最小二乘曲线拟合。

设拟合后的两椭圆方程分别为F1(x,y)和F2(x,y)，两椭圆的几何中心为O1和O2。过两椭圆的几何中心O1和O2作一条直线L，该直线与两椭圆的交点分别为A1,A2,B2,B1，如图5所示。

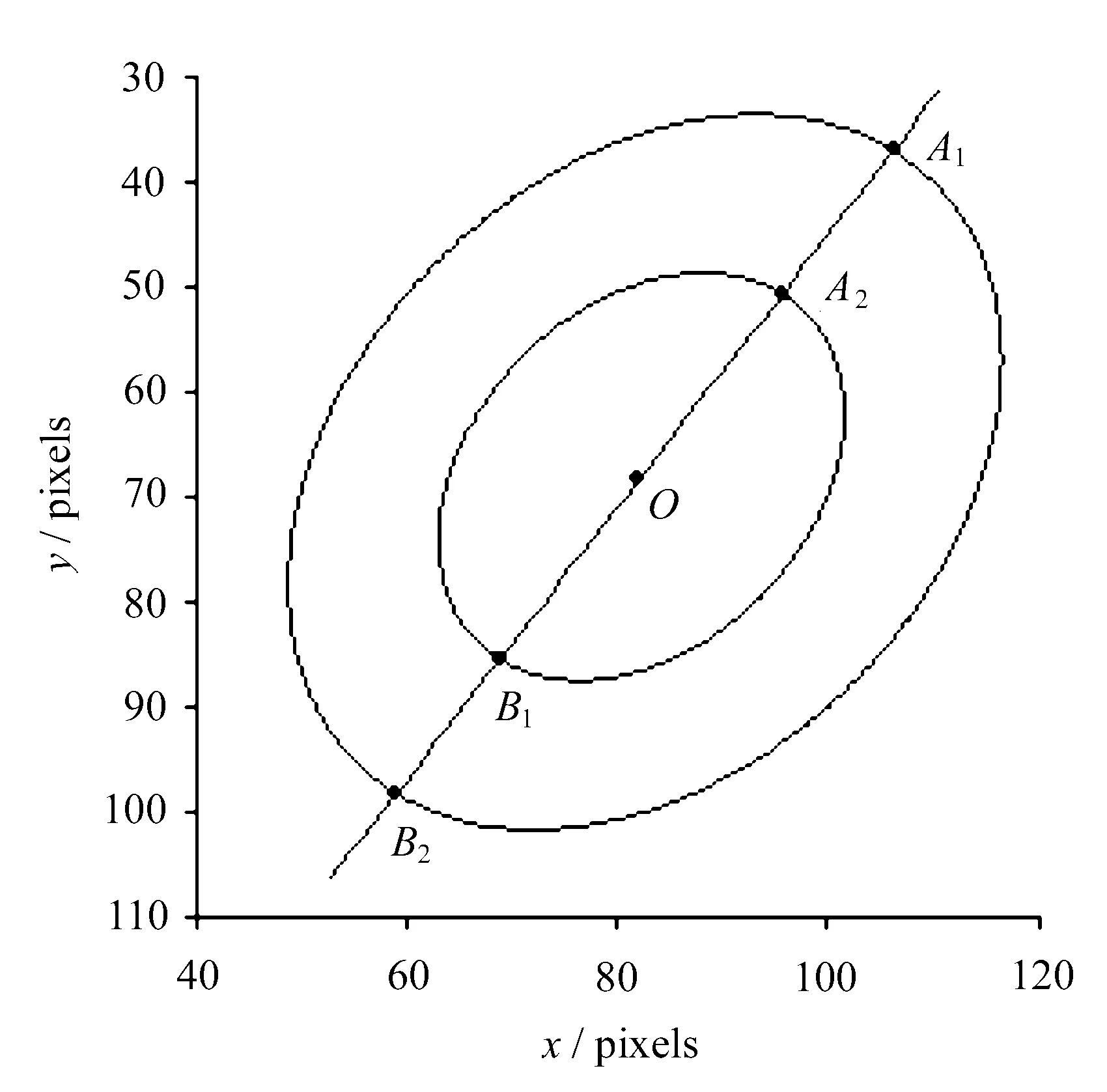
图5 同心圆投影中心定位原理图

则同心圆的投影中心O可由仿射变换交比不变原理求得:

(8)

2 同心圆投影中心定位实验

为了对文中算法的精度进行分析，生成了同心圆测试图像。

首先绘制带有同心圆环和角点模板，然后用3*3的滤波器对该图像进行平滑，用以模拟摄像机拍摄中所产生的渐变效应，从而生成标准测试图像，如图6所示。

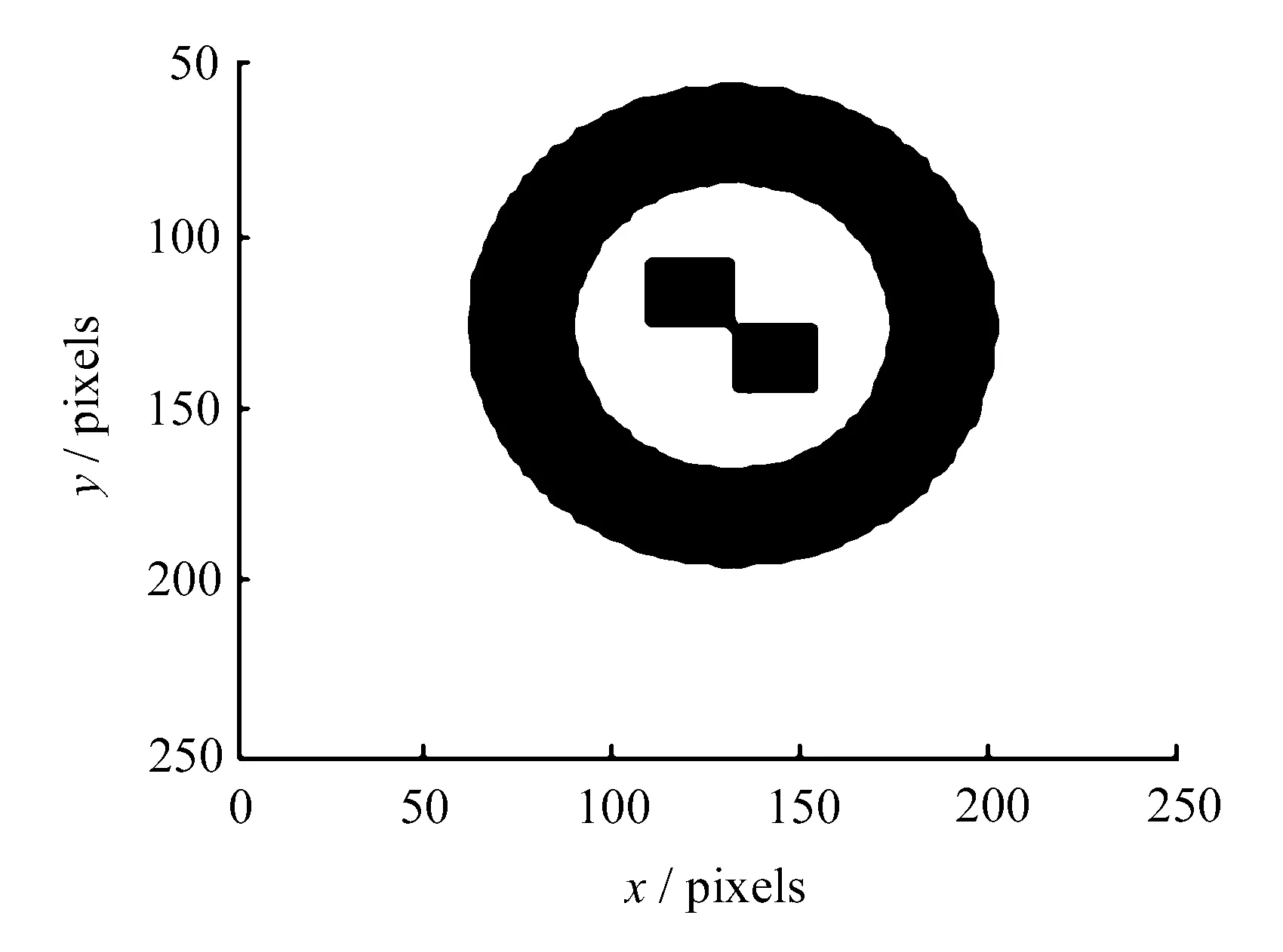
图6 同心圆环标准测试图像

然后对该图像进行不同的单应矩阵变换和坐标平移，用以模拟不同角度的摄像机拍摄图像，如图7所示。

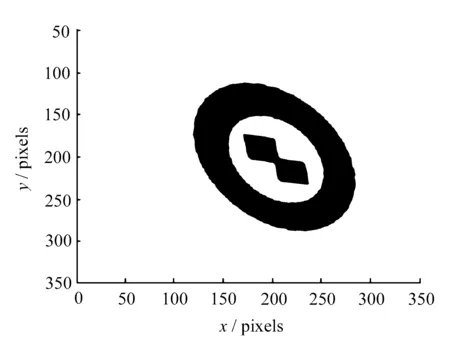
图7 经单应变换的同心圆环测试图像

图7图像的同心圆环投影中心实际值可由图6图像的圆环中心实际值经单应矩阵变换和坐标平移得到。

文中首先分析了高斯平滑滤波器、一阶高斯边缘检测算子对测量精度的影响，分别如图8～图10所示。

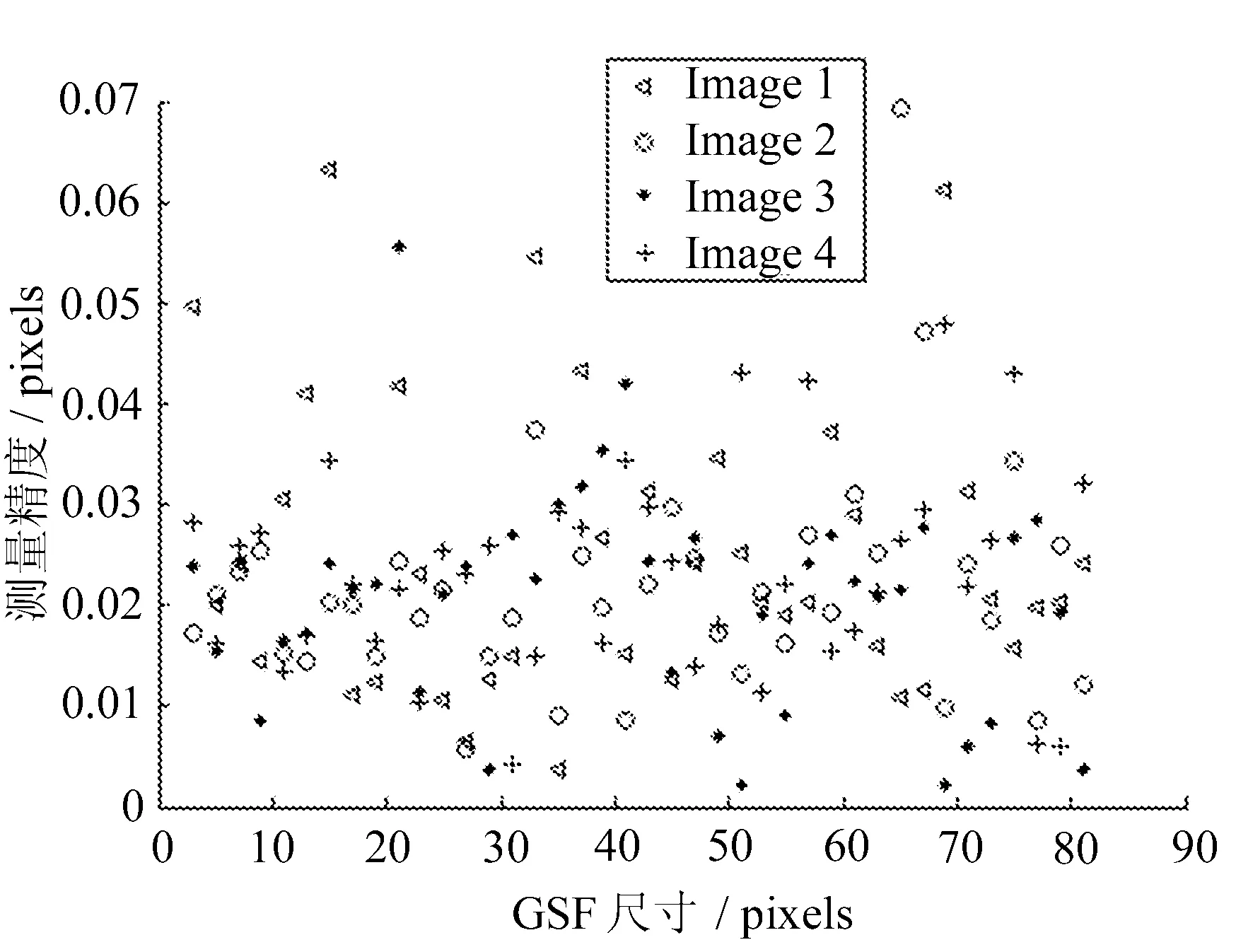
图8 不同GSF尺寸的误差分析 (SNR: 41 dB)

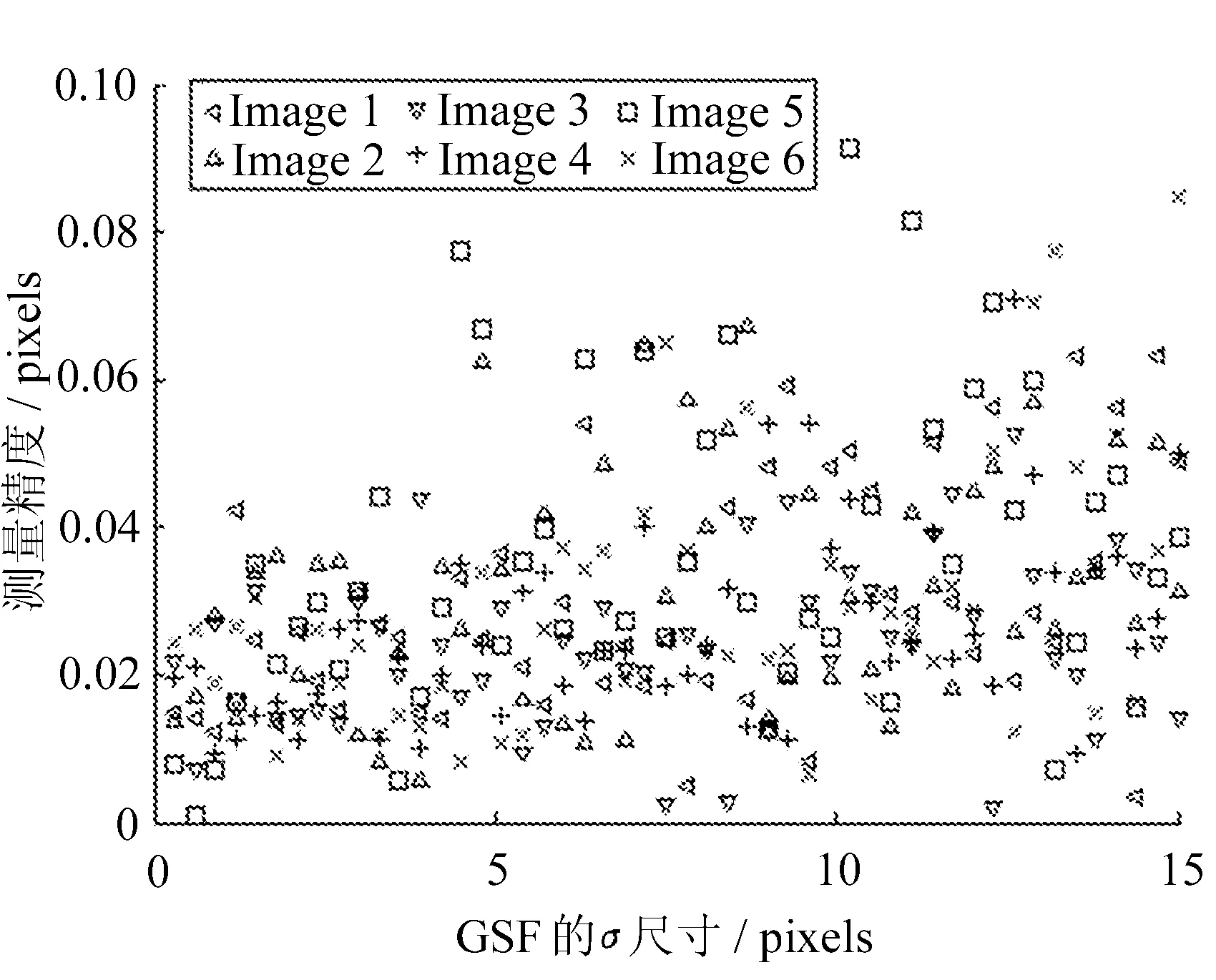
图9 GSF不同σ的误差分析 (SNR: 41 dB)

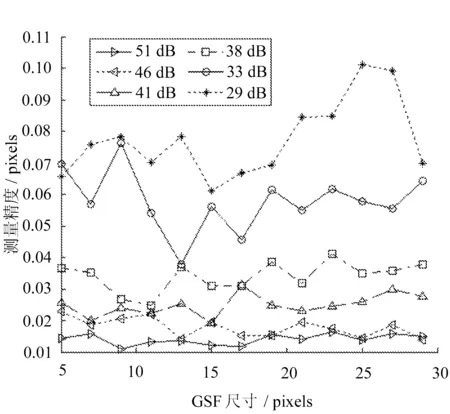
图10 不同GEF尺寸的误差分析

由图8可知，当高斯平滑滤波器的尺寸在4～10 pixels之间时，测量误差较小；由图9可知，当σ≤4.2时，测量误差较小；由图10可知，边缘检测算子尺寸在11～13 pixels之间时，测量误差较小，而且随着噪声的增加，测量误差有明显的上升趋势。

最后，分别用文中的同心圆法、角点定位法对测试图像进行了定位误差分析，如图11所示。

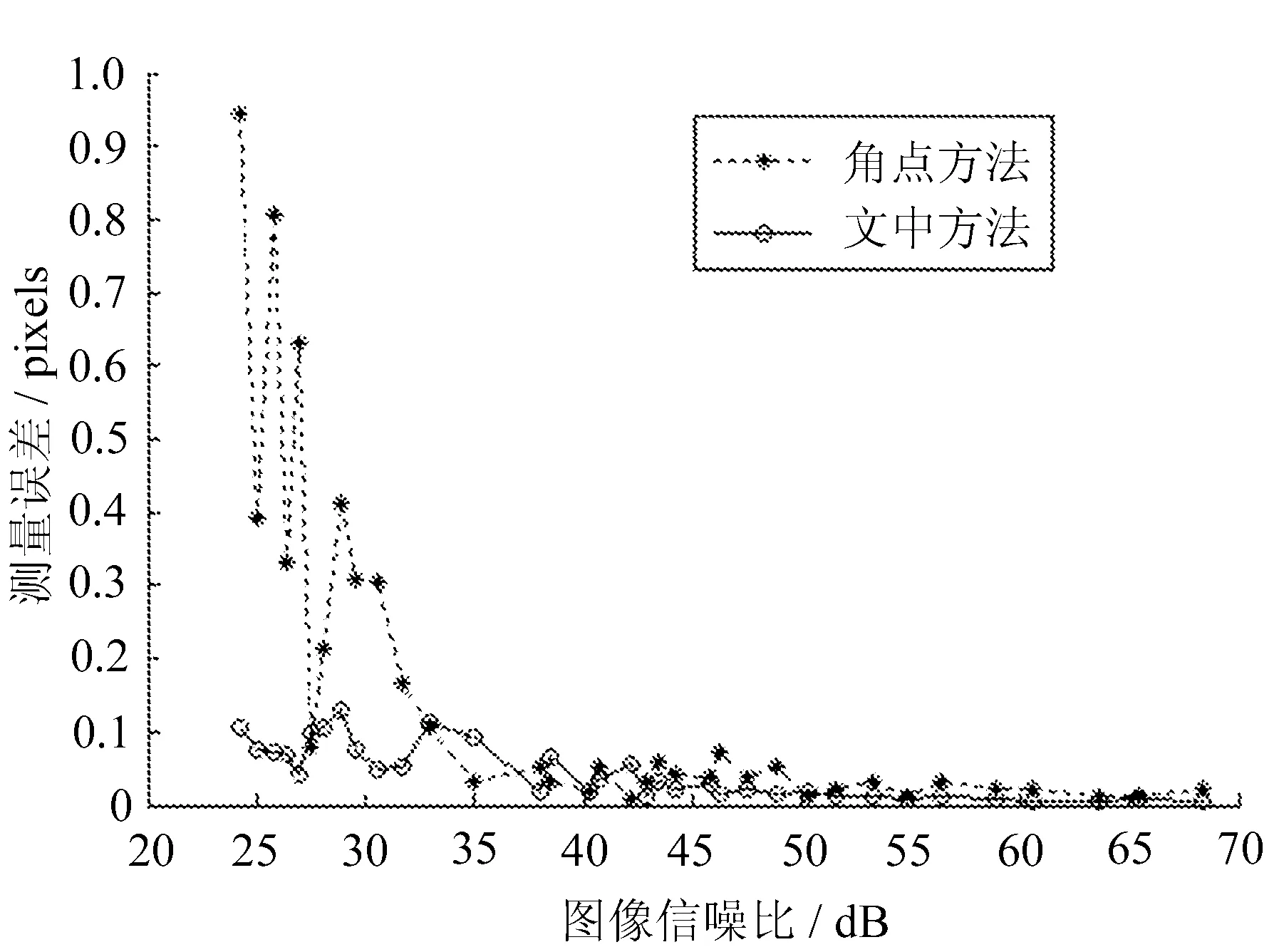
图11 文中方法与角点检测法的像素误差对比

由图11可知，当图像中存在噪声时，在信噪比大于35 dB时，文中方法与角点法的测量误差均小于0.1 pixel;当信噪比介于35 dB和25 dB之间时，角点检测法的测量误差突然急剧增大，而文中方法的测量误差变化仍比较平缓，测量误差小于0.15 pixel。

3 结 语

提出了采用经过曲率滤波的椭圆曲线拟合法与射影交比不变法相结合来实现对同心圆的投影中心进行的亚像素定位。并采用单应矩阵变换和坐标平移法生成了大量的理想测试图像，将文中方法与角点检测法的测量精度进行了比较分析，结果表明，文中方法的测量精度在有无噪声情况下均高于角点检测方法。

[1] Jun-Sik Kim, In-So Kweon. A New Camera Calibration Method for Robotic Applications[C]// International Conference on Intelligent Robots and Systems.2001:778-783.

[2] Ashutosh Morde, Mourad Bouzit. Lawrence Rabiner[C]//A Novel Approach to planar camera calibration, " International Conference on Computer Vision Theory and Applications.2006:87-92.

[3] X H Ying, H B Zha. Efficient detection of projected concentric circles using four intersection points on a secant Line[C]//International Conference on Pattern Recognition.2008：1-4.

[4] Junpeng Xue, Xianyu Su, Liqun Xiang, et al. Using concentric circles and wedge grating for camera calibration[J]. Applied Optics,2012,51(17):3811-3816.

[5] Chris Harris, Mike Stephens. A combined corner and edge detector[C]//Proceeding of the 4th Alvey Vision Conference.1988:147-151.

[6] Li L F, Feng Z R, He K L. A randomized algorithm for detecting multiple ellipses based on least square approach [J]. Opto-electronics Review,2005,13(1):61-67.

[7] Halir R, Flusser J. Numerically stable direct least squares fitting of ellipses[C]// International Conference in Central Europe on Computer Graphics and Visualization.1998:125-132.

[8] 王毅，徐成杰.基于多目标规划的飞机使用计划模型研究[J].长春工业大学学报：自然科学版，2009,30(1):73-77.

Concentric circle sub-pixel center positioning method

ZHANG Fang-cheng, LI Xiao-tian

(Changchun Institute of Optics and Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033， China)

A location method for concentric circles' projection center based on ellipses’curve fitting and curvature filter is put forward. The test images are generated with homography transform and coordinate shift, and the method is compared with the corner detection. The results show that the accuracy of the method is better than that of corner detection no matter how the images have noise or not. When images’ S/N ratio is between 25～35 dB, the error of the corner detection increases sharply while that of concentric circle method is only up to 0.15 pixel.

machine vision; image processings; concentric circle calibration; ellipse fitness.

2014-08-22

国家重大科研装备研制基金资助项目(ZBYZ2008-1)

张方程(1958-)，男，汉族，河北宁津人，中国科学院长春光学精密机械与物理研究所工程师，主要从事衍射光栅镀膜工艺及检测技术方向研究,E-mail:zhangfc_ciomp@163.com.

TP 311.5

A

1674-1374(2014)05-0500-06