数值级数法求解一类时滞微分方程

邱 宁

(青岛理工大学琴岛学院， 山东 青岛 266106)

数值级数法求解一类时滞微分方程

邱 宁

(青岛理工大学琴岛学院， 山东 青岛 266106)

采用级数形式给出半离散差分格式在网格节点处的数值解以及计算级数中的每一项递推公式。离散后差分格式收敛性、稳定性分析表明该格式收敛且稳定，数值算例验证该方法有效。

时滞微分方程; 数值级数法; 收敛性; 稳定性

0 引 言

延迟微分方程是描述众多物理现象的一类方程之一，目前对延迟微分方程解析解的性质研究的文献较多[1-8]，而对数值解的研究较少。文中利用数值级数法求解一类初边值时滞微分方程。

(1)

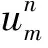
(2)

对vk(xm,tn)给出递推公式进行精确计算，在数值算例中只需取级数前8项就可以达到很高的精度。

1 数值级数法格式的构造

xm=mh

tn=nΔt

将式(1)在点(xm,t)处半离散得到

(3)

在区间[tn,t],t∈(tn,tn+1]上对式(3)积分得到

(4)

(5)

由式(5)给出递推公式:

(6)

当m=0时，

(7)

当m=M时，

(8)

当m=1,2,…,M-1时，将t=tn,t=tn+1分别代入式(6)，利用梯形积分公式得

(9)

和

(10)

则可以得到

(11)

2 收敛性证明

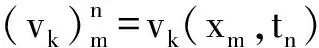
(12)

写成矩阵方程的形式为：

(13)

其中

由文献[4]知式(11)收敛。

3 稳定性证明

定理2 数值级数格式(10)无条件收敛。

证明 在等式

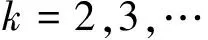
(14)

(15)

根据式(11)进一步整理得

(16)

相应得出误差关系式：

(17)

写成矩阵方程：

(18)

进一步写成

(19)

其中C=tridiag(r,-r)。

由文献[4]知成立误差估计

(20)

其中,ε0=(1+2k1τ)‖E0‖2,稳定性证毕。

4 数值算例

精确解为:

u(x,t)=x2+t2

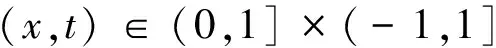
在数值计算时取Δt=0.005,取级数前8项，计算结果见表1。

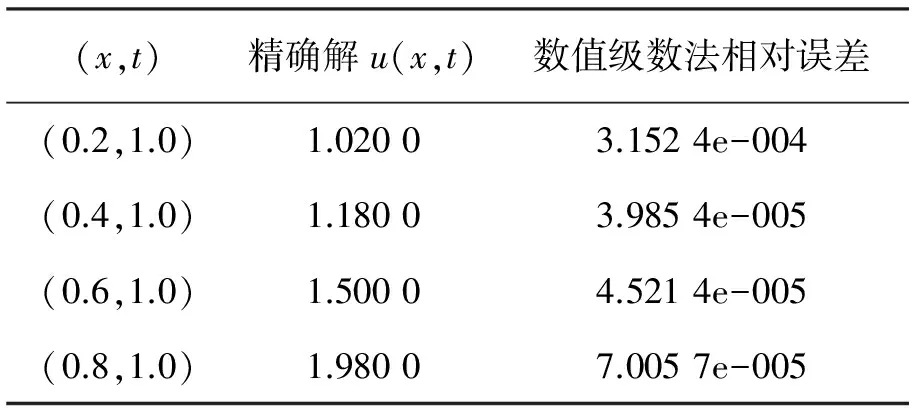
表1 数值解的相对误差

从表1可以看出，数值级数法解决此类问题是一个有效的方法。

[1] 刘安平,肖莉,刘婷,等.抛物型时滞偏微分方程解振动的充要条件[J].纯粹数学与应用数学,2003,19(3):231-233.

[2] Jin Cheng Ri, Liu Ming Zhu. A new modification of adomian decomposition meehod for solving a kind of evolution equation [J]. Appl.Math.Comput,2005,169(2):953-962.

[3] 刘安平.非线性中立双曲型偏微分方程解的振动性质[J].应用数学与力学,2002,23(6):604-610.

[4] 刘明鼎.数值级数法求解时滞抛物型方程[J].曲阜师范大学学报：自然科学版,2014,40(1):38-41.

[5] 郭长勇,赵景军,刘明珠.二阶延迟微分方程解析解的渐近稳定性[J].黑龙江大学学报：自然科学版,2002(3):5-7.

[6] 刘丽环,常晶,高艳超.二阶常微分方程边值问题的格林函数求法[J].长春工业大学学报：自然科学版,2011，32(1):102-104.

[7] 杜颖,梅长林.一类具有分布式记忆的带跳随机延迟微分方程半隐式欧拉数值解的收敛性[J].工程数学学报,2014(2):215-228.

[8] 谭英贤,甘四清,王小捷.随机延迟微分方程平衡方法的均方收敛性与稳定性[J].计算数学,2011(1):25-36.

Numerical series method for delay differential equation

QIU Ning

(Qingdao Technological University Qindao College, Qingdao 266106， China)

Numerical series is used to express the numerical solution of half-discrete differential equation and every recursion formula. Both the example and the analysis of the convergence and stability for the differential equation show that the numerical series method is feasible.

delay differential equation; numerical series method; convergence; stability.

2014-05-08

邱 宁(1980-)，女，汉族，山东烟台人，青岛理工大学琴岛学院讲师,硕士，主要从事非线性振动控制和稳定性分析方向研究,E-mail:524916281@qq.com.

O 175.26

A

1674-1374(2014)05-0589-04