生产函数规模报酬与结构性变点估计

张海燕, 张海波

(1.长春工业大学 基础科学学院， 吉林 长春 130012;2.福建宁德核电有限公司 工程管理部, 福建 宁德 355209)

生产函数规模报酬与结构性变点估计

张海燕1, 张海波2

(1.长春工业大学 基础科学学院， 吉林 长春 130012;2.福建宁德核电有限公司 工程管理部, 福建 宁德 355209)

基于C-D生产函数模型，采用改进最小二乘法检验规模报酬和结构性变点。首先，在最小二乘估计程序中加入规模报酬不变的约束，然后通过Wald统计量检验约束和无约束模型的差异性，以确定规模报酬情况。进行样本区间划分，在全样本区间和分段样本区间参数估计之后，通过Chow统计量检验参数的差异性，以确定结构性变点。以我国1980-2007年的数据为例，规模报酬是变化的，1986年和1994年均为结构性变点。

C-D生产函数； 规模报酬； Wald统计量； 结构性变点； Chow统计量

0 引 言

生产函数表示在一定时期内，在技术水平不变的情况下，生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系，反映了在既定的生产技术条件下投入和产出之间的数量关系[1]。这种数量关系的数学表达有多种形式，一般分为短期生产函数和长期生产函数[2]。其中C-D生产函数[3]以其易于线性化和参数具有经济意义而受到研究人员的广泛关注。文中将利用C-D生产函数，通过改进最小二乘法、Wald统计量和Chow统计量检验我国生产函数中的规模报酬和结构性变点问题。

1 生产函数规模报酬的确定

首先根据C-D生产函数特征给出规模报酬的不同类型，然后运用我国1980-2007年GDP、固定资产投资和劳动的数据确定规模报酬的具体类型。

1.1生产函数规模报酬的确定

C-D生产函数的形式为

式中:Y----国内生产总值；

A(t)----综合技术水平；

L----投入的劳动力人数，万人；

K----投入的资本，使用固定资产投资，亿元；

α----劳动力产出的弹性系数；

β----资本产出的弹性系数；

μ----随机项。

其线性化形式为

(1)

规模报酬[4](Returns to Scale)属于长期生产理论问题，是指在其它条件不变的情况下，各种生产要素按相同比例变化时所带来的产量变化，对于C-D生产函数来说，根据α和β的取值情况分为3类。当α+β>1时，称为递增报酬型，表示按现有技术用扩大生产规模来增加产出是有利的；当α+β<1时，称为递减报酬型，表示按现有技术用扩大生产规模来增加产出是得不偿失的；当α+β=1时，称为不变报酬型，表示生产效率并不会随着生产规模的扩大而提高，只有提高技术水平，才会提高经济效益。

1.2规模报酬类型的确定

首先，在没有任何限制的条件下，对模型(1)参数进行最小二乘估计。然后，将规模报酬不变的经济理论公式化，即以约束条件β1+β2=1的形式加入最小二乘程序来估计参数[5]。最后，对无约束条件下的回归残差和有约束条件下的回归残差进行比较,以确定规模报酬类型。

无约束条件下回归结果为:

ln(Y)=-4.82+0.76ln(L)+0.74ln(K)

(2)

调整R2为0.996，说明回归模型的拟合优度较好。弹性系数参数估计的P值均小于0.05，说明劳动和资本的参数均显著。

现在考虑规模报酬不变理论，将约束条件β1+β2=1加入最小二乘估计附有线性约束条件的模型。规模报酬不变约束下最小二乘估计结果见表1。

由于强行加入的约束条件，以残差为基础的标准统计量只有在约束条件正确时才可靠。Wald检验统计量[5]是采用限制模型和非限制模型的残差平方和(RSS)来检验采用约束条件的模型是否与没有约束条件的模型具有统计意义上的不同。

(3)

式中:RSS*----在约束条件β1+β2=1下的残差平方和；

RSS----没有限制条件的残差平方和；

J----限制条件个数；

K----变量的个数，包括常数项；

N----观测个数。

计算结果为:

F(1，25)分布的0.05临界值为4.20，计算的Wald检验统计量数值5.001 4位于F分布的右尾拒绝区域内，相应的P值为0.034 5,小于0.05。因此，拒绝线性约束条件假设β1+β2=1，即规模报酬是变化的。

2 生产函数结构性变点的确定

生产函数的结构性变点是指在某一年由于发生了一些重大事件或国家出台了重要的政策，从而对经济发展产生了较大的影响，但不一定是当年显现，也可能是在之后几年才显示出对经济发展的影响。由于受到这个影响，产出的数值可能突然会发生较大的变化，那么发生变化的这个时间点就是结构性变点。

采用下式表示的Chow统计量[6]，检验1980-2007年间的实际产出是否在某一年发生了结构性变化，即涵盖所有期间的回归系数与两个划分的时间期间回归系数之间进行比较，如果发现它们在统计意义上具有显著的差异，就可以确定在这一年之后生产力出现了结构性的变化。

(4)

式中:RSS*----受到约束的整个样本的残差平方和；

RSS1----第一个子样本的残差平方和；

RSS2----第二个子样本的残差平方和；

K----每个回归总的变量个数，包括常数项；

N----整个样本观测期；

J----约束条件的个数。

这里原假设为，检验的这一年不存在结构性变点[7]。首先，通过F分布的分布表查出5%显著水平下F分布的临界值[8]，将之与由公式计算出的统计量值比较确定结构性变点是否存在。

首先检验1986年是否为结构性变点。参数估计过程将3次调用最小二乘估计的程序，第1次估计整个样本，第2次估计1980-1986年样本期间的参数，第3次估计1987-2007年样本期间的参数。

1986年作为结构性变点3次最小二乘估计结果见表2。

表1 规模报酬不变约束下最小二乘估计结果

表2 1986年作为结构性变点三次最小二乘估计结果

由表2可见，整个样本参数估计的残差平方和RSS*=0.150 6，第1个子样本期间参数估计的残差平方和RSS1=0.003 595 4，第2个子样本残差平方和RSS2=0.086 825，限制条件的个数J=3，样本总量N=28，包括常数项的变量个数K=3，则可以计算Chow统计量为:

查表可得5%显著性水平下，F(3,22)的临界值为3.05，小于Chow检验统计量4.88，因此拒绝原假设，即1986年为结构性变点。同样的方法检验1990,1991,1992,1994,1995，1996年是否为结构性变点，结果发现,1992,1994,1995年均可视为结构性变点。为了进一步确定1994年前后的转折点，将样本期间划分为3个部分，同时分析两个结构性变点是否显著。参数估计过程中将4次调用最小二乘估计程序，第1次估计整个样本期间的参数，第2次估计1980-1986年间的参数，再将1987-2007年数据分别以1992,1994,1995年加以划分，进行第3次和第4次参数估计。结果发现1986年和1994年作为结构性变点是显著的，估计结果见表3。

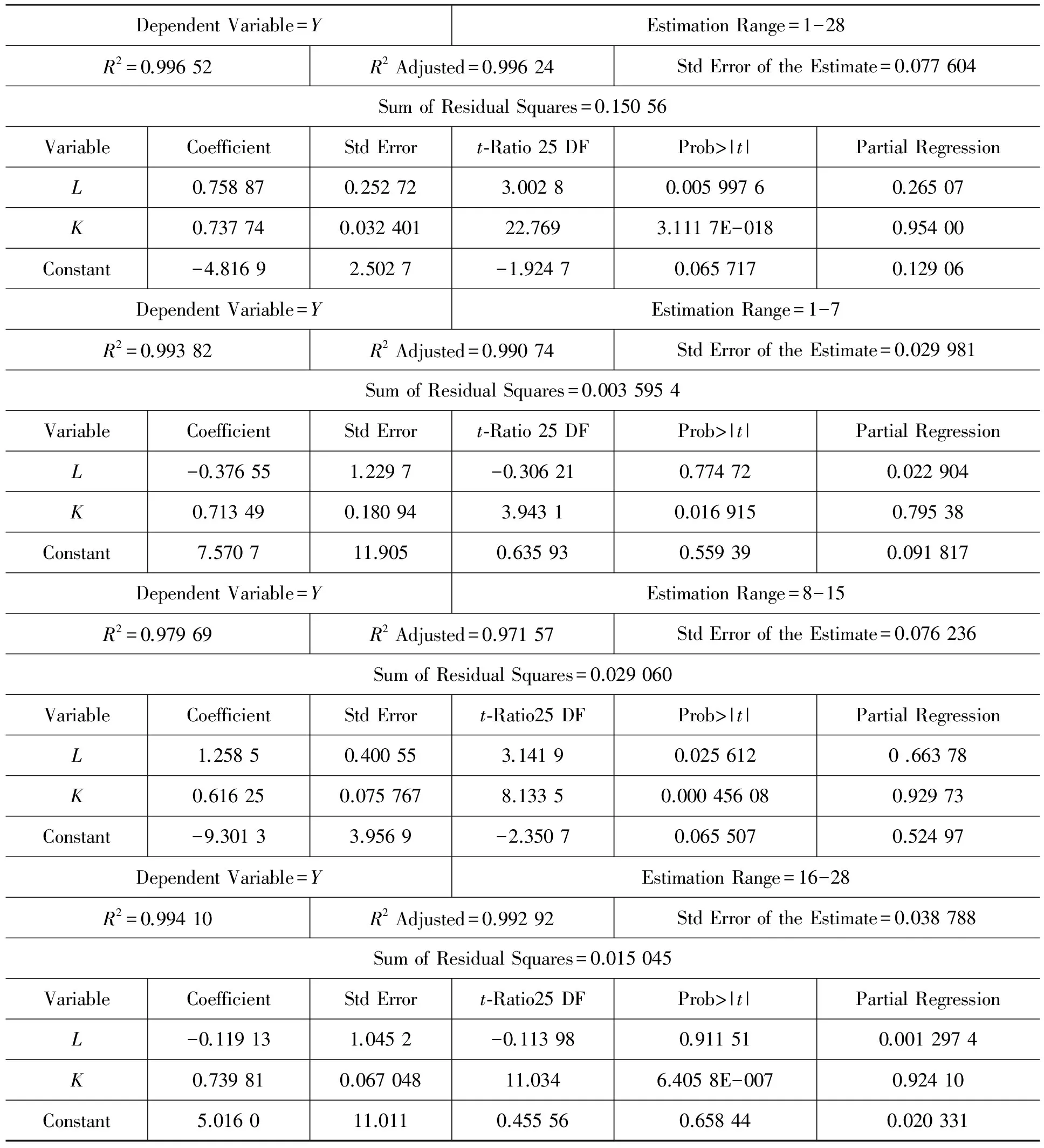
表3 1986年和1994年作为结构性变点4次最小二乘估计结果

在表3的估计过程中增加了限制条件，因此Chow检验统计量的形式改变为:

(5)

由表3整个样本期间参数估计的残差平方和RSS*=0.150 6，第1个子样本残差平方和RSS1=003 595 4，第2个子样本的残差平方和RSS2=0.029 060，第3个子样本的残差平方和RSS3=0.015 045，限制条件的个数J=4，样本总量N=28，包括常数项的变量个数K=3。则Chow统计量计算结果为:

查表可得5%的显著性水平下F(4, 19)分布的临界值为2.90,小于Chow统计量10.245，因此拒绝原假设，可以认为1986年和1994年均显著为结构性变点。

3 结 语

使用C-D生产函数模型，通过约束最小二乘法运用Wald统计量检验了我国1980-2007年生产函数的规模报酬情况，发现规模报酬在该样本期间是变化的。对于C-D生产函数进一步通过多次调用最小二乘法，运用Chow统计量检验我国生产函数的结构性变点，确定了1986年和1994年为转折点。1978年的十一届三中全会后，我国实行了改革开放政策，把工作重心转移到了经济建设上，出台了一系列有利于经济发展的政策，促使经济开始快速发展，可以认为，1978-1986年劳动和资本的产出弹性保持不变。1987年我党提出了“一个中心，两个基本点”的政策，1988年邓小平同志提出了“科学技术是第一生产力”的口号，通过进一步的改革措施，经济增长形式发生转变直至1993年。1994年国务院作出《关于深化城镇住房制度改革的决定》，明确城镇住房制度改革的基本内容，其中包括把住房实物福利分配的方式改变为以按劳分配为主的货币工资分配方式、建立住房公积金制度等。这一政策奠定了国内住房商品化的基础，形成经济的新增长点，人民生活水平显著提高[9]。根据上述分析发现，在经济增长转折点前后都有影响经济发展的较重要的政策出台或者重大事件发生，从而影响到经济的增长。因此，文中数据分析结果是合理的。

[1] 高鸿业.西方经济学[M].2版.北京：中国人民大学出版社，2001.

[2] 许纯祯，吴宇晖，张东辉.西方经济学[M].北京：高等教育出版社，2005.

[3] Mankiw N G. Principles of economics [M].3rd Edition.[S.l.]: South-Western College Pub,2003.

[4] 曼昆.经济学原理[M].梁小民,译.2版.北京：机械工业出版社，2003.

[5] 林广平.计算计量经济学[M].北京：清华大学出版社，2003.

[6] 李子奈.高等计量经济学[M].北京：清华大学出版社，2001.

[7] 李子奈.计量经济学[M].北京：高等教育出版社，2001.

[8] 何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2001.

[9] 何大强，张海燕.吉林省农村居民消费水平分析[J].长春工业大学学报：自然科学版，2013，34(4)：452-456.

Estimation of structural change-point and production function

ZHANG Hai-yan1, ZHANG Hai-bo2

(1.School of Basic Science, Changchun University of Technology, Changchun 130012， China;2.Project Management Department, Fujian Ningde Nuclear Power Co., Ltd., Ningde 355209， China)

Based on C-D production function model, the restricted Least Square (LS) method is applied to test Returns-to-scale and structural change-point. First, a constant restraint of Returns-to-scale is added to LS program, and then the difference between the model with and without restraint is identified with Wald-statistics to determine the Returns-to-scale. Parameter differences are tested in both the whole sampling period and the divided sampling section with Chow-statistics to determine the structural change-point. With the data in China from 1980 to 2007, Returns-to-scale is changed, while the of 1986 and 1994 are structural change-points respectively.

C-D production function; returns-to-scale; wald-statistics; structural change-point; Chow-statistics.

2014-05-20

国家自然科学基金资助项目(11071026)； 教育部人文社会科学研究基金资助项目(12YJA790187)； 吉林省教育厅“十二五”社会科学研究项目(吉教科文合字[2014]第57号)； 吉林省科技发展计划项目(20140418053FG)

张海燕(1970-)，女，汉族，吉林长春人，长春工业大学教授，博士，主要从事经济增长和经济波动方向研究,E-mail:zhanghaiyan@mail.ccut.edu.cn.

F 037.1

A

1674-1374(2014)05-0481-06