无线传感器网络FM模型实时性分析
曹英武, 罗新宇, 张冰川
(长春理工大学 电子信息工程学院, 吉林 长春 130022)
无线传感器网络FM模型实时性分析
曹英武, 罗新宇, 张冰川
(长春理工大学 电子信息工程学院, 吉林 长春 130022)
为确保Wireless Sensor Network(WSN)传感器节点对已获取信息实时计算与零延时传输,构建了栅格WSN的三维Fornasini-Marchesini(FM)模型,提出了两种解决方案。重点讨论了系统传递函数矩阵满足的约束条件。
无线传感器网络; FM模型; 传递函数矩阵; 栅格
0 引 言
无线传感器网络正在逐渐改变着人们的生活方式,它通过分布在空间上的大量传感器节点间的相互协同作用对信息进行收集,并发送给观察者,为其提供一些必要的信息[1]。由于其自身具有低功耗、低成本和快速组网等特点,ZigBee无线传感器网络被广泛应用在医疗领域[2]。根据传感器节点空间部署方式,传感器网络按节点部署可分为三大类:随机部署、规则部署、特定应用部署。鉴于随机部署的传感器网络需要克服传感器节点随机放置的不确定性产生的冗余,从而导致系统成本昂贵;而特定应用部署的传感器网络应用场合又十分有限。考虑以上两点,规则部署传感器网络逐步引起人们的关注。规则部署传感器网络模式如图1所示。
规则部署传感器网络是由三角晶格、正方形、正六边形通过空间二维镶嵌而成。由传感器节点部署在矩形网格顶点上形成的规则部署传感器网络被称为栅格型无线传感器网络。
对于多维系统理论在传感器网络中的研究,文献[3]提出将二维系统中研究的相关理论直接推广到三维系统中;文献[4]提出将三维系统中的问题规约到二维系统中研究。然而有些问题并不是可以通过上述两种方法就可以解决的。无线传感器网络的实时性问题并不是通过推广或是规约就能解决。
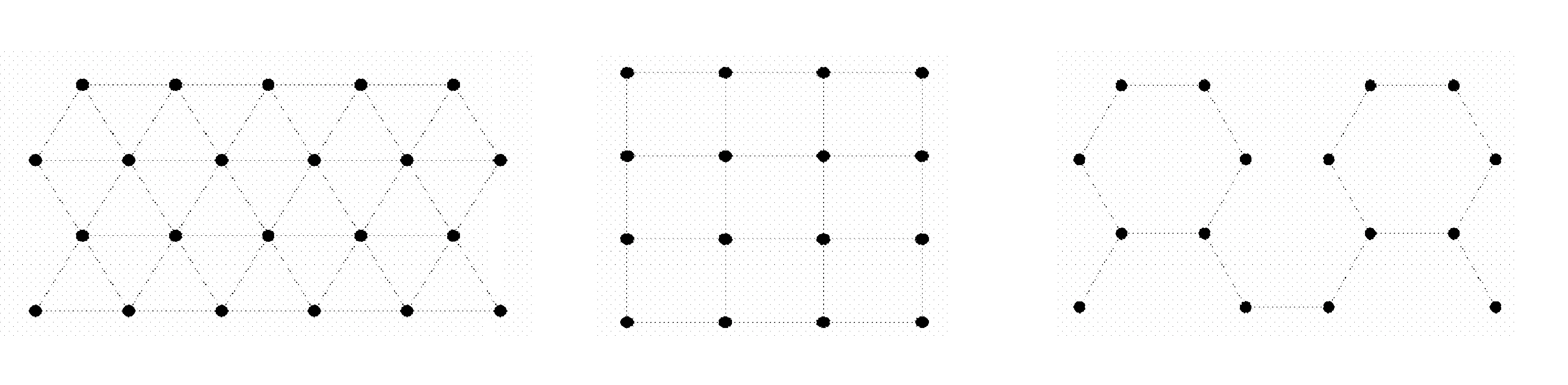
(a) 三角晶格 (b) 正方形 (c) 正六边形
1 栅格传感器网络FM模型实现
针对三维FM[5]模型的构建,文献[6-7]提出基于FM下栅格型传感器网络的分布式信息处理理论。由于二维栅格传感器网络中多个传感器节点在多个采样时段内完成的运算可构成一个三维线性系统,所以该理论可以直接应用于线性栅格传感器网络系统。
三维系统FM模型如下:
(1)
这里x∈Rn的状态向量,n1,n2,t分别表示三维空间中水平方向、垂直方向、时间方向上的节点坐标。n1∈Z,n2∈Z,且t∈Z。设输入状态向量u∈Rp,输出状态向量y∈Rq。At,Av,Ah,Bt,Bv,Bh分别表示系统状态方程中时间方向、垂直方向、水平方向上的状态矩阵和输入矩阵。At∈Rn×n,Av∈Rn×n,Ah∈Rn×n,Bt∈Rn×p,Bv∈Rn×p,且Bh∈Rn×p。C,D分别表示系统输出方程中状态矩阵和输入矩阵。C∈Rq×n,D∈Rq×p。
设传感器网络的尺寸大小为N1×N2。N1,N2分别表示水平和垂直方向上节点个数。模型(1)中,空间变量n1和n2分别表示传感器节点的水平和垂直坐标。因此0≤n1≤N1-1,且0≤n2≤N2-1。向量x(n1,n2,t),y(n1,n2,t)和u(n1,n2,t)分别表示节点(n1,n2)在时间间隙t上的状态向量、输出向量、输入向量。相邻节点状态向量的通信和运算如图2所示。
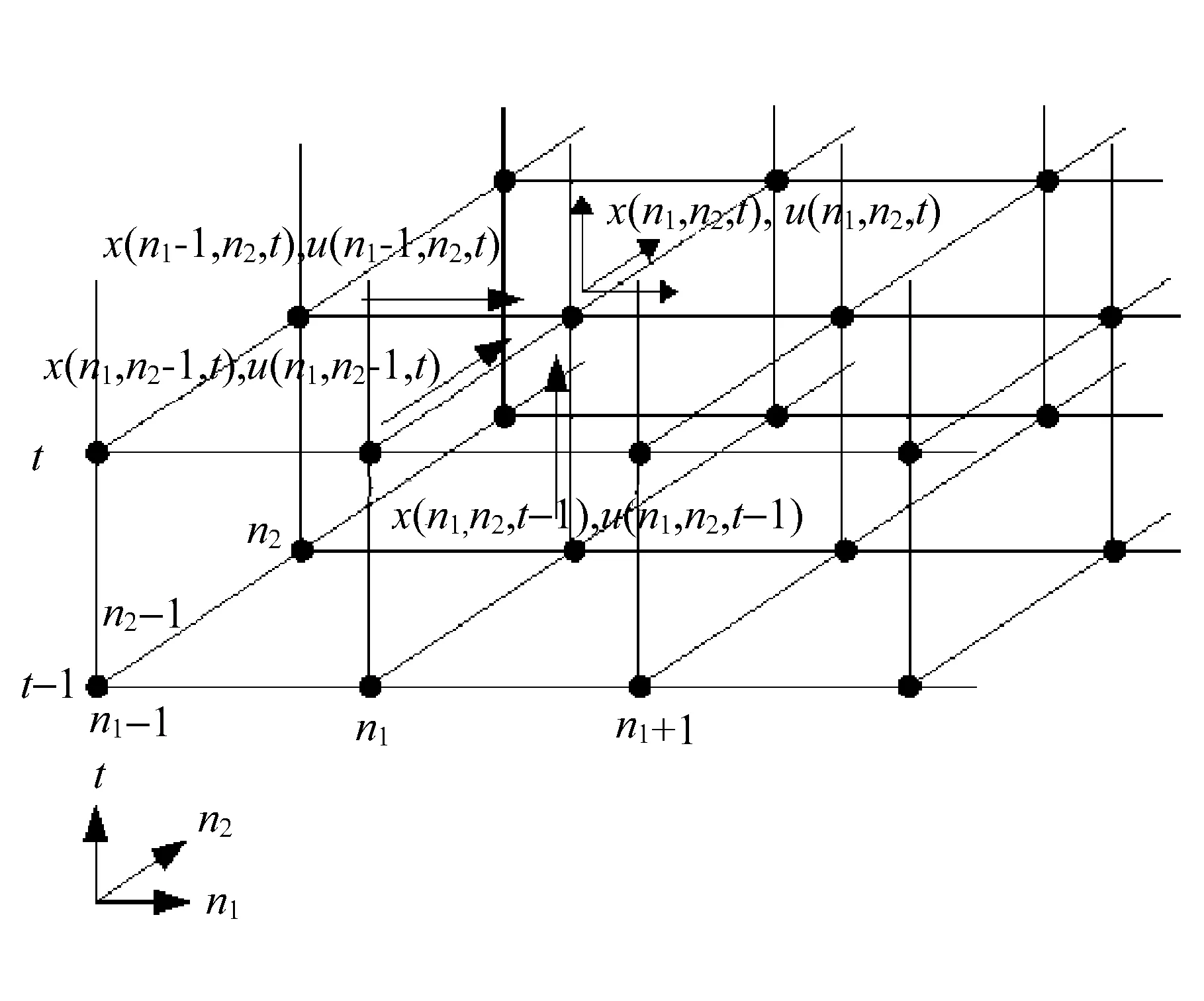
图2 相邻节点状态向量的通信和运算
由模型(1)知节点(n1,n2)在时间间隙t的运算过程如下:
1)状态向量x(n1,n2,t)接收状态向量为x(n1-1,n2,t)和x(n1,n2-1,t),输入向量u(n1-1,n2,t)和u(n1,n2-1,t)。
2)由模型(1)计算状态向量x(n1,n2,t)。
3)传递节点(n1,n2)的状态向量x(n1,n2,t)和输入向量u(n1,n2,t)给节点(n1+1,n2)和(n1,n2+1)。
4)由模型(1)计算输出状态向量y(n1,n2,t)。
2 实时实现问题
状态向量x(n1,n2,t)为节点(n1,n2)在时间间隙t的采样值。一个实时实现系统需要节点(n1,n2)在时间间隙t内完成计算的同时,节点(n1+1,n2)和(n1,n2+1)也完成计算。因此要实现数据零延时传送是难以实现的。有两种可供选择方案,用以解决此问题。
1)延迟响应实现:相邻节点间允许响应时间,这意味着系统并非实时的[7]。
2)实时实现:修改FM模型系统矩阵,使得仅有零延时数据以便于计算。
由于文献[8]针对GR模型实现对延迟响应进行了讨论且该结论可以直接推广到FM模型,所以文中对延迟响应实现在此将不做介绍。下面将针对实时实现展开论述。由模型(1)知:
(2)
同理得:
(3)
将式(2)代入式(3)得:
以此类推可知,实现水平、垂直方向零延时模型(1)应满足如下假设条件:

(4)
(5)
Atx(n1,n2,t-1)+Btu(n1,n2,t-1)可代替节点(n1,n2)状态向量x(n1,n2,t)在时间间隙t不能计算的信息。根据表达式(4)和式(5)所述条件知此方法不影响节点(n1+1,n2)和(n1,n2+1)在时间间隙t的计算。节点(n1,n2)的状态向量x(n1,n2,t)和输出向量y(n1,n2,t)的必要信息可以在时间间隙[t,t+1]内完成计算。
3 实时实现传递函数矩阵满足的约束条件
给定满足条件(4)和(5)的栅格传感器网络模型,系统实时实现的传递函数矩阵应满足如下约束条件。
设输入-输出传递函数矩阵MFD表示[9]如下:
(6)
这里矩阵NR(z1,z2,zt)和DR(z1,z2,zt)大小分别为q×p和p×p。设NR(l,m)和DR(l,m)分别表示矩阵NR(z1,z2,zt)和DR(z1,z2,zt)的第(l,m)个矩阵元素。设:
设FM模型(1)输入-输出传递函数矩阵满足条件(4)和(5)。由模型(1)知:
根据条件(4)和(5)知:
(7)
同理:
(8)
(9)
将式(7)和式(8)代入式(9)得:
(10)
传递函数矩阵H(z1,z2,zt)中矩阵元素为有理函数,节点第(l,m)个传递函数矩阵可以表示为H(l,m)。
设
(11)
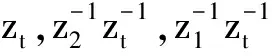
针对任意输入状态向量u(n1,n2,t)。有:
(12)
(13)
由上可知:如果实现满足条件(4)和(5)的三维FM栅格传感器网络,可推出满足系统传递函数矩阵(6)应满足的约束条件为(12)和(13)。
4 结 语
论述了三维FM状态空间模型在栅格无线传感器网络中的实现,提出了无线传感器网络研究的新方法。论述了FM模型栅格无线传感器网络系统时延问题并提出两种解决方案。针对小型传感器网络系统允许系统时延是一个很好的办法。但对于大型传感器网络系统采取修改系统矩阵方法,并通过理论推导得出该方法下系统实现零延时传输状态矩阵和传递函数矩阵应满足的条件。提出研究的新方法和得出的结论为无线传感器网络特性研究提供了依据和理论基础。
[1]AkyildizF,SuW,CayirciE.Wirelesssensornet-works:asurvey[J].ComputerNetworks,2002,38(2):393-422.
[2] 何大宇,韦铱,徐英鹏.ZigBee无线传感器网络的医疗应用研究[J].长春工业大学学报:自然科学版,2010,31(3):355-358.
[3] Verdoner. A statistical analysis of wireless connectivity in three dimensions[C]//2005 IEEE International Conference on Communications.2005:3207-3210.
[4] Huang C, Tseng Y, LO L. The coverage problem in three-demensional wireless sensor networks[C]//Proceedings of Global Telecommunications Conference. Dallas: IEEE,2004:3182-3186.
[5] Fornasini E, Marchesini G. Doubly-indexed dynamical systems: State-space models and structural properties[J]. Mathematical Systems Theory,1978,12:59-72.
[6] Dewasurendra D A, Bauer P H. Anovel approach to grid sensor networks[C]//15th IEEE International Conference on Electronics, Circuits and Systems.2008:1191-1194.
[7] Sumanasena M G B, Bauer P H. A roesser model based multidimensional systems approach for grid sensor networks[C]//43rd Asilomar Conference on Signals Systems and Computers, Pacific Grove:[s.n.],2009.
[8] 杨阳,刘智,项力领,等.栅格型无线传感器网络的状态空间建模[J].长春理工大学学报,2013,36(6):129-132.
[9] Bose N K. Multidimensional systems theory and applications[M]. 2nd. [S.l.]: Kluwer Academic Publishers,2003.
Real-time implementation of FM model in a WSN
CAO Ying-wu, LUO Xin-yu, ZHANG Bing-chuan
(College of Electronics and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China)
To ensure the sensor nodes in Wireless Sensor Network (WSN) calculate and transmit the acquired data in real time, we build the Fornasini-Marchesini (FM) model in a grid WSN and offer two solutions. The constraint conditions to meet the system transfer function matrix are mainly discussed.
Wireless Sensor Network (WSN); FM model; Transfer function matrix; grid.
2014-08-15
曹英武(1989-),男,汉族,吉林松原人,长春理工大学硕士研究生,主要从事栅格无线传感器网络(WSN)特性研究,E-mail:yingwu19891201@163.com.
TN 98; TP 29
A
1674-1374(2014)06-0668-04

