一种全息光栅曝光系统结构
撖芃芃
(中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033)
一种全息光栅曝光系统结构
撖芃芃
(中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033)
采用双透镜组的结构引入补偿镜,使工作波长和装调波长共像面。采用有限元分析方法对机械系统的设计结果进行模态分析,结果表明,该曝光系统具有较高的波前质量和系统稳定性。
全息光栅; 波前质量; 模态分析; 稳定性
0 引 言
全息光栅曝光系统是制作全息光栅的重要组成部分,其结构稳定性和可靠性决定了全息光栅的质量,具有重要的意义。
全息光栅的制作是利用光的干涉原理,在干涉场内完成的,因此,干涉场的优劣直接决定了全息光栅的质量[1-3]。用于产生干涉的光学系统一般称为曝光光学系统,其结构的稳定性在全息光栅制作过程中的作用十分明显,尤其是制作大口径全息光栅。制作大口径全息光栅的曝光光学系统具有口径较大、系统焦距较长、曝光光路较为复杂等特点,这就需要在曝光过程中提供一个较为稳定的干涉波前,同时要满足曝光光学系统波前质量的优异,只有满足这两个要求,才能制作出合格的掩模光栅。可以说全息光栅曝光光学系统直接影响到高质量全息光栅的制作,在全息光栅制作过程中起着十分关键的作用[4-6]。
文中介绍了制作全息光栅的几种光学系统,详细介绍了一种用于分振幅型全息光栅曝光系统结构设计,利用双透镜的光学设计提高了单光路的波前质量,采用补偿镜的方法解决了工作波长和装调波长不共面的问题,在结构设计上采用有限元分析方法对机械系统的设计结果进行模态分析。这些方法的采用对于制作高质量的全息光栅有着重要的作用和意义。
1 全息平面光栅制作原理
平面全息光栅制作过程原理如图1所示。
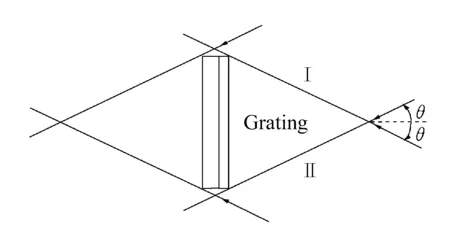
图1 全息光栅制作原理
按照干涉场电磁波原理,两束入射的相干平行光束I和II以一定的夹角2θ进入到光栅基底表面位置处时,形成具有一定规律的干涉条纹,其条纹具有明暗相间并且平行的特点,其干涉条纹间距为
式中:λ----入射光;
n----空间折射率,在空气中时n=1;
θ----两束相干光夹角的半角值。
从公式中可以看出,干涉条纹的变化是随着波长、夹角和折射率的变化而变化的。
两相干入射光束的夹角半角与干涉条纹间距关系如图2所示。
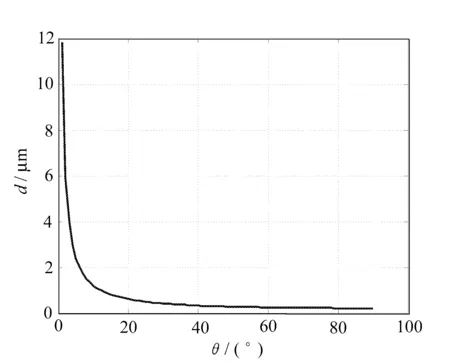
图2 两相干光束夹角之半θ与光栅常数d之间的关系图
由图2可以看出,光束夹角值与干涉条纹的间距呈现反比关系,随着入射角的增加,全息光栅的光栅常数随之减小[7-9]。
当将光栅基底和涂覆在其上的光刻胶胶层都考虑为理想平面的情况下,平面全息光栅的衍射波前质量与其干涉场干涉条纹质量有关,而干涉场干涉条纹的好坏与产生相干光的曝光光学系统的精度有关[10-12]。
2 全息平面光栅曝光光学系统设计
目前制作平面全息光栅的曝光方法大致为两种:一种为分振幅法,该类方法是利用分束镜,使同一光源出射光分为两束;另一种为分波前法,该类方法是将同一入射波面一分为二。它们的结构示意图如图3所示。
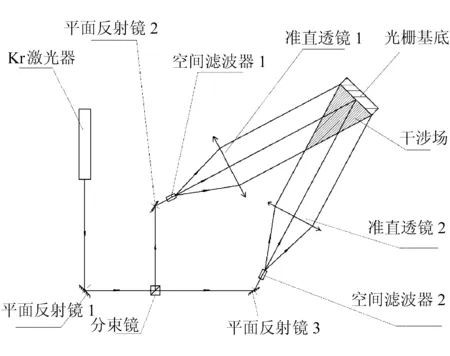
(a) 分振幅法结构

(b) 分波前法结构
拟研制的全息光栅曝光光学系统的技术指标如下:
全息光栅的尺寸:不大于Φ250mm;
全息光栅的衍射波前:优于1/4λ,λ为制作光栅使用的激光器波长。
选择分振幅法作为曝光光学系统的结构,原因是分波前法不适合制作大尺寸的平面全息光栅,如果应用分波前法就会造成在制作高刻线密度的平面全息光栅时调整反射镜尺寸过大,造成加工的难度。相比较而言,采用分振幅法更适合制作大尺寸、高刻线密度的平面光栅。
平面全息光栅曝光光学系统的设计采用双分离透镜组的形式,双分离透镜组是曝光系统的关键光学元件,它的波前质量的好坏直接决定全息光栅的质量。平面全息光栅衍射光波像差要求为λ/4,这样要求双分离透镜组所产生的波像差为λ/8。全息光栅曝光光学系统中由于有针孔(5μm)的存在使得系统在光路调整中难度较大,为了实现装调方便,在光学设计时考虑增加系统的视场角的方式提高高波前质量的范围,这样就可以使得针孔放置的要求进一步降低。曝光光学系统使用Kr+离子激光器作为光源,激光波长为λ=413.1nm,在该光路中加入了补偿镜系统,加入补偿镜系统的目的是将λ=632.8nm干涉仪产生的光与λ=413.1nm共像面,实现共像面就能对整体光学系统进行实时评价,在制作平面全息光栅时将该补偿镜系统退出。曝光光学系统的设计正是根据上述思想进行。
采用两种阿贝差较大的光学玻璃材料作为双分离透镜组中的透镜材料,选用的是石英玻璃和ZF7玻璃,光学系统的像高为1mm,也就是说在Φ1mm范围内曝光光学系统均可以产生理想波前。光学系统设计指标见表1。

表1 光学系统设计指标
光学系统结构如图4所示。
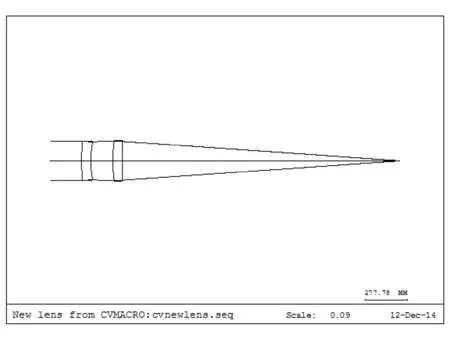
图4 光学系统结构图
光学系统的像差曲线如图5所示。

图5 光学系统像差曲线
光学系统波像差曲线如图6所示。
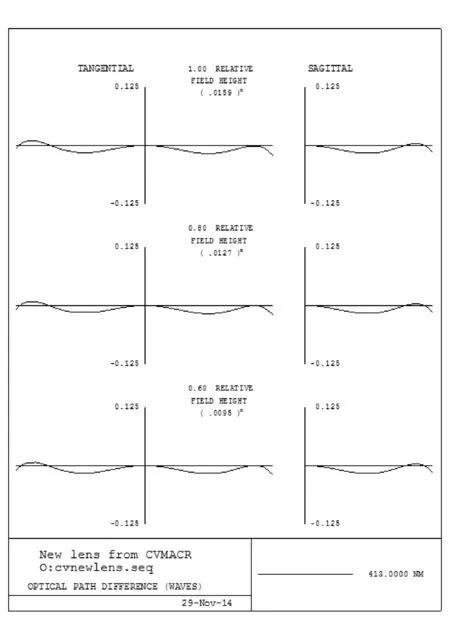
图6 光学系统波像差曲线
系统的波像差设计值为PV=0.032λ(λ=413.1 nm),满足曝光光学系统的设计要求,优于1/8λ。
加入补偿镜系统后的光学系统如图7所示,补偿镜系统采用石英玻璃,光学系统波相差曲线如图8所示。
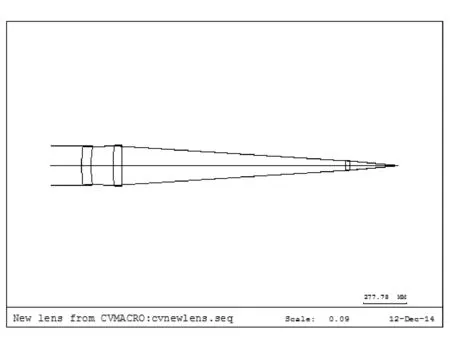
图7 加入补偿镜光学结构
加入补偿镜系统后的波像差设计值为PV=0.012λ(λ=632.8 nm)。从结果可以看出,加入补偿镜系统后曝光光学系统的整体长度没有发生变化,但在实际装调过程中十分方便,可以对波前质量进行实时检测,当用激光干涉仪(波长为632.8 nm)检测得到曝光光学系统波前质量很好时,去掉补偿镜系统,那么在413.1 nm的使用波长下仍能得到较好的波前质量,这种结构设计达到了最初的设计要求。
3 全息平面光栅曝光机械系统设计
曝光光学系统机械设计要保证曝光光学系统设计所要求的空间位置关系及公差要求,在保证设计指标的前提下,做到结构简化、重量较轻。曝光光学系统单束平行光的双分离准直镜组结构如图9所示。
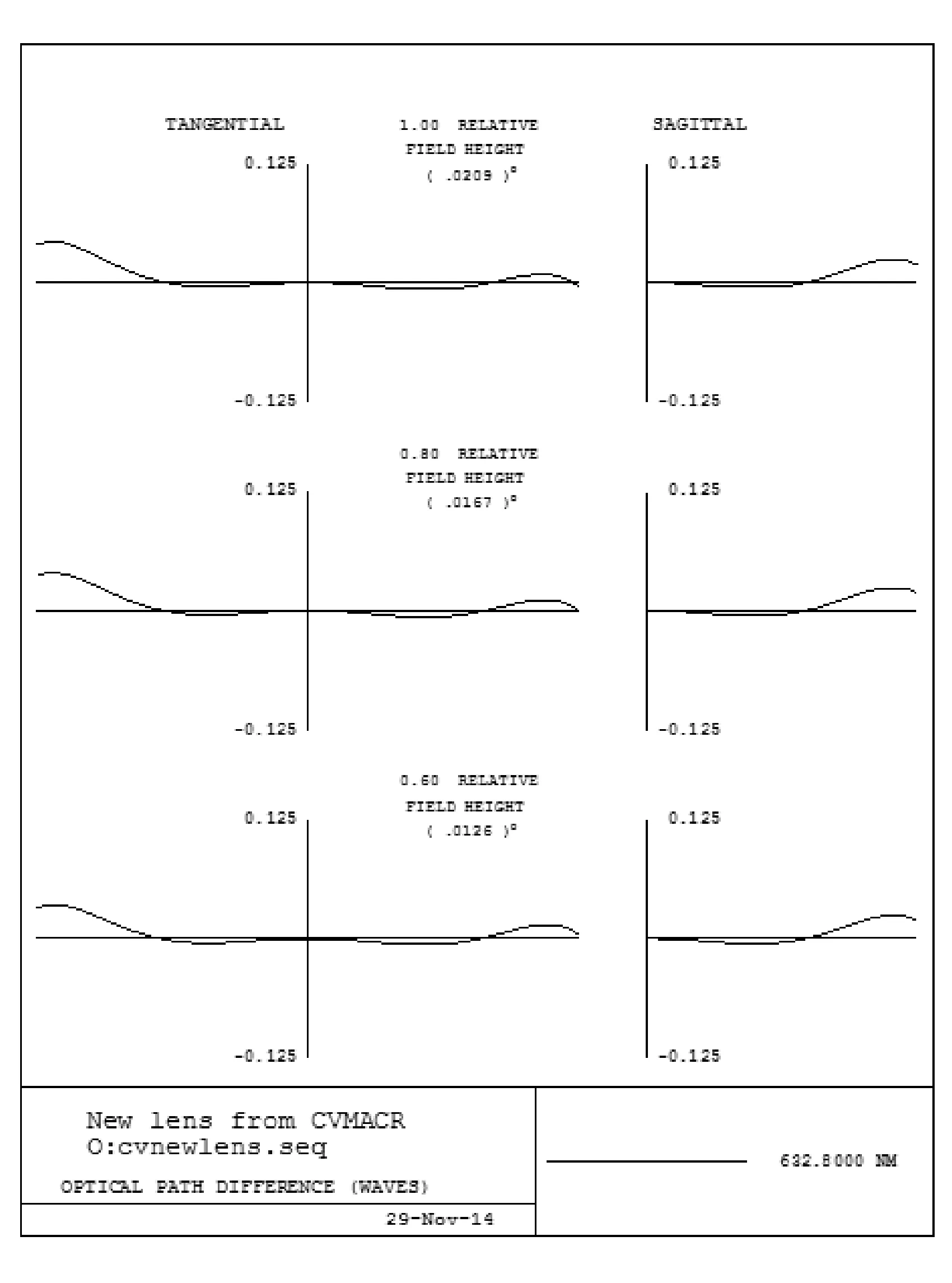
图8 加入补偿镜的光学系统图
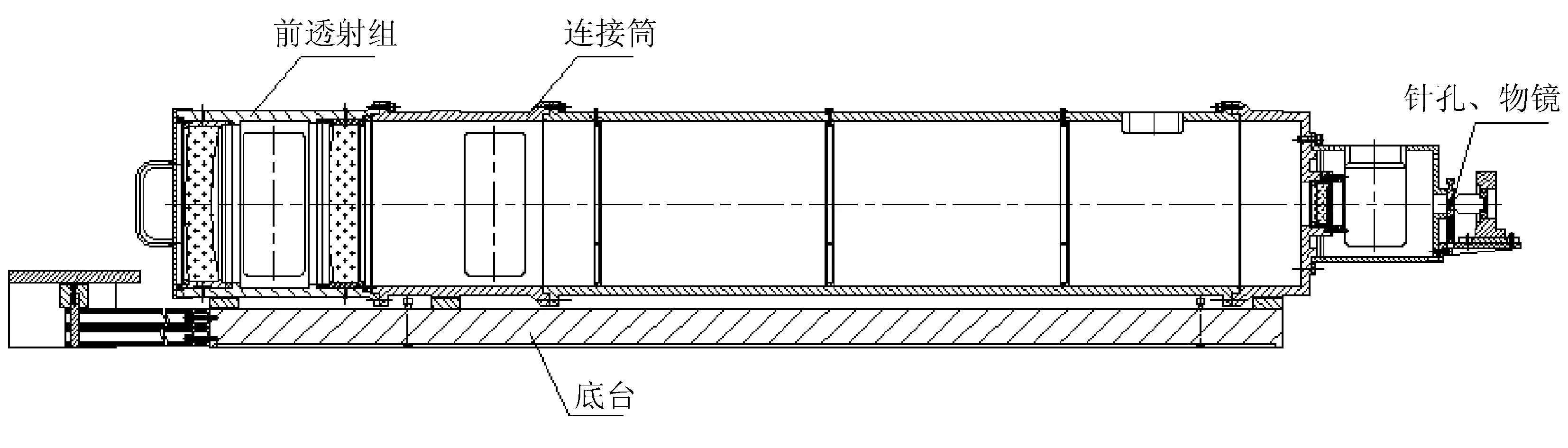
图9 单束平行光的准直镜组结构图
系统准直镜组是全息光栅曝光光学系统的重要组成部分,其稳定性直接关系到所生产光栅的质量,因此要求准直镜组具有足够的强度、刚度,同时还要具有非常高的生产和装配精度。准直镜组由以下几部分组成:
1)前透镜组;
2)连接筒;
3)针孔、物镜部分;
4)底台部分。
准直镜组结构如图10所示。

图10 准直镜组结构图
系统准直镜组系统由两块透镜组成,其中光学系统元件为圆对称回转体,透镜组采用固定环的方式,配合组件采用透镜外圆与固定环内孔配作方式,这种方式能够保证系统间隙在0.005~0.007 mm。同时外围周圈有8个直径4 mm注胶孔实现固定作用。系统的轴向固定采用压圈方式。
系统透镜组中的固定环与外镜筒在径向方向单边间隙为0.5 mm,用4个螺钉进行径向位置调整,在外筒周圈设计了8个注胶孔用以实现透镜组系统的固定。为了保证透镜组系统中各个透镜之间的同轴度不大于0.01 mm,轴向方向采用的是隔圈固定方式,通过研磨实现轴向位置要求,能够保证轴向间隔误差小于0.2 mm,角度偏差小于20″,透镜组系统固定环通过压圈螺纹处涂胶固定在外筒内部。
为了保证光学系统在整个平面全息光栅制作曝光周期内的稳定性,需要对准直镜组系统的结构设计结果进行模态分析,分析主要看其一阶和二阶谐振频率及最大重力变形情况。模态分析的目的是考察其刚度能否满足使用要求,同时考察系统在重力变形下是否满足设计指标。分析结果如图11~图14所示。
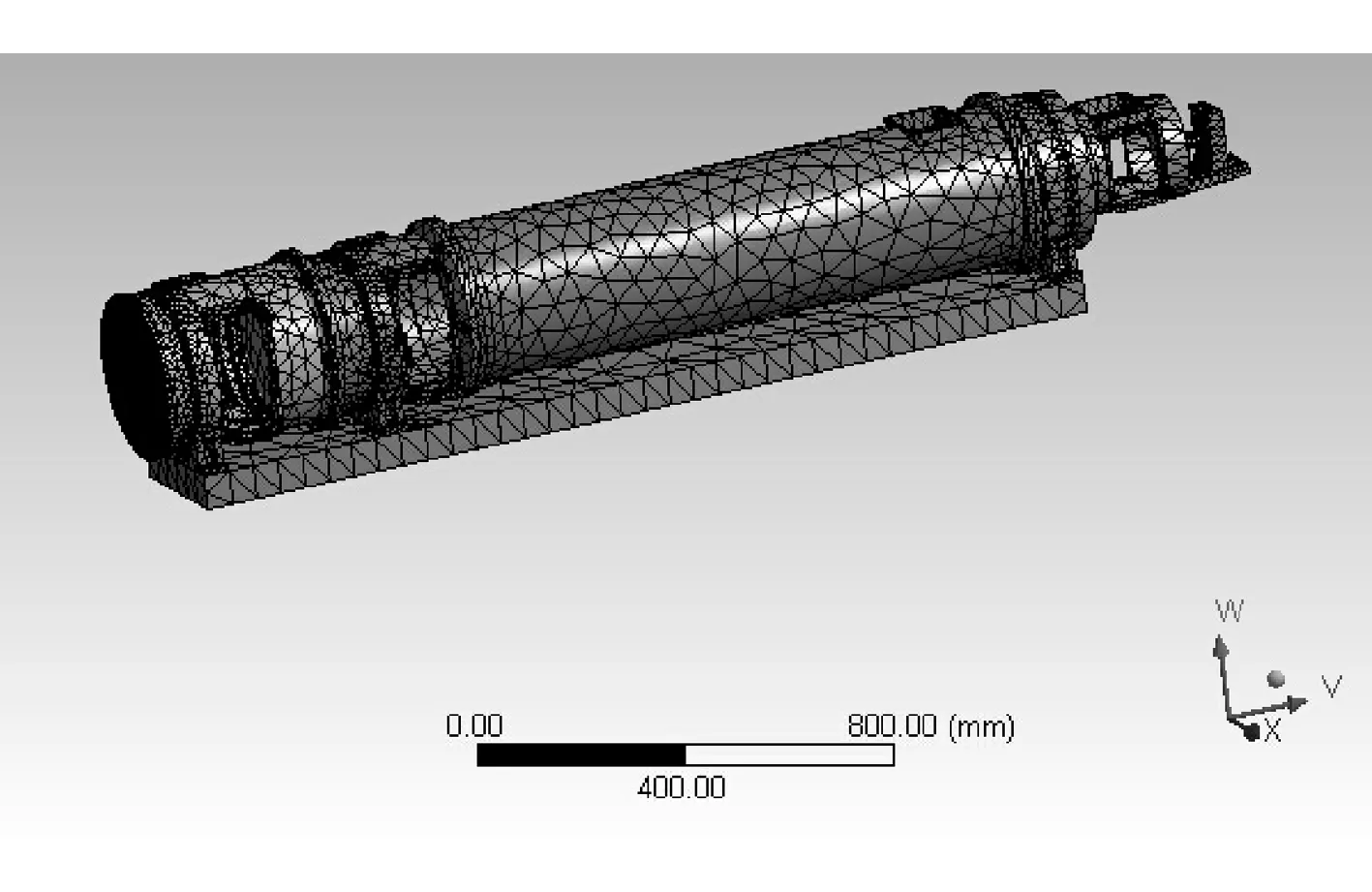
图11 系统的有限元划分

图12 系统的一阶振型

图13 系统的二阶振型

图14 系统重力变形情况
模态分析结果如下:
系统一阶振动频率:231.22 Hz;
系统二阶振动频率:285.91 Hz;
系统重力变形:3.02 μm。
从分析结果可以看出,系统的一阶和二阶振动频率较高,这意味着外来振动不会对其造成较大影响,系统的重力方向变形为3.02 μm,其值相对于1 mm的光学可调范围相比较数值较小,表面重力变形不会对曝光系统光束的波前质量产生影响,从上述的分析可以认为结构设计合理,能够保证曝光光学系统的稳定性要求。
4 结 语
为了实现高精度平面全息光栅的制作,设计了一种分振幅形式的曝光光学系统,系统利用双透镜的光学设计提高了单光路的波前质量,采用补偿镜的方法解决了工作波长和装调波长不共面的问题,在结构设计上采用有限元分析方法对机械系统的设计结果进行模态分析。这些方法的采用对于制作高质量的全息光栅有着重要的作用和意义。
[1] Chen C G, Konkola P T, Heilmann R K, et al. Image metrology and system controls for scanning beam interference lithography[J]. J. Vac. Sci. Techno1. B,2001,19(6):2335-2341.
[2] 吴娜,谭鑫,巴音贺希格,等.闪耀全息光栅离子束刻蚀工艺模拟及实验验证[J].光学精密工程,2012,20(9):1904-1912.
[3] 黄弱中,欧阳艳东.具有可变电控光栅常数的液晶光栅[J].中国光学,2012,5(3):296-301.
[4] Takeshi Namioka, Masao Seya, Hideyuki Noda. Design and performance of holographic concave gratings[J]. Japanese J. App1.Phys.,1976,15(7):1181-1197.
[5] M Koike, Y Harada, N Noda. New blazed holographic grating fabricated by using an aspherical recording with an ionetching methodi[J].Proc.SPIE,1987,815:96-101.
[6] Michel Duban. Holographic aspheric gratings printed with aberrant waves[J]. App1.Opt.,1987,26(9):4263-4273.
[7] 崔继承.O2A带高分辨率光谱测试技术研究[D]:[硕士学位论文].北京:中国科学院大学,2013:31-45.
[8] Benoit Deville, Francis Bonnemason, Jcan Flamand, et al. Holographical1y recorded, ion etched variable line space gratings[J]. Proc.SPIE,1998,3450:24-35.
[9] Ling Qing, Wu Gang, Wang Qiuping. Restricted evolution based multimodal function optimization in holographic grating design[C]//IEEE Congress on Evolutionary Computation.2005:789-794.
[10] 马森,谢芳,刘义秦,等.光纤双干涉在线绝对测量技术研究[J].仪器仪表学报,2013,34(2):268-274.
[11] Hideyuki Noda, Yoshihisa Harada, Masato Koike. Holographic grating recorded using aspheric wavefronts for a Seya-Namioka monochromator[J]. App1.Opt.,1989,28(20):4375-4380.
[12] Masato Koike, T Namioka. Optimization and evaluation of varied line spacing plane grating monochromators for third generation synchrotron radiation sources[J]. J. Electron Spectroscopy and Related Phenomena,1996,80:303-308.
A holographic grating exposure system structure
HAN Peng-peng
(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China)
Pair lens are applied in the optical system and the compensate lens are introduced to make the operation wavelength match the assemble wavelength. With finite element analysis, we design the mechanical structure and analyze the modes. The results show that holographic grating exposure system is with high quality wave-front and stability.
holographic grating; quality of wave-front; mode analysis; stability.
2014-08-28
吉林省科技发展计划项目(20126012); 吉林省科技厅青年科研基金项目(20100127)
撖芃芃(1977-),女,汉族,山西永济人,中国科学院长春光学精密机械与物理研究所副研究员,硕士,主要从事光电仪器总体设计、精密仪器设计等方向研究,E-mail:12695038@qq.com.
O 438.1
A
1674-1374(2014)06-0639-06

