假设检验的案例与应用
潘素娟, 谢 伟
(1.福建商业高等专科学校 基础部, 福建 福州 350012;2.莆田学院 数学系, 福建 莆田 351100)
假设检验的案例与应用
潘素娟1, 谢 伟2
(1.福建商业高等专科学校 基础部, 福建 福州 350012;2.莆田学院 数学系, 福建 莆田 351100)
分别介绍了参数假设检验和非参数假设检验两种方法,并通过案例分析了假设检验理论的应用,对抽样的数据进行推断分析,为以后的实际应用提供理论依据。
假设检验; 案例分析; 参数检验; 非参数检验
0 引 言
假设检验在实际生活中占有非常重要的地位,运用假设检验来解决实际问题,能避免人工判断中主观因素的影响,保证了判断结果的客观公正,符合实际。通过对实际生活案例的研究,对假设检验原理的应用有了进一步的了解。在实际生活案例分析中,讨论出模型及解决的方法,对模型作出了较完整的讨论,而这些原理对今后研究假设检验在其它方面的应用提供了丰富的资料,假设检验对于解决问题、分析实现、改进方案有着不容忽视的作用,对假设检验的学习和研究有利于科学的发展及社会的进步。
1 模型与方法
1.1基本思想
可以用小概率原理对假设检验的基本思想做出解释。小概率原理是指小概率事件在一次试验中发生的可能性几乎为零[1]。也就是说,对总体的某个假设是正确的,那么反对或者不赞同这一假设的事件X在一次试验中发生的可能性几乎为零;如果在一次试验中事件X居然发生了,那么我们有理由怀疑原假设的正确性,从而拒绝这一假设。
1.2基本步骤
1)根据实际问题的要求,充分考虑和利用已知的背景知识,提出原假设H0及备择假设H1。
2)在对想要研究的问题进行假设检验时,需要将样本统计量应用于统计推断中。在实际的问题中,检验统计量到底要选择什么样的统计量,将与参数估计一样考虑相同的因素[2]。比如,选择小样本还是大样本作为用于检验的样本,总体方差是已经知道的还是不知道的等等。检验统计量应该根据不同的情况来进行选择,并求出检验统计量的值。
3)假如原假设是正确的,我们接受了,或者原假设是错误的,我们拒绝了,这说明我们作出了正确的判断。由于假设检验是来自样本所提供的信息,从而作出推断的错误就会不可避免。有时会出现这样一种情形,原假设本来是正确的,但反而认为是错误的并且拒绝了它。这种错误发生的概率用α来说明,统计学当中把α称为显著性水平[3],也就是实际决策中本来就存在的风险。
4)按照显著性水平α与检验统计量的分布,我们能够找出拒绝域和接受域的临界位置[4],并且比较检验统计量与临界位置的值,就能够得出是接受原假设还是拒绝原假设的统计决策。
1.3常用方法
1.3.1 参数假设检验
参数假设检验方法是针对总体分布函数中的未知参数而提出的假设进行检验,常见方法有如下4种。
1.3.1.1u-检验法

来进行计算,所以其分布是标准正态分布。即
u变量就是服从标准正态分布的统计量,把应用u统计量来进行检验的方法称为u-检验法。
1.3.1.2 t-检验法
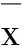
来进行计算,但是统计量t已经不服从正态分布,而是服从以n-1为自由度的t分布。即
把应用t统计量来进行检验的方法称为t-检验法。
1.3.1.3 χ2-检验法

来进行计算,此时统计量服从以n-1为自由度的χ2分布,即
把应用χ2统计量来进行检验的方法称为χ2-检验法。
1.3.1.4 F-检验法

此统计量服从F分布,即[5]:
1.3.2 非参数假设检验
非参数假设检验方法是对总体分布函数形式或类型的假设进行检验,假设母体ζ的分布函数为具有明确表达式的F(x),我们把随机变量ζ的值域分成k个互不相容的区间A1=[a0,a1),A2=[a1,a2),…,Ak=[ak-1,ak)。它们的长度并不一定是相同的。

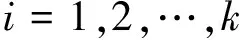
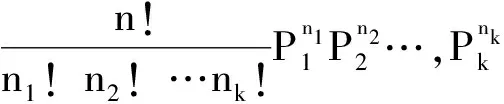

称为χ2-皮尔逊统计量[6]。能够看到,用χ2-表示这一统计量是有原因的。因为以k-1为自由度的χ2-分布是它的极限值。
为了能够把皮尔逊χ2-统计量用来作检验的统计量,必须知道它的抽样分布。先讨论k=2的简单情形。在H0成立下
其中p1+p2=1,这时,频数n1+n2=n。此时考察
令
Y1=n1-np1
Y2=n2-np2
显然
Y1+Y2=n2+n1-n(p1+p2)=0
由此可见,Y1与Y2不是线性独立,且Y1=-Y2。于是

2 案例分析
假设有6家厂商生产机床,在某一次的观测中,观测到每小时的产量见表1。
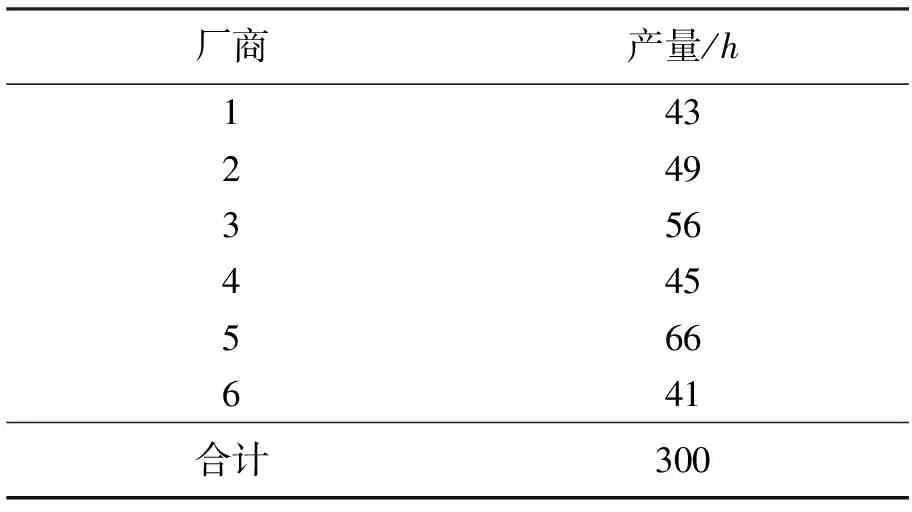
表1 6个厂商每小时的产量
试研究这6个厂商的生产能力是否具有显著性差异[7]。

先在表上计算ni-ei,然后再计算χ2统计量的值,见表2。

表2 χ2统计量的计算
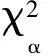
3 结 语
通过对实际生活案例的研究,对假设检验原理的应用有了进一步的了解。在实际生活案例分析中,讨论数学模型及解决的方法,并对模型作出了较完整的讨论,而这些原理为今后研究假设检验在其它方面的应用提供了丰富的资料。假设检验对于解决问题、分析实现、改进方案有着不容忽视的作用,对假设检验的学习和研究有利于科学的发展及社会的进步。
[1] 卞为梅.假设检验在质量体系认证中的应用[J].化工时刊,2004,18(4):52-55.
[2] 王金铎,唐济革,韩会英,等.假设检验在炭制品质量控制中的应用[J].炭素技术,2011,30(4):30.
[3] 刘莲花,罗文强.假设检验有意义的条件及其错误[J].湖北工业大学学报,2006,21(6):91-95.
[4] 周建男,徐风珍.假设检验方法在产品开发中的应用[J].中国质量,2006(7):77.
[5] 崔彦民,陈国良,阿拉腾图雅.假设检验的方法及应用讨论[J].内蒙古化工,2011(13):27-29.
[6] 魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,2008.
[7] 罗爱华.假设检验在生产中的应用[J].林业机械与木工设备,2010,38(4):59.
Applications of hypothesis test
PAN Su-juan1, XIE Wei2
(1.Department of Foundation, Fujian Commercial College, Fuzhou 350012, China;2.Department of Mathematics, Putian University, Putian 351100, China)
Both the parameter hypothesis test and non-parameter hypothesis test are introduced, and the cases are applied with hypothesis test theories to analyze the sampling data, which can offer some support for practices.
hypothesis test; case analysis; parameter test; non-parameter test.
2014-06-09
国家自然科学基金资助项目(11001142); 莆田学院教育教学改革资助项目(JG201112)
潘素娟(1982-),女,汉族,福建莆田人,福建商业高等专科学校副教授,硕士,主要从事概率统计与金融数学方向研究,E-mail:pansujuan309@163.com.
O 211.6; F 830.9
A
1674-1374(2014)06-0612-04

