基于可能度的区间直觉模糊数排序方法及其在决策中的应用

魏艳艳，陈子春,徐福成

(西华大学数学与计算机学院，四川 成都 610039)

1986年，保加利亚学者Atanassov[1]对模糊集进行了拓展，把仅考虑隶属度的模糊集推广到同时考虑隶属度、非隶属度和犹豫度3个方面信息的直觉模糊集[2]，它在处理模糊性和不确定性等实际问题方面更具灵活性和实用性。目前直觉模糊集理论已被广泛应用于决策、模式识别、机器学习、医疗诊断、市场预测等领域，取得了丰硕的研究成果[3-13]。由于直觉模糊集的隶属度与非隶属度有时很难用精确的数值来表达，Atanassov和Gargov又对直觉模糊集进行推广，提出了区间直觉模糊集[3],同时定义了区间直觉模糊集的一些基本运算法则。文献[4]定义了区间直觉模糊数概念，提出了区间直觉模糊加权平均算子与几何算子，并通过引入区间直觉模糊的得分函数和精确函数，给出了一种基于区间直觉模糊信息的决策方法。进一步，文献[5-6]给出了区间直觉模糊加权与有序加权平均算子及混合平均算子、加权与有序加权几何算子及混合几何算子等。在区间直觉模糊信息环境下进行多属性决策问题研究时，区间直觉模糊数的排序是前提。文献[5]基于得分函数和精确函数给出了区间直觉模糊数的一种排列方法。最近，文献[7]通过再引入隶属不确定性指标和犹豫不确定性指标，给出了区间直觉模糊数的一种全序排列方法。

直觉模糊数的得分函数与精确函数分别表达的是隶属度与非隶属度的代数和与差，它们是一个确定的值。 区间直觉模糊数的隶属度与非隶属度不是一个确定值，而是落在某个区间,反映了隶属度与非隶属度的不确定性。 当用一些确定指标值, 比如得分函数、精确函数、隶属不确定性指标和犹豫不确定性指标对区间直觉模糊数进行排序时，并不能够体现区间直觉模糊数的这种不确定性；因此，本文提出一种用区间数表达的得分函数和精确函数定义，然后基于可能度引入区间直觉模糊数的一种新的排序方法，并基于这种新的排序，给出了区间直觉模糊信息环境下的多属性决策方法。

1 区间直觉模糊集的基本知识

为了便于讨论，下面介绍区间直觉模糊集的基本定义与运算性质。

定义1[2]设X为一非空论域，一个X上的直觉模糊集A定义为

A={|x∈X}

其中：函数μA:X→[0,1]与υA:X→[0,1]满足：0≤μA(x)+υA(x)≤1,∀x∈X；μA(x)和υA(x)分别表示元素x属于直觉模糊集A的隶属度和非隶属度。πA(x)=1-μA(x)-υA(x)，通常称为x属于A的直觉模糊指标，表示x属于A的不确定程度。

Xu等在文献[8]中称(μ,υ)为直觉模糊数，其中μ∈[0,1],υ∈[0,1],μ+υ≤1，给出了直觉模糊数α=(μ,υ)的得分函数S(α)=μ-υ和精确函数H(α)=μ+υ，并利用得分函数和精确函数给出了直觉模糊数的排序方法。

由于客观事物的复杂性和不确定性，隶属度与非隶属度的值往往难以用精确的实数值来表达，而用区间数形式表达则比较适合；因此，Atanassov等[1-3]又对直觉模糊集进行了扩展，提出了区间直觉模糊概念。

定义2[3]设X为一非空论域，D[0,1]是[0,1]区间中所有闭子区间之集合。一个X上的区间直觉模糊集A定义为

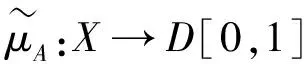
为了利用方便，徐泽水等在文献[4-6]中称序对([a,b],[c,d])是所谓的区间直觉模糊数，其中[a,b]⊂[0,1]，[c,d]⊂[0,1],b+d≤1，并给出了区间直觉模糊数的运算法则与集成方法，其中集成方法有区间直觉模糊加权与有序加权算术平均算子及混合平均算子、加权与有序加权几何算子及混合几何算子等，本文主要用到区间直觉模糊数的加权平均算子和加权几何算子。

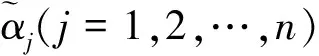
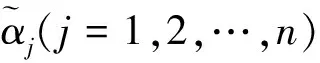
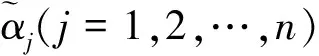
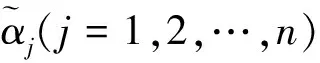
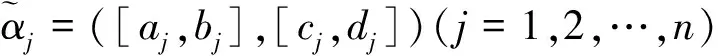
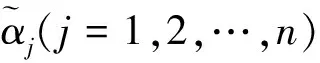
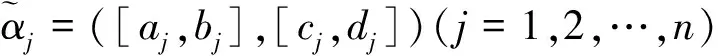
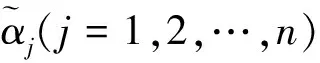
为了对区间直觉模糊数进行比较，以便得到满足要求的最佳方案，徐泽水等在文献[4]中给出区间直觉模糊数的得分函数和精确函数的定义。

2 区间直觉模糊数的得分函数与精确函数

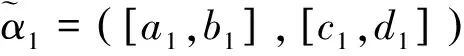
其中，μ是R×R上的面积测度。

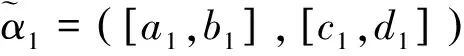
根据定义，容易得到：

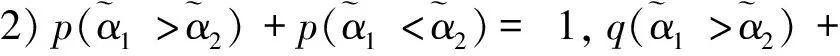
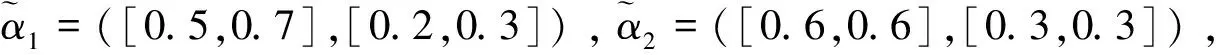
基于得分函数可能度和精确函数可能度，下面给出2个区间直觉模糊数的排序方法。

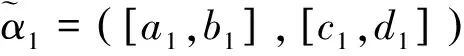
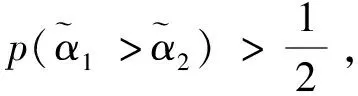
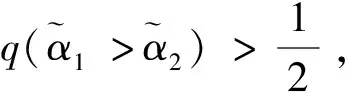
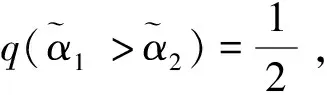
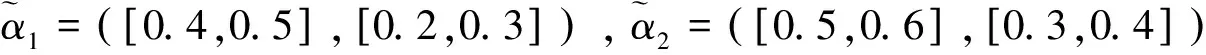
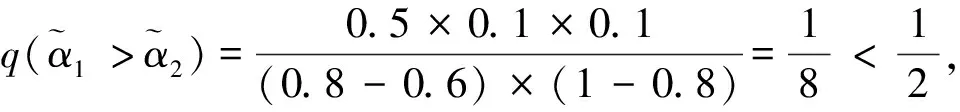
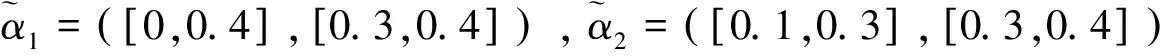
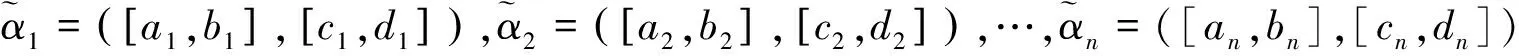
其中pij≥0,pij+pji=1,pii=0.5,i,j=1,2,…,n。称p是得分函数互补矩阵。

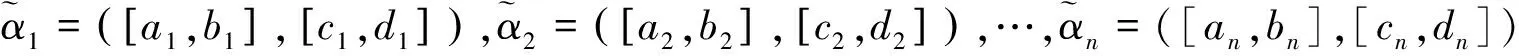
其中：qij≥0,qij+qji=1,qii=0.5,i,j=1,2,…,n。称q是精确函数互补矩阵。

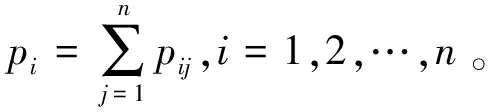
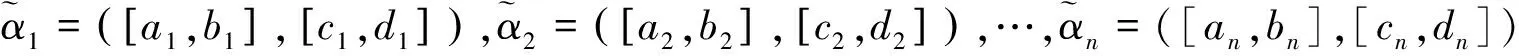
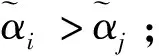
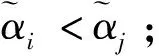
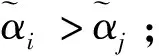
运用定义14给出的区间直觉模糊数的排序方法，下面给出一种基于加权平均算子和加权几何算子下的区间直觉模糊多属性决策法，具体如下：

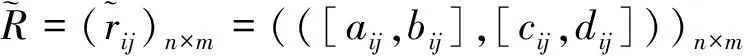
步骤1 利用区间直觉模糊数的加权平均算子

或加权几何算子

3 实例分析

下面利用一个投资决策问题来说明我们提出的方法的可行性和有效性。

假设一个基金经理在一个财富管理公司评估4个投资机会，X={x1,x2,x3,x4}。选择每种投资机会都有4个属性：冒险(a1)、增长(a2)、政治问题(a3)和环境因素(a4)，基金经理提供了各投资机会在各属性下的评估信息，经过统计处理后可表示为区间直觉模糊数，决策矩阵[9]如下

这个矩阵中的每个元素都是一个区间直觉模糊数，代表了基金经理评估一种替代方案的隶属度和非隶属度。例如，矩阵的左上角的元素([0.42,0.48],[0.4,0.5])反映了基金经理认为在冒险(a1)远景下选择投资x1是优越的概率为42%～48%，不优越程度在40%～50%之间。假设基金经理提供出了各属性的权重信息：ω1=0.150 0(冒险)，ω2=0.175 0(增长)，ω3=0.375 0(政治问题)，ω4=0.300 0(环境因素)。下面根据本文所给出的区间直觉模糊信息环境下的多属性决策方法计算出4种投资机会的排序。

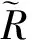
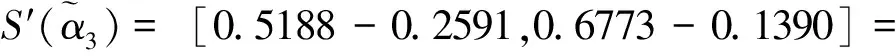
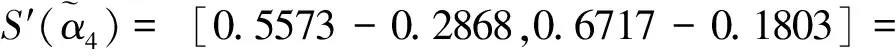
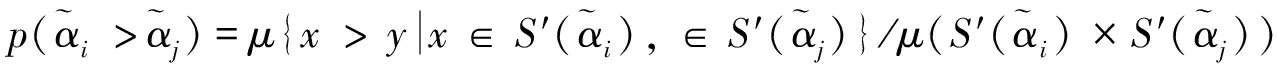
步骤4求得

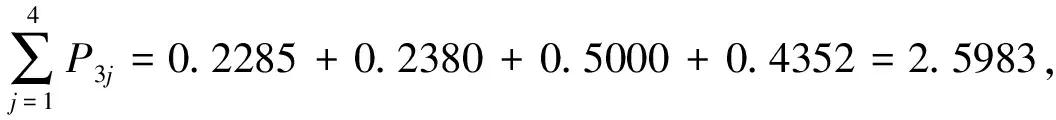
因此最终排序为x3≻x4≻x2≻x1。

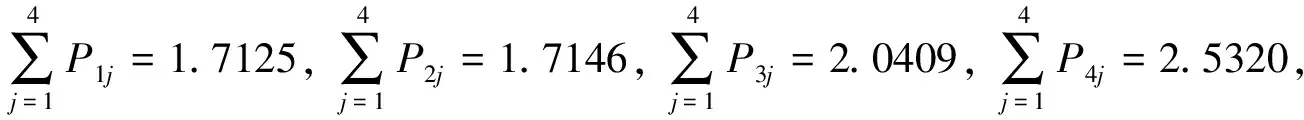
对于这个投资问题，利用加权平均算子得到的排序为x3≻x4≻x2≻x1，利用几何算子得到的排序为x4≻x3≻x2≻x1，因此总的来说x3和x4是首要选择，x1和x2作为次要选择。

4 结束语

本文对模糊数问题进行了研究，为区间直觉模糊数提出了一种新的排序方法，该方法利用得分函数区间和精确函数区间求出得分函数可能度和精确函数可能度，然后对区间直觉模糊数进行排序。本文还给出了基于直觉模糊信息的一种新的决策方法，将区间直觉模糊决策矩阵转化为区间数的决策矩阵，再运用得分函数区间的可能度求和得到排序。

[1]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems, 1986，20: 87-96.

[2]Atanassov K.Intuitionistic Fuzzy Sets: Theory and Applications[M]. Heidelberg: Physica-Verlag, 1999.

[3]Atanassov K,Gargov G.Interval-valued Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems, 1989,31(3): 343-349.

[4]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策，2007, 22(2): 215-219.

[5]徐泽水，陈剑.一种基于区间直觉判断矩阵的群决策方法[J].系统工程理论与实践，2007, 27(4): 126-133.

[6]Xu Z S,Chen J.On Geometric Aggregation over Interval-valued Intuitionistic Fuzzy Information[C]//In Proceedings of the fourth international conference on fuzzy systems and knowledge discovery. Washington: IEEE Computer Society Press,2007: 466-471.

[7]Wang Z,Li K W, Wang W.An Approach to Multiattribute Decision Making with Interval-valued Intuitionistic Fuzzy Assessments and Incomplete Weights[J]. Information Sciencesg，2009,179: 3026-3040.

[8]Xu Z S, Yager R.Some Geometric Aggregations Based on Intuitionistic Fuzzy Sets[J]. International Journal of General Systems, 2006,35: 417-413.

[9]Herrera F,Herrera-Viedma E.Linguistic Decision Analysis: Steps for Solving Decision Problems under Linguistic Information[J].Fuzzy Sets and Systems,2000,115:67-82.

[10]Hsu S C, Wang T C.Solving Multi-criteria Decision Making with Incomplete Linguistic Preference Relations[J].Expert Systems with Applications,2011, 38:10882-10888.

[11]J W ,J B L.Some Programming Models to Derive Priority Weights from Additive Interval Fuzzy Preference Relation[J].Knowledge-Based Systems,2012,27:69-77.

[12]Z P.Rational Decision MakingModels with Incomplete Weight Informationfor Production Line Assessment[J].Information Sciences,2013,222:696-716.

[13]J W.Robust Optimization Analysis for Multiple Attribute Decision Making Problems with Imprecise Information[J].Annals of Operations Research,2012, 197:109-122.