2014年新疆于田MS7.3地震矩心矩张量快速测定

赵旭 黄志斌 陈宏峰 赵博 杜广宝

中国地震台网中心，北京市西城区三里河南横街5号 100045

0 引言

2014年2月12日17时19分新疆于田县发生MS7.3地震(简称于田地震)。该地震发生在民丰县西南约110 km、于田县东南约112 km处，处于西昆仑造山带内。震中位于昆仑山脉北麓的阿羌乡偏远山区，地广人稀，但地震仍造成多处房屋桥梁受损，两千多只牲畜死亡。该地震发生在距印度板块和欧亚板块碰撞带数百千米的青藏高原北缘，位于中强地震较为活跃的EN向阿尔金断裂带上，地质构造较为复杂(图1)。

地震发生后，如何在更短的时间内获知矩心时间、矩心位置、标量地震矩以及断层面几何参数等地震工作者们所关心的重要震源信息已成为国内外地震学家普遍关注的问题。这些信息能直观地反映地震破裂面几何形状和运动学特征，对大地震本身的研究(Duputel et al，2012a)、地震灾害快速评估(Dreger et al，2005)、海啸预警(Kanamori et al，2008)及震后应力分布研究(Parsons et al，2008)等都有重要的意义。为此，赵旭等(2014a)研制了全球强震矩心矩张量自动反演系统。该系统采用全球地震台网宽频带台站记录的远震波形，并基于Kanamori等(2008)提出的基于W震相测定矩心矩张量的方法。通过离线自动测定的2008年1月～2013年7月全球140个地震(MW6.5～9.0)的矩心矩张量与美国哥伦比亚大学Global CMT进行了比较，评估结果表明此系统能实现25～40min自动准确测定全球MW6.5～9.0地震的矩张量。

图1 地震震中位置及周围断层分布

W震相(W phase)是在S波之前到达的一种较明显的长周期波(100～1000s)，最早于1992年日本记录的尼加拉瓜海啸地震的位移波形中被辨识出(Kanamori，1993)。根据地震射线理论，在选定初至P波开始至15Δ秒(Δ表示震中距，单位为度)时窗中，W震相所携带的能量可解释为P、PP、SP和S等多个震相的叠加。本文使用的W震相测定地震矩张量法采用全球一维速度模型PREM，基于简振正型叠加法计算理论波形。

为进一步提高中国大陆中强地震(MW≥5.3)矩张量测定的时效性，赵旭等(2014a)使用最新的构建了虚拟中国地震台网记录的近震波形(震中距小于12°)，采用改进的W震相技术，开发了中国大陆中强震自动矩张量测定系统。此系统自2013年7月开始在中国地震台网中心上线试运行，其测定结果一般在震后约15min内得到。此次于田地震再次检验并证明了系统的稳定性，自动测定结果在震后约9min得到，且与Global CMT工作组给出的结果基本一致。

本文基于中国大陆中强震自动矩张量测定系统，采用虚拟中国地震台网记录的近震波形，反演于田地震的矩张量，给出于田地震基于点源的震源机制解，并探讨了自动矩张量测定系统在未来地震灾情预判中的作用。

1 数据

为了尽可能地减少台站分布不均匀对国内地震矩张量测定结果的影响，通过对多个历史震例理论波形和实际观测记录进行比较分析，最终从中国地震台网中选取211个记录质量较高的台站，联合全球地震台网II、IU等，建立了虚拟中国地震台网。考虑到速度型地震计的幅频特性以及强震激发的地震波包含主要能量的频段范围，选取的国内台站地震计类型多为JCZ-1、JCZ-1T、CTS-1、CMG-3ESPC或 BBVS-120型。国际台地震计类型多为 STS-1或STS-2型。

利用虚拟中国地震台网记录的于田地震近震波形(震中距4°～12°)，数据预处理中采用新疆地震台网正式目录给出的于田地震基本参数:发震时刻为北京时间2014年2月12日 17:19:48.19，震中位置 36.123°N、82.499°E，震源深度 10 km(http://10.5.202.22/bianmu/validate.jsp，查询时间2014年2月26日)。

数据预处理主要步骤:①控制波形质量。考虑台站均匀覆盖情况和波形记录信噪比，舍去信噪比不高和断点等“坏”波形;② 时间域反卷积。将原始的速度地震记录转化为位移记录;③采用4阶巴特沃斯(Butterworth)滤波器进行带通滤波。滤波频段120～500s;④选用初至P波后180s为W震相时间窗。

2 方法

2.1 反演方法

W震相矩张量反演采用的技术思路类似于Dziewonski等(1981)和Ekström等(2005)提出的标准矩心矩张量(Centroid moment tensor)反演方法，但两种方法有4个方面的不同:①选用地震波时间窗的不同;②W震相矩张量反演使用长周期地震波形;③前者采用时间域反卷积方法，能对时间序列每个抽样点进行实时处理，使得W震相可在限幅记录中无失真恢复，从而使该方法可充分利用强震近震(震中距3°～12°)波形。而后者主要使用频率域反卷积方法提取位移波形;④确定矩心水平位置和矩心深度的反演算法不同。

在W震相反演中未知震源参数向量m可由下式表示

其中，地震矩张量 f=［Mrr，Mpp，Mtt，Mrp，Mrt，Mpt］T;矩心时空坐标 ηc=［θc，φc，hc，τc］T，其中 θc，φc，hc，τc分别表示矩心余纬度、矩心经度、矩心深度以及矩心时间，T表示转置运算符。

为了确定最佳的矩心时空坐标ηc，可通过网格搜索的方法使下式定义的误差函数最小

其中，向量sw表示W震相的理论波形;向量dw为W震相的实际观测。

由于使用近震台站记录的W震相在测定强震震源参数方面具有以下优势:①W震相传播速度明显高于面波，因此相比于传统的面波波形反演方法，一般在震后15min可完成对震源参数的测定，更适合大震快速响应;②W震相主要在地幔中传播，浅层大陆地壳和洋壳结构的强烈不均匀性对W震相的影响不大。因此，该方法逐渐被美国国家地震信息中心、美国太平洋海啸警报中心、日本气象厅等国外多家科学机构所使用(Hayes et al，2009;Duputel et al，2012b)。

2.2 自动处理流程

第1步，采用新疆地震台网正式给出的于田地震震源位置和震级M，基于Kanamori等(2008)的方法，可通过震级M估算出矩心时间偏移td，反演得到初步矩张量解。

第2步，在假定上述震源位置为矩心位置的前提条件下，基于一维网格搜索在矩心时间偏移td解空间中求出最佳s解，使误差函数χ(m)最小。使用最佳解td(图2)，再次迭代计算，修订第1步求得的矩张量解。

第3步，在满足遴选后波形道数N≥15和台站方位间隙角γ≤270°的条件下，开始时水平向搜索间隔为0.4°，尔后在局部最小值附近进一步细化网格为0.2°、0.1°。在深度向搜索间隔一般为2 km。基于三维网格搜索，使误差函数χ(m)最小，求出最佳的矩心水平位置和矩心深度。使用优化的矩心水平位置和矩心深度(图3)再次计算，得到最佳矩张量解(图1)。

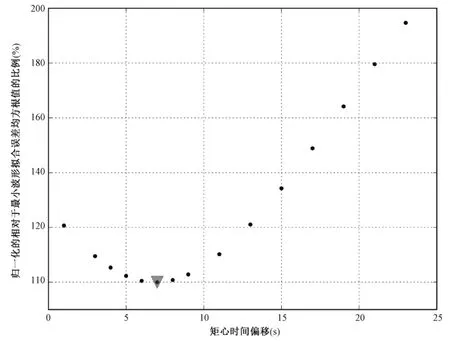
图2 通过一维网格搜索求出矩心时间偏移td最佳解

3 结果分析

在于田地震的地震矩张量反演中，使用了距于田地震12°范围内共20道波形(图4)。台站覆盖间隙角约108°。为了使台站覆盖均匀，增加了位于中国境内及其周边4个国际台站记录的高质量长周期垂直向波形(IC_WMQ，IC_LSA，II_AAK，IU_MAKZ)。

经第3步计算后，获得实际观测波形与理论波形拟合最优的矩张量(表1)。图4给出实际观测波形和理论波形的对比。由图4可见，大多数台站的实际观测波形与理论波形拟合较好，波形拟合误差均方根值(RMS)为0.017mm，略小于Global CMT给出的矩张量模拟理论波形与实际观测波形拟含误差均方根值0.019mm。需要指出的是，通过比较4个国际台站的整个波形拟合情况发现，基于本文研究的点源模型，能较好地模拟未参与反演的面波部分，说明本文的结果是可信的。

图3 网格搜索获得的矩心水平位置最佳解

表1 于田地震震源参数对比

由表1可知，于田地震的总标量地震矩M0为3.05×1019N·m，换算成矩震级约MW6.92，最佳双力偶解的节面 I和节面Ⅱ(走向/倾角/滑动角)为 243°/70°/-18°、339°/73°/-159°。补偿线性矢量偶极(CLVD)根据 λ2/(|λ1|，|λ3|)计算得到，其中本征值 λ1＞ λ2＞λ3，约23.8%，说明除具有双力偶的剪切位错外，还含有较多的非双力偶成分。节面I的走向、倾角与震中附近阿尔金断裂的走向、倾角最为接近(图1)，因此认定节面I为发震断层面，判定于田地震为一次左旋走滑为主兼有少量正倾滑分量的事件。

通过网格搜索最佳波形拟合的矩心时间偏移td约为7s(图2)。假设矩心时间偏移td能表征震源破裂持续时间(Rupture duration)的(Kanamori et al，2008)，则推断震源破裂时大部分能量释放的持续时间约14s。矩心震中位置(36.123°N，82.623°E，图3)较破裂起始点(36.123°N，82.499°E)在水平方向往东偏移约13km，说明能量释放集中区中心位于破裂起始点以东约13km。矩心深度约10km，同破裂起始点深度一致。

图4 每道实际观测波形(黑线)和理论波形(红线)的对比

4 讨论与结论

本文采用虚拟中国地震台网记录的近震波形，基于W震相技术的矩张量测定系统，成功反演了于田地震的矩心矩张量解。结果表明，于田地震发震断层面参数分别为走向243°/倾角70°/滑动角-18°，补偿线性矢量偶极(CLVD)约23.8%，为一次左旋走滑为主兼少量正断倾滑分量的事件。该结果同哥伦比亚大学Global CMT工作组根据远场体波和面波给出的断层面参数基本一致，也同王卫民等①王卫民等，2014，2014年2月12日新疆于田7.3级地震震源破裂过程反演初步结果(http://www.igg.cas.cn/xwzx/yjcg/201402/t20140214_4032524.html.)基于远场体波反演获得点源模型的震源机制解(走向240.0°/倾角71.9°/滑动角-2.2°)相吻合。王卫民等①根据破裂过程的反演结果认为，于田地震是左旋走滑为主并具有正倾滑分量的事件，与本文得出的对于田地震断错性质的认识相同。

自动测定地震矩张量能在震后第一时间内获取地震矩心时间、矩心位置、标量地震矩以及断层面几何参数等地震工作者们所关心的重要震源信息，对地震灾情预判具有重要作用。其应用价值体现在以下5个方面:①快速测定大震(MW≥8.5)的矩震级，可避免因采用其他震级标度出现的震级完全饱和而低估震级的问题，更好地服务于大震速报(Hanks et al，1999;陈运泰等，2005);②用于甄别隐伏断裂的几何产状，快速确定地震破裂方向及估算破裂尺度大小等(Cesca et al，2011;赵旭等，2014b);③作为基础资料，可用以修正震源模型，计算准确的地震动图(Dreger et al，2005);④通过确定震级的大小、震源破裂方式及震源深度等，用于地震海啸预警(Kanamori et al，2008);⑤计算地震库仑破裂静应力变化，判定未来余震趋势(Parsons et al，2008)。

基于近震波形的中国大陆中强震(MW≥5.3)自动矩张量测定系统，适合于中强震甚至大震(MW≥7.5)的矩张量反演(Duputel et al，2012b;赵旭等，2014a)，且时效性较强。由于使用时间域反卷积方法能对时间序列每个抽样点进行实时处理，使得W震相可在限幅记录中无失真恢复，可充分使用强震、近震(震中距3°～12°)的宽频带波形，而不必考虑收集远场波形(震中距30°～90°)等待时间。本文基于此系统，采用虚拟中国地震台网记录的近震波形(震中距4°～12°)成功反演了于田地震的矩心矩张量，再次证明了系统的稳定性和适用性。未来系统正式运行后，其测定的震源关键信息，不仅是大地震研究的基础资料，而且将在地震灾害的快速评估、海啸预警及震后应力分布研究等方面发挥重要作用。

致谢：衷心感谢周龙泉研究员在本文成稿过程中提出的宝贵建议。中国地震台网中心地震台网部数据管理组提供了高质量数据波形。全球台网数据从IRIS DMC下载，在此一并表示感谢!