利用华北地区承压井水位资料反演含水层体应变
杨柳 马建英 曹井泉 邵永新 刘文兵2,
1)天津市地震局,天津市河西区友谊路19号 300201
2)中国地震局地球物理研究所,北京100081
0 引言
有研究认为,承压井水位的变化反映了含水层孔隙压力的变化,而含水层孔隙压力的变化与含水层所受的压力状态有密切的关系。因此,观测并记录钻井内水位的变化,是测量地下深部弹性应力变化的方法之一(黄辅琼等,2004)。为了寻求承压井水位与含水层应力应变的关系,国内外学者开展了大量工作。Narasimhan等(1984)给出了体应变与固体潮引起的水位变化之间的定量关系式。黄辅琼等(2004)利用华北地区40多口深井水位动态观测资料,定性地分析了大华北地区的构造应力场状态。张昭栋等(1999)利用含水层参数、固体潮效应和气压效应等3种方法反演含水层应力应变,并进行了分析比较。孙小龙等(2011)利用华北地区63口井的水位变化和井含水层水文地质参数资料,反演出华北地区构造应力场变化图像。
由于利用含水层的水文地质参数和水位气压效应来反演含水层应力应变,是建立在水平层状承压含水层这种平面假设的基础上的,并且在选取水文地质参数时一般取其可能值或平均值,容易使计算结果出现误差(张昭栋等,1999)。因此,在借鉴前人研究成果的基础上,本文筛选了华北地区反应固体潮较好的承压井水位资料,利用井水位的固体潮效应来反演华北地区现有承压井孔的含水层体应变。该方法不但结合了含水层的实际情况而且反映了体积力产生的应力应变,计算结果更为可靠。
1 研究方法
研究表明,两个因素可引起承压井水头的变化:承压井含水层内水量的变化和含水层所受的应力应变的变化。对于封闭性较差的含水层主要是第一种原因,例如降雨或同层抽水引起含水层水量发生变化;对于封闭性良好的含水层主要是第二种原因。对于完全封闭的含水层,若只有一口井,其水头的变化只取决于含水层所受的应力应变的变化。实际上由于含水层的封闭性不可能是完全理想的,所以水井含水层压力水头的变化基本上都是两种原因的综合(张昭栋等,1999)。
此处,本文仅考虑第二种理想的封闭性良好的含水层。根据孔隙弹性介质理论,作用于含水层某一平面上的荷载分别由固体颗粒与颗粒间的孔隙流体共同承担。由此,可以得到井水位变化与体应变之间的关系式(Rhoads et al,1979)
其中,ρ为含水层内水的密度;g为地球表面的重力加速度;n为含水层的孔隙度;Em和Ew分别为岩石固体颗粒和孔隙流体的体积模量;dh为含水层井水位的变化量;ΔΘ为体应变量;δ为潮汐因子,表示单位体应变引起的井水位变化。
由式(1)可以看出,对于封闭性较好的深层承压井来说,通过计算井孔水位的潮汐因子和水位变化量,就可以求得该井的含水层体应变的变化量。
2 资料的选取
“九五”、“十五”期间数字观测技术在全国前兆观测网络中得到了广泛的应用,华北地区的井水位观测已经由模拟观测逐步改造为以数字观测为主的观测网络。数字化改造使得前兆资料的观测、传输高度自动化,观测数据的采样密度和灵敏度也大幅提高(田山等,2009)。目前,井水位数字化观测已全部实现了分钟计值采样,部分测项的采样密度达到以秒计值,这为提取水位固体潮的潮汐因子提供了数据保障。
本文收集了2003年以来华北地区(34°~42.5°N,111°~123°E)反应固体潮的承压井的基础资料和水位、气压的整点值数据,并筛选出数据质量较好的33口井孔的水位资料。观测井主要分布在河北、北京、天津、辽宁、内蒙、山东、河南和山西等8个地区(图1)。
3 潮汐因子的计算
计算潮汐因子,首先要提取研究井孔水位的固体潮信息。水位波动的影响因素主要有固体潮、地震波、气压、降雨、海潮等,对于封闭的含水层,这些影响因素是通过对含水层的作用导致其压缩或膨胀,从而引起水头的变化(史浙明等,2012)。由于水位固体潮的变化周期约为12~25h,而地震波以及降雨荷载与固体潮的周期相差较大,且海潮负荷仅对距离海洋较近区域的井水位产生明显的影响。因此,利用地下水水位的固体潮反演含水层体应变时,我们只排除气压的影响,并对受海潮影响较大区域的井孔排除了海潮负荷,从而得到33口承压水位井的潮汐因子。

图1 华北地区33口数字化水位井分布
3.1 数据的预处理
首先对观测资料进行预处理,消除因观测条件改变或其他干扰造成的数据突跳、阶变等情况,然后应用3次样条插值法将观测仪器故障等原因造成的缺数补齐。图2(b)为河北无极井预处理后的整点值水位数据曲线。
3.2 去除气压效应
在各种影响因素中,气压对地下水位观测的影响较为关键(万永芳等,2009;刘学领等,2010)。目前,在去除地下水位观测气压效应的分析研究中,较为常用的方法有线性回归、多元回归等。回归方法的优点是方法成熟、易于计算,但也存在一些不足。比如在计算过程中,主要是通过相关分析求取1个气压系数,进而去除气压的影响,并没有考虑气压随时间的变化对水位的影响;此外,井水位的气压效应普遍存在时间滞后现象(赵丹等,2013),而上述回归法并没有考虑这种影响。应用卷积回归法来去除气压效应就可解决上述问题,该方法是通过调整最大响应时间以生成配对的水位和气压观测值的最佳阶跃响应函数(气压响应函数),再由气压响应函数计算出修正后的水位变化。BETCO程序(Toll et al,2007)应用卷积回归法实现了估计气压和井水位变化之间的时间滞后效应,并可以自动去除气压对观测水位的影响(图2)。
3.3 去除长周期趋势和滤波
由于所要提取的固体潮周期为12~25h,因此为了得到更清晰的这种短周期的水位变化曲线,首先要去除水位的长周期趋势变化。本文采用按月分段的一般多项式拟合方法来去除水位的趋势项,图3(a)为去除趋势后的水位变化曲线。

图2 2013年1月1~31日无极井气压和水位

图3 2013年1月1日~31日无极井水位
去除水位长周期趋势变化后,水位曲线中仍然存在较短周期的波动变化,因此还需要进行滤波处理。对水位整点值做48h的滑动均值并滤波,无极井水位滤波后的曲线(图3(c))与理论曲线(图3(d))相比潮汐的变化形态已经比较一致。
3.4 计算潮汐因子
井孔水位的固体潮可以分离成363个分波。调和分析结果表明,在这些分波中最主要的分波为半日波M2波,在水位固体潮振幅中,该波所占的比例达30% ~40%;其次是K1、S2、O1和N2等波(张国民等,2001)。因此,本文采用Venedikov调和分析方法,利用2008年1月~2012年12月的水位数据计算了33口水位井的M2波潮汐因子。
3.5 剔除海潮负荷
由于海潮负荷的体应变响应与距离有密切关系,观测点距海岸线30km以内,体应变响应随着距离的减小而迅速增大(曹井泉等,2010);在30~90km范围内,随着距离的增大,体应变响应逐渐减小;超过100km时,体应变响应明显减弱。因此,本文选取了距离海岸线100km以内的水位井做剔除海潮负荷的计算,包括宝坻、张道口、静海、玉田、沈家台、鲁02、鲁07等井。
本文应用Schwiderski全球海潮模型,采用积分格林函数方法计算上述7口承压井水位M2潮汐波的应变负荷潮,在计算水位M2潮汐波的振幅和相位的基础上,进行海潮负荷改正。首先,以38.70°N、118.40°E点为海潮负荷点,根据李艳芸等(2006)利用Coherens模型给出的渤海海潮图,计算出7口水位观测井的M2波海潮负荷矢量振幅和相位滞后。然后结合之前的水位调和分析结果,计算出观测残差矢量和剩余残差矢量,最终求出经海潮负荷改正后的潮汐因子和相位差,渤海海潮图及具体的计算步骤和公式见李艳芸等(2006)及曹井泉等(2010)文献。
在此选取了2012年1月1日~3月31日共3个月的数据进行海潮负荷改正的计算,表1显示了海潮负荷改正前、后所得到的水位M2波潮汐因子和相位差的计算结果。由表1可见,距离海岸线50km以内的鲁02井和张道口井,海潮负荷改正前、后的M2潮汐因子计算结果相差较大;其他井孔的计算结果随着距离的增大,差距在逐渐变小。而且经过海潮改正,这几口井的相位差均表现为负值且数值离散度较小,说明计算取得了较好的海潮负荷改正效果。

表1 水位M2潮汐波海潮负荷改正结果
4 水位趋势变化的提取
分析33口井的原始观测曲线图,水位的变化可以分为趋势性上升、趋势性下降和起伏波动等3种类型,有的井水位还会在趋势性变化上叠加年周期变化(图4)。在利用井水位反演含水层体应变时,水位下降表明含水层压性减弱,张性增强;水位上升表明含水层张性减弱,压性增强。因此,承压井水位的变化决定了井所在区域应力场的变化。经过统计,本文研究的水位井中呈现下降变化的有24口,占总数的73%。如果这种变化完全是由于含水层应力状态引起的,那么说明整个研究区域处于长期拉张状态,这与研究区域的应力应变背景并不相符。进一步分析这24口井的呈下降趋势的水位资料,其中16口井的水位呈线性下降特征,且幅度较大,这些井主要集中在北京、河北、天津、山西和鲁豫交界等地区。本文从“中国水文信息网”①水利部水文局,2003~2010,我国北方平原区地下水通报(中国水文信息网)搜集了这几个区域的年降雨量数据(图5),由图5可见,年降雨量曲线并没有持续下降,反而是呈现一种起伏性上升,因此井孔水位的持续下降并不是由降雨量变化引起的。
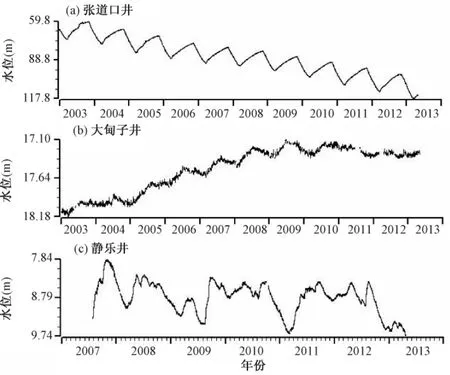
图4 不同趋势类型水位变化曲线
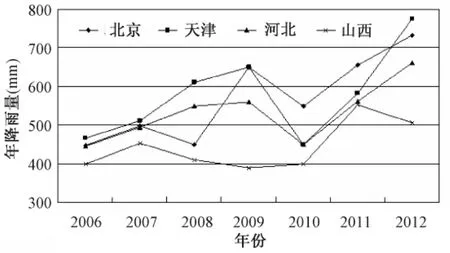
图5 2006~2012年不同区域年降雨量
华北平原地处我国北方半干旱地区,随着经济建设的不断发展,深层承压水被大量超采,引发了地下水位降落漏斗、地面沉降和咸水界面下移、地面塌陷等一系列地质环境问题(杨丽芝等,2013)。杨明波等(2009)曾对北京地区地下水位动态特征的成因作了详细分析,认为影响地下水位的主要因素是地下水开采和降雨,地下水位的趋势性变化则与区域地下水超量开采有直接关系,而具有明显长期下降趋势的北京昌平井正是处于严重超采的区域。因此,进一步搜集了华北地区不同区域的年度地下水单位面积蓄变量①,其中北京、河北、山西等地的累计年蓄变量呈明显的趋势性下降(图6),与该区域内水位井的趋势性下降形态相一致;天津地区的沉降漏斗区基本覆盖南部平原区,整个区域地下水均处于超采状态(董克刚,2010);而鲁豫交界地区深井水位的下降主要受周边地热开采的影响(孙小龙等,2013)。
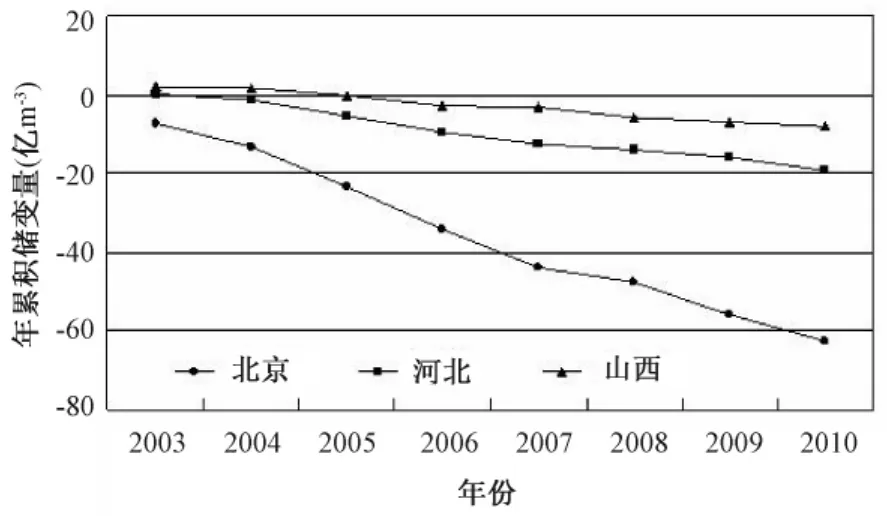
图6 2003~2010年北京、河北、山西地下水单位面积年累计蓄变量
通过上述分析可以判断,华北地区多年接近线性下降的井水位绝大部分都是由于外界干扰导致的,并不是区域应力应变的反映。由于具有这种变化的井孔数量较多,变化幅度也较大,因此有必要对这些数据进行处理,否则会影响我们对含水层应力应变情况的分析,故本文采用K-L法最佳直线拟合去除了这16口井水位的线性变化趋势(图7)。
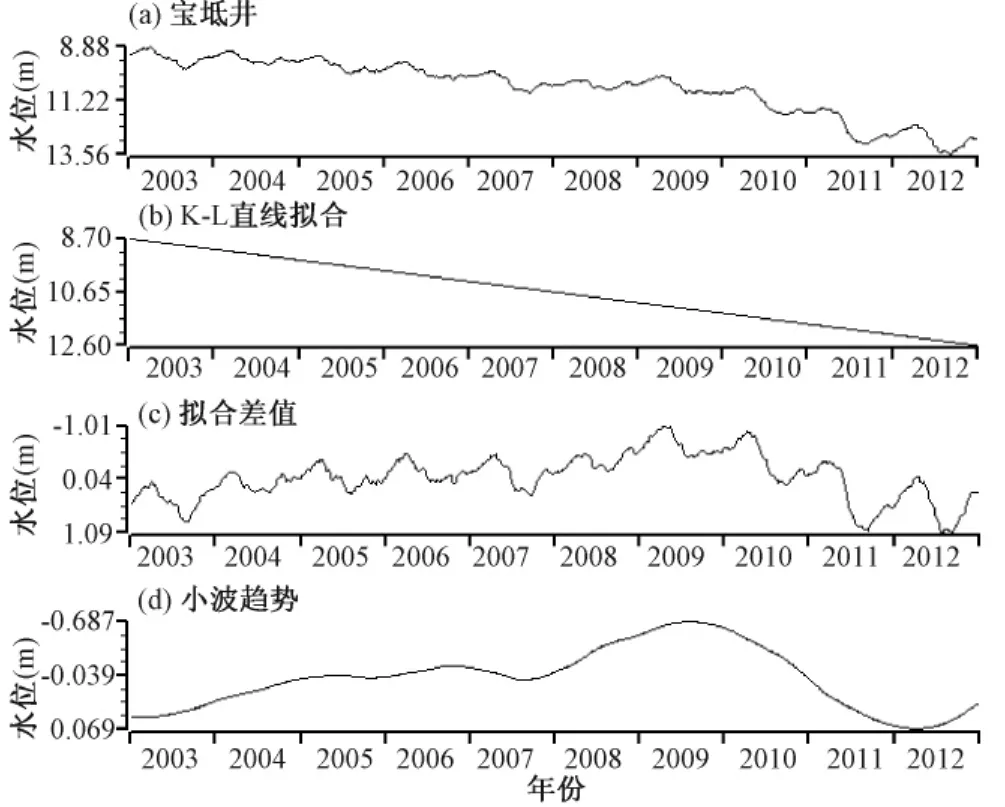
图7 宝坻井水位及处理后的趋势性变化
上述处理过后,由于水位数据中除了含有长趋势的变化,还包含着年变动态、月变和日变以及其他频率的干扰波动。因此若要提取较长时间内比如年度或半年尺度上的水位变化,还需要从水位的原始曲线中提取出长趋势变化动态。本文采用小波趋势分析方法提取33口井水位的趋势变化,根据前人研究成果(万永芳等,2009)并通过计算对比,选取了db4小波基的5阶或6阶分解结果(图7(d))。
5 反演华北地区井含水层体应变
反演华北地区井孔含水层体应变,首先利用第4节中小波方法提取的井水位趋势变化数据,计算出各井每半年的水位平均值,将前后两个水位半年平均值逐步相减,得到每半年各井水位的变化值dh;然后将已经计算好的各井潮汐因子值与水位变化量代入式(1)进行计算,求得各井所反映的含水层体应变量ΔΘ,最后运用径向基插值法,得到华北地区半年尺度的应力应变场的变化图像(图8)。
图8是反演得到的华北地区2009~2012年应力应变场变化图像。由图8可见,变化比较明显的区域主要集中在山西中南部和首都圈地区。首都圈地区在2009年下半年和2012年都出现了应力应变集中的情况,这种集中主要表现为一种应力应变增强与减弱相交的四象限分布特征,与区域应力场背景相符。2010年首都圈地区发生了2次4级地震,分别是3月6日河北滦县MS4.2地震和4月9日河北丰南MS4.1地震,由图8可以看到,2009年下半年首都圈地区出现了一定程度的应变集中,到2010年上半年该集中有所减弱,这与2次地震的发震时间相符。2012年的2幅图在首都圈地区都清晰地出现了应变集中,幅度比2009年的更大,而2012年首都圈地区相继发生了5月28日河北唐山MS4.8地震、6月18日天津宝坻MS4.0地震和8月26日天津宝坻MS3.5地震。其中最为显著的唐山MS4.8地震的震源机制解为右旋走滑类型(张跃刚等,2013),该结果与图8中显示的首都圈地区计算的体应变拉张压缩分布形态比较相似。
图8显示,山西中南部地区2009和2010年呈现一种压性减弱(拉性增强)的状态,2012年下半年变为压性增强(拉性减弱)状态。2009~2010年山西地区发生的最大地震是1月24日山西河津MS4.8地震,该地震的震源机制解类型是以正断为主兼走滑(宋美琴等,2012),而2009~2010年其他几次中等地震也均是以正断或走滑为主的地震活动。2011年以后,山西地区地震活动较为平静,没有显著的地震事件发生。
6 结论与讨论
本文选取华北地区33口水位井的整点值数据,经过去除气压效应、长周期趋势和滤波处理提取了水位固体潮信息,计算出井孔水位的潮汐因子,并采用积分格林函数方法剔除了距海岸线较近水位井的潮汐因子的海潮负荷;同时,通过对水位趋势性变化的分析,粗略地去除了部分受外界影响较大的水位井的线性趋势;最后以半年为时间尺度对选取的华北地区井水位进行了反演计算,得到了以半年为尺度的应力应变场的动态变化图像。
由计算结果可见,井孔分布较为密集的首都圈地区,在显著地震前呈现出一种拉张、压缩相交的近似四象限分布的状态;而对于井孔分布较少的山西带则基本呈现出单纯的拉张或压缩的应力集中状态,这种情况与当时的区域应力状态有一定关系,但也与本文选取的井孔分布不均匀有关。张昭栋等(2001)曾利用井水位资料反演了大同-阳高6.1级地震前后大区域应力场的动态变化图像(38°~42°N,114°~121°E),在地震前后该区域也呈现一种“正应力”与“负应力”交织的状态,与2012年唐山4.8级地震前后的空间图像较为相似(图8)。曹井泉等(2004)利用应力变化响应系数反演了1976年唐山7.8级地震前后3年京津唐地区的应力场变化情况,在该次地震前震中区和周边地区出现了应力应变集中的有序变化。结合上述震例可以看出,本文对华北地区井水位含水层体应变的反演在一定程度上反映出了该区域深层的应力应变状态。
在本文的研究时段内,华北地区的许多井孔由于受到区域地下水超采等情况的影响而出现了趋势性下降,本文采用K-L直线拟合的方法去除了这一影响。由于这种方法比较简单,并不能完全模拟环境干扰对井水位的影响,因此还需要进步一研究更贴近实际的干扰去除方法。

