某无人机液压起落架系统建模与仿真

卫 晶 ，任 杰，袁冬莉

（1.西北工业大学 自动化学院，陕西 西安 710029；2.中航工业成都飞机工业（集团）有限责任公司 四川 成都 610031）

某无人机液压起落架系统建模与仿真

卫 晶1，任 杰2，袁冬莉1

（1.西北工业大学 自动化学院，陕西 西安 710029；2.中航工业成都飞机工业（集团）有限责任公司 四川 成都 610031）

某无人机液压系统主要为起落架的收放提供动力源，对其进行建模仿真能够实现参数和方案的优化，以便获得最佳的设计。基于节点法的集中参数数学建模思想，针对液压系统的动态特性仿真问题，研究了在MATLAB/SIMULINK下面向液压元件的液压系统动态特性仿真模型库的建立问题，建立各液压子系统模型，进行无人机液压起落架仿真，得到起落架收放时间短，达到某无人机起落架对响应时间的要求。

无人机；液压系统；起落架；节点法

某无人机液压系统作为起落架的收放动力源，其响应速度和响应时间对于起落架的安全收放具有重要意义[1]。计算机数字仿真可以帮助液压系统设计人员在设计阶段就较准确地预测出设计对象具有的静态、动态特性，能够实现参数和方案的优化，以便获得最佳的设计[2]。利用SIMULINK工具箱可方便地通过多种建模途径对液压元件和系统进行建模，最大程度地突破了专用软件在建模方法和模型库方面的限制；很多研究人员希望仿真模型对自己是完全透明的，恰好SIMULINK也提供了这样的条件针对液压系统的动态特性仿真问题。

基于节点法的集中参数数学建模思想，研究了在SIMULINK下面向液压元件的液压系统动态特性仿真模型库的建立问题，建立各液压子系统模型，进行无人机液压起落架仿真。

1 液压系统建模

液压传动的理论依据主要是流体力学中的帕斯卡原理、连续性原理和能量守恒定律。力的传递靠静压传递方程，即帕斯卡原理来实现；速度的传递靠流体连续性原理实现，能量的转换和传递遵守能量守恒定律。

液压系统可以看成由多个元件构成，各元件间能量的传递经过液压管道来实现。如果忽略管道效应或按集中参数模型来考虑管道效应，多个元件之间的管道可以看成液压容腔。数字仿真中，可以采用节点法建立液压系统的集中参数数学模型，把液压管路的汇交点定义为节点，对每个节点建立流量平衡方程表达节点压力和进出该节点流量之和的关系。对于一个液压容腔节点，基于基尔霍夫节点法描述该节点上的流量平衡：

式中，Vi是容腔vi的体积。ΣQi为进出容腔Vi的流量之和。

此压力方程中的流量关系就对应于液压回路中的构件连接关系。根据这一原则，可以建立任何液压回路的数学模型。如图l所示的液压起落架系统回路。图2所示为容腔节点图。

1）在起落架挡板没有到位时，开关B5是关闭的，此时系统包含有Vl和V2两个容腔，当收放电磁阀打到“放下”端，放下起落架时，红色线路为进油线路，蓝色为回油线路。是油泵B1的输出流量，QB21、QB31、QB41分别是进入左档板、右档板、前档板液压油缸B2、B3、B4无杆腔的流量，QB22、

QB33、QB43分别是从左档板、右档板、前档板液压油缸B2、B3、B4有杆腔流出的流量，QB10是通过液压油滤B10的流量。

此时，它们的压力建立方程如下：

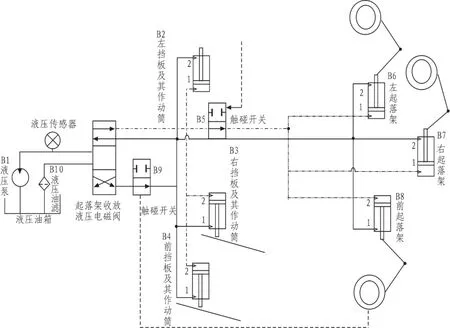
图1 液压起落架系统简易回路Fig.1 Simple loop of hydraulic landing gear system

2）在起落架挡板到位时，开关B5被触碰打开，挡板作动筒被锁住，不参与系统流量压力变化，开关打开后，油液流向起落架作动筒，此时系统包含有V3和V4两个容腔，红色线路为进油线路，蓝色为回油线路。此时，它们的压力建立方程如下：

式中，QB61、QB71、QB81分别是进入左起落架、右起落架、前起落架液压油缸B6、B7、B8无杆腔的流量，QB62、QB72、QB82分别是从左起落架、右起落架、前起落架液压油缸B6、B7、B8有杆腔流出的流量。

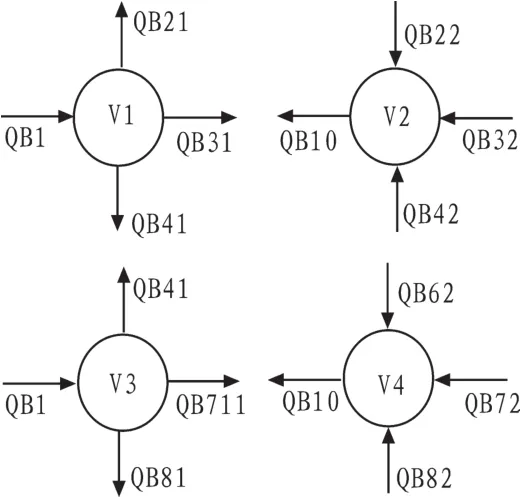
图2 容腔节点图Fig.2 Vessel node

这样液压系统就可以由一阶微分方程组来描述各容腔压力的动态变化特性。对于各构件，建立各自的流量——压力方程，与压力建立方程联立求解，就可以对液压系统各容腔的压力值进行动态特性仿真。

2 液压回路仿真模型库的建立

基于面向对象的仿真建模思想，可以将液压回路视为由各个液压元件构成，各液压元件之问通过油口相连接。这些液压元件包括液压容腔、液压油泵、各类液压阀及液压油缸等。在对系统一个具体的液压系统仿真时，可以直接从已建立的Simulink模型库出获得功能模块，按能量传递关系进行连接后，就可以进行仿真，可以提高仿真效率。

2.1 液压容腔

描述液压容腔的基本方程为式（1），其输入为流入或流出该容腔的流量代数和，输出为容腔的压力，如图3中“Vi”模块所示。考虑到模型库的通用性，在容腔仿真模块的建立中，还要考虑容腔容积在系统运行过程中可能发生变化。当容腔与液压油缸相连接时，由于活塞杆的运动，相应容腔的体积要发生变化。

因此，模块Vi的输入Q包括两项内容：与该容腔相连的液压元件输入或输出的流量之和，及各液压元件的运动对该容腔容积产生的变化量。

V0为容腔的初始容积，ΔV为容腔容积的变化量，P0为初始压力。积分器可给定初始值16 MPa。

2.2 液压泵

利用半经验模型，在液压泵流量恒定的前提下，驱动功率和液压泵的工作压力成正比例关系。一般液压泵配有安全活塞，在压力超过设定压力时会有回油。所以，液压泵的输出流量Qp的表达式为等式（5）。对于液压油泵，以转速和油泵出口压力为输入，以油泵出口流量为输出，建立油泵的流量输出方程：设定Pset为18 MPa。

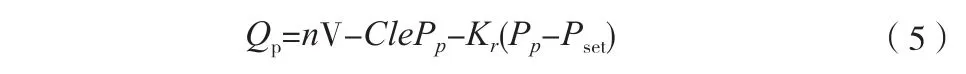
2.3 液压缸

液压缸是液压系统的执行元件，用来实现直线往复运动或回转摆动。杆运动位移 、速度 为输出，建立描述液压油缸运动的一阶微分方程组：

图4 液压缸Fig.4 Hydraulic cylinder

在对上式进行仿真建模时，考虑活塞杆的运动队容腔容积产生影响

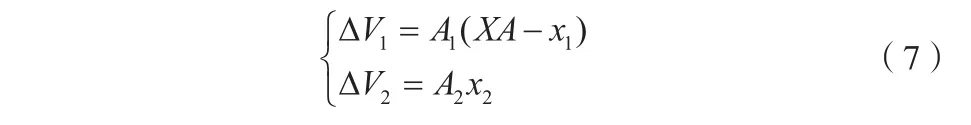
还要考虑活塞杆运动到极限位置时的限位问题。采用接触变形模型，设油缸壳体和活塞杆的材料变形刚度K很大，将碰撞限位用一个弹簧力来等效，得到碰撞力F1的表达式：

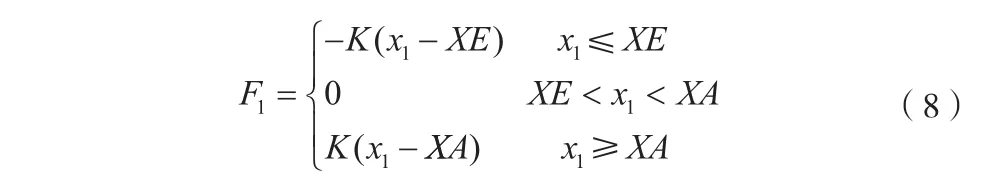
式中，XE，XA分别为活塞杆位移的下限位、上限位。在Simulink下建立碰撞力模型，作为一个子模块，其中用XW表示位移量x1，如图5液压缸模型。

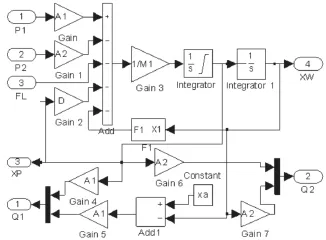
图5 液压缸建模Fig.5 Model of hydraulic cylinder

2.4 阀和管道

图l所示的液压回路，液压系统作为收放起落架的动力源，其阀和管道的数量较多，实际系统远比图1画出的系统要复杂，这里将其等效成一个阀和管道的损失来计算，可简化建模。液体在等径直管中流动时因粘性摩擦而产生的压力损失称为沿程压力损失。

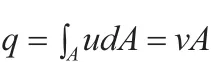
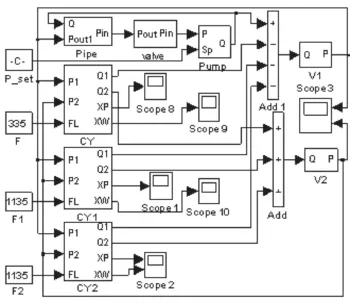
图6 液压仿真系统Fig.6 Simulation of hydraulic system

于是积分可得：

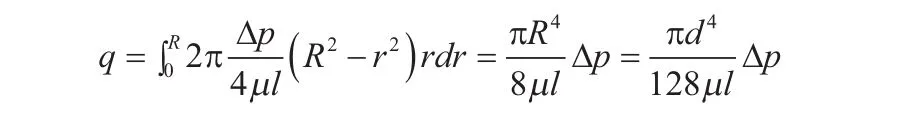
取管道有压力损失无流量损失，沿程压力损失为：

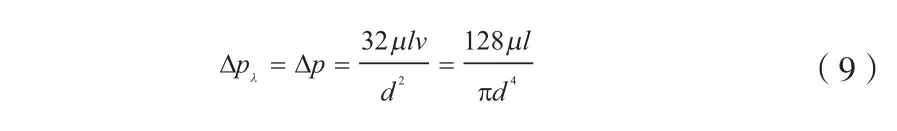
表1 文中用到的变量及给定值Tab.1 The variables and the given value in this paper

3 液压仿真系统

根据上述各个液压元件的建模原理和模型构造，能够得到每个部件的压力、流量的传递关系。将所有部件按照物理流程进行连接可得到如图6的液压仿真系统。取前起落架的负重为335 ，主起落架的负重为1135 。

由于液压系统起落架收放前要对挡板进行收放，两个过程近似，在时间上看，起落架作动和挡板作动的时间可以近似一致。下面仅对液压源驱动起落架液压缸部分进行仿真。

根据图7和图8可以看出液压缸活塞的速度和位移关系。活塞的速度为0后，活塞不再移动，处于满足系统给定压力的情况下。两者到达稳定状态的时间在0.2 s以内。时间较短，挡板作动的过程近似，估计时间也在0.2 s左右。

图7 前起落架液压缸图Fig.7 Front landing gear

图8 主起落架液压缸Fig.8 Main landing gear hydraulic cylinder

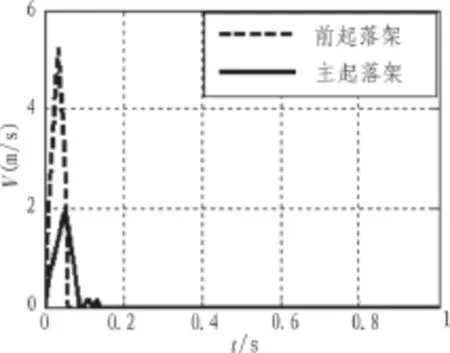
图9 前后起落架的位移对比Fig.9 Comparison of landing gear displacement

比较图9和图10可知，前起落架的运动速度比较快，位移较大，因为飞机一般仰头，前起落架的作动较长，符合实际情况，根据响应时间可以判断出建模及仿真是有效的，能够满足在短时间内收放起落架的要求。

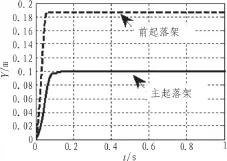
图10 前后起落架的速度对比Fig.10 Comparison of landing gear speed

4 结 论

根据液压系统特性，采用节点法，对系统整体流程进行建模。根据液压系统各个部件的物理特性，得到流量和压力的传递形式，进行模型库的建模。组合模型库各个部件，得到某无人机的液压起落架系统利用simulink过对系统进行仿真，得到作动筒的响应曲线和响应时间。综合整个系统考虑，时间上完全符合30 s内收放起落架的要求。证明此系统的可行性和实现性。

[1] 高钦和，龙勇，马长林，等.机电液一体化系统建模与仿真技术[M].北京：电子工业出版社，2012.

[2] 张立军，赵升吨，刘克铭.中高压液压缸实验台液压系统仿真及优化[J].系统仿真学报，2007（2）：67l-674.

ZHANG Li-jun，ZHAO Sheng-dun，LIU Ke-ming.Simulation and Parameter Optimization of Test Platform Hydraulic System Based on Mesohigh Cylinder[J].Journal of System Simulation，2007（2）：67l-674.

[3] 田树军，张宏.液压管路动态特性的simulink仿真研究[J].系统仿真学报，2006（5）：1136-1138.

TIAN Shu-jun，ZHANG Hong.Study on Simulation of Hydraulic Pipelines' Dynamic Characteristic By Simulink Software[J].Journal of System Simulation.2006（5）：1136-1138.

[4] 宋志安，曹连民，黄靖，等.MATALB/Simulink与液压控制系统仿真[M].2版.北京：国防工业出版社，2012.

[5] 李永堂.液压系统建模与仿真[M].北京：冶金工业出版社，2003.

[6] 李异河，丁问司，孙海平.液压与气动技术[M].北京：国防工业出版社，2006.

[7] 高钦和，郭晓松，液压回路计算机仿真中阀口流量模型的改进[J].计算机工程与应用，2003，29（12）：209-21l.

GAO Qin-he，GUO Xiao-song.A Modified Orifice Flow Model for Hydraulic Circuit Simulation[J].Computer Engineering and Applications.2003，29（12）：209-21l.

[8] 薛定宇，陈阳泉.基于MATLAB，SIMULINK的系统仿真技术与应用[M].北京：清华大学出版社，2002.

Modeling and simulating of a UAV hydraulic system

WEI jing1，REN jie2，YUAN Dong-li1
（1. College of Automation，Northwestern Polytechnical University，Xi'an 710129，China；2.AVIC Chengdu Aircraft Industrial（Group）CO.，Ltd，Chengdu 610031，China）

A certain unmanned aerial vehicle hydraulic system mainly provides power to the landing gear system.Modeling and simulating the hydraulic system is good for optimization parameters and algorithm to obtain the better design.Aimed at the simulation characters of hydraulic system，the structure and function of hydraulic system are analyzed，and based on points focus calculation，the mathematic models of components for hydraulic pump，brake valve，brake cylinder and so on are established to the hydraulic system.Simulation experiment based on Matlab/Simulink proves that the duration of system meets the requirement of the UAV.

Unmanned Aerial Vehicle（UAV）；hydraulic system；landing gear；points focus calculation

V227+.4

A

1674-6236（2014）11-0008-04

2013-09-10 稿件编号：201309078

国家自然科学基金（60974146）

卫 晶（1988—），女，黑龙江齐齐哈尔人，硕士研究生。研究方向：控制理论与控制工程。