EMD-ICA与SVM在滚动轴承故障诊断中的应用
杨伟新,王 平
(中国航空动力机械研究所 航空发动机振动技术航空科技重点实验室,湖南 株洲412002)
EMD-ICA与SVM在滚动轴承故障诊断中的应用
杨伟新,王 平
(中国航空动力机械研究所 航空发动机振动技术航空科技重点实验室,湖南 株洲412002)
针对滚动轴承非线性的早期故障信号,应用独立分量(ICA)将滚动轴承产生的故障信号从多通道混合信号中分离出来,然后采用EMD(Empirical Mode Decomposition)进行再次降噪并建立AR模型,最后提取模型的自回归参数和残差方差作为故障特征向量,并以此作为支持向量机(SVM)分类器的输入参数来区分滚动轴承的工作状态和故障类型。实验结果表明,该方法是有效的。
振动与波;滚动轴承;独立分量;经验模式分解;AR模型;支持向量机
本文采用基于负熵的快速独立分量(Fast ICA)算法对混叠信号进行独立源信号分离,有效消除各个传感器采集信号的数据冗余[5]。然后对二次信号进行EMD分解达到再次降噪,并建立AR模型,以模型参数作为故障特征向量输入SVM建立的分类器,从而判断滚动轴承故障类型。实验表明,EMD-ICA方法和SVM方法相结合能有效地应用于滚动轴承的故障诊断中。
1 EMD-ICA方法
EMD分解就是将信号分解成多个能表征模糊频带和瞬时频率双重信息的IMF分量,其中每一个IMF必须满足以下两个条件:1)整个信号序列中,极值点数与过零点数必须相等,或最多相差一个;2)在任一时间点上,信号局部极大值、极小值所确定的上、下包络线均值为零。
由文献[6]知,原始信号x(t)的EMD分解可表示成
式中rn(t)表示趋势分量,而各个IMF分量ci(t)(i=1,2,...,n)分别包含了信号从高到低不同频率段的成分。
Fast ICA算法又称固定点算法[7],是由荷兰赫尔辛基大学Hyvariner等人提出来的。该算法采用牛顿迭代算法对观测变量x的大量采样点进行处理,以最大负熵作为目标函数,每次从观测信号中分离出一个独立成分,是独立分量分析的一种快速算法。下面归纳Fast ICA算法流程:(1)对混合信号去均值,并球化预处理,得z;(2)任意选择具有单位方差的初始分离矩阵ωi(0),要求‖ωi(0)‖2=1;
(3)选择一个初始权失量(随机的)ui(k),令其中E(·)为均值运算,分别为所选的非线性函数及其导数,可取f(·)=tanh(a1·),这里,1≤a1≤2,通常我们取a1=1;
(5)如未收敛,回到步骤(3)。
基于Fast ICA算法的优点有两个方面,一是由于采用牛顿法,收敛较有保证;二是迭代过程中无需引入调节步长等人为设置的参数,因而更简单方便。
2 SVM原理

图1 最优分类线
SVM是从线性可分情况下的最优分类面发展而来的,基本思想可用图1的两维情况来说明。图中,五角星和圆圈分别代表两类样本,H为分类线。H1,H2分别为过各类中离分类线最近的样本且平行于分类线的直线,它们之间的距离叫做分类间隔(Margin),其中分类线H1和H2上的训练样本点就称作支持向量。所谓最优分类线就是要求分类线不但能将两类正确分开(训练错误率为0),而且使分类间隔最大。分类线方程为x·ω+b=0,对它进行归一化,使得对线性可分的样本集(xi,yi),i=1,…,x∈Rd,y∈{+1,-1},满足
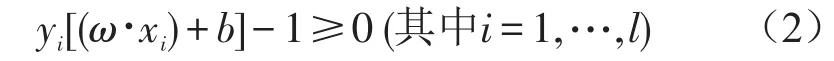
此时分类间隔等于2/‖ω‖,使间隔最大等价于使‖ω‖2最小。满足条件(2)且使(1/2)‖ω‖2最小的分类面就叫做最优分类面,目标函数是严格上凹的二次型,约束函数是下凹的,这是一个严格凸规划。按照最优化理论中凸二次规划的解法,我们把它转化为Wolfe对偶问题来求解[8]

其中 αi正是样本点xi的Lagrange乘子。Kuhn-Tunker条件定理指出[9],无效约束所对应的Lagrange乘子一定为0,在这里的物理意义也就是说非支持向量xi的Lagrange乘子一定为0。这样分类规则就仅由恰好在最优分类面边缘上的少数支持向量(对应着约束yi[(ω·xi)+b]-1=0)来决定,而与其它样本无关。
3 EMD-ICA与SVM的故障诊断方法
EMD-ICA与SVM结合的滚动轴承故障诊断方法如下:首先通过Fast ICA从传感器测取的混合信号中提取出滚动轴承系统运行产生的故障信号,然后对其进行EMD分解,得到多个IMF分量,重构并建立AR模型,提取模型的自回归参数和残差方差作为故障特征向量输入SVM建立的分类器,最后判断滚动轴承故障类型,其分析流程如图2所示。

图2 分析流程图
4 实例应用
本文采用型号为6203-2RS JEM SKF的深沟球滚动轴承,其相关参数为滚珠数z=9,转速n=1 796 r/min,采样频率为12 kHz三通道采样,分别在风扇端、基座处和驱动端安装加速度传感器,分别采集4类状态下(正常、外圈、内圈与滚动体故障)的滚动轴承振动信号各20组数据,其中某一组中外圈故障状态(限于篇幅只列出外圈故障状态)振动加速度信号时域波形如图3所示。

图3 滚动轴承外圈故障三通道信号波形图
由于轴承、其他机械部件以及环境是相互独立的物理系统,因此可以通过Fast ICA运算分析将轴承外圈故障信号从混合信号中分离出来,分离出的波形如图4所示。由图可看出,经Fast ICA运算后的波形冲击成分更加明显了。
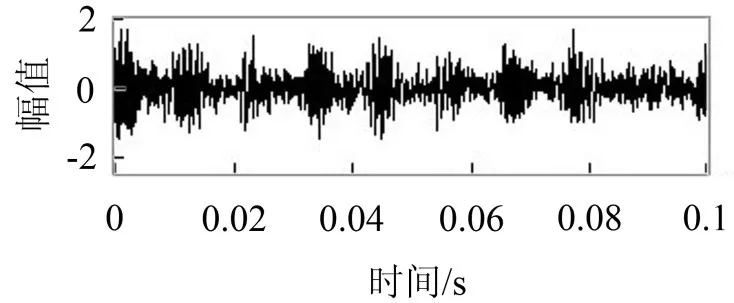
图4 滚动轴承外圈故障信号波形图
由于滚动轴承故障的低频信号通过共振会调制到高频区,从而在高频区表现出极高的能量,故对故障信号进行EMD分解,考虑到EMD分解各分量信号的特性[10,11],所以本例中只取前三个IMF分量。其中IMF1反应了信号的最高频成分,IMF2、IMF3分量的频率依次降低波形如图5所示。

图5 EMD分解及重构波形图
将分量IMF1、IMF2、IMF3进行了重构并建立AR模型,AR模型采用快速算法,能满足及时性的要求,AR模型参数和阶数是其建模的主要问题。本文采用文献[12]中最小二乘法和BIC准则,计算模型参数和阶数,此算法计算简单、准确,易于满足实时性的要求,在机械设备工作状态监测中较为实用。最小二乘参数估计的解析表达式为

其中xt是用来建模的平稳时间序列,Rk是自协方差估计。BIC准则的计算公式为
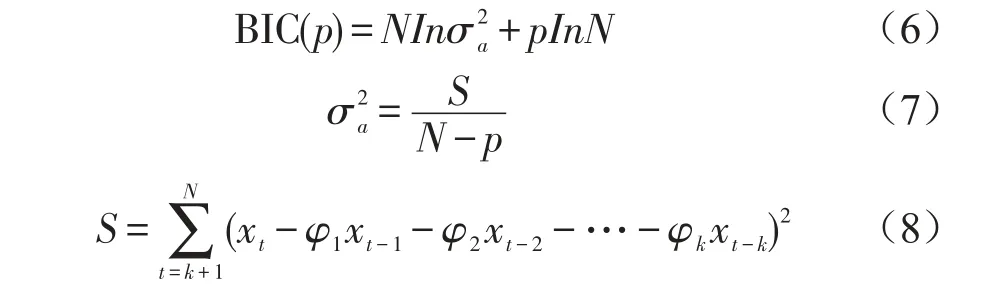
提取前10阶的自回归系数及残差的方差作为SVM分类器的输入参数。4种状态下AR模型自回归参数及残差方差如表1所示。

表1 IMF能量熵值及AR模型参数
设计4个SVM分类器来识别滚动轴承正常状态、外圈故障、内圈故障和滚动体4种类型,4个SVM分类器分别如下:
SVM1:y=+1表示正常状态,y=-1表示故障状态。
SVM2:y=+1表示外圈故障,y=-1表示其它故障。
SVM3:y=+1表示内圈故障,y=-1表示其它故障。
SVM4:y=+1表示滚动本故障,y=-1表示其它故障。
从4种类型数据中各抽取3组作为训练样本,剩余8组(正常状态、外圈故障、内圈故障、滚动体故障各2组)作为测试样本。表2为SVM测试分类结果。由表2看出,SVM对测试样本故障诊断的结果与实际完全相符,说明了该方法的有效性。
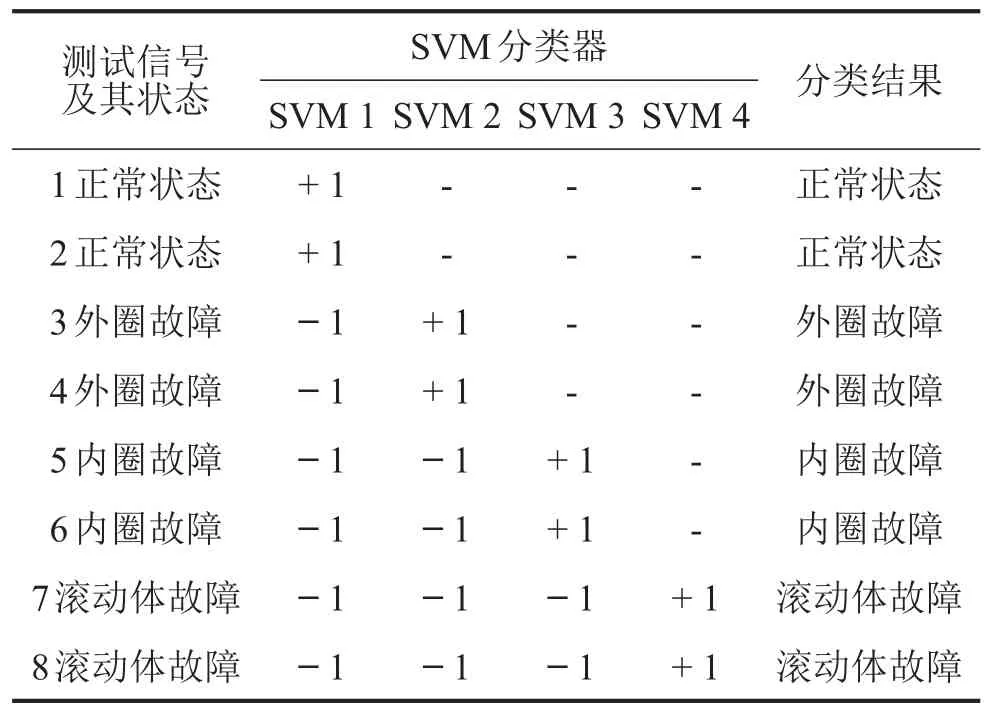
表2 SVM测试分类结果
5 结语
针对从多通道混合信号中分离出滚动轴承故障信号这一问题,采用了ICA分析给与解决;将故障信号EMD分解成多个IMF,并将其进行重构,提高了信噪比且解决信号非平稳性问题,然后与AR模型相结合,提取的模型参数能够正确地反映不同故障类型的特征信息,作为SVM的输入参数,解决小样本问题并能对故障类型进行准确的判别。对滚动轴承正常状态、外圈故障、内圈故障及滚动体故障振动信号分析结果表明EMD-ICA与SVM的结合的有效性。
[1]姚 良,李艾华,王 涛.运用改进二叉树SVM算法的柴油机振动诊断[J].振动、测试与诊断,2010,30(6):689-693.
[2]焦卫东,杨世锡,吴昭同.机械故障模式识别的ICA基神经网络方法[J].农业机械学报,2004,35(4):151-154.
[3]邓卫强,王跃钢,杨颖涛,郑文达.一种改进的ARMA模型参数估计方法[J].振动、测试与诊断,2011,31(3):378-380.
[4]Huang N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond A,1988,454:903-995.
[5]钟振茂,陈 进,钟 平.盲源分离技术用于机械故障诊断的研究初探[J].机械科学与技术,2002,21(2):282-284.
[6]Rai V K,Mohanty A R.Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform[J].Mechanical Systems and Signal Processing,2008,22:905-914.
[7]杨福生,洪波著.独立分量分析原理与应用[M].北京:清华大学出版社,2006.
[8]Nello Cristianini,John Shawe-Taylor.支持向量机导论[M].北京:电子工业出版社,2004,3.
[9]范劲松,陶 卿,方廷健.统计学习理论优化感知器的遗传算法.模式识别与人工智能[J].2001,14(2):211-215.
[10]王 珍,郭 方,江亲瑜.EMD的Lab VIEW实现及其在滚动轴承故障诊断中的应用[J].噪声与振动控制,2009,8(4):54-57.
[11]杨伟新,江亲瑜,王 珍,郭 方.EMD与高阶累积量在滚动轴承故障诊断中的应用研究[J].噪声与振动控制,2011,3(5):142-145.
[12]杨叔子,吴 雅,轩建平,等.时间序列分析的工程应用[M].武汉:华中科技大学出版社,2007,6.
Application of EMD-ICAand SVM in Fault Diagnosis of Rolling Bearings
YANG Wei-xin,WANGPing
(Key Laboratory ofAero-Engine Vibration Technology inAeronautical Science, Zhuzhou 412002,Hunan China)
Aiming at the early non-linear fault signals of rolling bearings,the ICA is employed to separate the fault signals of the rolling bearing from the mixed signals collected by the multi-channel.Then,the EMD method is used to reduce the noise and establish the AR model.Finally,the self-regressive parameters and the residual square difference of the model are extracted and regarded as the fault characteristic vectors.They are used as the input parameters of the SVM classifier to distinguish the working condition and the type of faults of the rolling bearing.Experimental results show that this approach is effective.
vibration and wave;rolling bearing;ICA;EMD;AR model;SVM
1006-1355(2014)03-0182-04
TH133.4;TP206+.3
A
10.3969/j.issn.1006-1335.2014.03.038
在滚动轴承故障诊断中,基于人工神经网络的模式识别方法以其较强的自组织、自学习能力和非线性模式分类性能得到了广泛应用。但人工神经网络需要大量的典型故障数据样本或经验知识,而在实际生产当中,一般来讲很难获得大量典型的滚动轴承故障样本。SVM是一种利用小样本去解决数据分类问题的有效工具[1],其可以采用少量的时域故障数据样本训练故障分类器,便可实现多故障的识别和诊断。然而,滚动轴承早期故障信号往往被旋转机械其它部件和环境激发的噪声信号所污染,这使得所测信号只能是多个振源的混合,其将导致故障诊断的难度加大且准确性降低。因此,有必要在采用SVM对滚动轴承故障分类之前对原始信号进行预处理来提取故障特征,以获得更好的分类效果。事实上,在机械源分离方面ICA方法已得到了广泛应用[2],另外AR模型的特征向量浓缩了原时间序列信号的全部信息,因此采用AR模型的特征向量参数作为特征向量来分析系统的状态是十分有效的[3]。但AR模型只适用于平稳信号的处理。EMD又称经验模式分解[4],是一种适于非线性、非平稳信号分析的新方法,是一种自适应的信号分解方法,能把复杂的信号分解成有限个IMF分量。进而弱化了信号的非平稳性,使之更适合建立AR模型。
2014-08-08
中航工业技术创新基金:(基金编号:2012B60804R)
杨伟新(1988-),男,江西临川人,硕士,目前从事航空发动机振动与噪声相关研究。
E-mail:ywxdlu@sina.com

