应用移动质量法与分形维数实现梁损伤检测
陈小超,毛崎波
(南昌航空大学 飞行器工程学院,南昌330063)
应用移动质量法与分形维数实现梁损伤检测
陈小超,毛崎波
(南昌航空大学 飞行器工程学院,南昌330063)
以简支裂纹梁为例,利用移动质量法结合分形维数方法实现结构损伤检测。由于质量块在振动梁不同位置时对梁固有频率的影响不同,所以当质量块沿着梁长度方向移动时可以得到一组梁-质量块系统的固有频率曲线,通过分析这组固有频率的分形维数曲线确定梁的损伤位置及其损伤程度。随后讨论附加质量块大小和分形方法参数选择对损伤检测精确性的影响。数值计算结果表明,该方法能准确的识别裂纹位置和损伤程度。该方法的主要优点在于不需要结构的模态信息,并可以在随机激励下实现。
振动与波;附加质量块;固有频率;分形维数;损伤检测
近年来,基于振动的损伤检测方法越来越受到众多学者的关注。常见的检测方法大都围绕结构模态或者固有频率而展开[1―4]。如果精确预知损伤前后的结构模态振型,我们可以通过数值方法(如小波分析[5]、模态曲率[3,6]等)实现结构损伤检测。但是模态分析相对复杂,费时费力。
基于固有频率的方法通过测量结构损伤前后固有频率的变化来识别结构的损伤,注意到只要测量结构上很少的几个点即可得到固有频率,因而在结构损伤检测过程中被广泛使用。由于该方法不需要进行模态分析就能直接进行损伤检测,大大简化了基于振动的损伤检测方法[1]。但是,基于固有频率的损伤方法的还存在如下问题有待解决:(1)结构损伤所引起的固有频率变化通常都比较小,容易被环境和其他操作噪声覆盖掉而不被发现,导致识别失真;(2)基于固有频率的变化很难实现损伤程度的识别。
为了解决这些问题,Zhong[5,7]最近提出一种移动附加质量方法来检测裂纹位置。通过测量质量块在振动梁不同位置时的固有频率,可以得到梁-质量块系统的固有频率曲线,通过这些曲线包含了裂纹位置和深度的信息。Zhong随后通过小波分析对这组频率曲线进行分析,判断梁的裂纹位置。
本文在文献[5]的基础上,以简支裂纹梁为例,提出基于分形方法分析通过移动质量法得到的固有频率曲线,实现裂纹位置及损伤程度的检测。
1 模型分析
假设一简支裂纹梁,其长度和厚度分别为L和h,如图1所示。裂纹位于x=lc处,裂纹深度h,假设在裂纹梁上布置一可移动质量块(质量M),如果把带有质量块的裂纹梁分为3段,则每段梁的自由振动方程可表示为
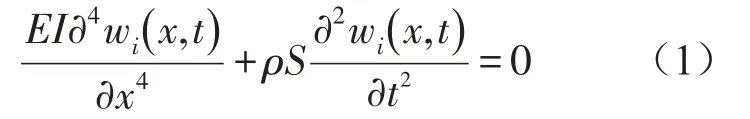
式中p为密度;S为横截面积;E为弹性模量;I为横截面惯性矩;i=1,2,3。
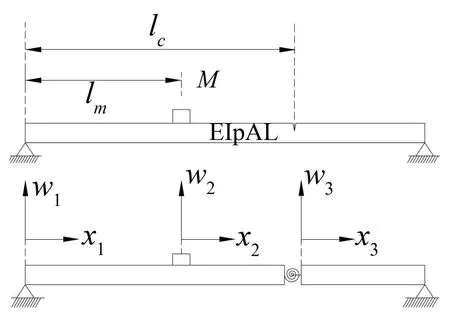
图1 附加质量块裂纹梁模型
根据振动分析理论可知,梁横向位移w(x,t)可以通过分离变量形式表示,即
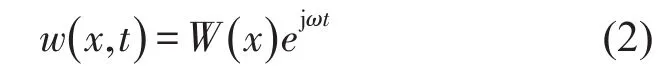
式中,W(x)为结构模态函数,ω为固有频率。
将式(2)代入(1)进行变量分离并将变量无量纲化可得:

第i段梁的结构模态函数Wi可表示为
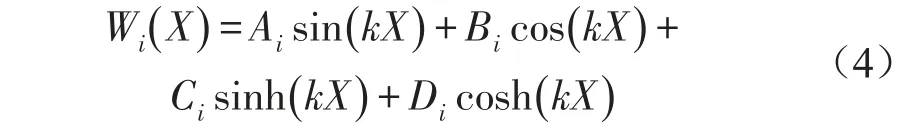
式中Ai,Bi,Ci,Di为待定系数,i=1,2,3。
质量块处连续性条件[8]可表示为
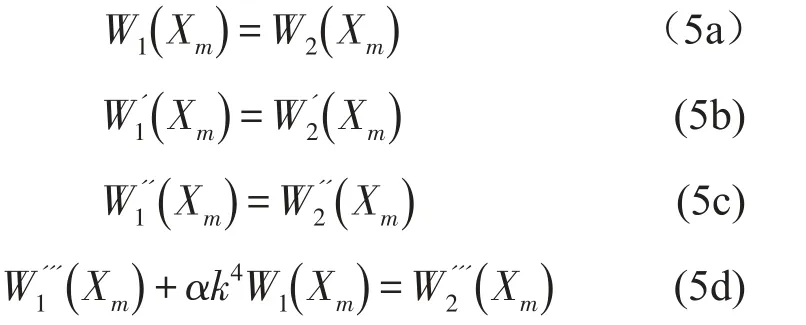
裂纹处连续条件可表示为
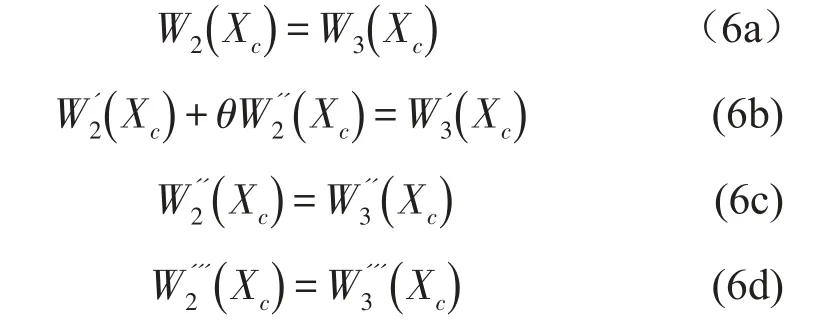
式中θ为裂纹简化成的弹簧的无量纲柔度,θ=5.0346hJ(r),其中r=hc/h,
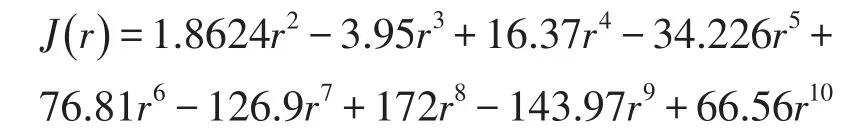
简支梁边界条件表示为
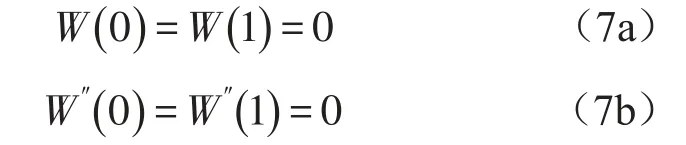
通过式(5—7)即可得到一个12×12的梁的特征矩阵,通过求解该特征方程即可得到含附加质量裂纹梁的固有频率。
2 数值模拟
由于附加质量块的影响,裂纹梁的柔度和惯性矩在质量块附近局部区域会产生变化,这会进一步导致梁固有频率变化。当质量块处于裂纹附近位置时,可以放大裂纹对固有频率的影响。因此,质量块沿着梁移动得到的固有频率曲线包含裂纹的位置和深度信息,在得到固有频率曲线的基础上,我们将基于分形方法检测其裂纹位置和损伤程度。
2.1 损伤识别指标
分形方法最早由Mandelbrot[9]提出,其基本参数分形维数定量描述信号的复杂程度。Esteller[10]比较了波形曲线的Katz、Higuchi、Petrosian算法后发现,对于波形信号曲线,Katz算法有更好的抗噪性。Hadjileontiadis[11]提出了基于Katz算法的梁和板结构响应的检测损伤的分形方法。Hadjileontiadis采用一个定尺度的窗口,计算落入窗口内的曲线片段的分形维数(fractal dimension,FD)。对于梁式结构,滑动窗口沿梁移动则可以得到模态形状的FD曲线。FD值可以用如下公式计算
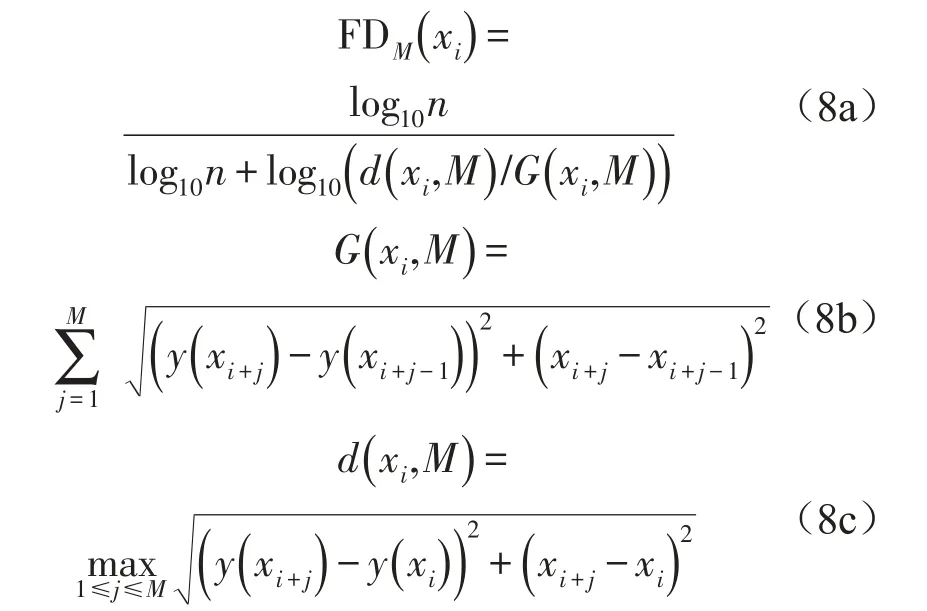
式中n表示离散的曲线总步数;d表示离散序列的第一个点与第i个点之间的直径的最大值;L表示曲线的总长度或者步长的和;M表示窗口尺度。
2.2 损伤识别
选取简支梁为研究对象,假定裂纹位置lc=0.3 L,相对裂纹深度r=5%,质量块与梁的质量比α= 0.1。通过式(5—7)计算得到前4阶无量纲固有频率k随质量块位置变化曲线,如图2所示。
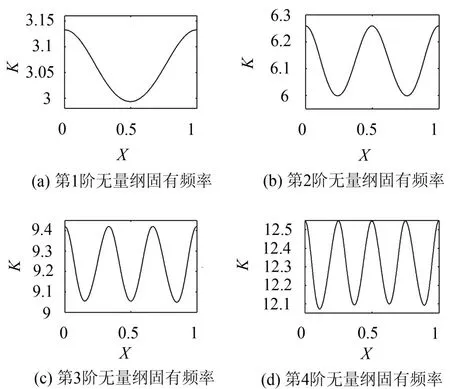
图2 简支裂纹梁—质量块系统前4阶无量纲固有频率(Xc=0.3,r=5%,α=0.1)
从图2可以看出,随着质量块从左端向右移动,固有频率曲线存在波峰和波谷,但不存在直观的不连续点或者其他能直接得出裂纹位置的特征。但是这些曲线包含结构的损伤信息[4],下文将通过FD方法基于这些频率曲线研究损伤监测。
2.2.1 基于FD方法识别损伤位置
首先,通过FD方法识别损伤位置,设定质量块与梁质量比α=0.1,相对裂纹深度r=0.1,并根据裂纹设置的变化设置5种工况,裂纹位置到梁左端距离分别为lc=0.1~0.5L。由于简支梁的对称性,将梁从中点分为两端,仅考虑裂纹处于中点及其左段即可。这5种工况下第1阶无量纲固有频率曲线如图3(a)所示。可以看出,随着裂纹位置由端点处向梁中点移动,固有频率逐渐减小,与Liang得出的结论一致[1]。
通过2.1节所述分形方法计算固有频率曲线的分形维数可得图3(b)。由图3(b)可知,在裂纹所处位置FD曲线均有大的峰值出现。这意味在FD方法可以准确检测出结构的裂纹位置。
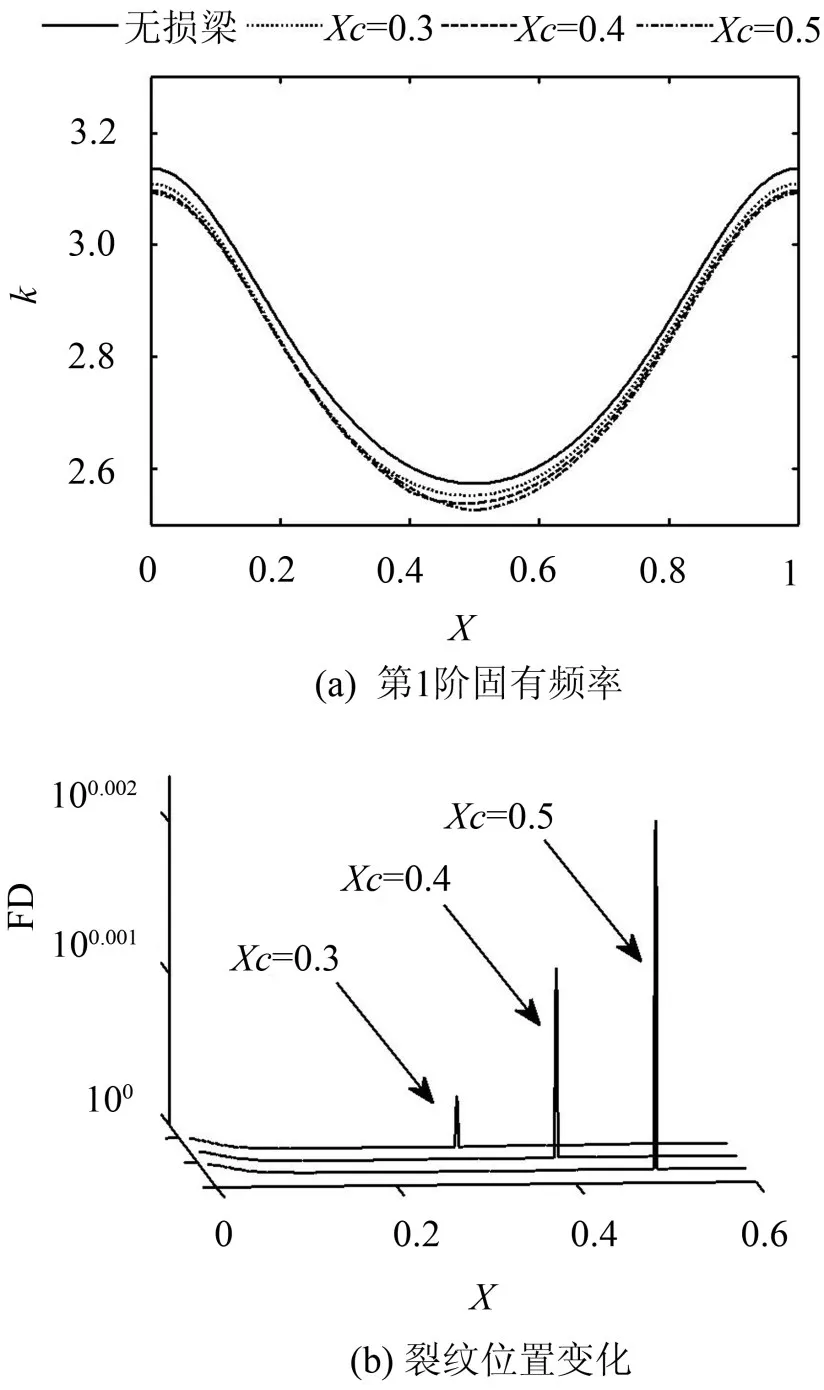
图3 不同裂纹位置时的第1阶固有频率曲线及相应的FD曲线(相对裂纹深度r=0.1)
2.2.2 FD方法对裂纹深度的敏感性
为了进一步通过FD方法识别裂纹的损伤程度,将无量纲质量α设定为0.1,裂纹位置lc=0.3L,假设裂纹深度r从0.1到0.4变化。不同裂纹深度时的第1阶无量纲固有频率曲线如图4(a)所示。从图4(a)可知,随着裂纹深度增加,无量纲固有频率呈减小趋势,且变化率随裂纹深度增加逐渐增大。图4(b)为不同裂纹深度时的的FD曲线。由图4(b)可知,固有频率的FD曲线可以准确地定位裂纹位置,并对损伤程度具有很好的敏感性。图5进一步计算了裂纹位置FD峰值与裂纹深度之间的关系,从图中可以发现,当裂纹深度r为0.05至0.5之间时,FD峰值呈单调增加趋势。这意味着我们可以直接通过FD峰值来判别结构的损伤程度。
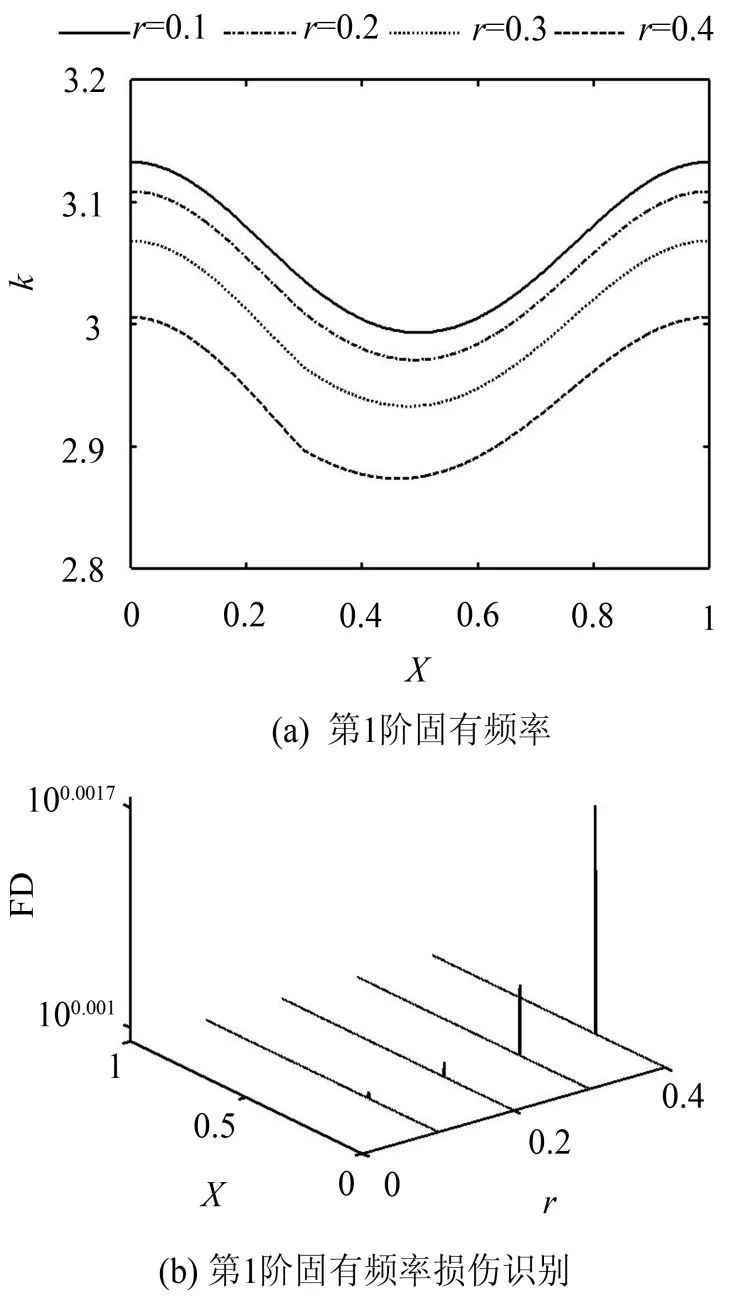
图4 不同裂纹深度时的第1阶固有频率曲线及相应的FD曲线(裂纹位置lc=0.3L)
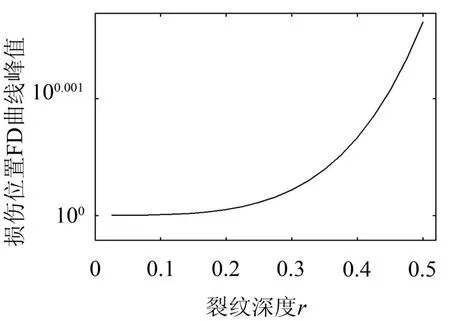
图5 裂纹深度与FD峰值关系
2.2.3 质量块大小对损伤检测的影响
为了进一步研究质量块大小对损伤检测的影响,分别设定质量块与梁的质量比α为0.1,0.2,0.3,0.4。假设裂纹位置位于lc=0.3 L,裂纹深度r=5%。这四种工况下,质量块沿梁移动得到第1阶无量纲固有频率曲线如图5(a)所示。由图5(a)可以发现,第1阶频率随着质量块增大而减小,在波谷位置变化率最大。固有频率FD曲线如图6(b)所示,FD曲线在x/L=0.3处(裂纹位置)出现峰值。图7给出了质量比α从0.1增加到1时FD曲线裂纹处峰值变化曲线;由该曲线可以看出,随着质量比α增大,FD曲线峰值逐渐增大,且变化率逐渐减小。α=0.1~0.5区间FD曲线峰值变化率较大,α=0.5~1区间变化率很小,因此,质量比取0.4~0.6为宜。
2.2.4 双裂纹检测
为了进一步检验本文FD方法对多裂纹损伤梁的有效性,本文设定两条相似裂纹分别处于对称位置和非对称位置两种工况。工况1:第1条裂纹位置lc1=0.3L,相对裂纹深度r1=0.1;第二条裂纹位置lc2= 0.4L,相对裂纹深度r2=0.13。工况2:第1条裂纹位置lc1=0.3L,相对裂纹深度r1=0.1;第二条裂纹位置lc2=0.7L,相对裂纹深度r2=0.13。两种工况的质量比α均为0.1。这2种工况下FD曲线如图8所示。由图8知,在FD曲线在裂纹位置处均出现峰值。其中,图8(b)显示了两条裂纹处于对称位置(工况2)时的FD曲线,第二条裂纹(r2=0.13)处FD峰值大于第一条裂纹(r1=0.1)处FD峰值,证明双重裂纹时FD方法对裂纹深度仍然具有敏感性。
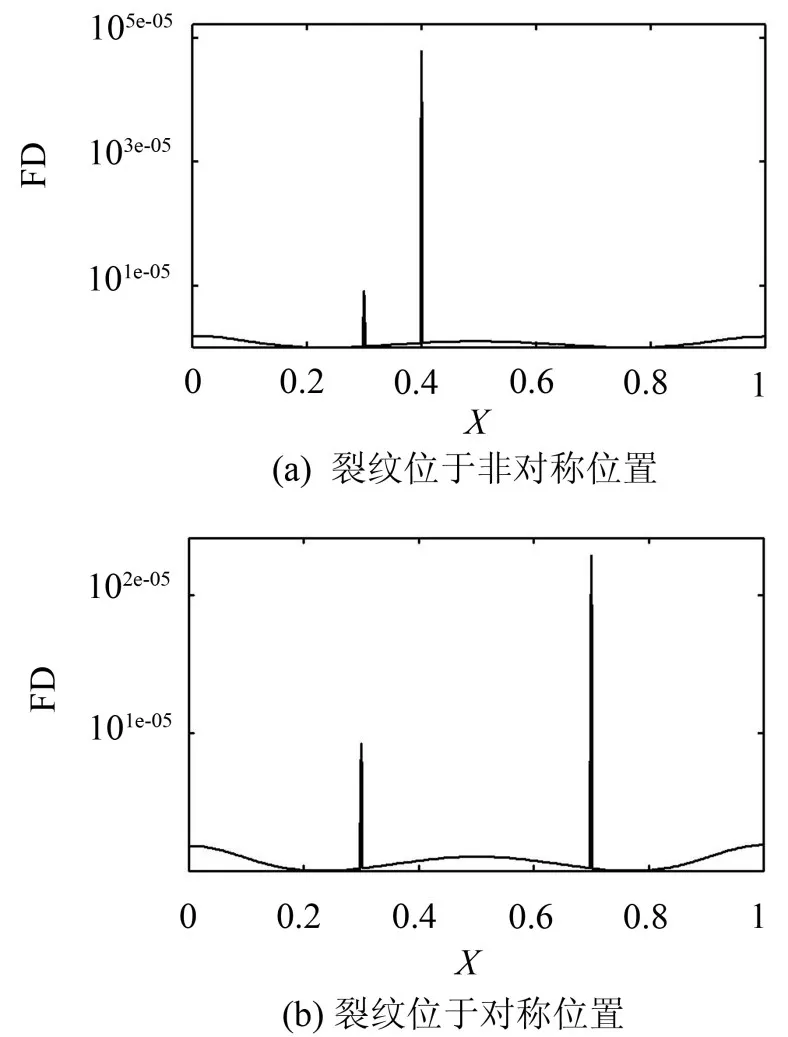
图8 基于分形方法的双裂纹检测
3 结语
本文以简支裂纹梁为例,提出通过移动质量法结合分形方法实现其损伤检测,首先基于振动理论得到质量块位于不同位置时裂纹梁的固有频率曲线,并用Katz方法计算该频率曲线的分形维数(FD)曲线。数值计算结果表明:本文方法能够准确地检测出裂纹的位置以及损伤程度,并通过对裂纹深度、质量块大小与FD曲线峰值的关系进行详细分析,验证了移动质量法结合分形方法对损伤检测的有效性。
[1]Liang,R.Y.,J.Hu,and F.Choy,Theoretical study of crack-induced eigenfrequency changes on beam structures [J].Journal of Engineering Mechanics,1992 ,118(2):384-396.
[2]Messina,A.,E.Williams,and T.Contursi,Structural damage detection by a sensitivity and statistical-based method[J].Journal of Sound and Vibration,1998.216(5): 791-808.
[3]Pandey,A.and M.Biswas,Damage detection in structures using changes in flexibility[J].Journal of Sound and Vibration,1994.169(1):3-17.
[4]董五安,杨世浩.频率变化平方比向量确定结构损伤位置[J].噪声与振动控制,2013,03:226-230.
[5]ZHON Shun-cong and Oyadiji S O.Identification of cracks in beams with auxiliary mass spatial probing by stationary wavelet transform[J].Journal of Vibration and Acoustics,2008,130(4):1-14.
[6]聂彦平,毛崎波.基于PVDF传感器和工作曲率变形实现裂纹梁裂纹检测[J].传感技术学报,2012,26(1):138-142.
[7]ZHON Shun-cong and Oyadiji S O.Analytical predictions of natural frequencies of cracked simply supported beams with a stationary roving mass[J].Journal of Sound and Vibration,2008.311(1):328-352.
[8]Low K,On the eigenfrequencies for mass loaded beams under classical boundary conditions[J].Journal of Sound and Vibration,1998,215(2):381-389.
[9]Mandelbrot,B.B.,How long is the coast of Britain[J].Science,1967.156(3775):636-638.
[10]EstellerR,Vachtsevvanoxs,EchauiJLiltB.A comparisonoffractaldimensionalgorithmsusing synthetic and experimental data[J].Circuits and Systems, 1999(3):199-202
[11]Hadjileontiadis L,Douka E and Trochidis A.Fractal dimension analysis for crack identification in beam structures[J].Mechanical Systems and Signal Processing, 2005,19(3):659-674.
Damage Detection for Cracked Beams by UsingAuxiliary Mass Approach Combined with Fractal Dimension Method
CHEN Xiao-chao,MAOQi-bo
(School ofAircraft Engineering,Nanchang Hang Kong University,Nanchang 330063,China)
Taking a cracked simply supported beam as an example,a new approach based on auxiliary mass combined with fractal dimension analysis is proposed for damage detection.When the auxiliary mass is mounted at different locations of the beam,the natural frequencies of the beam-mass system are changed.So,when the auxiliary mass transverses from one end of the beam to the other,a set of curves of the natural frequencies of the beam-mass system can be obtained.Then the fractal dimension method is imposed to analyze the natural frequency curves,and the location and depth of the crack can be detected.Furthermore,the effects of the auxiliary mass and the parameters of fractal dimension on the accuracy of the damage detection are investigated in detail.The simulation results demonstrate the efficiency and accuracy of the proposed method.The main advantages of the proposed method are that there is no need of the structural mode information and it can be realized in arbitrary excitation environment.
vibration and wave;auxiliary mass;natural frequency;fractal dimension;damage detection
1006-1355(2014)03-0155-05
TH16;TB123
A
10.3969/j.issn.1006-1335.2014.03.033
随着现代工程结构的不断大型化和复杂化,损伤识别与检测技术对保证结构完整性和安全性具有越来越重要的意义。根据动力学基本理论可知,当结构某一部位产生损伤时,在物理空间中表现为刚度下降、柔度增大;在模态空间中表现为固有频率降低,阻尼比增大,振型发生变化。
2013-06-25
国家自然科学基金(51265037);江西省高校科技落地计划项目(KJLD12075);江西省教育厅科技项目(GJJ13524)
陈小超(1988-),男,硕士研究生,目前从事基于振动的结构损伤检测方向的研究。
E-mail:keithiscxc@gmail.com

