基于能量法的库伦摩擦阻尼特性分析

石慧荣，李宗刚，张军平

（兰州交通大学，兰州730070）

基于能量法的库伦摩擦阻尼特性分析

石慧荣，李宗刚，张军平

（兰州交通大学，兰州730070）

为了研究摩擦减振特性，对给定二自由度摩擦系统的动力学方程进行分析，利用能量守恒原理和阻尼减振原理给出系统摩擦阻尼的损耗因子。通过分析不同外载荷、质量比和刚度比对损耗因子的影响，以及对不同最大动摩擦力时质量体的长、短时程位移变化特性进行比较。结果说明损耗因子随外载荷和系统结构参数不断变化；最大损耗因子对应的最大动摩擦力作用系统，只有在短时间内有较好的减振特性，在实际中可以采用主动控制摩擦力的方法达到最佳减振效果。

振动与波；摩擦阻尼；减振；损耗因子；能量法；

目前大多数的研究主要是对摩擦阻尼模型的数值求解，分析系统的振幅、速度和加速度变化情况，而利用能量法对摩擦阻尼损耗的研究还比较少，本文应用Runge-Kutta法对二自由度模型进行求解，将能量法与粘弹性材料损耗因子的定义相结合，给出摩擦阻尼损耗因子，分析其应用范围和影响摩擦阻尼特性的结构参数，为工程实际提供参考。

1 二自由度摩擦阻尼模型

二自由度模型如图1所示，假定摩擦表面的摩擦系数为定值，最大静摩擦力与滑动摩擦力相等。M1和M2分别表示物块1和2的质量，K1、K2和K3分别为弹簧刚度系数，U1和U2表示物块的位移，Fs为最大静摩擦力。弹簧1作用力小于Fs时，摩擦副锁死，大于Fs时系统有能量损耗，摩擦力Fs作功，所以引入函数Fsgn。

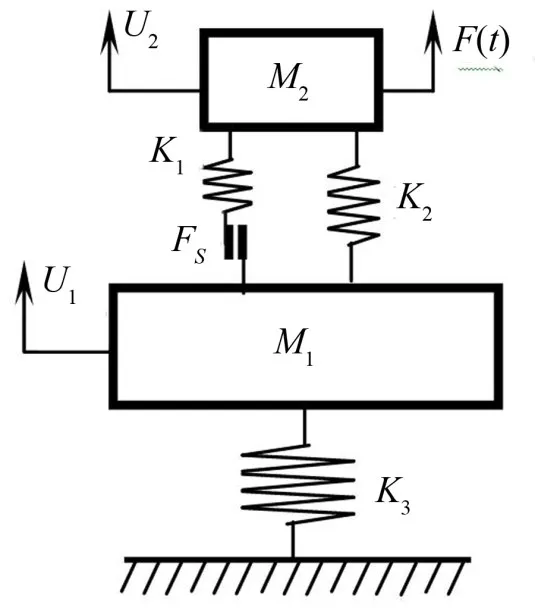
图1 二自由度模型

同时考虑到摩擦力始终与速度方向相反，引入符号函数sgn(·)，则系统的运动方程可以表示为

当Fsgn=-1时，系统为简单的二自由度无阻尼弹性系统，方程存在简析解；当Fsgn=1时，摩擦副“解锁”，系统为非线性动力学方程，摩擦副滑动位移S表示为

利用Runge-Kutta法对方程（2）和（3）进行求解，设X=U˙1，Y=U˙2，则有

2 摩擦阻尼损耗因子

对于图1二自由度模型，振动系统的能量损耗主要是摩擦损耗，根据能量守恒原理总机械能耗散等于摩擦力所作的功，可以定义摩擦阻尼损耗因子。但由于自由振动系统的摩擦力作功随时间变化逐渐减小，而且不同系统运动特性不同，所以取一个周期内能量损耗来计算损耗因子，损耗因子可以表示为

其中ΔE为一个周期内摩擦耗散的能量，E为系统初始的总能量，η为二自由度系统损耗因子。

根据动能定理，二自由度摩擦阻尼模型全部能量损耗来自摩擦力所作的功，因此有

其中E1为系统初始施加作用力后的平衡态时的总机械能，E2为经过一个周期2 π/f后的剩余机械能，ST为一个周期内总滑动位移。

3 二自由度模型振动特性分析

二自由度摩擦阻尼系统在运动过程中，摩擦副一般总是由“解锁”到“锁死”变化，此时系统方程也由非线性转变为线性，而对于线性系统不具有阻尼性能，所以对摩擦损耗因子分析都在摩擦副“解锁”范围计算。下面以第一个周期内能耗进行估算，分析二自由度系统损耗因子的应用特性和质量比、刚度比变化对损耗因子影响。

3.1 摩擦阻尼损耗因子特性

初选M1=1 Kg，M2=2 Kg，K1=10 000 N/m，K2= 20 000 N/m，K3=20 000 N/m，首先对模型施加F（t）= 1 800 N的恒力，使系统具有初始势能E1，然后释放物块1，在每次自由振动过程中调节一次Fs大小。系统在摩擦副锁死时的固有频率分别为f1=12.47 Hz和f2=35.18 Hz，以第一模态的周期0.080 1 s内的能量损耗计算损耗因子。

损耗因子随摩擦力的变化情况如图2所示，由图可以看出损耗因子随摩擦力增大先增加后减小，最大值出现在Fs=300 N时，其对应的损耗因子为0.135 36，此时假定初始状态摩擦副锁死可得弹簧1受到瞬时最大作用力为600 N，而动摩擦力Fs恰好为二分之一弹簧载荷。而且当Fs达到600 N时，由于质量块存贮能量，摩擦副未锁死，此时的损耗因子为0.106 9，只有动摩擦力Fs达到五倍的最大阻尼值对应摩擦力1 500 N时，摩擦副才可能弯曲锁死，此时损耗因子才近似为零。

图2 损耗因子变化曲线

当选取不同摩擦力时，U2在短时程响应如图3所示，可以看出在0.7 s内，Fs=300 N时对应的U2缩减最快。但是当时间较长时，摩擦阻尼减振情况会发生变化如图4，（a）、（b）和（c）分别表示Fs=30 N、300 N和900 N在3.5 s内的时域变化情况，从图中可以看出Fs越小摩擦损耗因子也比较小，但摩擦副滑动位移S越大，在整个时段内摩擦力做功最多，减振效果也最好，而Fs为300 N时，虽然开始能够使振幅衰减最快，但随着机械能快速减少，弹簧1的弹性变形力迅速变小，当小于Fs时系统锁死，滑动副位移S为零，变为无阻尼系统，振幅几乎不再减小，而且Fs越大，长时程的减振效果也越差。

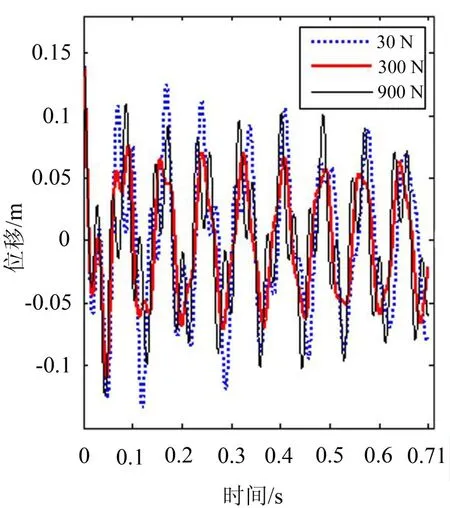
图3 短时程时域响应

图4 长时程时域响应和摩擦副位移

由上可知，对于摩擦阻尼损耗因子只有在摩擦副不发生“锁死”的情况下能够反映摩擦阻尼的减振性能，随着能量的损耗K1|U1-U2|逐渐减小，摩擦副滑动位移S随之减小，最后导致K1|U1-U2|＜FS时摩擦副“锁死”，系统变为保守系统维持恒定振幅。同时损耗因子主要反映摩擦阻尼在短时程内的减振性能，所以可以依据max(K1|U1-U2|)及时调整Fs，使系统减振特性在整个时域达最好。

3.2 系统参数对损耗因子影响

二自由度系统损耗因子不仅随外部载荷F(t)和动摩擦力Fs变化，而且还受到系统质量和刚度的影响。在下面的分析中M1和K1与前面分析相同，外载荷F(t)=1 200 N，改变其它参数来分析损耗因子的变化情况。

如图5所示，刚度系数不变，M2的变化不影响损耗因子曲线变化趋势，当M2增加时损耗因子逐渐变小，但是由于M2较大时贮存和吸收更多的能量，在Fs较小时损耗因子上升放缓，较大时下降速度变慢。同时注意到最大损耗因子对应的摩擦力Fs不受质量图2影响。损耗因子最大处，无摩擦副时簧1的最大作用力为400 N，损耗因子最大点对应的Fs= 200 N，1 000 N时损耗因子近似为零，与前文分析一致。

图5 质量比对损耗因子影响

其它参数不变，刚度系数K2变化对损耗因子的影响如图6所示，当K2增加时，损耗因子也随之增加，损耗因子最大点对应的动摩擦力Fs也逐渐增加，而且K1/K2越大，损耗因子曲线变得越平缓。图7为K3变化时损耗因子的变化曲线，由图可见K3增加时，损耗因子逐渐减小，K3越大对应的损耗因子曲线变化也越平缓，但损耗因子最大点对应的动摩擦力Fs不变。

由上面的分析可以看出，M2/M1和K1/K3的改变不影响最大损耗因子对应的动摩擦力Fs与无摩擦弹簧1最大作用力的比例关系，而K1/K2增大会使这一比例逐渐减小。对图1所示结构，弹簧1和2并联，再与3串联，结合上面的分析可以得出，要想提高结构的减振性能，可以将串联结构刚度选的小一些，将并联部分的刚度取大些，同时不能使M2太大。

4 控制摩擦力减振

图6 刚度K1/K2对损耗因子的影响

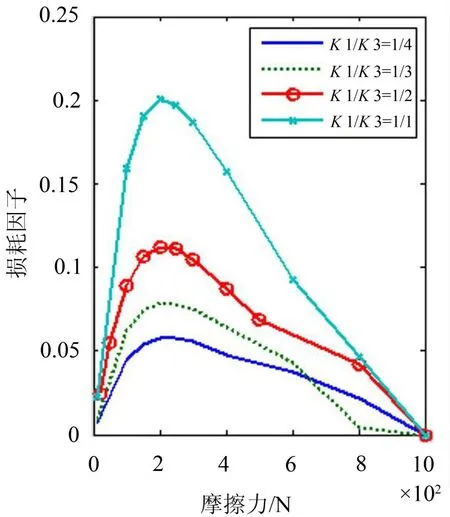
图7 刚度K1/K3对损耗因子的影响

对于给定的系统属性改变比较困难，调整最大静摩擦力可以通过调整正压力和摩擦表面接触形式实现，而动摩擦力Fs对机械能损耗影响较大，依据前面的分析，在应用中可以根据检测弹簧1最大作用力改变摩擦力以达到最大损耗因子。针对3.2节给定的系统，保留所有结构参数不变，在2 s内改变采样时间Δt，使最大动摩擦力FS=max(K1|U1-U2|)/2，比较U2的时域变化特性。

由图8与图2相比可以看出，采用控制摩擦力方式要比恒定摩擦力减振更加有效。图8中Δt分别为0.133 s，0.08 s和0.05 s时，在整个时程内摩擦力和滑动位移由于能量不断损耗，随着U2振幅减小而逐渐减小；位移U2在Δt=0.08 s时衰减最快，此时调控时间Δt刚好为该二自由度系统模态一对应的周期。Δt大于周期时下一周期内滑动位移S迅速减小，系统的能量损耗也随之减小，所以减振效果较差；Δt小于周期时摩擦力的最大耗能还没有达到就改变摩擦力大小，也会导致减振不能充分发挥。实际控制中由于摩擦阻尼的存在，系统的周期在随摩擦阻尼变化，因此Δt应该适时调整以达到最佳的减振目的。

图8 不同Δt时的时域相应

5 结语

通过对二自由度摩擦阻尼结构的动力学特性的分析，应用能量法和粘弹性阻尼机理计算单个周期内的能量耗散，对比结构参数对损耗因子的影响，可以得出如下结论：

(1)摩擦阻尼可以在适当动摩擦力作用下达到最大值；

(2)最大损耗因子只在振动初期才能反映减振特性，随着能量耗散摩擦力减振结构将会很快锁死，失去减振作用，相反较低的摩擦力在长时程范围内有较好的减振效果；

(3)给定参数的二自由度摩擦阻尼结构，动摩擦力Fs与不考虑摩擦时弹簧1最大作用力达到一定比例时，损耗因子有最大值，这一比例与外载荷无关；

(4)M2/M1、K1/K3不影响结论3所述比例关系，K1/K2对其有较大影响；

(5)在工况允许的情况下，适当改变结构参数同样可以达到较好的减振效果；

(6)按周期段时长控制摩擦力能够获得良好的减振效果。

[1]Thomsen J J,Fidlin A.Analytical approximations for stickslip vibration amplitudes[J].International Journal of Non-Linear Mechanics,2003,38:389-403.

[2]Menq C H,Griffin J H,Bielak J.The influence of a variable normal load on the forced vibration of a frictional damped system［J］.ASME Journal of Engineering for Gas Turbines and Power,1986,108:300-305.

[3]漆文凯，高德平.带摩擦阻尼装置系统振动响应分析方法研究［J］.航空动力学报，2006，21(1)：167-173.

[4]Marcus A.Louroza,Ney Roitman,Carlos Magluta.Vibration reduction using passive absorption system with Coulomb damping［J］.Mechanical Systems and Signal Processing,2005,19:537-549.

[5]F.Weber,J.Høgsberg,S.Krenk Optimal tuning of amplitudeproportionalcoulombfrictiondamperfor maximum cable damping［J］.ASCE Journal of Structural Engineering，2010,136:123-136.

[6]马晓秋，王亲猛，张 锦，程 滔.带干摩擦阻尼结构叶/盘系统动力学分析［J］.航空动力学报，2002，17(1)：110-114.

[7]李中郢，卢正人.金属橡胶减振器组合刚度特性研究［J］.哈尔滨工业大学学报，2005，37(10)：1327-1329.

[8]王 睿，华宏星.变摩擦阻尼方法的建模与实验分析[J].噪声与振动控制，2011，31(4)：16-20.

Analysis of Damping Characteristics of Coulomb Friction Based on Energy Method

SHI Hui-rong,LI Zong-gang,ZHANG Jun-ping

(Lanzhou Jiaotong University,Lanzhou 730070,China)

To study friction damping characteristics,a dynamic equation of two-DOF friction system is analyzed.Based on the principle of conservation of energy and the principle of damping,the loss factor of the friction damping system is defined.The system loss factors are analyzed for different mass ratio,external load and stiffness ratio.The displacement characteristics for long and short periods are compared for different maximum dynamic frictions.The result shows that the loss factor changes with varying of the external load and system parameters.And the system with the maximum dynamic frictional force corresponding to the maximum loss factor has good damping characteristics only in a short period of time.The active control of friction can be used to achieve the best damping effect.

vibration and wave;friction damping;vibration reduction;loss factor;energy method

1006-1355(2014)03-0042-05

V231.9

A

10.3969/j.issn.1006-1335.2014.03.009

在现代工业生产中，振动控制一直都是一个重要课题，而由于摩擦对机械能耗散作用，摩擦减振被广泛应用于机械制造、航空发动机、土木工程等领域，所以对摩擦阻尼特性的研究具有重要意义。

摩擦接触为一种复杂的非线性接触，为了能够准确分析摩擦与振动之间的关系，已经有许多学者对其进行分析，并提出了一些数学模型[1―3]，应用这些模型研究振动中摩擦阻尼的作用，对工程实际具有很好的指导作用。Marcus A.Louroza等[4]分析了被动二自由度减振结构质量比和摩擦力对摩擦阻尼特性的影响；Weber等[5]依据线性粘性阻尼原理建立了缆索结构的库伦摩擦阻尼模型，并对缆索上阻尼器位置进行了优化，实验证明其具有良好的减振性能；马晓秋等[6]研究了干摩擦阻尼作用下叶盘系统的振动特性，提出了优化摩擦阻尼概念；李中郢等[7]指出金属橡胶本身就是一种摩擦阻尼材料，并利用能量法对组合金属橡胶的应用特性进行了研究；王睿等[8]提出了一种自适应摩擦调整阻尼减振方法，并对其有效性进行了验证。

2013-07-08

兰州交通大学青年科学基金项目（基金号：2012014）

石慧荣（1979-），男，博士研究生，主要研究机械振动控制，机械动力学优化。

E-mail:shrz98@aliyun.com；