正确分析：初中数学应用题解题教学的关键

缪晓菊

[摘 要] 分析能力是人类五大基本生存能力的基础，是处理外界表象、总结客观规律的根本方式. 初中数学应用题教学是培养学生实践能力、分析能力和知识应用能力的重要知识载体，而正确地分析和思考又是成功解答应用题的核心条件，所以，笔者将着重探讨初中数学应用题解题教学中具体应当如何发挥学生的分析能力.

[关键词] 初中数学；应用题；解题教学；分析

通俗地讲，分析是指科学剖析整体的部分形态，以探寻其存在的基本规律和联系的一种科学思维活动. 而由分析产生的大脑分析能力，指的是将某种表象或概念根据一定的原则，分解成比较直观和简单的部分，再从这些部分中思考、探究、分辨，以获得它们之间的基本规律和联系，进而解决整体性问题的一种能力. 分析能力作为人类生存和发展的五大基本能力的基础，是每一个正常的个体都必须培养的一个基本素质和技能. 初中数学应用题是实际问题、既定数学知识、解题方法、计算训练等多种数学能力的综合体，这种复杂的问题必然需要学生发挥自身的分析能力，让分析带动大脑思考，让思考厘清应用题的基本数量关系，进而得出应用题的解题思路. 而且，初中生的思维和大脑发育正处于激烈转型的阶段，此时对其进行必要的思维训练和分析能力培养，是其更好地学习数学的关键所在. 因此，初中数学应当充分利用应用题解题教学的契机，将分析能力的培养深深地灌入其中，让学生实现分析能力与应用题学习的双重发展.

内驱力：唤醒学生主体精神的

回归

分析思考是个体有意识的主观思维活动，是个体自觉自愿的一种认知冲动，任何一个外在的个体都无法强迫一个不愿进入分析的人进行主动的思维过程. 但很多初中数学教师天真地认为自己的思想和意志能够代替学生进行数学分析和思考，从而阻碍学生主体精神和自觉意识的表征. 所以，对于实际操作性较强、综合理解能力和分析能力要求较高的应用题来说，破除这层教学坚冰，还给学生解答应用题的主体地位，学生才能充满分析的内驱力，才能主动地投入解题实践和思考中. 一方面，初中数学教师要学会转换角色，将解题的自主权归还给学生，并为学生创造应用题分析的和谐情境，以自主性解题的新方式带动学生主体性的觉醒，从而激发学生向往成功解题的内驱力. 另一方面，期望效应指出，赏识、激励和期望是焕发学生学习内驱力的最佳方式，初中数学教师除了“简政放权”外，还应根据不同学生的解题需要，给予适当的赏识和激励，以此进一步调动学生解题的主动性.

例1？摇 教学“正弦、余弦”时，教师为学生出示了一道实际应用题，如下：

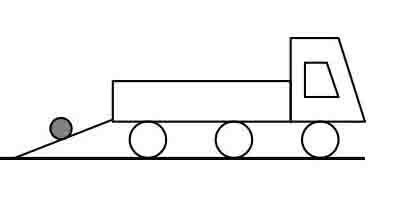
为了节省搬运的力气，芳芳的爸爸在装运货物时，拿了一块铁板架在了车与地板之间，如图1所示. 已知这块铁板的长度为5 m，货物从地板滑到车厢的水平距离为3.6 m.

（1）这块铁板与地面的夹角是多少？

（2）车厢与地面的水平距离是多少米？

（可借助计算器，结果保留两位小数）

分析？摇 这是一道典型的实际应用题，是将正弦、余弦与实际问题联合起来而创设的一个旨在锻炼学生综合运用正弦定理和余弦定理解题的实践模型，但要想成功解答出本题，还必须充分发挥学生的分析能力，因为无论是解题思路还是计算流程，对于学生来讲，都比较复杂. 所以，如果学生的主体性精神没有获得觉醒，缺乏进行主动分析的意识和能力，坐等教师给予现成的解题思路，并在学生解题后提供答案以比对，那学生永远不会知道自己到底“会不会”“能不能”. 因此，要想引导学生正确地解答出本题，关键在于学生要具有思考和分析的内驱力，要将解答本题看成是自身的一种责任或挑战. 初中数学教师应当将占据许久的这种能力还给学生，并适当以奖励性措施作为成功解题的诱因，为学生创设一个解题实践竞赛的平台.

助推力：注重学生思维品质的

培养

从解题的范围和过程来看，分析是一种偏向于综合性思维认知的活动，分析所指的对象非常广泛，即要连结自身已有的学习基础和生活经验，又要把握住当前所学的基本数学知识，而且，从唯物主义认识论来看，分析是人类的一种意识活动，但意识并不总是正确的，有时候也会由于出现分析错误而导致解题走入误区，因此，这就需要一个良好的思维品质做伴，以思考题目需要具备哪些基本条件，需要联系哪些基本知识，并判断自己分析的结果是否合乎题目条件的要求等.

例2 学习“解直角三角形”时，要解答实际问题：

有这样一块田地，它呈梯形形状，上底为20 m，高大约为5 m，梯形的坡面与下底所成的角分别为30°和55°，现由于修路需要占用，土地局工作人员需求出它的面积，以商量补偿事宜，你知道怎么求吗？

分析？摇 学生一拿到这道题，不是要立即对题目进行分解和剖析，而是要先思考本题真正要求的量是什么. 由问题“梯形的面积”，学生可以联想到梯形的面积公式，但看到题目的条件非常多，且比较复杂，学生可以思考是不是可以通过画图来帮助解题分析，于是，思考到这里时，学生可以马上绘画简图，以帮助分析题目中条件的关系，最终确定解题的关键在于“求出下底的长度”，而上底已知，分别作高后，则将求下底变成分别求两个直角三角形的一条直角边.

其实，思考与分析是并驾齐驱的思维活动，有分析就会伴随思考，有思考也会伴随分析，因此，发展学生的分析能力时，也应培养学生的思维品质.

主渠道：加强学生解题实践的

训练

人的分析能力是与生俱来的，是潜藏在我们脑海中的一种基本能力，但它并不会主动外显出来，更不会在无意识控制下进行自发式的发展，它需要个体在不断的实践和经验积累中，慢慢得到开发和修正. 所以，虽然初中生的分析能力已有初步发展，但这个年龄正是培养分析能力的大好时期. 初中数学教师应当用好应用题解题实践这把利刃，让其割开学生心中的那份隔阂，让学生的分析能力在解题实践中得到充分展示和发展.

例3？摇 学习“一元二次方程”时，这一章节主要是向学生介绍一元二次方程的基本结构以及成立的基本条件，并引导学生学会利用一元二次方程解答实际问题，将数学知识与实际问题进行完美结合，所以，本章节所学知识的落脚点应当放在学生的知识应用上. 但一元二次方程的实际应用题并不是唾手可得的，如何设置未知数、如何确定题目的等量关系、如何正确列出方程以及确定最终的解等，都需要学生有一个清醒的头脑，即要有一个能够作出正确判断和分析的思维能力. 所以，初中数学教师在教学本章节时，除了要向学生精教本课的基本知识外，还应当将教学的重点放在实际的解题操练中，让学生在不断的训练中厘清思维障碍，掌握分析的基本技巧和能力，让一元二次方程应用题成为学生分析能力培养的“孕婴所”.

保障性：学会反思应用题解题

范式

应用题是一种比较复杂的数学问题，所涉及的知识内容较为综合，而且初中生正处于青春发育时期，冲动、粗心、着急等心理有时候会造成初中生的错误分析，从而影响整道题的解题情况，这就需要学生养成一个反思分析的良好习惯，且反思分析还能帮助学生更好地总结应用题解题规律，归纳应用题解题题型，熟悉应用题解题的基本方法和步骤等.

仍以例2为例，学生虽然能够正确分析并解答出题目，但这不代表学生在解答本题时就是完美无缺的，学生应当充分利用自己细心的思维特征，反思自身的解题过程和思路，看看有没有哪些环节是多走弯路或犯错的，分析解题中是否存在单位忘写、该“答”未“答”的情况等，总之，学生要利用逆向分析来检验自己的解题过程，培养仔细认真的思维习惯. 另外，学生还应通过分析来总结解决此类问题的一般范式，如出示夹角与直角边，必然与“解直角三角形”存在关联等，以简化以后解题分析的前奏过程，直截了当地进入解题中心.

总之，分析能使我们认清世间的万事万物，行使我们躯体官能所具有的基本能力，也能使我们的思维和意识得到不断地发展和强化，不至于止于静止的无生命状态. 而初中数学应用题解题是一种思维认知活动与实践应用的结合，更加需要学生分析能力的参与和作用，这样才能明辨其中的数学原理，得出最为基本的解题策略和思路.