基于层次分析法的配送中心选址模糊综合研究述评

杨 静

（三江学院，江苏 南京 210012）

在现代连锁企业中，选取恰当的配送中心位置是保证配送速度和质量、提高客户服务水平的重要环节。配送中心拥有众多机械设备，一旦建成就很难改变，所以选址不当将付出很大的代价。鉴于此，本文综合学者相关研究，并运用改进的层次分析法和两级模糊评判的方法进行配送中心的优化选址。

一、影响因素分析综述

关志民,周宏波,马钦海在《基于模糊多指标评价方法的配送中心选址优化决策》一文中指出，“建立配送中心选址评价指标体系，应从宏观环境、交通状况、经济性”三个“方面进行综合评价，每个方面又建立各自的次一级指标。宏观环境包括政策法规和自然环境与地理条件。政策法规指地方政府对行业发展的激励措施、税收情况；自然环境与地理条件指水文、地质、气象以及地形状况。”1东北大学学报［J］.2005,（8）.

关于交通状况，王献锋在《物流选址评价指标体系的设计》指出，“交通状况指标包括运输时间、运输可能度、运输便利性和公共设施。运输时间：运输时间是物流配送中最关键的一点，及时将物品送到客户的手中是衡量物流的一个重要指标。路况越好，运输时间越短，物流反应速度也快，物流效率也就越高。运输可能度：运输可能度反映了交通拥挤程度。运输便利性：主要是指方便的交通运输条件。公共设施状况：既要求城市道路、通信等公共设施齐备，还要求供电、供水、供热和燃气充足，要有排污能力和废弃物处理能力。”2中国商贸［J］.2011,（7）.

关于经济性指标，王献锋在同文中指出，“投资收益率：建立物流配送中心，最终的目标是为了盈利，所以考虑是否建立物流配送中心，主要考虑其投资是否能有所收益，收益率越高，则利润越高。物流费用：物流费用是配送中心选址的重要考虑因素之一。不同的地区，因为路况或是当地经济发展状况等方面的原因，其管理运营费用有所不同，在对物流选址的过程中，尽量选择那些运营费用较低的地方设立配送中心。劳动力条件：该场区应该拥有充足的、素质较高的劳动力。平均地价因素：一般占地面积较大，地价的高低对其区位的选择有重要影响。发展潜力：主要是指当地物流发展状况，发展潜力越大，就越应该在当地建立配送中心。”3同2.

综合上述学者的分析，每个企业在配送中心选址的过程中可以根据实际情况增减相应的指标。

二、指标权重的确定述评

1、建立决策层次结构模型。在对配送中心评价因素分析的基础上，建立层次结构模型如图1所示：配送中心最佳位置（R）为目标层；衡量配送中心选址好坏的三个基本因素（S）为准则层；衡量各准则层的影响因素（P）为指标层；备选的配送中心位置（C）为方案层。

3、求拟优一致阵

通过求拟优一致阵的概念，对AHP进行改进，使之自然满足一致性的要求。算法如下：

（1）计算反对称矩阵 C=（cij）m×m，其中 cij=lgbij，则

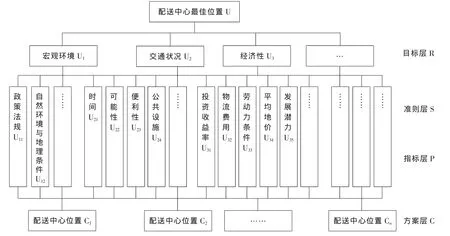
图1 层次结构分析模型

2、判断矩阵的构造。构造判断矩阵通常采用美国运筹学家萨迪（A.L.Saaty）提出的9标度法，对于进行配送中心选址，在判断过程中存在着一定的复杂性和模糊性，如在指标层中时间性和便利性的相对重要程度往往难以把握。为此，采用三标度法来解决这一问题。

（1）建立三标度比较矩阵 A 为（aij）n×m（i，j=1，2，…，m）。其中aij定义为：

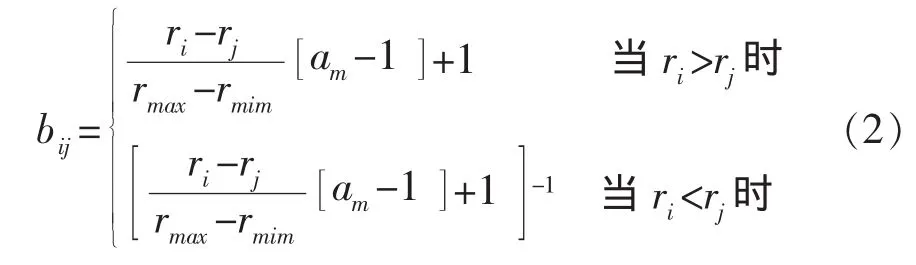
最优传递矩阵 D=（dij）m×m，中：

（2）构造拟优一致阵 B*=（bij*）m×m。 显然，由第（2）步得到的判断矩阵B是互反矩阵，C=lgB是反对称矩阵。

4、层次单排序

其表达式为：

式中：λmax——判断矩阵B*的最大特征根；

W——对应于 λmax的特征向量（W1，W2，…，Wn）T。经归一化后，其分量各值即为元素 B1，B2，…，Bn在对应上层元素Ak下排序的权重。5戴英姿，马啸来.配送中心选址方案的综合评价方法J］.石家庄铁道学院学报，2004(3）：93-96.

5、逐层聚合计算层次总排序权重

按照从上而下的逐层计算，假定我们已经计算出第K-1层m个元素对于总目标的相对权重向量Wk-1=（W1k-1，W2k-1，…，Wmk-1）T。 第 K 层 n 个元素在第K－1层的第j个元素作为准则下的排序权重向量为：

则第K层的第i个元素对于总目标的相权重Wik：

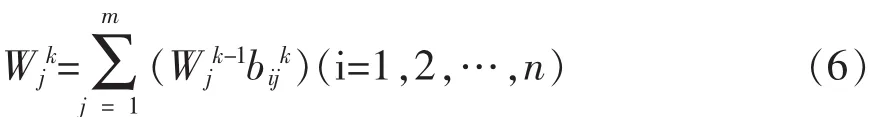
则第K层n个元素对于总目标的组合排序权重向量为：

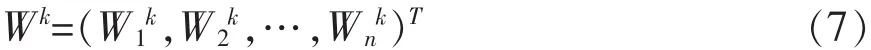
依此类推，即可求得方案层的各方案对总目标的优先级排序总权重。

三、模糊综合评价

由于配送中心的选址的过程是多属性的决策问题，具有明显的模糊特性。因此本文采用模糊综合评价法对备选方案进行评价。具体步骤如下：

1、确立配送中心选址价值指标

在改进的AHP法确定评价指标权重的基础上，将配送中心位置划分为五个等级：适宜、较适宜、一般、不太适宜、不适宜。其中目标层U作为评价对象集，基准层Ui作为一级评价指标集合，指标层Uij为二级评价指标，配送中心位置级别划分作为评语集 V＝{v1，v2，v3，v4，v5}＝{适宜，较适宜，一般，不太适宜，不适宜}。

2、构造隶属度函数

隶属度是指各分类指标从属于某种评价类别的程度的大小，一般采用调查统计法确定。6张学成，何去非.基于 AHP-GP 的物流中心选址方法［J］.重庆工学院学报，2007，（9）：111-113.

3、一级综合评价

由上分析计算知： 评语集 V＝{v1，v2，v3，v4，v5}＝{适宜，较适宜，一般，不太适宜，不适宜}，Ui中各元素相对 Ui的权重为：Wi=（Wi1，Wi2，…，Wij）。 设 Ri为Ui到V的模糊评判矩阵，

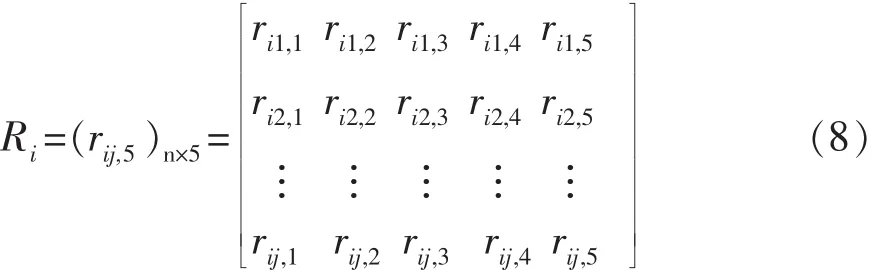
其中：j为Ui中影响元素的个数，rij,k为因素Uij对应vk的隶属度。

则Ui的一级综合评判向量Pi为：

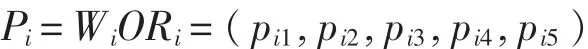
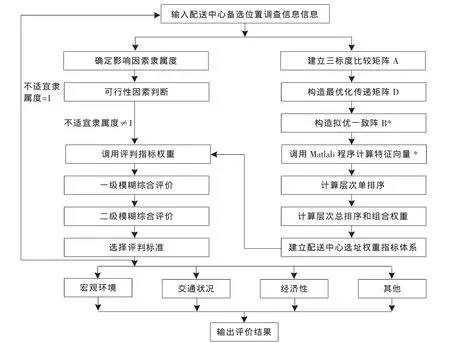
图2 计算程序流程

四、二级综合评价

因为每个Ui都是影响配送中心选址适宜度的一个指标，归一化后的Pi作为评价对象集U的单因素向量，可构成U到V的模糊综合评判矩阵：

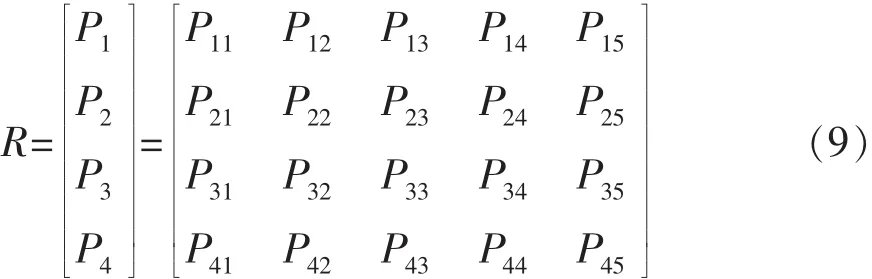
于是二级综合评判向量为：

P＝WOR＝（P1，P2，P3，P4，P5）

算子说明：

模糊算子有多种可选，为了提高计算的精确度，可以采用加权算子。

第一级综合评判模型为：

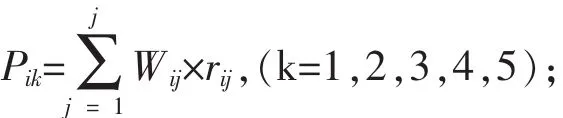
第二级综合评判模型为：

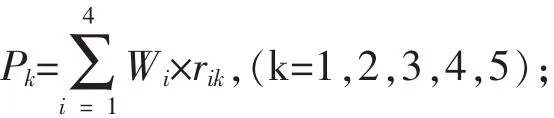
五、评价模型程序化

层次分析法和模糊综合评价的计算过程比较复杂，采用人工计算非常费时，因此将上述配送中心选址问题利用计算机编程实现，流程如图2。

［1］郑勋，杨家其.配送中心选址的理论原则与优化方法［J］.交通科技，2001，（6）：54-56.

［2］韩利，梅强.AHP-模糊综合评价方法的分析与研究［J］.中国安全科学学报，2004,（7）：86-89.

［3］戴英姿，马啸来.配送中心选址方案的综合评价方法［J］.石家庄铁道学院学报，2004,（3）：93-96.

［4］王晓博，李一军.电子商务企业配送中心选址评价指标体系及模糊综合评价［J］.商业研究，2006,（10）：56-59.

［5］张学成，何去非.基于 AHP-GP的物流中心选址方法［J］.重庆工学院学报,2007,（9）：111-113