Picard定理的一个教学注记

刘芝秀，易 敏

（南昌工程学院 理学系，江西 南昌 330099）

Picard定理的一个教学注记

刘芝秀，易 敏

（南昌工程学院 理学系，江西 南昌 330099）

在复变函数教学过程中一般都含有对著名的Picard大定理和小定理的介绍，甚至证明过程，但若未能明确指出Picard大定理与小定理的等价性，学生容易产生Picard小定理不蕴含大定理的错误猜测，这不利于学生对Picard定理以及学科发展的了解，它们其实是同样深刻的等价定理。该文旨在强调这一点，并利用正规族理论中的Zalcman-Pang引理证明了Picard大定理和小定理的等价性。

Picard定理；亚纯函数；正规族；模分布

0 引言

Picard定理是复分析中著名且深刻的结论，是亚纯函数值分布方面的代表性结果，是复分析发展的一个重要原动力，证明它们产生了许多思想方法[1-3]。因此，大部分复分析方面教材（即使是入门教材）都对Picard定理进行了介绍。所以，在教学过程中也应该特别注意对Picard定理的介绍讲解，应紧随学科的发展状况。它通常包含两个定理：

Picard小定理：若整函数f(z)不取两个复值a,b(a≠b)，则 f(z)为一个常数。

Picard大定理：解析函数在本性奇点的空心领域内无穷多次地取到每一个有穷复值，至多可能除去一个例外值。

这两个定理在形式上差别甚大，人们分别冠名于Picard“大”定理与“小”定理。同时，也有部分文献笔误为Picard大定理是Picard小定理的推广，是更强更深刻的结论。本来又有“大”定理与“小”定理的名称之别，这在教学过程中，较容易给学生以错觉，影响教学工作。事实上，这两个定理是完全等价的。

明确这一点，得益于亚纯函数正规族理论的发展，特别值得一提的是我国数学工作者对正规族理论的发展做了较多突出的贡献[4-7]。正规族理论也有许多的应用。例如，在模分布中的应用研究就很活跃[8-11]，下文将利用正规族理论证明著名的Picard大小两定理的等价性，这也正好表明了正规族理论在亚纯函数值分布中很具有应用价值。更多关于正规族的概念和相关理论可参阅文献[7]，下面仅叙述其中的两个引理。

1 引理

引理1[7]设{f(z)}为区域D内的亚纯函数族，这个族在D内正规的充要条件是它在D内每点正规。

引理2[12-13]（Zalcman-Pang）设{f(z)}为区域D内的亚纯函数族，δ：-1＜δ＜1 为任一实数。族{f(z)}在某点Z0∈D正规的充要条件是存在一列函数fn(z)∈{f(z)},存在一点列zn→z0及一正数列tn→0，使函数列t-δnfn（zn+tnz）fn（z）∈{f(z)}在C上内闭一致收敛于非常数亚纯函数g(z)。

2 等价性证明

2.1 Picard大定理证明Picard小定理：

设f(z)为一整函数，且不取a，b。

（1）若 0 是 g（w）的可去奇点，则 g（w）可解析开拓至扩充复平面C，即有f(z)=g（w）为常数。

（2）若 0是 g（w）的 m≥1 级极点，设 g（w）=++c0，cm≠0,则 f(z)=cmzm+…+c0,这与 f(z)不取 a，b 矛盾。

综上所述f(z)为常数。

2.2 Picard小定理证明Picard大定理

2.2.1 Picard小定理证明Montel正规定则

Montel正规定则设{f(z)}为区域D内的全纯函数族，若对于族中每个f(z)在D内恒有f(z)≠0和f(z)≠1，则全纯函数族{f(z)}在区域D内正规。

证：假设{f(z)}为区域D内不正规，由引理1可设在Z0∈D不正规。

则由引理2并取δ=0可得，存在一列函数fn(z)∈{f(z)}，存在一点列 zn→z0及一正数列 tn→0，使函数列fn(zn+tnz)在C上内闭一致收敛于非常数亚纯函数g(z)。

由于fn(zn+tnz)为全纯函数，所以g(z)为整函数。根据 Hurwitz定理，因为 fn(zn+tnz)≠0和 fn(zn+tnz)≠1，所以g(z)≠0和 g(z)≠1，则由 Picard小定理得 g(z)=常数，矛盾。

2.2.2 Montel正规定则证明Picard大定理

设f(z)在z0有一个本性奇点，不妨设z0=0否则考虑函数f(z+z0)。假如存在R，使得有两个数不在{f(z)：0＜|z|＜R}中，我们将得到一个矛盾。

假如 f(z)≠α，f(z)≠β，0＜|z|＜R，不妨设 α=0，β=1（否则考虑）,设 G=0：0＜|z|＜R。

定义：fn：G→C 为 fn(z)=(),所以每个fn都是解析的，且都不取0和1，由Montel正规定则，{fn}在G中是正规的。

设{fnk}是{fn}的一个子序列，fnk→φ 在{z：|z|=R}上是一致的。其中φ或者在G内是解析的，或者φ=∞。

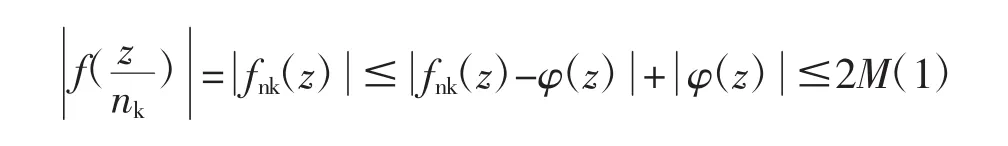
所以至多有一个复数w1不被f取到。下面再证w2≠w1，被f无穷次取到。若w2只被f有穷多次取到，那么取充分小圆，即得到一个无心圆，在这个无心圆内，f不取到 w1、w2两个值，矛盾。

[1]L.V.Ahlfors.Complex analysis[M].China Machine Press,2004.

[2]S.Gong.Concise complex analysis[M].University of Science&Technology China press,2009.

[3]J.B.Conway.Functions of one complexvariable[M].Berlin：Springer-Verlag,2004.

[4]L.Yang.Value Distribution theory [M].Spring-verlag Belin,1993.

[5]Y.X Gu.Normal family of meromorphic functions[M].Chengdu：Sichuan Education Press,1988.

[6]J.Schiff.Normal families[M].Berlin：Springer-Verlag,1993.

[7]Y.X.Gu,X.C.Pang,M.L.Fang.The theory of normal family and its application[M].Beijin：Sciencep,2007.

[8]M.L.Fang.A note on a problem of Hayman[J].Analysis,2000,20(1)：45-49.

[9]W.Bergweiler,X.C.Pang.On the derivative of meromorphic functions with multiple zero.

[9]W.Bergweiler,X.C.Pang.On the derivative of meromorphic functions with multiple zeros[J].J.Math.Anal.Appl.,2003,278(2)：285-292.

[10]Y.Xu.On the value distribution ofderivatives of meromorphic functions[J].Appl.Math.Lett.,2005,18(5)：597-602.

[11]Y.Xu.Picard values and derivatives of meromorphic functions[J].Kodai Math.J.,2005,28(1)99-105.

[12]X.C.Pang,M.L.Fang,L.Zalcman.Noraml families of holomorphic function with multiple zeros[J].Conf Geom Dyn,2007,11：101-106.

[13]X.J.Huang,Z.X.Liu.A Normal criterion concerning shared Values[J].Acta Math Scientia.2011,31：540–545.

（责任编辑：陈 辉）

A Teaching Note on Picard Theorem

LIU Zhi-xiu
(Science Department of Nanchang Institute of Engineering,Nanchang,Jiangxi,330099)

Generally,the introduction or even proof on Picard's celebrated theorem is included in the complex function teaching process.But if the teacher does not explicitly point out the equivalence of Picard big theorem and small theorem,students may easily produce wrong guess that the small theorem does not contain the big theorem.This is not conducive to the students’understanding of the Picard theorem as well as the development of the subject.Actually,they are the same equivalence effective theorem.The purpose of this paper is to emphasize this point of view and use the Zalcman-Pang lemma of normal family theory to prove the equivalence of Picard theorems.

Picard theorem;Meromorphic function;normal family;mold distribution

G642

A

123（2014）02-0045-03

2013-10-15

刘芝秀（1982-），女，四川自贡人，南昌工程学院，硕士，讲师。研究方向：复分析及其应用。

易 敏（1963-），男，江西余江人，南昌工程学院，副教授。研究方向：应用数学。