各国桥梁规范中温度梯度模式作用下混凝土箱梁桥温度效应对比分析

戴 婷，李和志，刘方华，李曼曼，陈 辉

（江西科技学院 土木工程学院，江西 南昌 330098）

各国桥梁规范中温度梯度模式作用下混凝土箱梁桥温度效应对比分析

戴 婷，李和志，刘方华，李曼曼，陈 辉

（江西科技学院 土木工程学院，江西 南昌 330098）

通过收集并整理国内外桥梁设计规范中几种典型的沿箱梁截面竖向温度梯度模式，对各梯度模式采用相同的温度基数，借助有限元软件建立模型对这些温度梯度产生的温度效应进行比较。分析结果表明：根据现行公路规范(JTG D60-2004)计算得到的温度拉应力偏小，温度梯度产生的横向应力与纵向温度应力处于同一数量级，且横向温度拉应力大于纵向温度拉应力值。

温度梯度；有限元模型；混凝土箱梁桥；温度效应

0 引言

随着预应力技术和悬臂施工方法的成熟发展，预应力混凝土箱梁结构广泛应用于公路桥梁的建设。箱梁结构具有良好的受力特性，其截面形式便于预应力筋的配置，能够抵抗正负弯矩，有很强的适用能力。在预应力混凝土箱梁桥修建及其向轻型、大跨、薄壁发展的过程中，出现了许多工程问题。据调查，大量预应力混凝土箱梁桥在施工阶段和运营过程中出现裂缝，引起裂缝的重要原因之一是温差作用[1-2]。如漓江二桥、九江长江大桥引桥、新响琴大桥等，都因温度的作用导致桥梁裂缝的形成甚至破坏[3-5]。温度应力引起的桥梁裂损甚至破坏给工程建设带来了不可忽略的经济损失。因此，有必要从温度荷载和结构优化等方面进行研究，以保证桥梁结构的安全性、耐久性要求，降低在设计使用年限内的维修费用。虽然已有专家在此方面进行了大量研究，但一直未达成共识。中国现行公路规范(JTG D60-2004)中温度梯度模式是参照美国规范确定的[6-7]。本文通过对比各国规范中梯度模式在同一箱梁结构上的温度效应，探讨公路桥涵设计规范(JTG D60-2004)的不足之处，以便为新规范的制定提供参考依据。

1 各国温度梯度模式

虽然一些国家的桥梁设计规范仍采用线性温度梯度曲线，但是研究表明沿混凝土箱梁高度方向，温度是非线性分布的。因此，在参考各国规范之后，选取以中国铁路规范为代表的指数曲线梯度模式、以新西兰规范为代表的五次幂函数梯度模式以及以美国、英国、中国公路规范为代表的折线形梯度模式为代表进行研究。

1.1 中国铁路规范

现行铁路桥涵设计规范（TB 10002.3-2005）规定混凝土箱梁桥应考虑沿截面温差引起的纵向和横向温度应力，对日照温差荷载的规定如下：有渣箱梁只考虑沿梁宽方向的温度荷载，无渣无枕箱梁则应分别考虑沿梁高方向的温差荷载和两个方向的组合温差荷载[8]。

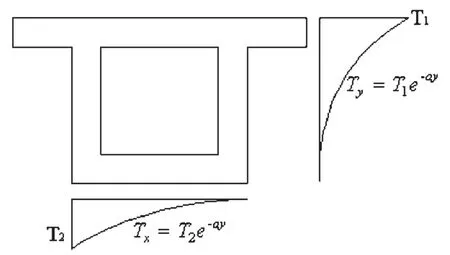
图1 中国铁路规范日照温度梯度

表1 日照温度梯度的a值和T值

1.2 新西兰规范

新西兰公路桥梁设计规范[9]规定的竖向温度梯度模式为从梁顶沿梁高向下1200mm范围内降至0的五次幂函数曲线，并在梁底200mm内存在1.5℃的反向温差,如图2所示。

1.3 中国公路规范

中国公路桥涵设计通用规范（JTG D60-2004）给出如图3所示的竖向温度梯度曲线，桥面板表面的最高温度T1规定见表2。对梁高H小于400mm的混凝土结构，图3中A为H-100（mm）；对于梁高H等于或大于400mm的混凝土结构，A=300mm。

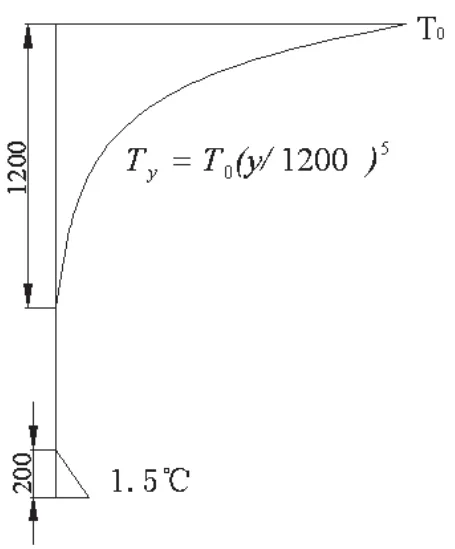
图2 新西兰规范竖向温度梯度

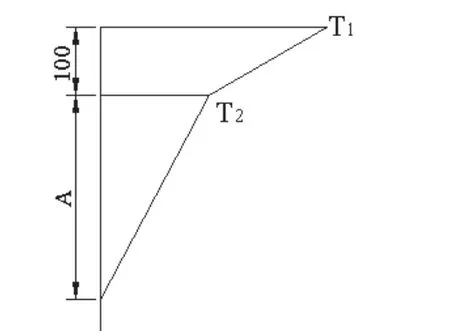
图3 中国公路规范竖向温度梯度

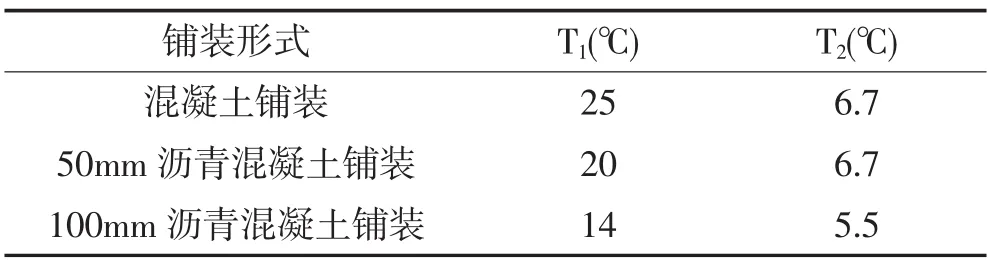
表2 竖向日照温度梯度的温度基数

1.4 计算温度梯度模式

各规范中提供的温度梯度曲线采用不同的温度基数，为使对比结果更能体现温度梯度线形对温度效应的影响，本文中各温度梯度曲线采用相同的温度基数20℃，即得到温度梯度Ⅰ（参照中国公路规范）：T1=20，T2=6.7；温度梯度Ⅱ（参照中国铁路规范）：T=20e-5y；温度梯度Ⅲ（参照新西兰规范）：T=20(y/1.2)5，各梯度曲线如图4所式。

图4 不同竖向温度梯度比较

2 有限元分析

2.1 基本理论和方程

平衡微分方程

取权函数为真实位移的变分δui，边界值取负值。δui连续可导，且在给定位移的边界上δui=0，因此可以得到以上三式的等效积分形式为

N为形函数矩阵，B为应变矩阵，a为节点位移矩阵，L为微分算子，D为弹性矩阵

由式（6）可得到最小位能原理，其泛函表达式为

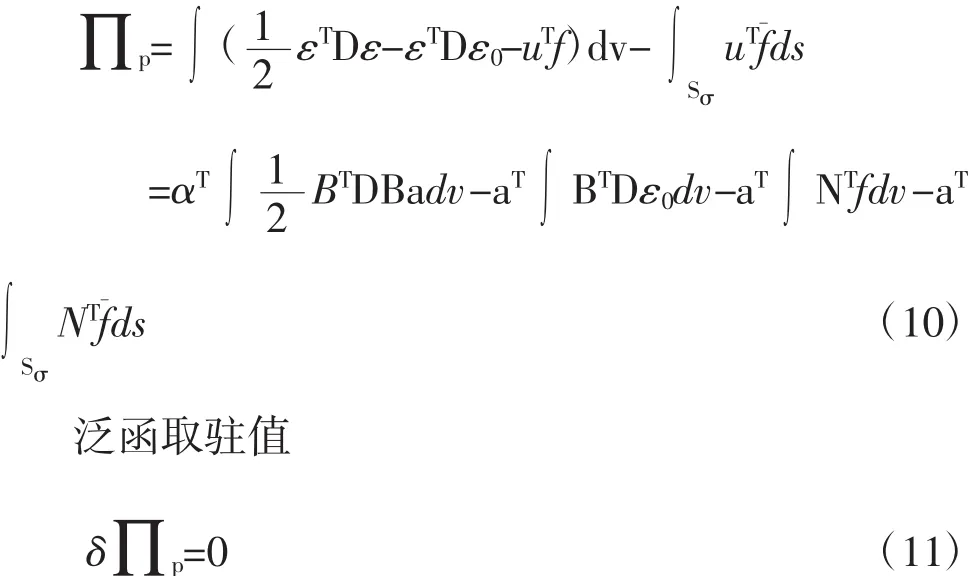
将求解域V进行有限元离散，即得到有限元的求解方程

其中，K为结构的刚度矩阵，P为结构上的节点荷载矩阵

2.2 有限元分析模型

本文借助通用有限元分析软件ANSYS，并以湖南某45m+70m+45m三跨预应力混凝土连续刚构桥为原型建立有限元模型，其结构总体布置如图5所示，在两端支座及跨中位置梁高2.8m，中间两处桥墩位置梁高4.5m，其间梁高按二次抛物线变化。单箱顶板宽18.5m，悬臂长度为4.5m，底板宽9.5m。箱梁具体尺寸参见图6。

图5 湘江特大桥引桥结构布置图

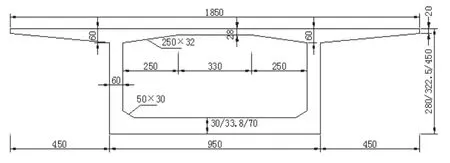
图6 箱梁截面尺寸图

选取结构分析单元SOLID45，该类型单元有8个节点。对整个结构采用映射划分网格，单元尺寸为0.5m，并对顶板温度变化较大的位置进行加密划分，如图7所示。在梁两端支座位置处对x和y向的位移约束，在跨中两桥墩处对各向的位移约束，并在沿桥梁纵向的各截面上施加相同的温度荷载。

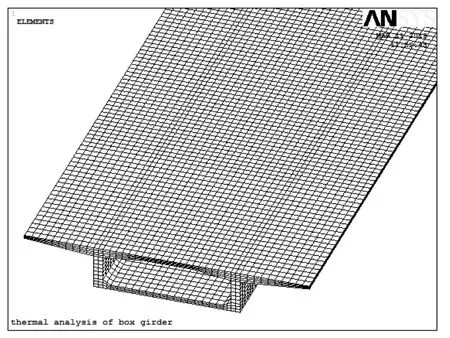
图7 空间模型局部

3 计算结果分析

根据图4所示的竖向温度梯度曲线，利用前述的空间有限元模型，计算混凝土箱梁在图8各截面位置的纵向及横向温度应力，其结果分别如表3、表4所示。

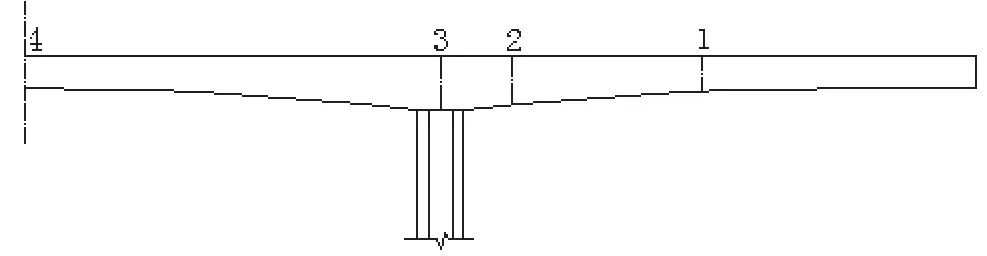
图8 截面位置

纵向最大压应力出现在截面4，即中跨跨中截面的顶板外表面，其中按梯度Ⅱ计算得到的值最小，为6.6Mpa。按梯度Ⅰ计算得到的值最大，为7.01Mpa，最大值与最小值之间相差0.39Mpa。纵向最大拉应力出现在截面2的底板内表面。按梯度Ⅲ计算得到的值最大，为2.56Mpa，与按梯度Ⅱ计算的结果非常接近。按梯度Ⅰ计算得到的值最小，为1.73Mpa，最大值与最小值之间相差0.83Mpa。

各截面顶板内外表面的横向温度应力变化非常小，最大差距仅为0.06Mpa。取横向温度应力最大的截面2进行对比，按梯度Ⅰ的压应力最大，为5.94Mpa，按梯度Ⅲ计算的压应力最小，为4.55Mpa，相差为1.39Mpa。拉应力的情况则相反，按梯度Ⅲ计算得到的拉应力最大，为3.17Mpa，按梯度Ⅰ计算得到的拉应力最小，为2.67Mpa，相差为0.43Mpa。而公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62-2012)[10]中只给出了纵向温度应力的计算方法，这显然是不充分的。

表3 纵向应力（单位：Mpa）

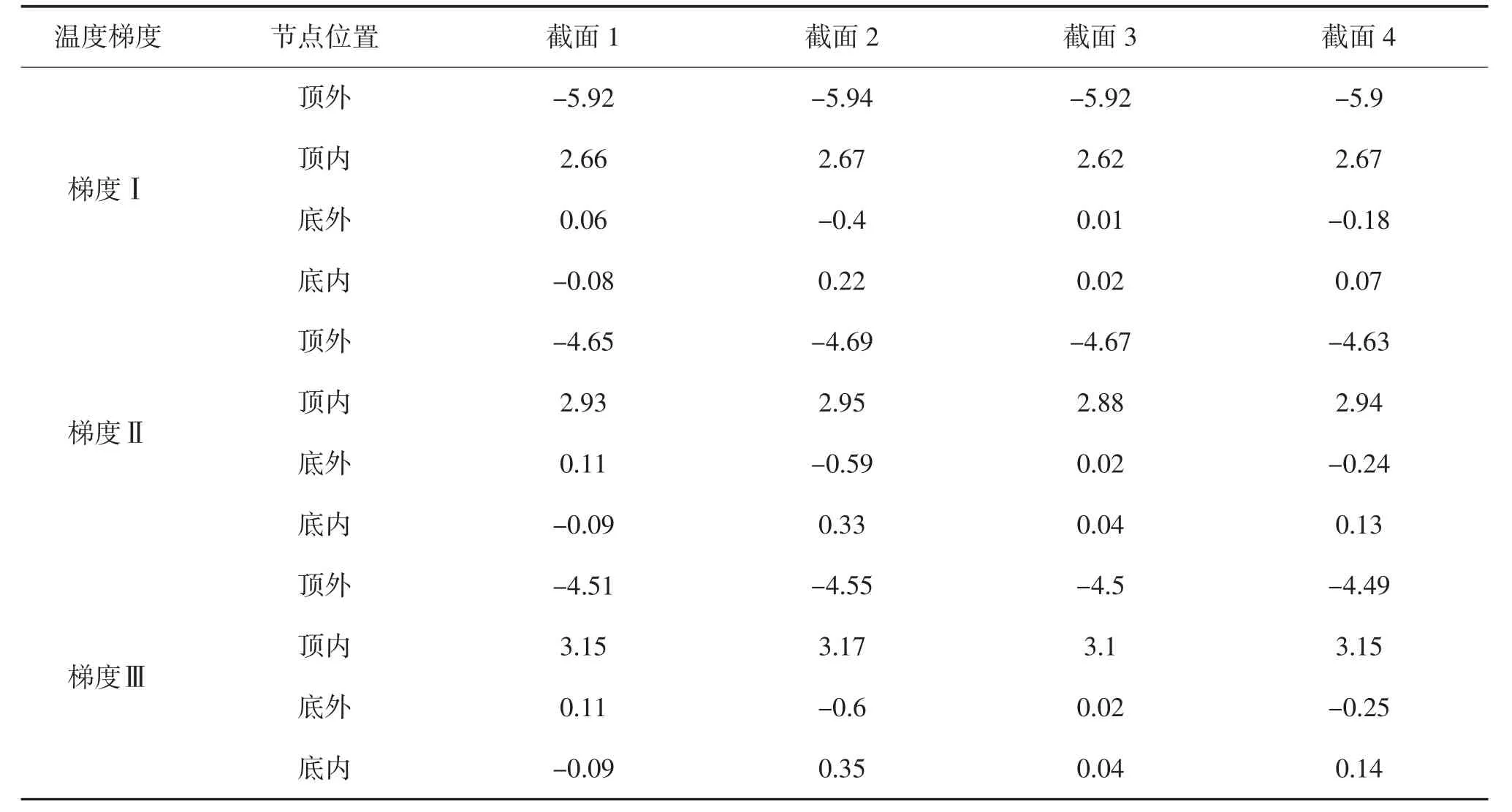
表4 横向应力（单位：Mpa）

计算结果表明由公路桥涵设计通用规范(JTG D60-2004)规定温度梯度形式得到的温度拉应力值最小，而温度裂缝的产生是因为温度拉应力超过了混凝土的抗拉强度。竖向温度梯度引起的纵横向温度应力值为同一个数量级，且横向温度拉应力大于纵向温度拉应力值，表明公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62-2004)中只给出纵向温度应力的计算公式是不充分的。

[1]朱汉华，陈孟冲，袁迎捷.预应力混凝土连续箱梁桥裂缝分析与防治[M].北京：人民交通出版社，2006.

[2]Li DN，Maes MA.Dilger WH.Evaluation of temperature data of Confederation Bridge：Thermal loading and movement at expansion joint [J].Proceedings of the ASCE：Structure Congress，2008，120(1)：314-324.

[3]刘兴法.混凝土结构的温度应力分析[M].北京：人民交通出版社，1991.

[4]彭友松，陈钒，刘悦臣.株六复线新响琴峡大桥温度效应分析[J].中国铁道科学，2008，29（6）：46-49.

[5]何伯雷.“太阳把桥晒跑了？”——深圳市某立交A匝道桥事故分析[J].城市道桥与防洪，2002，2：39-43.

[6]公路桥涵设计通用规范（JTG D60-2004）[S].北京：人民交通出版社，2004.

[7]美国各州公路和运输工作者协会（AASHTO），辛济平，万国朝，张文等译.美国公路桥梁设计规范-荷载与抗力系数设计法（SI单位，第一版，1994年）[M].北京：人民交通出版社，1998.

[8]铁路桥涵钢筋混凝土和预应力混凝土结构设计规范（TB 10002.3-2005）[S].北京：中国铁道出版社，2005.

[9]彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都：西南交通大学，2007.

[10]公路钢筋混凝土及预应力混凝土桥涵设计规范（JTG D62-2012）[S].北京：中国人民共和国交通运输部发布，2012.

（责任编辑：陈 辉）

Comparative Analysis of Temperature Effect on Concrete Box-girder Bridge under Action of Different Thermal Gradients in Bridge Design Codes of Different Countries

DAI Ting,LI He-zhi,LIU Fang-hua,LI Man-man,CHEN Hui
(Civil Engineering School,Jiangxi University of Technology,Nanchang,Jiangxi,330098)

The paper collects and sorts vertical thermal gradients at cross sections of concrete box girder bridges in bridge design codes of different countries.Adopting the same basic temperature data to respective gradient mode,with the help of universal finite element software,a comparison is made towards the temperature effects resulted from these thermal gradients.The results show that tensile temperature stress,due to thermal gradient in General Code for Design of Highway Bridges and Culverts,is comparatively small.Transverse stress and longitudinal stress,due to thermal gradient,is of the same order of magnitude,and transverse stress is larger than longitudinal stress.

thermal gradient;finite element model;concrete box-girder bridge;temperature effect

U446

A

123（2014）02-0037-05

2013-08-11

戴 婷（1989-），女，湖南娄底人，江西科技学院土木工程学院，硕士。研究方向：混凝土箱梁结构温度效应。