基于影响系数矩阵的某型发动机稳态模型修正

马 力，杨天南，薛庆增

(中国人民解放军海军驻沈阳地区发动机专业 军事代表室，沈阳 110043)

基于影响系数矩阵的某型发动机稳态模型修正

马 力，杨天南，薛庆增

(中国人民解放军海军驻沈阳地区发动机专业 军事代表室，沈阳 110043)

引入影响系数矩阵的方法，修正发动机稳态模型，使修正后的模型能更好地与实际发动机相符合。仿真结果表明，模型修正后精度有很大提高，并且利用影响系数矩阵方法迭代修正的模型精度优于一次修正的结果。进一步指出模型修正精度与所选的待修正部件参数与目标性能参数的敏感性密切相关。

模型修正；影响系数矩阵；敏感性

发动机由于制造、安装工艺等的不同，其部件特性有差异，并且在使用过程中存在性能退化，使得每台发动机的特性也会不完全相同[1-2]。热力学建模技术和一些发动机性能仿真计算软件已经能够越来越准确的建立发动机稳态模型。但是，这些技术仍然难以在没有足够发动机部件特性数据(例如空气流量、压比、效率等)的情况下建立准确的发动机模型，得到的结果与实际值可能存在较大的偏差[3]。发动机测量参数的准确性对分析单台发动机性能变化有着重要影响。准确的发动机稳态模型是开展性能评估和预测的前提和基础。因此，发动机稳态模型修正显得十分必要。

Stamatis等人介绍了修正系数法(MF,Modification Factors)，并用广义最小残差法修正系数[4]。文献[5]采用部件法建立了某型涡扇发动机的基准数学模型，首先采用小波分析实现对测量数据的预处理，通过建立状态空间修正模型，比较了模型修正前后的精度。文献[6]以阶跃输入响应进行模型检验，提出了状态空间模型的修正方法。文献[7]以Kalman技术修正测量参数偏离量，提高了模型精度。

利用迭代修正影响系数的方法，对发动机稳态模型进行修正，使之能更好的符合发动机实际使用情况。讨论并分析了待修正部件参数对目标性能参数的敏感性对模型修正精度的影响。

1 基于影响系数矩阵的模型修正

发动机在设计点的稳态模型修正是一个反向的数学问题。文献[8]在发动机气路故障诊断方法中应用了影响系数矩阵(ICM,Influence Coefficient Matrix)的逆矩阵模型，有效解决了发动机模型的自适应修正。值得注意的是，在整个发动机模型自适应修正过程中，有两类参数需要事先定义：

(1)待修正的部件参数—也称为发动机设计点部件参数(自变量)。例如空气流量Wα22、高压压气机增压比πcH、高压压气机效率ηcH、高压涡轮效率ηTH等。

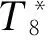
利用影响系数矩阵方法，在设计状态对发动机稳态模型进行修正，影响系数矩阵方法分为一次修正模型和多次修正模型。

1.1 一次修正模型

发动机待修正的部件参数与目标性能参数之间的热力关系可以表征为

z=h(x)

(1)

式(1)中，目标性能参数向量z∈RM，M是目标性能参数的个数；待修正的部件参数向量x∈RN，N是待修正的部件参数的个数；h(x)是多目标判别函数。基准点用下标0表示，则式(1)在基准点按Taylor级数展开，即

(2)

式(2)中，H.O.T为高阶小量，其影响不大，可以忽略。因此基准点的待修正部件参数的偏离量和目标性能参数的偏离量之间的关系式线性化表示为

Δz=H·Δx

(3)

可以选择这些待修正的部件参数设计点作为初值，与之相对应的目标性能参数与实际值相比可能会存在一定的误差。通过对影响系数矩阵H求逆，得到自适应系数矩阵H-1，就可以用相对应基准点的目标性能参数的误差来估计待修正部件参数的偏差。当时N=M，

Δx=H-1·Δz

(4)

一般情况下，待修正的部件参数N和目标性能参数M并不相等。此时，可以得到待修正部件参数最小二乘解。

Δx=H#·Δz

(5)

其中

(6)

在待修正的部件参数与初始值的偏差不是很大，并且发动机稳态模型在设计点为近似线性的情况下，发动机部件参数从初始值变化到合适的数值时，Δx的线性估计值将是这个偏差良好的估计，其计算流程如图所示。

图1 一次修正模型修正流程图

1.2 迭代修正模型

如果待修正的部件参数和目标性能参数之间关系是强非线性的，用1.1节的一次修正模型得到的目标性能参数与实际值相比仍会有较大误差。为了改进修正模型的精度，可以通过Newton-Raphson算法进行反复迭代来建立修正稳态模型，收敛过程如图所示。

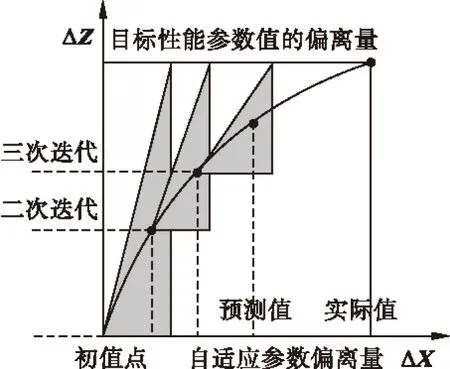
图2 迭代修正模型的修正过程收敛图

当预测值十分接近实际值的时候，图2的迭代收敛过程停止迭代。当迭代一次或者单次迭代收敛时，即为上述的一次修正模型。收敛准则为预测参数和实际参数的标准差RMS小于事先给定的阀值δ。

(7)

其中，选取δ=0.001。

每一个目标性能参数计算误差可以用模型的估计值和发动机实际参数值来表示。

(8)

修正模型中选择低压压气机出口空气流量Wa22、低压压气机压比πcL、高压压气机效率ηcH、低压涡轮效率ηTL、低压涡轮流量Wst5和高压涡轮流量Wst45等6个参数作为待修正的部件参数；选择低压压气机出口温度T2、低压压气机出口压力P2、高压压气机出口温度T3、高压压气机出口压力P3、低压涡轮出口温度T5等5个参数作为目标性能参数。

1.3 迭代修正模型的Newton-Raphson解法

对于多元非线性方程组Z=F(X)，已知第k次试取值：

(9)

残差

(10)

求第k+1次试取值Xk+1，力求使Z(k+1)=0。

使用N-R法，则有：

ΔZ=H·ΔX

(11)

其中，

(12)

(13)

迭代的目标是求出使Z(k+1)=0的第(k+1)次试给值X(k+1)，对于多元方程ΔZ=H·ΔX，若要使Z(k+1)=0，则应取：

ΔZ=Z(k+1)-Z(k)=-Z(k)

(14)

将此式代入到ΔZ=H·ΔX，可得：

H·ΔX=-Z(k)

(15)

对该方程组求解，可得：

ΔX=H-1(-Z(k))

(16)

试取新值

X(k+1)=X(k)+ΔX

(17)

以新的试取值重新进行计算，一直到RMS<δ。

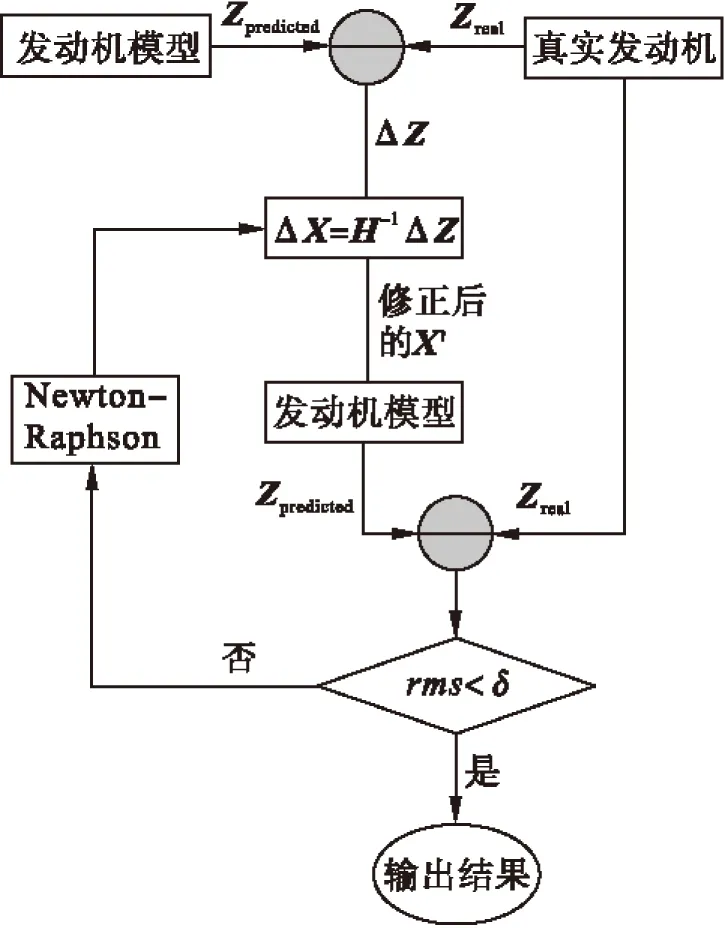
图3 迭代修正模型的流程

2 影响系数修正模型的求解与分析

(18)

用同样的方法可依次求得对其他性能参数xi(i=2,3,…,M)的近似偏导数，这样可以得到整个系数矩阵H的所有元素值，进一步得到发动机设计点的影响系数矩阵数值，结果见表1。

选择发动机工作状态稳定在设计状态附近时作为测量点，考虑到生产、制造公差等原因，本文认为设计状态附近的测量点即为发动机的设计点，并多次测量取平均值即为最后的测量值。如果测量点选择不是在海平面标准条件，要对其推力等性能参数进行修正。

理论上，非线性修正模型因为考虑了发动机模型的强非线性关系，所以其修正的结果要比线性模型更加接近于真实值；但是非线性修正模型需要更多次的迭代与更复杂的非线性运算，因此运行的时间会更长。基于迭代修正的影响系数方法在一定程度上满足了模型修正的精度，如果修正的模型精度达不到预期目标，可采用多次迭代修正的方法，以提高模型修正精度。在影响系数修正中，设置6个待修正部件参数，分别利用一次修正模型和迭代修正模型对5个相同目标性能参数进行修正，修正结果见表2和表3。

表1 设计点的影响系数矩阵元素值

表2 一次修正模型与迭代修正模型的结果比较

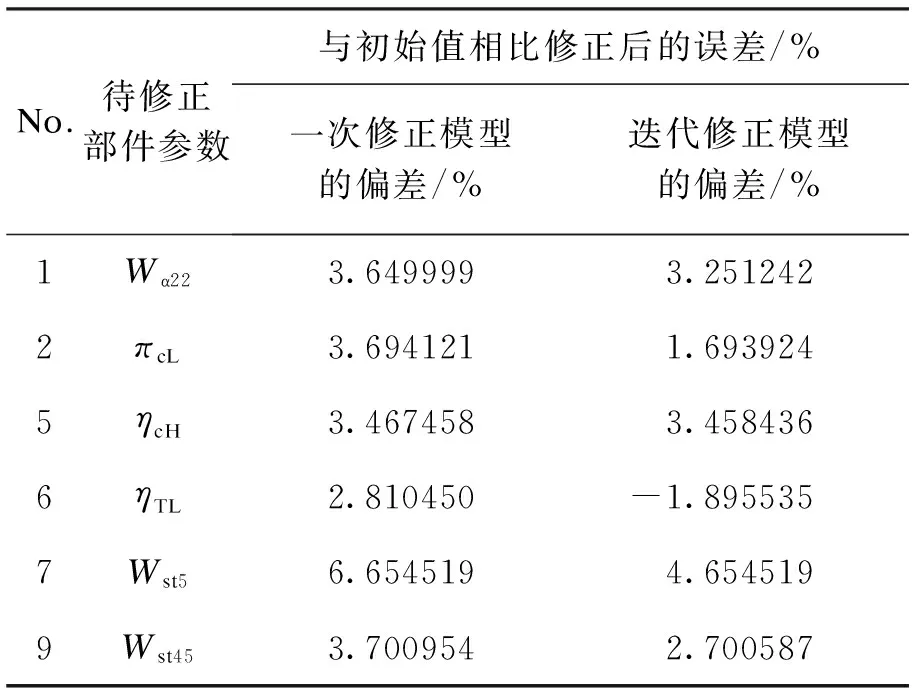
表3 一次修正模型与迭代修正模型的待修正参数偏差

表2给出了发动机稳态模型未修正、一次迭代修正、多次迭代修正后的精度。

表3同时对比了分别经过一次修正模型和迭代修正模型修正后的待修正部件参数的偏差量，多次修正后的部件参数偏差与一次修正后的偏差并无明显的关联。进一步从表1中可以看出迭代修正模型的精度要明显好于一次修正模型的精度。由计算可以得到，经过约40次的迭代达到收敛指标限制。因此迭代修正模型将首选作为基于影响系数矩阵的修正模型。

在上述基于影响系数矩阵修正模型中，选择了6个待修正的部件参数，5个目标性能参数。但是改变待修正部件参数的个数，修正结果会有所差别，结果见表4和表5。仍然选择全部5个目标性能参数，但只选5个待修正的部件参数(未选Wst45)。从表4和表5中可以看出，目标性能参数与初始值的偏差变化并不明显，但是待修正部件参数的偏差有比较明显的差别。

表4 两种组合的待修正参数偏差量对比

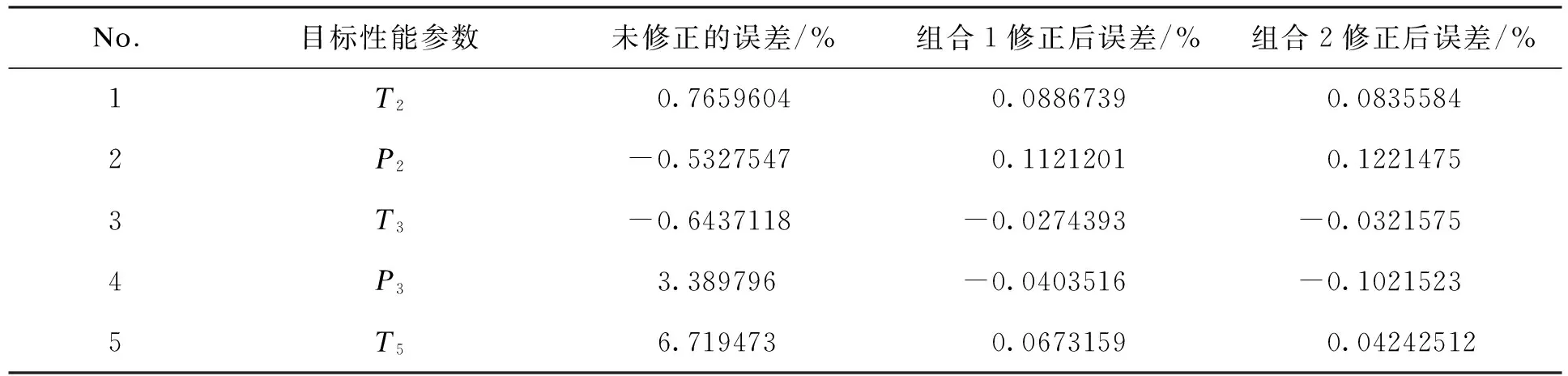
表5 两种组合的迭代模型修正结果比较

保持其他待修正部件参数不变，每次仅改变一个待修正部件参数值，使其增大1%，基于发动机稳态模型，对所有待修正参数进行目标参数敏感性分析。选择不同待修正部件参数组合对自适应修正效果有明显影响。通过计算发现，不包括或者的待修正参数组合对应的修正精度没有明显的变化，这两个部件参数对发动机性能参数的影响敏感性不强；而没有选择敏感性强的待修正部件参数的修正模型，可能会导致代修正部件参数估计结果的发散。

因此在基于影响系数矩阵的修正模型中，待修正部件参数必须要将敏感性强的部件参数包括进来，如果漏选这些参数，那么修正模型很难得到正确的结果，迭代结果也可能趋于发散。

3 结 语

实际应用中发动机由于生产、制造工艺等原因，即使是同一批次生产的发动机，每台发动机的特性也不尽相同，同时使用过程中性能出现衰退。因此对所建立的发动机稳态模型进行修正。采用迭代修正影响系数矩阵的方法对发动机模型进行修正，取得了不错的效果。在模型修正过程中，尽量选取敏感性强的待修正部件参数，才能保证模型修正过程不致发散，修正结果精度高。

[1]谢小平.某型发动机气路模型修正研究[D].烟台:海军航空工程学院,2011:23-25.

[2]李冬,王冠超,曹明川.基于遗传算法的发动机气路性能模型修正研究[J].燃气涡轮试验与研究，2012:25(4):46-50.

[3]翟高兰.航空发动机非线性参数估计方法[D].南京:南京航空航天大学,2008：45-46.

[4]Stamatis A,Mathioudakis K,Papailiou K D.Adaptive simulation of gas turbine performance[J].Gas Turbine Power,1990,112(2):168-175.

[5]李本威,尹大伟,樊照远,等.某型涡扇发动机状态模型修正[J].海军航空工程学院学报,2008,23(2):213-216.

[6]郑铁军.建立航空发动机状态空间模型的修正方法[J].推进技术，2005,26(1):923-926.

[7]王永华,孙涛,王秀霞.基于Kalman滤波的航空发动机模型研究[J].燃气轮机技术，2011,24(1):31-34,39.

[8]Escher P C,Singh R.An objective-oriented diagnostics computer program suitable for industrial gas turbine[C].21st International Congress on Combustion Engines(CIMAC).Switzerland,1995:15-18.

(责任编辑：宋丽萍 英文审校：宋晓英)

Themodificationofstablestatusenginemodelbasedoninfluencecoefficientmatrix

MA Li,YANG Tian-nan,XUE Qing-zeng

PLA Navy Engine Professional Military Representative Office in Shenyang Area,Shenyang 110043,China)

Aiming at solving this problem,influence coefficient matrix was introduced and stable status model was modified,so that the model modified can correspond to factual engine.Simulated result indicates that the precision of modified model is enhanced greatly,and the precision of the model iteratively modified by influence coefficient matrix is superior to that after one single modification.And it is shown that precision of modified model correlates to the sensitivity of selected component parameter to the objective performance parameter.

modification of model;influence coefficient matrix;sensitivity

2013-12-16

马力(1977-)，男，辽宁沈阳人，工程师，主要研究方向：传动与润滑，E-mail:：2369887145@qq.com。

2095-1248(2014)02-0032-05

TE626.3

A

10.3969/j.issn.2095-1248.2014.02.008