基于GJK的凸体快速连续碰撞检测研究

刘 丽，张国山，邴志刚，刘 敏

(1.天津大学电气与自动化工程学院，天津 300072；2.天津信息感知与智能控制重点实验室，天津 300222)

基于GJK的凸体快速连续碰撞检测研究

刘 丽1，张国山1，邴志刚2，刘 敏1

(1.天津大学电气与自动化工程学院，天津 300072；2.天津信息感知与智能控制重点实验室，天津 300222)

针对一段时间内的多个运动物体之间的碰撞检测，提出一种基于距离算法(Gilbert-Johnson-Keerthialgorithm，GJK算法)的凸体快速连续碰撞检测算法，该算法主要通过判断一段时间内两物体之间的最小距离是否为零来检测碰撞发生情况。首先利用GJK算法在有限步骤内计算得到最小距离，检测两物体是否发生碰撞；若两物体发生碰撞，进而利用ray-casting算法确定发生碰撞的精确位置，根据环境要求做出相应响应，调整运动物体位置。仿真结果表明，对多个运动物体间的连续碰撞检测，该算法有较高的实时性和准确性。

连续碰撞；GJK算法；运动物体；碰撞检测；凸体

碰撞检测在计算机图形学、CAD/CAM、虚拟现实、虚拟制造、三维游戏等诸多领域都有广泛的应用，是提高虚拟场景物理真实感的关键问题之一[1-4]。按照场景模式不同，碰撞检测主要分为静态检测和动态检测。动态检测针对场景中至少存在一个运动物体的情况；根据碰撞检测方式的不同，动态检测分为离散检测和连续检测[5]。离散碰撞检测算法是对运动物体进行取样检测，因此容易造成漏检测，进而产生穿透现象[6]。针对两物体间的穿透现象，连续碰撞检测算法通过对一段连续时间内物体的运动过程进行建模，判断两物体之间的碰撞情况，可以很好地解决漏检测问题[6]，但计算量相对较大。目前，虚拟环境的场景复杂度越来越高，对碰撞检测的实时性及准确性的要求也越来越高。因此，提高检测实时性及准确性是连续碰撞检测要解决的关键问题。

经过多年发展，目前已有多种连续碰撞检测算法，主要有基于扫描实体的算法[7-8]，应用Minkowski和与球面高斯映射相结合的方法[9]，保守前进算法及其改进算法[10]，基于GJK的算法[11-13]以及张应中等提出的线性连续碰撞检测(linear continuous collision detection，LCCD)算法[13]等。其中，基于扫描实体的方法及应用Minkowski和与球面高斯映射相结合的方法计算量都较大，不适合实时碰撞检测；基于CA及其改进算法虽然提高了检测精度和速度，但其本质仍属于基于步长的碰撞检测；LCCD算法适用于简单凸体之间的碰撞检测。

为提高碰撞检测的快速性及精确度，针对多个凸体之间的连续碰撞检测，本文提出一种基于GJK的快速连续碰撞检测(fast continuous collision detection，FCCD)算法。该算法以Minkowski差集为工具，可在有限步骤内计算得到两物体间的最小距离，检测两物体是否发生碰撞，加快碰撞检测速度，并利用ray-casting算法计算得到凸体间第一次发生碰撞的位置，及时作出碰撞响应。最后通过仿真对本文算法和LCCD算法进行了比较，仿真结果表明该算法具有较高的实时性和准确性。

1 GJK算法概述

GJK算法是本文算法的基础，下面对GJK算法涉及到的相关几何理论、概念以及GJK算法的基本理论进行介绍。

1.1相关定义

定义1：d-单形体是指d维空间内，仿射无关的点集形成的凸包。如0是单形体是指一个点；1是单形体是指一条线段；2是单形体是指一个三角形；3是单形体是指一个四面体[14]。

图1 凸体C在方向d上的支撑点PFig.1 Support point P of convex C in direction d

定义2：对于凸体集C，沿给定方向且距离该集合最远的一点称作C的支撑点。如果对于给定的方向d，有d·P=max{d·V:V∈C}，则P称为C的支撑点，即点P使得d·P存在最大值。图1为2个不同凸体集在方向d上的支撑点[14]。

定义3：支撑映射(又称为支撑函数)是一个函数，其关联一个凸体集C，将方向映射d至C的支撑点，记为Sc(d)。对于球体、盒体、圆柱体、椎体等简单的凸体，支撑映射以闭合方式加以限定。例如，对于球心为O、半径为r的球体，其支撑映射的定义为Sc(d)=O+rd/‖d‖，对应的支撑点如图1b)所示。

对于复杂度较高的凸体，其支撑映射函数要利用相应的数值方法如爬山法等确定支撑点[14]。

定义4：在实数向量空间中，凸包(convex hull)就是包含一个几何对象的最小(最紧凑)包围体[14]。对于三维空间中的一个给定点集X，包含X的所有凸集的交集就是X的凸包，记为CH(X)。

定义5：A和B为2个点集，且令a和b为2个位置向量，对应A和B中的顶点。则A和B的Minkowski差为A⊖B={a-b:a∈A,b∈B}[14]。

定义6：配置空间障碍(configuration space obstacle，CSO)是2个凸体的Minkowski差集所构造的凸包[14]。

Minkowski差在两物体间的碰撞检测中起着十分重要的作用：当且仅当A和B的Minkowski差C(C=A⊖B)包含原点时，A和B发生碰撞[14]。

1.2算法基本原理

GJK算法是由Gilbert，Johnson和Keerthi 3人在1988年共同开发的一类迭代算法[11-12]。GJK算法的输入为两物体的顶点集，通过有限次数的迭代后，最后输出结果为两物体之间的欧氏距离。根据两物体之间的欧氏距离，可进行碰撞检测。当两物体之间的距离等于或者小于零时，可判定两物体发生碰撞。

假设两凸体A和B，两凸体之间的距离为d(A,B)，则d(A,B)可用式(1)来表示：

d(A,B)=min{‖x-y‖:x∈A,y∈B}。

(1)

GJK算法还可以返回2个物体之间距离最近的2点a和b，满足：

‖a-b‖=d(A,B),a∈A,b∈B。

(2)

如果定义v(C)为凸体集C中离原点最近的一个点，满足：

v(C)∈C且‖v(C)‖=min{‖x‖:x∈C}。

(3)

则A和B之间的距离可用Minkowski差表示为

d(A,B)=v(C)，

(4)

式中，C=A⊖B。

通过上面的变化，该算法可等效为计算两凸体A和B的Minkowski差C(C=A⊖B)构成的凸包与原点之间的距离，即求解2个凸体的CSO上距原点的最近点，这样可大大简化计算，如图2所示。

图2 距离等价图Fig.2 Distance equivalent

GJK算法通过在CSO边界上降序迭代求得CSO中距离原点最近的点。在每次迭代过程中，在CSO中生成一个单形体，并且确保其所含顶点比上一次迭代中产生的单形体更接近于原点。定义Wk是在第k次迭代过程中生成的单形体，始终包含1到4个顶点；vk是这个单形体中距离原点最近的点，通过“距离子算法”(或Johnson算法)计算得到vk[14]。对于凸体对象，GJK算法可通过有限步的迭代运算返回最终结果。GJK算法的迭代过程如下。

初始条件时，W0=∅,v0为CSO中任意点。

1) 初始化单形体Wk为CSO中一个或多个顶点(最多为4个)。

2) 通过距离子算法计算得到vk。

3) 若vk为原点，则原点就在CSO中，A，B两物体发生碰撞。GJK算法结束并返回“A，B相交”。

4) 针对Wk中不包含顶点vk的子单形体，将其顶点从单形体中移除。

5) 令wk=SA-B(-vk)为-vk方向上的支撑点。

6) 与顶点vk比较，若点wk在-vk方向上并非极值点，即‖vk‖2+SA-B(-vk)·(-vk)=0，则结束迭代过程，并返回“A和B不相交”。由原点指向顶点vk的向量长度‖vk‖即为A和B之间的距离。

7) 否则，将wk添加至单形体Wk中并返回步骤2)。

2 快速连续碰撞检测算法

本文以GJK算法为基础，通过判断一段时间内2个凸体间判断一段时间内两物体之间的最小距离是否为零来检测是否发生碰撞。如果两物体发生碰撞，则通过射线与凸体相交的方法得到碰撞发生的位置，根据环境要求做出响应。本文算法分为2步进行，第1步为碰撞检测，快速检测碰撞是否发生；第2步为碰撞响应，计算碰撞发生的位置。

2.1检测碰撞

文献[15]与文献[16]提出了应用GJK算法实时计算二维平面中2个线性运动物体之间的最小距离。本文对其算法进行推广，应用到检测三维空间中两凸体之间是否发生碰撞。

1)问题描述 本算法应用于有多个运动物体的场景，需要对场景中的物体进行两两检测。为不失一般性，假设场景中的2个运动物体分别为A和B，在时间区间[t0,t1]内，A和B均做匀速直线运动，其速度为常量，分别为vA和vB。

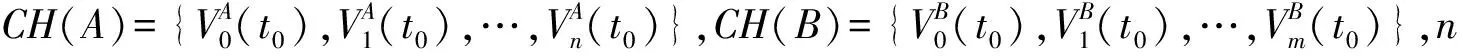
在时间区间[t0,t1]内，CH(A)，CH(B)的位置顶点可如式(5)和式(6)表示：

(5)

(6)

式中，Δt=t1-t0，t=t0+α·Δt:∀t∈[t0,t1]，α∈[0,1]，i∈{1,2,…,n}，j∈{1,2,…,m}。

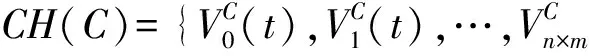
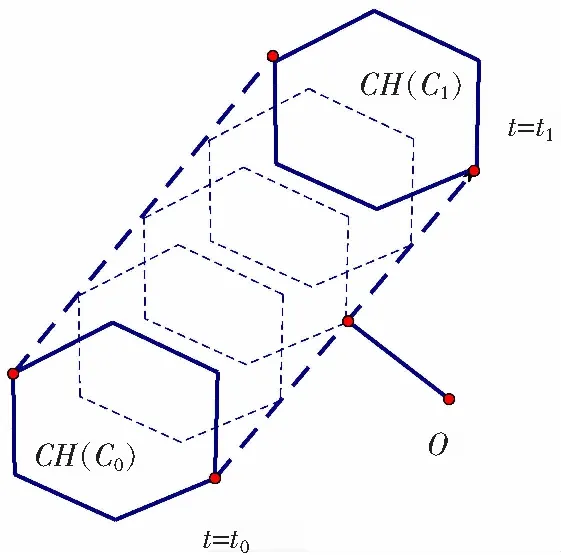
图3 CSO在时间[t0,t1]内的运动轨迹Fig.3 CSO trajectory in [t0,t1]

(7)

由式(7)可知，在时间区间[t0,t1]内，CH(C)的运动轨迹为一条直线，运动轨迹的表达式见式(8)，其运动轨迹如图3所示。

PC(α)=α·Δt(vA-vB)。

(8)

2)碰撞检测 应用GJK算法进行碰撞检测的主要步骤是计算一段时间内CSO距离原点的最小距离。由于物体为匀速直线运动，具有空间连续性，由图3可知，若未发生碰撞，原点在CSO的外面，距CSO的最小距离等于距CSO运动轨迹最外面边界的距离。若发生碰撞，则原点位于CSO内部，一定在CSO内某两点运动轨迹之间。因此，计算CSO距原点的最小距离可转化为计算原点到CSO边界上点的运动轨迹的距离，可根据式(9)-式(11)求得距离。

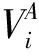
(9)

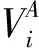
(10)

d=‖Ok‖。

(11)

算法的伪代码如下所示：

Algorithm1 collisiondetectinv←＂arbitrarypointinC＂；W←∅；do{ (a，d，Ok，O＿in)←subdistance＿algorithm(Wk) ifO＿inreturnTRUE； w←SA-B(-Ok)； if‖Ok‖2+SA-B(-Ok)g(-Ok)=0thenexit＿loopendif Y←W∪{w}； if(d>0)returnFALSE；}whileTRUE

在迭代过程中，若Wk包含一个点，那么，距离子算法返回a,d,Ok,O_in=false。

如果Wk包含2个点，首先检查O是否在2个点的运动轨迹之间，如果运动轨迹之间包含原点，令O_in=true，并停止迭代，返回“A和B碰撞”。

2.2碰撞响应

碰撞响应的最终目的是当检测到两物体发生碰撞时，根据环境要求及时调整物体状态，避免发生穿透现象。因此，碰撞响应需要计算得到碰撞发生时物体的位置。

在时间区间[t0,t1]内，A和B的位移向量分别为T1和T2。由式(5)和式(6)可得，

T1=Δt·vA,T2=Δt·vB。

为简化过程，令物体B处于相对静止状态，因此物体A的相对位移向量(相对于物体B)定义为T=T1-T2。因此，T=Δt·(vA-vB)。

由定义可得，C=A-B。在t0时刻，C0=A0-B；在t1时刻，C1=A1-B，又有A1=A0+T。由此，可得C1=C0+T。也就是说，在时间区间[0,1]内，CH(C)是运动的，其位移向量与物体A的相对位移向量相同，均为T[13]。

由于CH(C)是运动的，原点是静止的。为进一步简化计算过程，考虑CH(C)是静止的，原点相对于CH(C)是运动的，其相对位移向量为-T，如图4所示。

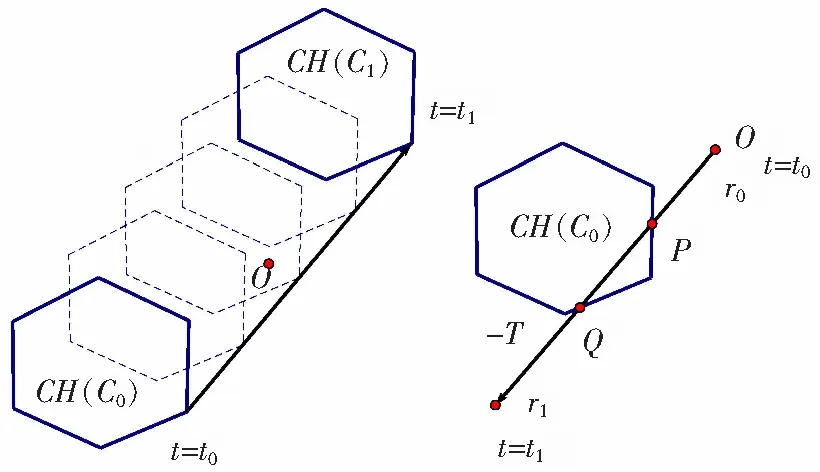
图4 CSO与原点的相对位移Fig.4 Relative displacement of CSO and origin

由图4可知，碰撞发生时运动物体A的位置可由t0时刻的位置加上一个位移向量得到。这个位移向量的大小和方向与原点相对路径所在射线与CSO的第一个交点指向原点的向量相等。因此，在碰撞响应中，最主要的就是要确定射线与CSO的第1个交点[13]。

文献[17]提出了ray-casting算法来获得射线与凸体的交点，本文将此算法进行推广，计算原点相对路径所在射线与CSO的第1个交点。

定义射线OR用式(12)来表示。

R={s+λr，λ≥0}。

(12)

式中：s为射线OR的源点；r表示射线OR的方向。在本文中，由于射线的源点为原点，所以射线OR可表示为

R={λr，λ≥0}。

(13)

求射线OR与凸体CSO的第1个交点可转化为求使得点x=λr在凸体内部的最小的λ，记为λ*，求得的点记为x*。

算法如下所示。

令k为迭代次数。首先，令λ0等于0，x0为射线的初始点。定义c为凸体CSO上距离x最近的点，c可以通过GJK算法求得；计算n=x-c，若‖x-c‖>ε，则按式(14)和式(15)方式更新λ0和x0。

(14)

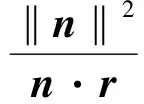
(15)

假设当迭代到第k+1次时，‖x-c‖<ε，那么可认为xk+1与x*重合，即为射线OR与凸体CSO的第1个交点。算法的伪代码如下所示。

Algorithm2diatancebasedraycastλ←0；x←s；n←0；c←＂thepointofCclosesttox＂；begin n←x-c； in‖n‖<ε；{ x∗←x； break；} λ←λ-‖n‖2/n·r； x←s+λr； c←＂thepointofCclosesttox＂；end； returnx∗；

3 仿真及分析

本文以Microsoft Visual Studio 2010为开发平台，标准C++语言实现算法。实验环境设置如下：操作系统为Microsoft Windows7；CPU为Intel Core i3 M 330，2.13 GHz；内存为4 GB。

为验证本文算法的有效性及实时性，建立三维场景复杂度不同的场景进行测试。选取具有多个大小不同的正方体作为实验对象，正方体由程序生成，并且每个正方体移动方向和速度为随机生成，当2个正方体发生碰撞时，物体的颜色由绿色变为红色，当两物体分开后，物体颜色恢复绿色，如图5所示。通过改变场景中正方体的个数来控制场景复杂度。当场景中正方体数量为50个时，碰撞检测时间约为0.5 ms，当正方体数量增加到500个时，碰撞检测时间只有4.9 ms，能够满足实时性要求。

图5 不同复杂度场景下的碰撞检测Fig.5 Collision detection in scene of different complexity

通过在不同复杂度下的场景的测试，对本文的快速碰撞检测算法FCCD和张应中等提出的LCCD算法[13]的碰撞检测效率进行了比较，并记录了一段时间内的平均检测时间，仿真实验结果如图6所示。通过图6中的仿真实验测试数据可知：在同一场景下，本文碰撞检测效率与LCCD算法比较，实时性有较大提高，能够满足虚拟场景中对碰撞检测的实时性要求。

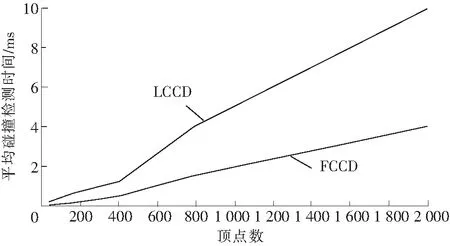
图6 不同算法平均碰撞检测时间比较Fig.6 Average collision detection time comparison of different algorithms

4 结 语

本文提出了一种基于GJK的凸体快速碰撞检测算法，该算法针对多个运动物体，利用GJK算法在有限步骤内计算两物体间的最小距离，检测是否发生碰撞，并利用ray-casting算法计算得到两物体发生碰撞的精确位置，根据环境要求及时做出相应的响应。仿真实验结果表明，本文提出的算法具有较快的响应速度和较高的检测精度。下一步将针对凸体之间的非线性运动及非凸体之间的连续碰撞检测进行研究。

/

[1] 周湛学,张文苑,杜永祚,等.虚拟仪器技术及其应用初探[J].河北科技大学学报,2002,23(4): 71-75. ZHOU Zhanxue,ZHANG Wenyuan,DU Yongzuo,et al.Research of fictitious instrument technique and its application[J].Journal of Hebei University of Science and Technology,2002,23(4):71-75.

[2] 杨 仙,李国昌,刘瑞涛.轧辊虚拟制造技术研究[J].河北科技大学学报,2006,27(1): 86-88. YANG Xian,LI Guochang,LIU Ruitao.Research on virtual manufacturing technology of rollers[J].Journal of Hebei University of Science and Technology,2006,27(1): 86-88.

[3] 张 博,王 南,王泽仁.基于SolidWorks的摄影机器人虚拟设计与运动分析[J].河北工业科技,2014,31(1):24-26. ZHANG Bo,WANG Nan,WANG Zeren.Virtual design and movement analysis of the photography robot based on SolidWorks[J].Hebei Journal of Industrial Science and Technology,2014,31(1):24-26.

[4] 张莉莎,李小龙,孙 政,等.基于Pro/E的机械零部件三维动态序列装配技术研究[J].河北工业科技,2014,31(2):164-167. ZHANG Lisha,LI Xiaolong,SUN Zheng,et al.Research on assembly technology of three-dimensionaldynamic sequence based on Pro/E[J].Hebei Journal of Industrial Science and Technology,2014,31(2):164-167.

[5] 邹益胜,丁国富,许明恒,等.实时碰撞检测算法综述[J].计算机应用研究,2008,25(1):8-12. ZOU Yisheng,DING Guofu,XU Mingheng,et al.Survey on real-time detection algorithms[J].Application Research of Computers,2008,25(1):8-12.

[6] 黄通浪,唐 敏,董金祥.一种快速精确的连续碰撞检测算法[J].浙江大学学报(工学版),2006,40(6):1051-1055. HUANG Tonglang,TANG Min,DONG Jinxiang.Fast and accurate continuous collision detection between rigid bodies[J].Journal of Zhejiang University (Engineering Science),2006,40(6):1051-1055.

[7] 王 季,翟正军,蔡小斌.分布式虚拟环境中基于扫描体的碰撞检测研究[J].计算机工程,2007,33(15): 55-57. WANG Ji,ZHAI Zhengjun,CAI Xiaobin.Collision detection algorithm based on swept volume in distributed virtual environments[J].Computer Engineering,2007,33(15): 55-57.

[8] 徐芝琦,陈志杨,叶修梓,等.基于扫描跟踪元的快速碰撞检测[J].计算机辅助设计与图形学学报,2008,20(11): 1417-1424. XU Zhiqi,CHEN Zhiyang,YE Xiuzi,et al.Fast collision detection based on swept tracing primitives[J].Journal of Computer-Aided Design & Computer Graphics,2008,20(11): 1417-1424.

[9] FOGEL E,HALPERIN D.Exact minkowski sums of convex polyhedra[A].Proceedings of the 21st Annual Symposium on Computational Geometry,SCG'05[C].Pisa: Association for Computing Machinery,2005.382-383.

[10] TANG M,KIM Y J,MANOCHA D.C2A: Controlled conservative advancement for continuous collision detection of polygonal models[A].2009 IEEE International Conference on Robotics and Automation (ICRA)[C].Piscataway: IEEE,2009.849-854.

[11] GILBERT E G,FOO C P.Computing the distance between general convex objects in three-dimensional space[J].IEEE Transactions on Robotics and Automation,1990,6(1): 53-61.

[12] OH S,HWANG S.A GJK based real-time collision detectionalgorithm for moving objects[A].Advances in Cognitive Neurodynamics ICCN 2007[C].Berlin:Springer Netherlands,2008.817-820.

[13] 张应中,范 超,罗晓芳.凸多面体连续碰撞检测的运动轨迹分离轴算法[J].计算机辅助设计与图形学学报,2013,25(1):7-14. ZHANG Yingzhong,FAN Chao,LUO Xiaofang.Separating-axis calculation of motion path for continuous collision detection of convex polyhedrons[J].Journal of Computer-Aided Design & Computer Graphics,2013,25(1):7-14.

[14] ERICSON C.Real-time Collision Detection [M].Boca Raton:CRC Press,2004.

[15] BERNABEU E J.Continuous distance computation for motions with constant accelerations[A].2010 IEEE International Conference on Robotics and Automation,ICRA 2010[C].Piscataway: IEEE,2010.4028-4034.

[16] BERNABEU E J,VALERA A,GOMEZ-MORENO J.Distance computation between non-holonomicmotions with constant accelerations[J].International Journal of Advanced Robotic Systems,2013,10:1-8.

[17] Van den BERGEN G.Ray casting against general convex objects with application to continuous collision detection [EB/OL].http://www.dtecta.com,2004-07-02.

A GJK-based fast continuous collision detection for convex objects

LIU Li1, ZHANG Guoshan1, BING Zhigang2, LIU Min1

(1.School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China; 2.Tianjin Key Laboratory of Information Sensing and Intelligent Control, Tianjin 300222, China)

This paper presents a fast continuous collision detection algorithm to dealing with moving multiple convex objects within a period of time, which is based on the Gilbert-Johnson-Keerthi algorithm. The algorithm is determined by whether the minimum distance between the two objects within a period of time is zero to detect the occurrence of a collision. First, the algorithm utilizes GJK algorithm to calculate the minimum distance between the two objects and to detect the collision in finite steps. If two objects collide, then, determine the precise collision position of two objects based on the ray-casting algorithm, and respond according to the environmental requirements, adjust two objects' location. The simulation results show that this algorithm has high real-time and accurate characteristics for continuous collision detection between multiple moving objects.

continuous collision; Gilbert-Johnson-Keerthi(GJK) algorithm; moving objects; collision detection; convex objects

2014-06-09；

2014-07-16；责任编辑：李 穆

国家自然科学基金(61074088)

刘 丽(1990-)，女，河北石家庄人，硕士研究生，主要从事虚拟现实、计算机图形学方面的研究。

张国山教授。E-mail：zhanggs@tju.edu.cn

1008-1542(2014)05-0440-07

10.7535/hbkd.2014yx05006

TP391.9

A

刘 丽，张国山，邴志刚，等.基于GJK的凸体快速连续碰撞检测研究[J].河北科技大学学报,2014,35(5):440-446.

LIU Li,ZHANG Guoshan,BING Zhigang,et al.A GJK-based fast continuous collision detection for convex objects[J].Journal of Hebei University of Science and Technology,2014,35(5):440-446.