平面欠驱动两杆柔性机械臂的全局稳定控制

葛 洋，张安彩，韩丹阳，冯凯强，王 琛

(临沂大学汽车学院，山东临沂 276000)

平面欠驱动两杆柔性机械臂的全局稳定控制

葛 洋，张安彩，韩丹阳，冯凯强，王 琛

(临沂大学汽车学院，山东临沂 276000)

针对平面欠驱动两杆柔性机械臂，该文提出一种新的控制策略，实现了机械臂的全局稳定控制目标。首先,为机械臂系统引入一个同胚坐标变换，将其变换为一个结构简单的新系统；然后,将新系统分离为线性和非线性2个部分，利用等价输入干扰的概念为新系统设计控制器，以实现新系统的全局稳定控制目标,并通过坐标变换的同胚性使原机械臂系统的全局稳定控制问题得以解决。该文所提控制方法仅需利用机械臂的位置量信息设计控制器，这不仅能降低控制系统成本，而且还能有效避免速度噪音对控制性能的影响。数值仿真结果显示,所提的控制策略在机械臂系统的稳定运动过程及稳定时间等性能方面，均能达到令人满意的控制效果。

欠驱动机械系统；柔性机械臂；稳定控制；等价输入干扰

1 欠驱动机械系统简介

欠驱动机械系统是控制输入个数少于自由度个数的一类非线性系统[1-2]。驱动器的减少使这类系统具有质量轻、能耗低、运动灵活等优点，目前它们已经被广泛应用于工业、农业、交通运输、航空航天等领域中，在人们的生活中发挥着越来越重要的作用。

近年来，学者们对欠驱动机械系统的控制理论进行了广泛深入的研究[3-4]。作为欠驱动机械系统的一类典型代表，欠驱动机械臂成为学者们研究的热点[5-7]，这其中两杆体操机器人Acrobot[8]的研究尤其引人关注。 Acrobot是一个在垂直平面内运动的两连杆机械臂，它是一个体操运动员在单杠上运动的简化模型。 为模拟体操运动员由上杠到垂直倒立的过程，学者们最常讨论的控制目标是将Acrobot由垂直向下的最低点摇起，并最终稳定在垂直向上的最高点处。 然而要实现这个控制目标并非易事，这主要是由于Acrobot 是一个具有二阶非完整约束的[9]、并且不能严密反馈线性化的[10]复杂非线性系统所致。 为有效实现Acrobot 的上述控制目标，目前比较常用的策略是将它的整个运动空间划分为摇起区和平衡区，然后分别为这两个子区域设计控制器，并最终通过摇起控制器和平衡控制器的切换实现稳定控制。 基于这种分区切换控制策略，学者们提出了很多种控制方法，这包括部分反馈线性化法[11]、模糊控制法[12]、能量控制法[13]等。

与在垂直平面内运动的机械臂相比，水平面内运动的机械臂在工业制造、外科手术等领域具有更广泛的应用背景[14-15]。与欠驱动Acrobot 相对应的水平面内运动的机械臂常称之为平面欠驱动两杆机械臂，这个机械臂的机械构造与Acrobot 一样，不同之处是它在一个水平面内运动，并且它的运动过程不受重力作用的影响。 虽然机械构造与Acrobot一样，但平面欠驱动两杆机械臂的控制却比Acrobot 的控制难的多，这主要由两方面原因造成的：第一，重力作用的缺失使运动平面上的每个点都成为机械臂平衡点，并且机械臂系统在每个平衡点周围都不能局部线性能控；第二，正如文献[16]所指出那样，平面欠驱动两杆机械臂甚至不能小范围局部能控的，因此很难将机械臂控制到期望的目标位置。 为有效解决平面欠驱动两杆机械臂的控制问题，学者们在机械臂的机械构造方面提出了一些有益的建议，如文献[17]在机械臂的第一关节处加装了一根弹簧，形成了弹簧耦合型欠驱动两杆机械臂，并提出了一种基于无源性的稳定控制方法。 由于弹簧的成本远低于驱动器,因此这种在机械臂上加装弹簧的方法是控制平面欠驱动机械臂最经济有效的方法。 事实上，这种加装弹簧的做法是比较符合实际的，因为机械臂或多或少都存在柔性，这种做法是将机械臂的柔性通过弹簧的弹力来体现。 因此，学者们也常将弹簧耦合型机械臂视为柔性机械臂的简化模型。

目前，对平面欠驱动两杆柔性机械臂的相关研究还比较少，很少有文献来讨论这类机械臂的稳定控制问题，正是此背景促使了本文研究工作的展开。针对平面欠驱动两杆柔性机械臂，本文提出一种新的控制策略来实现机械臂的全局稳定控制目标。这种控制策略的设计过程包含如下2个阶段：

1) 为机械臂系统引入一个同胚坐标变换，将其变换为一个结构简单的新系统；

2) 将新系统的线性部分和非线性部分分离，通过将非线性部分视为虚拟扰动的方法来引入等价输入干扰的概念，并利用等价输入干扰来构造新系统的全局稳定控制器，最后通过坐标变换的同胚性保证原系统全局稳定控制目标的实现。

上述控制策略仅需利用机械臂的位置量信息便能实现系统的全局稳定控制目标，这不仅能降低控制系统成本，而且还能有效避免速度噪音对控制性能的影响，具有重要的实际应用价值。

2 动力学模型和坐标变换

欠驱动两连杆柔性机械臂的简化模型如图1所示，其中的参数与变量的定义如下(i=1,2):

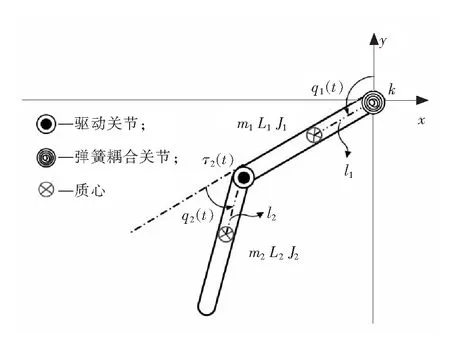
图1 欠驱动两连杆柔性机械臂Fig.1 Underactuated horizontal two-link flexible manipulator

mi为第i杆的质量；Li为第i杆的长度；li为第i关节到第i杆质心的距离；

Ji为第i杆的转动惯量；k为弹簧的弹性系数；τ2(t)为第二关节处的控制输入力矩；

q1(t)为第一杆相对y轴的转动角度；q2(t)为第二杆相对于第一杆的转动角度。

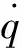
(1)

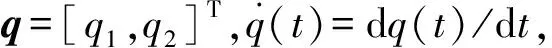
(2)

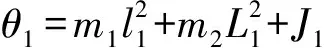
(3)

运动方程 (3)简化为如下的标准形式：

(4)

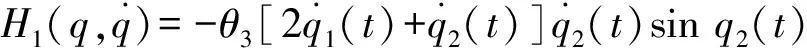
为完成上述的控制目标，首先为系统 (4) 引入一个可逆的同胚坐标变换

根据式(3)第1个式子，不难验证坐标变换T将系统 (4) 变为

(5)

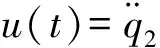
(6)

式中det(M(q2))=M11(q2)M22-M12(q2)M21(q2)>0为矩阵M(q2)的行列式。 现记z(t)=[z1(t),z2(t),z3(t),z4(t)]T。 由于T是一个可逆连续的坐标变换，故得ξ(t)=0等价于z(t)=0。因此,原系统 (4) 在零点处的全局稳定控制问题就转化为变换后系统 (5) 在零点处的全局稳定控制问题。基于此，以下章节主要来讨论如何设计控制器u(t)使系统(5)全局渐近稳定在z(t)=0处。

3 基于等价输入干扰的控制系统设计

由于本文假设只有位置变量q(t)=[q1(t),q2(t)]T可测，故根据坐标变换T的表达式知只有z1(t)与z3(t)的信息可测。选择z1(t)与z3(t)作为系统 (5) 的输出量，并将式(5) 记为式(7)形式：

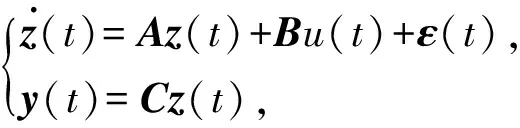
(7)

式中：

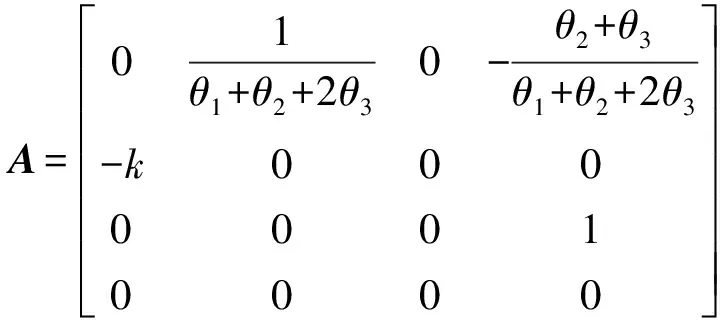
不难发现，式(7)中的ε(t)为该系统的非线性高阶项。 在本文的研究中，将ε(t)作为系统 (7) 的一个虚拟扰动来处理。 经过简单计算得，(A,B)完全能控，(C,A)完全能观测且系统(A,B,C)没有零点。 根据文献[18]中的结论知，在输入端存在一个与扰动项ε(t)相对应的等价输入干扰εe，并且相应的系统方程为

(8)

为描述方便，仍采用符号z来表示系统 (8) 的状态变量。为系统(8) 构建一个基于等价输入干扰的控制系统，其结构如图2所示，它由被控系统、扰动估计器、反馈控制器与状态观测器4部分组成。 下面来详细说明等价输入干扰估计器，反馈控制增益K以及观测器增益L的设计。

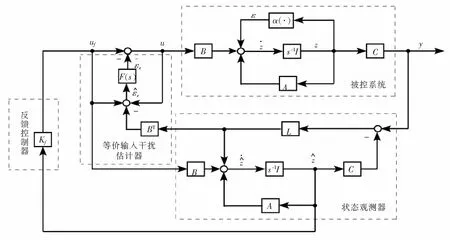
图2 基于等价输入干扰的控制系统结构图Fig.2 Configuration of equivalent-input-disturbance (EID)-based control system

3.1等价输入干扰估计器设计

为系统 (8) 构造如下一个全维状态观测器：

(9)

(10)

式中

(11)

联立式(9)和式(10)可得：

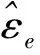
(12)

在式(12)两端同时乘以BT并化简得

(13)

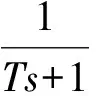
(14)

3.2反馈控制增益设计

将状态反馈控制增益Kf设计为

(15)

式中：Q>0,R>0为正定的权矩阵。由于(A,B)能控且A-LC是稳定的，故易知反馈控制律

(16)

可使系统(8)渐近稳定在z(t)=0处。 从而知控制律

(17)

可将系统 (8) 的输出渐近稳定在零点，即z1(t)→0，z3(t)→0。再由系统 (5) 的表达式推得，当z1(t)→0，z3(t)→0时z2(t)→0,z4(t)→0。这说明控制律 (17) 可将系统 (5)渐近稳定在z(t)=0处。

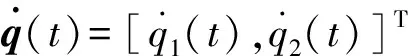
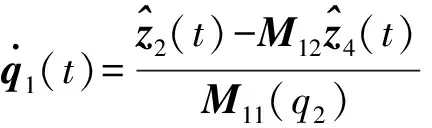
(18)

3.3状态观测器增益设计

对于式(14)中给定的低通滤波器F(s)，本小节来论述观测器增益L的设计，以保证整个控制系统的稳定性。 由式(9)，式(10)和式(11)得

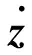
(19)

再由式(13) 和式(17)得

(20)

G(s)=1-BTLC[sI-(A-LC)]-1B=BT(sI-A)[sI-(A-LC)]-1B。

(21)

如文献[16]中所述，为保证整个系统的稳定性，观测器增益L需要满足A-LC稳定且

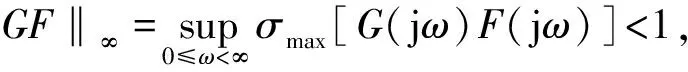
(22)

式中σmax[·]为最大的奇异值函数。这里将L设计为如下形式，见式(23):

(23)

式中QL>0,RL>0为正定的加权矩阵,ρ>0为一个标量。由于(A,C)是可控的,那么(CT,AT)是可观测的。因此,由式(23) 设计的L可以使A-LC稳定。另一方面，考虑到系统(A,B,C)的对偶系统为

(24)

由于系统 (24) 的控制输入的数目要大于控制输出的数目，并且AT-CTKρ是稳定的，因此，根据文献[19]中定理1和定理3的结论可有

(25)

注意到

[sI-(A-LC)]-1B=[BT[sI-(AT-CTKρ)]-1]T

为G(s)的一部分，故由式(25)可知，当参数的值很大时可保证条件式 (22) 是成立的。

4 数值仿真实例

为验证本文所提控制方法的有效性，在Matlab/Simulink环境下搭建欠驱动两杆柔性机械臂的模型进行数值仿真,机械臂的物理参数取为

(26)

此外,式 (14),式(15)和式(23) 中的控制参数分别选为

(27)

其中In表示一个n×n单位矩阵。在这些参数的条件下，通过利用Matlab函数lq r和norm计算得

显然,条件(22)是满足的。 另外，机械臂的初始仿真条件选为

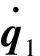
(28)

图3给出了在这一初始条件下的数值仿真结果。 结果表明,在控制器 (7) 和控制器(20) 的作用下，欠驱动两杆柔性机械臂能够被快速稳定在x(t)=0处，整个稳定过程比较平滑，稳定时间也不超过6 s，所有这些均说明了本文所提控制方法有效性。

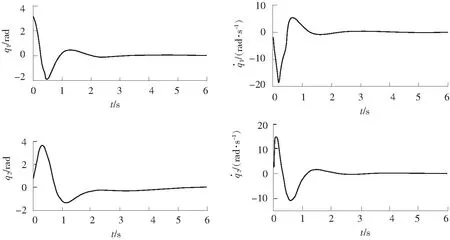
图3 欠驱动两杆柔性机械臂角度和角速度的仿真结果Fig.3 Simulation results of angles and angular velocities for underactuated horizontal two-link flexible manipulator

5 结 论

针对平面欠驱动两杆柔性机械臂，在只有机械臂的位置量信息可测的条件下，本文提出了一种有效的全局稳定控制方法。这种控制方法的设计过程共包含2个阶段。首先，通过一个同胚坐标变换将原机械臂系统转化为一个结构简单的非线性系统。 然后,将新系统的线性部分和非线性部分分离，通过将非线性部分视为虚拟扰动的办法来引入等价输入干扰的概念，并利用等价输入干扰来构造控制器，以使新系统全局渐近稳定在原点。由于原系统和新系统之间的变换是同胚的，从而使原机械臂系统的全局稳定控制问题得以解决。 仿真实例验证了所提控制方法的有效性。

/

[1] GRIZZLE J W，MOOD C H, CHEVALLEREAU C. Nonlinear control of mechanic an unactuated cyclic variable [J]. IEEE Transaction on Automatic Control, 2005, 50(8): 559-576.

[2] LIU Yang,YU H. A survey of underactuated mechanical systems[J]. IET Control Theory & Application, 2013, 7(7): 921-935.

[3] XIN Xin. On simultaneous control of the energy and actuated variables of underactuated mechanical systems-example of the acrobot with counterweight[J]. Advanced Robotics, 2013, 27(12): 959-969.

[4] LI Maoqing, HUO Wei. Controller design for mechanical systems with underactuation degree one based on controlled Lagrangians method[J]. International Journal of Control, 2009, 82(9): 1747-1761.

[5] ANGELI D. Almost global stabiliation of the inverted pendulum via continuous state feedback[J]. Automatica, 2001, 37(7): 1103-1108.

[6] QAISER N, IQBAL N. Exponential stabilization of the inertia wheel pendulum using dynamic surface control [J]. Journal of Circuits,Systems and Computers, 2007, 16(1): 81-92.

[7] SRINIVASAN B, HUGUENIN P, BONVIN D. Global stabilization of an invert pendulum-Control strategy and experimental verification[J]. Automatica, 2009, 45(1): 265-269.

[8] 程红太，赵旖旎，张晓华．Acrobot动态伺服控制及其对称虚约束方法研究[J]．自动化学报，2010, 36(11)：1594-1600． CHENG Hongtai, ZHAO Yini, ZHANG Xiaohua. Dynamical servo control and symmetrical virtual constraints method for the Acrobot[J]. Acta Automatica Sinica, 2010, 36(11): 1594-1600.

[9] ORIOLO G, NAKAMURA Y. Control of mechanical systems with second-order nonholonomic constraints: underactuated manipulators[A].Proceedings of the 30th IEEE Conference on Decision and Control[C]．Brighton:[s.n.], 1991.2398-2403.

[10] HUNT R, SU R, MEYER G. Global transformations of nonlinear systems [J]. IEEE Transactions on Automatic Control, 1983, 28(1): 24-31.

[11] SPONG M W. The swing up control problem for the Acrobot[J].IEEE Control Systems Magazine,1995, 15(1): 49-55.

[12] LAI X, SHE J, YASUHIRO O, et al. A fuzzy control strtegy for Acrobot combining model-free and model-based control [J]. IET Control Theory and Applications, 1999, 146(6)：505-510.

[13] XIN X, KANEDA M.Analysis of the energy-based swing-up control of the acrobot[J]. International Journal of Robust Nonlinear Control, 2007, 17(16): 1503-1524.

[14] 吕 晋，张 俊，王 南．移动机器人模块化机械臂运动学分析[J]．河北工业科技，2013, 30(5)：333-337． LYU Jin, ZHANG Jun, WANG Na. Kinematics analysis of modular manipulators of mobile robot[J]. Hebei Journal of Industrial Science and Technology, 2013, 30(5): 333-337.

[15] 张 博，王 南，王泽仁．基于SolidWorks的摄影机器人虚拟设计与运动分析[J]．河北工业科技，2014, 31(1)：24-26． ZHANG Bo, WANG Na, WANG Zeren. Virtual design and movement analysis of the photography robot based on SolidWorks[J]. Hebei Journal of Industrial Science and Technology, 2014, 31(1): 24-26.

[16] BULLO F, LEWIS A D, LYNCH K M. Controllable kinematic reductions for mechanical systems:conceepts,conputational tool and examples[A].Proceedings of International Symposium on Mathematical Theory of Netwarks and Systems[C]．Indiana:[s.n.], 2002.1-16.

[17] POPESCU C, WANG Y, ROTH Z. Passivity based control of spring coupled underactuated horizontal double pendulum[A].Proceedings of Florid Conference of recent Advances in Robotics[C]. Florida:[s.n.],2003.1-17.

[18] SHE J, FANG M, OHYAMA Y,et al. Improving disturbance-rejection performance based on an equivalent-input-disturbance approach[J]. IEEE Transactions on Industrial and Electronics, 2008, 55(1): 1380-1389.

[19] KIMURA H. A new approach to the perfect regulation and the bounded peaking in linear multivariable control systems[J].IEEE Transactions on Automatic Control, 1981, 26(1): 253-270.

Global stabilization control of underactuated horizontal two-link flexible manipulator

GE Yang, ZHANG Ancai, HAN Danyang, FENG Kaiqiang, WANG Chen

(School of Automobile Engineering, Linyi University, Linyi Shandong 276000, China)

This paper presents a new control strategy for an underactuated horizontal two-link flexible manipulator (HTFM) to realize the global stabilization. First, a homeomorphous coordinate transformation is introduced to the original manipulator system to create a new simple nonlinear system. Then, the new system is divided into the linear and nonlinear parts, and the idea of equivalent-input-disturbance (EID) is used to design a controller that globally and asymptotically stabilizes the new system as goal. The global stabilization control problem for the underactuated HTFM is soloved by the fact that the transformation is homeomorphous. The presented control method just adopts the position information of HTFM to design the stabilizing controller, which can not only reduce the cost of the control system, but also avoid the influence of velocity noises on the control performance effectively. The simulation results show that the stabilizing motion process, stabilizing time and other performances of the underactuated HTFM can achieve satisfactory results.

underactuated mechanical systems; flexible manipulator; stabilizing control; equivalent input disturbance

2014-04-16；

2014-06-17；责任编辑：李 穆

国家自然科学基金(61304023)

葛 洋(1993- )，男，山东莒南人，主要从事机器人控制的相关研究。

张安彩博士，讲师。E-mail: zhangancai@lyu.edu.cn

1008-1542(2014)05-0428-07

10.7535/hbkd.2014yx05004

TP273

A

葛 洋，张安彩，韩丹阳，等.平面欠驱动两杆柔性机械臂的全局稳定控制[J].河北科技大学学报,2014,35(5):428-434.

GE Yang，ZHANG Ancai，HAN Danyang，et al.Global stabilization control of underactuated horizontal two-link flexible manipulator[J].Journal of Hebei University of Science and Technology,2014,35(5):428-434.