M-纤维式同伦扩张性质及其应用
郑芳婷, 赵 浩
(华南师范大学数学科学学院,广州 510631)


我们称(α,β)为M-纤维式映射, 记作(α,β):(X1,p1,Y1)→(X2,p2,Y2).对象p:X→Y称为M-纤维式空间,记作(X,p,Y).范畴MAP中态的合成为各分量映射的分别合成,即:
(α,β)(θ,φ):(X1,p1,Y1)→(X2,p2,Y2),
(α,β)(θ,φ)=(αθ,βφ).
易见,范畴Top为范畴MAP的子范畴.这种关系暗示可将范畴Top中的性质在范畴MAP中作推广, 或者把范畴MAP里的命题特殊化到范畴Top进行刻画说明.在范畴Top中,设空间X的一个子空间为A,如果任意映射X×{0}∪A×I→Y可以扩张成映射X×I→Y,则称空间偶(X,A)具有同伦扩张性质[3].同伦扩张性质作为代数拓扑的一个基本概念,是研究的重要对象.
本文将范畴Top中的同伦扩张性质推广到范畴MAP进行刻画, 并论证若干相关性质.
文献[3]定义了范畴Top的同伦扩张并给出部分应用, 但未给出严格证明. James系统地阐述了纤维式同伦论,描述了与之对偶的空间下范畴同伦论[4], 并分别介绍了纤维式一般拓扑理论与纤维式稳定同伦论[5]. Buhagiar[2]将所有连续映射都处理成对象建立起M-纤维式范畴,并探讨纤维式的一般拓扑,推广了纤维式一般拓扑的理论. Hotta与Miwa[6]系统地建立起范畴MAP的同伦论, 定义了M-纤维式纤维化,由此推广了文献[7]中关于纤维范畴的部分重要命题.文献[8]进一步对M-纤维式纤维化的特征和诱导纤维化进行了研究. 文献[9]考虑了此范畴中对象的H-性质和CoH-性质. 本文将先建立起M-纤维式范畴中的同伦扩张性质并给出其若干应用,同时将上述命题都特殊化到范畴Top中进行刻画,由此对应得出关于拓扑范畴中同伦扩张性质的相关结论.
设A0为A的子空间,X0为X的子空间,以下是本文所得主要结论.
定理1 ((A,p,X),(A0,p0,X0))具有同伦扩张性质等价于(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)是(A×I,p×id,X×I)的M-纤维式收缩核.

定理3 若(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)是(A×I,p×id,X×I)的M-纤维式形变收缩核,(f1,f2),(g1,g2):(A0,p0,X0)→(E,f,B)是贴附映射,且(f1,f2)≃F(g1,g2).则(E,f,B)(f1,f2)(A,p,X)≃M(E,f,B)(g1,g2)(A,p,X)rel(A0,p0,X0).
定理4 映射(α,β):(A,p,X)→(E,f,B)为同伦等价当且仅当(A,p,X)是M-纤维式映射柱M(α,β)的形变收缩核.故M-纤维式空间(A,p,X)与(E,f,B)同伦等价当且仅当存在一个M-纤维式空间同时以(A,p,X)和(E,f,B)为M-纤维式形变收缩核.
上述各定理中所出现的符号说明见第1节.
1 M-纤维式同伦扩张性质
作为拓扑范畴中同伦扩张性质的自然推广,本节将在范畴MAP中定义出M-纤维式同伦扩张性质.此处先对后文所涉及的定义和记号进行声明.

定义1 (α,β):(A,p,X)→(E,f,B)是M-纤维式映射. (A×IE,p×idf,X×IB)以等价关系a×{1}~α(a),x×{1}~β(x)(aA,xX)所作商空间定义为M-纤维式映射柱:
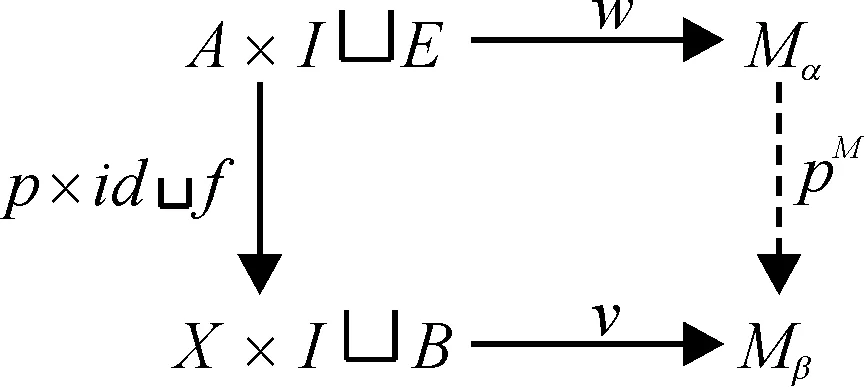
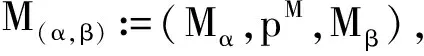
定义2 (A0,p0,X0)是(A,p,X)的子集,(α,β):(A0,p0,X0)→(E,f,B)为M-纤维式映射.定义(a0,p,x0)与(α,β)(a0,p,x0)=(e,f,b)粘合得到的(A,p,X)(E,f,B)的商空间为借助映射(α,β):(A0,p0,X0)→(E,f,B)把(A,p,X)贴附到(E,f,B)的M-纤维式贴附空间,记作(A,p,X)(α,β)(E,f,B).
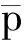

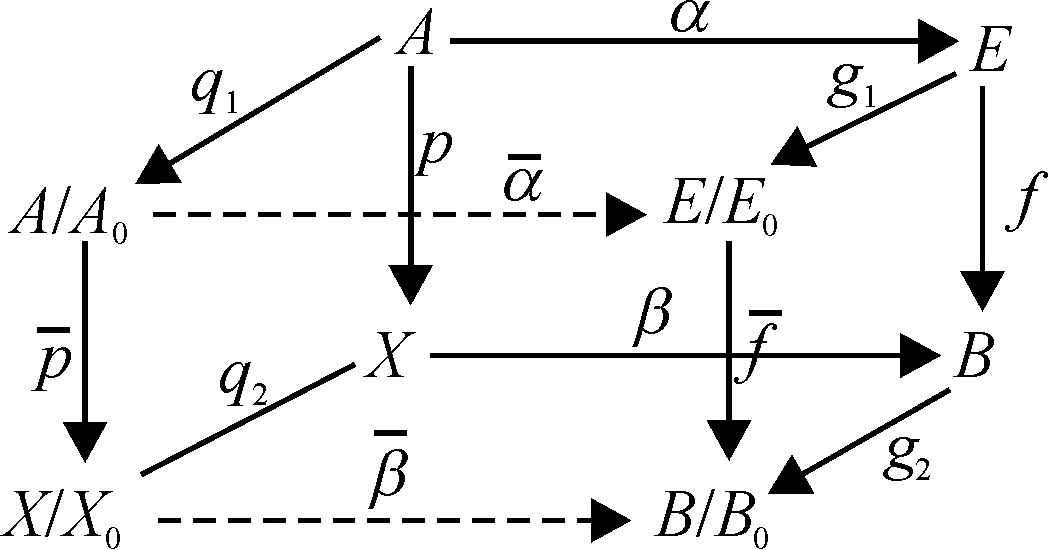
根据范畴Top的同伦扩张和范畴MAP的概念定义M-纤维式同伦扩张性质如下:
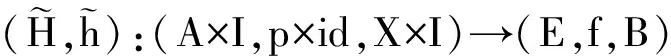
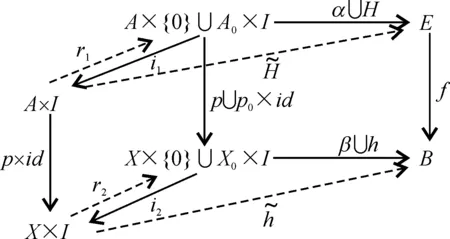
例1 设A0为CW复形A的子复形,X0为CW复形X的子复形,则空间偶(A,A0)与(X,X0)具有同伦扩张性质. 若令映射p0:A0→X0与p:A→X为单值映射且映为X中的相同单点,则((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质.
选取定义5中的M-纤维式映射(α,β)为M-纤维式恒同映射,则可得定理1.
定理1的证明(必要性)由注记1,((A,p,X),(A0,p0,X0))具有同伦扩张性质即当任意映射
(ω,η):(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)→
(E,f,B)
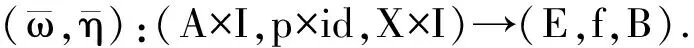
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)
上的恒同映射能扩张成:
(R,r):(A×I,p×id,X×I)→
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I).
(充分性)记收缩映射为
(R,r):(A×I,p×id,X×I)→
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I),
对于任意给定映射
(ω,η):(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)→
(E,f,B),
有:
(ω,η)
(E,f,B),
由注记1可知((A,p,X),(A0,p0,X0))具有同伦扩张性质.
推论1[3](X,A)具有同伦扩张性质等价于X×{0}∪A×I是X×I的收缩核.
以下给出具体的形变收缩过程,使得上述关于M-纤维式收缩核的等价条件进一步加强为M-纤维式形变收缩核.
性质1 ((A,p,X),(A0,p0,X0))具有同伦扩张性质等价于(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)是(A×I,p×id,X×I)的M-纤维式形变收缩核.
此命题充分性由定理1易见,故此处只给出必要性的证明.
由((A,p,X),(A0,p0,X0))为具有同伦扩张性质的偶对可得收缩映射:
(R,r):(A×I,p×id,X×I)→
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I).
不妨以分量形式记R(a,t)=(R1(a,t),R2(a,t)),r(x,t)=(r1(x,t),r2(x,t)),其中,


则可以得到形变收缩(H,h):(X×I×I,p×id×id,B×I×I)→(X×I,p×id,B×I):
H(a,t,s)=((1-s)t+sR1(a,t),R2(a,ts))
h(x,t,s)=((1-s)t+sr1(x,t),r2(x,ts)).
推论2[3](X,A)具有同伦扩张性质等价于X×{0}∪A×I是X×I的形变收缩核.
下面找出和M-纤维式同伦扩张性质密切相关的“M-纤维式闭映射柱邻域”.
性质2 对于M-纤维式偶对((A,p,X),(A0,p0,X0)),若可找到M-纤维式映射(α,β):(BA,pB,BX)→(A0,p0,X0)及同胚(,ξ):M(α,β)→(NA,pN,NX),满足(NA,pN,NX)为(A0,p0,X0)的M-纤维式闭邻域,且|A0=idA0,ξ|X0=idX0,则((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质.记AN的边界(BA)为的边界ξ(BX)为纤维式空间(NA,pN,NX)称作(A0,p0,X0)的M-纤维式闭映射柱邻域.
证明记收缩映射c:I×I→I×{0}∪∂I×I,进而有按下述方式定义的映射:
c1:BA×I×I→BA×I×{0}∪BA×∂I×I,
c2:BX×I×I→BX×I×{0}∪BX×∂I×I,
ci(b,s,t)=(b,p1r(s,t),p2c(s,t))

也为收缩映射.按M-纤维式映射柱中等价条件作商,易得如下方式定义的M-纤维式收缩映射
(R,r):(Mα×I,pM×id,Mβ×I)→
(Mα×{0}∪(A0BA)×I,
pM×{0}∪(p0pB)×I,Mβ×{0}∪(X0BX)×I),
且满足如下交换

其中pM为按如下商映射交换
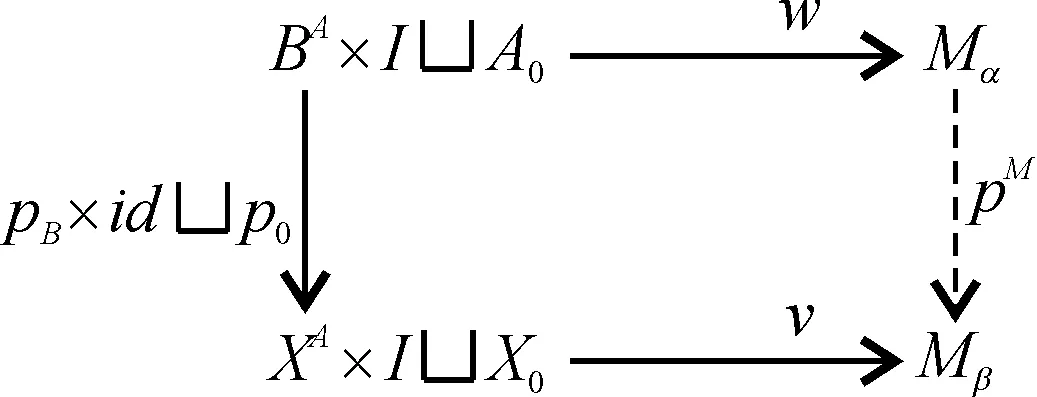
诱导的pB×idp0的下放,(w,v)为粘合M-纤维式映射柱中等价类的M-纤维式商映射.
由定理1可知,(M(α,β),(A0,p0,X0)(BA,pB,BX))具有M-纤维式同伦扩张性质,且根据题设,(,ξ):M(α,β)→(NA,pN,NX)为同胚,|A0=idA0,ξ|X0=idX0易得((NA,pN,NX),(A0,p0,X0)也具有M-纤维式同伦扩张性.如下所示诱导:
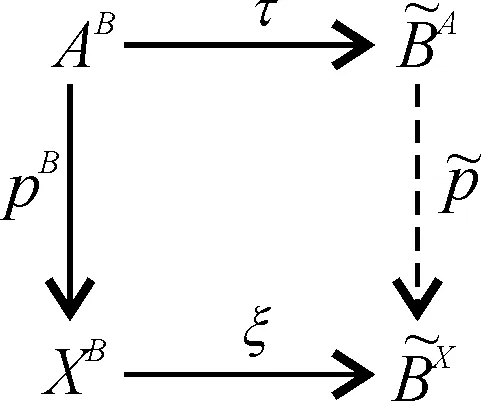
下证((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质.令(g1,g2):(A,p,X)→(E,f,B),(G1,G2):(A0×I,p0×id,X0×I)→(E,f,B),满足:
G1|A0×{0}=g1|A0,G2|X0×{0}=g2|X0.
即存在并满足如下交换:
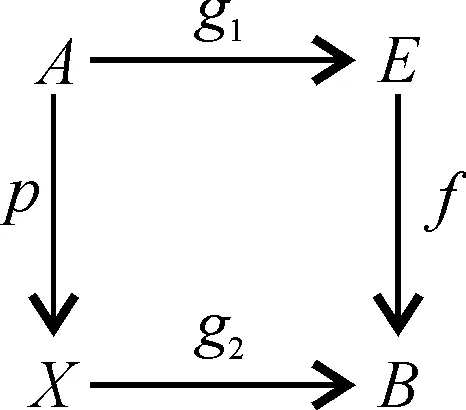
(1)
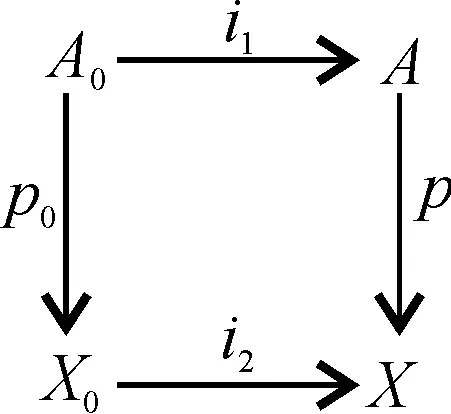
(2)
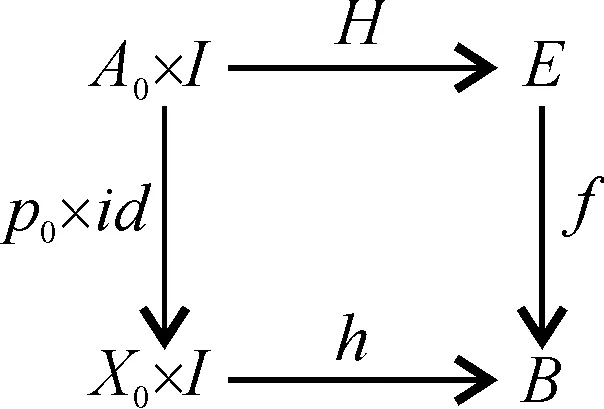
(3)
根据(H,h)定义及交换(1)易得如下交换.
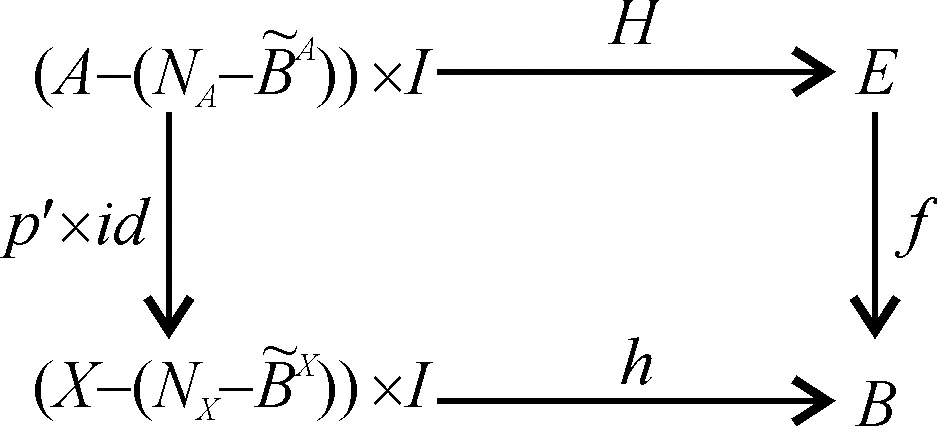
(4)
由((NA,pN,NX),(A0,p0,X0)可M-纤维式同伦扩充,则对于(g1,g2)|(NA,pN,NX):(NA,pN,NX)→(E,f,B)和按如下方式定义的(,):((A0,p0,X0)表示M-纤维式空间(A0,p0,X0)中的元素)
其中
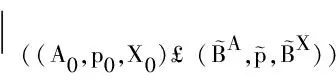


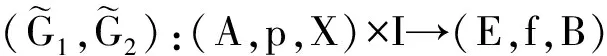


故由定义5知((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质.
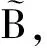
2 M-纤维式同伦扩张性质的应用
上一节讨论了((A,p,X),(A0,p0,X0))的M-纤维式同伦扩张性质成立的等价条件.本节将进一步讨论性质应用.首先,假设(A0,p0,X0)是M-纤维式可缩空间,则有定理2.
定理2的证明由于子空间(A0,p0,X0)是可缩的,则设有同伦

(A,p,X).
由于((A,p,X),(A0,p0,X0))具有同伦扩张性质,故上述映射可扩张成(H,h):(A,p,X)×I→(A,p,X)满足H0=idX,h0=idA而H1(X)与h1(A)为X和A中的单点.
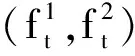
将(A0,p0,X0)映到一点.
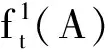
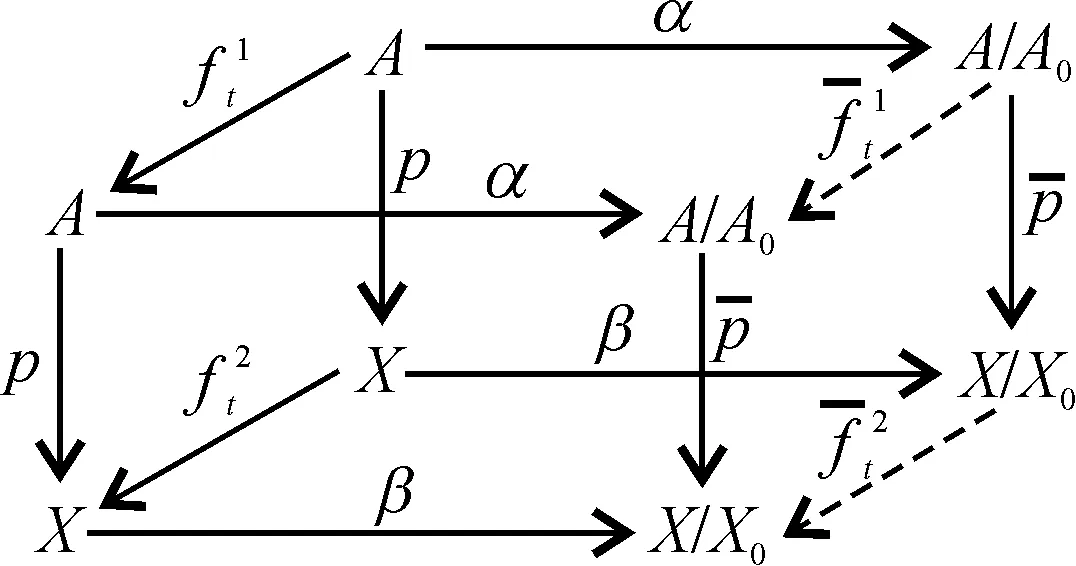
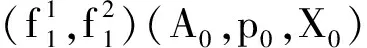

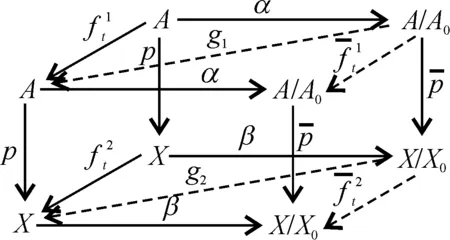
故有
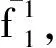
(idA/A0,idX/X0),
故(g1,g2)和(α,β)是互为M-纤维式同伦逆的M-纤维式同伦等价.
推论4[3]若(X,A)具有同伦扩张性质且A可缩,则商映射q:X→X/A是同伦等价.
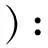
性质3 若((A,p,X),(A0,p0,X0))具有同伦扩张性质且包含映射(i1,i2):(A0,p0,X0)→(A,p,X)是同伦等价,则(A0,p0,X0)是(A,p,X)的形变收缩核.
证明设(r1,r2):(A,p,X)→(A0,p0,X0)是(i1,i2):(A0,p0,X0)→(A,p,X)的同伦等价,即
(r1,r2)(i1,i2)≃M(idA0,idX0),
(i1,i2)(r1,r2)≃M(idA,idX).
下证(r1,r2)与一收缩映射(R1,R2):(A,p,X)→(A0,p0,X0)同伦.
设(H,h):(A0×I,p0×id,X0×I)→(A0,p0,X0)为(r1,r2)(i1,i2)到(idA0,idX0)的同伦,则
(H,h)(,0)=(r1,r2)()(∀(A0,p0,X0).
又根据((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质有(H′,h′):(A×I,p×id,X×I)→(A0,p0,X0),使得:
(H′,h′)(,0)=(r1,r2)() ((A,p,X)),
(H′,h′)|(A0×I,p0×id,X0×I)=(H,h).
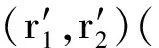
推论5[3]若(X,A)具有同伦扩张性质且包含映射i:A→X是同伦等价,则A是X的形变收缩核.
下面将定义3中的映射设定成从(A0,p0,X0)到(E,f,B)的贴附映射,构造出包含(E,f,B)的贴附空间((E,f,B)(α,β)(A,p,X)),并进一步证明偶对((E,f,B)(α,β)(A,p,X),(E,f,B))具同伦扩张性质.
性质4 若((A,p,X),(A0,p0,X0))具有同伦扩张性质,则对于M-纤维式映射(α,β):(A,p,X)→(E,f,B),其贴附空间与(E,f,B)组成的偶对((E,f,B)(α,β)(A,p,X),(E,f,B))满足同伦扩张性质.
证明由((A,p,X),(A0,p0,X0))具有M-纤维式同伦扩张性质,故可得到收缩映射
(R,r):(A×I,p×id,X×I)→
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I),
进而
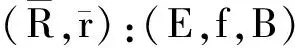
(A×{0}∪A0×I,p∪p0×id,X×{0}∪X0×I)
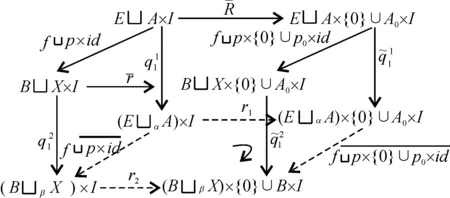
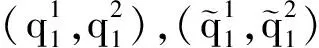
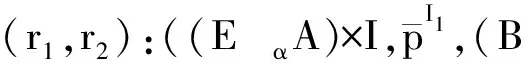
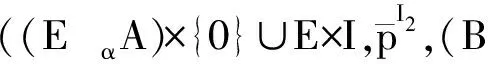
由定理1易见((E,f,B)(α,β)(A,p,X),(E,f,B))具有M-纤维式同伦扩张性质.
推论6[3]若(X,A)具有同伦扩张性质,f:A→Y为连续映射,则贴附空间YfX与Y组成的偶对(YfX,Y)满足同伦扩张性质.
以下假设2个从(A0,p0,X0)到(E,f,B)的贴附映射M-纤维式同伦,证明2个贴附空间关于(A0,p0,X0)相对同伦.下面给出定理3的证明.
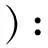
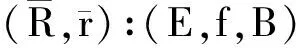
(H,h):((E,f,B) (A×I,p×id,X×I))×I→
(E,f,B) (A×I,p×id,X×I)
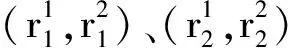

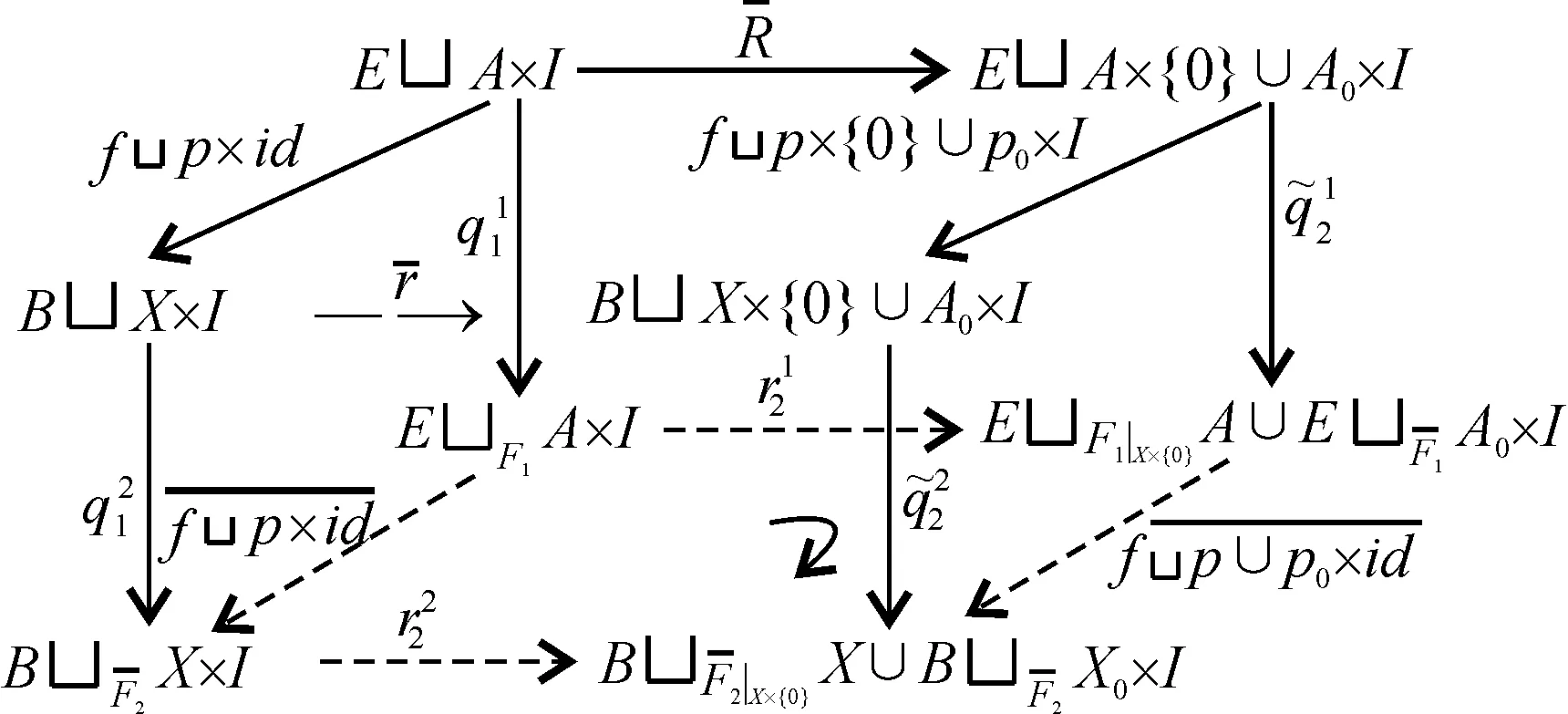
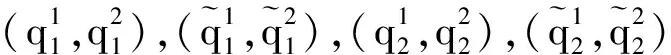
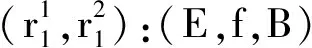
(E,f,B)(f1,f2)(A,p,X),
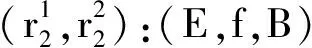
(E,f,B)(g1,g2)(A,p,X).
对应收缩映射r1,r2的形变收缩记作为(H1,h1)和(H2,h2).

(E,f,B)(g1,g2)(A,p,X)≃M(H,h)
(E,f,B)(F1,F2)(A,p,X)rel(A0,p0,X0),
(E,f,B)(f1,f2)(A,p,X)≃M(H,h)
(E,f,B)(F1,F2)(A,p,X)rel(A0,p0,X0).
又由于空间相对同伦等价为等价关系可传递:
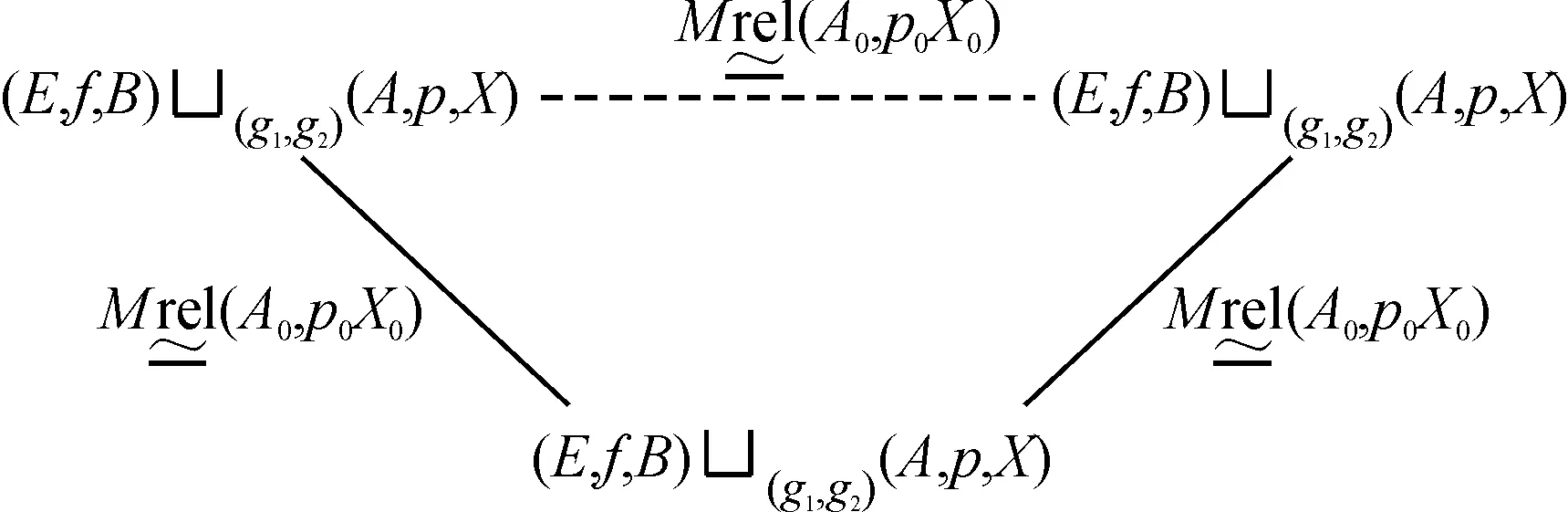
故结论成立.
推论7[3]若(X,A)具有同伦扩张性质,f,g:A→Y是贴附映射且映射f同伦于映射g,则YfX≃YgXrelA.
最后利用M-纤维式同伦扩张性质和上述所得结论给出定理4的证明.
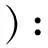
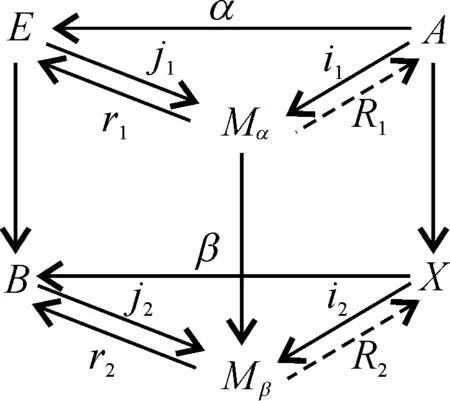
下面说明(α,β)为同伦等价⟺(i1,i2)为同伦等价.
(⟹)若(α,β)为同伦等价,则由(i1,i2)≃M(j1,j2)(α,β)可得(i1,i2)为同伦等价,再根据性质3有(A,p,X)是M-纤维式映射柱M(α,β)的形变收缩核.
(⟸)若(i1,i2)为同伦等价,由(α,β)=(r1,r2)(i1,i2)得f也是同伦等价
故此命题转化为(i1,i2):(A,p,X)→M(α,β)为同伦等价⟺(A,p,X)是M-纤维式映射柱M(α,β)的形变收缩核.下面对此命题展开证明:
(⟸)显然,图中的收缩映射(R1,R2)即为(i1,i2)的同伦逆.
(⟹)因为(A,p,X)在M(α,β)中有一如性质2定义的闭映射柱邻域(A,p,X)×[1/2,1],其中映射f令为id(A,p,X),则M(α,β)即为(A,p,X)×[0,1].构造同胚:
(ω,η)(,t)=(,
满足
(ω,η)|(A,p,X)×{0}=id(A,p,X),
(ω,η)((A,p,X)×{1})=(A,p,X)×{1/2},
(A,p,X)×[0,1/2]-(A,p,X)×{1/2}
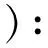
推论8[3]映射f:X→Y为同伦等价当且仅当X是映射柱Mf的形变收缩核.故拓扑空间X与Y同伦等价当且仅当存在一个空间以X及Y为形变收缩核.
参考文献:
[1] Buhagiar D. A category of continuous maps[J]. RIMS Kokyuroku, 1999, 1107: 70-83.
[2] Buhagiar D. The category MAP[C]∥Memoirs of Faculty of Science and Engineering: Series B. Shimane, Matsue: Shimane University,2001, 34: 1-19.
[3] Hatcher A. Algebraic topology[M]. Cambridge: Cambridge Univiversity Press, 2001.
[4] James I M. General topology and homotopy theory[M]. Berlin: Springer-Verlag, 1984.
[5] James I M. Fibrewise topology[M]. Cambridge: Cambridge University Press, 1990.
[6] Hotta T, Miwa T. A new approach to fibrewise fibrations and cofibrations[J]. Topology and Its Applications, 2002, 122(1/2):205-222.
[7] Crabb M, James I M. Fibrewise homotopy theory[M]. London: Springer-Verlag,1998.
[8] 赵浩,沈文淮. M-纤维式纤维化的特征与诱导M-纤维式纤维化[J]. 数学杂志, 2006(3):297-304.
Zhao H, Shen W H. Characterization of M-fibrewise fibration and its induced M-fibrewise fibration[J]. Journal of Mathematics, 2006(3):297-304.
[9] 张亚茹,沈文淮. H-arrow群与CoH-arrow群[J]. 华南师范大学学报:自然科学版, 2006(3): 37-41.
Zhang Y R, Shen W H. H-arrow group and CoH-arrow group[J]. Journal of South China Normal University:Natural Science Edition, 2006(3): 37-41.

