一题三解寻本质 蹊径另辟有巧法——2014江苏省高考物理选择题第5题赏析

(1．江苏省泗洪中学，江苏 泗洪 223900；2．江苏省丹阳市实验学校，江苏 丹阳 212331)

用简洁明了的图像表达具体复杂的物理过程，是自然科学领域研究问题的常用方法.而图像问题也一直是物理高考的热点，数形结合是解决此类问题的主要方法.2014年江苏高考物理第5题以常见的匀变速直线运动模型为研究对象，探究v-x图像.笔者刚接触此题通过求解时发出疑问：如果考生数学功底不深，不了解抛物线的图像特点怎么办？后来通过三种方法的求解，试图揣测命题者的意图，最终得出的结论是：不可否认，根据物理规律结合数学知识可以解答，但是本题更多的是考查匀变速直线运动的基本公式和规律的应用，并非一定要用代数知识才能解答.

原题呈现：一汽车从静止开始做匀加速直线运动，然后刹车做匀减速直线运动，直到停止.下列速度v和位移x的关系图像中，能描述该过程的是( ).

图1

1 数形结合，求解v-x表达式和图像

根据题意，设匀加速的加速度为a1，匀减速速度为a2，最大速度为vm,从静止出发到停止的位移为xm，根据匀变速直线运动的位移速度公式可得：在加速阶段有：v2=2a1x，在减速阶段有：v2=2a2x2，x2=xm-x.

根据以上数学表达式可得：v-x图像应为抛物线，且加速阶段为开口向右，减速阶段开口向左，这样轻松得出答案A.

此方法利用物理规律求解函数表达式，根据函数图像特征得出答案，数学的抛物线知识起到了至关重要的作用.

2 取特殊值列表作图

虽然本题只需定性分析，但是枚举特殊值定量代入计算，也是可取的方法.所以不妨假设以加速度为2m/s2，加速3s,以加速度为-2m/s2减速运行3s.根据匀变速直线运动的速度与时间公式和位移与时间公式，可得v与x关系列表如下：

v/(m·s-1)0246420x/m0149141718

根据列表作出图像如图2，也可得出答案A.

特殊值代入法，只运用了匀变速直线运动的基本公式，然后对数据进行描点作图，简单易操作没有任何的技术含量，对解决选择题有奇效.

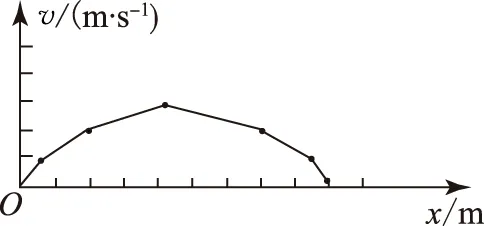
图2

3 从图像的斜率入手

v-x图像的斜率K=Δv/Δx(Δx→0),K值的大小变化决定图像的走势.

因为Δv=a1Δt,从时间间隔的比例关系中不难看出时间间隔不断在减小，因此Δv也在减小，所有加速阶段K值不断的减小.同理可得减速阶段的K值变大有，答案A正确.

(2)控制Δv不变，等效为选取连续相同的时间间隔，初速度为零的匀加速过程通过的位移之比为1∶3∶5∶7∶9∶…

因为Δx逐渐增大，所以加速阶段的K值不断减小.同理可得减速阶段的K值不断变大，答案A正确.

综上所述可得：从解决此题的实效性来看，代数方法简单直接是不可否认的.但是这对学生的数学能力要求很高.利用方法三分析，不难看出本题考查的仍然是匀变速直线运动的基本公式和规律应用，而且更能体现出物理学的思想和方法，所以出题者意图更多的是考查学生对匀变速规律的理解和应用，不需拘泥于运用某种具体的数学方法.