蒸汽发生器多目标优化设计

陈磊，阎昌琪，王建军

(哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001)

提高单堆功率是目前核动力发展的一个重要趋势。单堆功率的提高意味着核动力设备质量和体积随之增加，使得其运输和布置难度加大。另外，在可移动核动力装置中，希望相关设备的结构紧凑、质量轻;同时，一回路流量的增加，主泵输送功率变大，使电厂净电功率输出降低。因此，本文在满足核动力设备运行性能和安全准则的条件下，以SG质量最小、一次侧流量最小为目标，提出一种可用于核动力装置双目标优化设计的新方法。从目前国内对核动力装置优化研究来看，相关学者的工作主要集中在单目标的优化问题上［1］，而实际的设备设计应权衡多方面因素，才能得到最佳方案，本质上来讲是一个多目标设计问题。已有的多目标优化研究，普遍运用加权因子，将多目标问题转化为单目标优化问题［2］。这种方法严重依赖设计者的主观意识，优化结果与加权因子的选取密切相关。所以，有必要在SG的多目标优化设计中，采用一种全新的算法，使SG设计更客观合理。在本文研究中，保持SG换热性能和二次侧运行压力及给水温度不变，耦合堆芯单通道稳态热工水力计算模型，采用多目标遗传算法对SG进行质量和一次侧流量进行双目标优化设计，得到目标函数非支配解前沿面。

1 SG多目标优化问题表达

1.1 多目标优化问题

多目标问题源于许多实际复杂系统的设计、建模和规划问题。几乎每个重要的现实生活中的决策问题都要在考虑不同约束的同时处理若干个目标。多目标优化问题［3］可以表述为

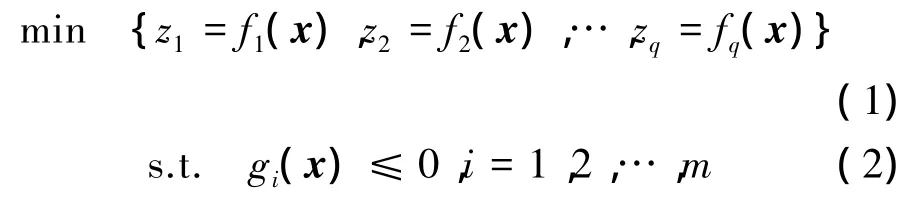
即在满足约束条件下，寻找最优的优化变量x的组合使得目标函数z1，z2，…，zq达到最小。

在实际问题中，目标之间可能无法简单比较，甚至各目标之间相互冲突。例如，在核电厂设计中，设计者既希望电站成本(包括建造、运行和维护)尽量低，又希望电站寿命尽量长。然而，投入成本低的电站往往寿命并不长。因此，存在无法简单比较或冲突的目标(如成本与寿命)时，建立一种不同设计方案的比较机制(设计方案的优劣是通过设计目标进行评定的)，是进行多目标优化的核心。这也使得多目标优化问题与单目标优化问题存在很大区别。

1.2 非支配最优解

在实际问题中，由于存在目标之间无法简单比较，甚至各目标之间相互冲突，不一定存在所有目标上都是最优的解。在有多个目标时，通常存在一系列无法简单进行相互比较的解，这种解称为非支配最优解，其定义［3］如下。

在给定点z0∈Z(Z为多目标函数的解空间)，它是非支配最优解当且仅当不存在其他点z∈Z，使得对于最小化情况有:

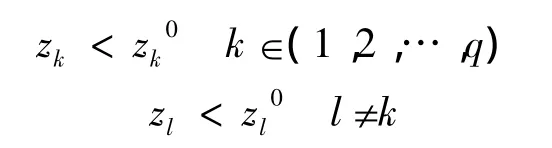
如果对于z0存在其他点z满足上式，则点z0称作判据空间中的支配点。由这些解构成的曲面称为非支配解前沿面。

1.3 设备数学模型及优化变量

本文采用秦慧敏等［1］的立式自然循环蒸汽发生器数学模型对其进行多目标优化;同时，采用秦慧敏等［4］提出的堆芯热工水力计算模型约束多目标优化设计过程。

本文设定反应堆功率Qt，二回路饱和蒸汽压力P2和二回路给水温度Tfw。影响SG质量和一次侧流量的运行参数主要有:一回路运行压力P1，堆芯冷却剂入口温度Tin，堆芯冷却剂出口温度Tout，传热管内冷却剂流速v;结构参数主要有传热管外径d和传热管节径比s。因此优化变量可写为

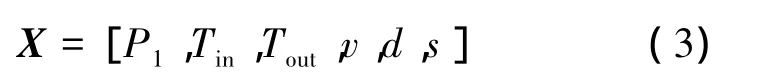
1.4 目标函数

本文以SG质量最小和一次侧流量最小为优化目标。其表达式如下

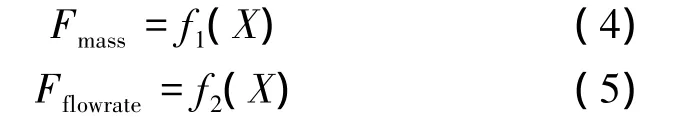
1.5 约束条件

在对SG进行优化设计过程中，本文考虑以下约束:

1)稳态运行时，为确保堆芯安全运行，堆芯最小烧毁比、堆芯热管冷却剂出口温度Thout，燃料芯块中心温度To，包壳表面最高温度Tcs及热管出口含气率xhout，都应限制在一定范围内。

2)稳态运行时，为确保SG在安全壳内正常布置，SG高度必须满足限制要求，且SG传热管束高径比在一定范围内;为保证管板强度，减少管板钻孔数量，SG传热管外径及节距都要确保在一定范围内;为减少SG二次侧腐蚀，二次侧循环速率应大于最低限值;同时，从SG安全和可靠出发，循环倍率也应限制在一定范围内。

3)优化变量具体范围:

2 多目标遗传算法

2.1 改进非支配解排序算法及流程图

Goldberg［3］通过排序法，解决了传统遗传算法在多个目标共存时，适应值分配问题。但是，如何保证计算得到的非支配解的精确度和宽广度，Goldberg并没有提出相应的解决方案。本文结合免疫算法［5］，就如何提高非支配解排序算法所得到的非支配解的精确度和宽广度，提出了一种改进非支配解排序算法。在改进非支配解排序算法中，通过对已得到的非支配解采用免疫克隆和高度变异策略，深度搜索已得到非支配解附近的新解。具体流程图如图1所示。

图1 改进非支配解排序法流程图Fig.1 The flow chart of modified non-dominated sorting genetic algorithm

在本算法中，克隆策略［6］是对已得到的非支配解个体A(it)={a1(it)，…，aN(it)(it)}进行一定数目的复制操作，得到克隆群体A＇(it):

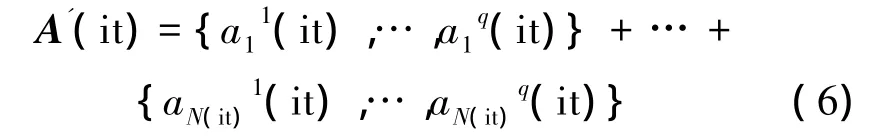
式中:(it)=ai(it)(j=1，…，q)，q为克隆比例。本文采用Michalewicz提出的变异策略［6］，在进化初期，变异个体有较大的变异范围，以利于全局搜索，改善解的全局性;而在进化后期，个体变异范围较小，以利于局部搜索，加快解的收敛速度。

设个体 s=［v1，v2，…，vn］的分量vk被选择进行变异，其定义域是［ak，bk］，则变异后的个体可表示为

式中:vk＇=vk+Δ(it，bk-vk)，ρ=0=vk-Δ(it，vkak)，ρ=1。其中，ρ取0和1的随机数，it是当前演化代数，函数Δ(it，y)的具体表达式为

式中:r为［0，1］上的随机数;T为最大进化次数;λ是决定非一致程度的参数，其取值范围一般为2～5。

2.2 约束的处理

本文采用排序的方法处理不满足约束条件的解。对于满足约束条件的个体，确定非支配解，使其共享同一适应值，并从余下的个体中确定第2批非支配解，持续该过程，直至对所有满足约束条件的个体分配适应值;对于不满足约束条件的个体，依据违反约束个数由少到多进行排序，并由大到小分配适应值;且最大适应值低于满足约束个体的最小适应值。

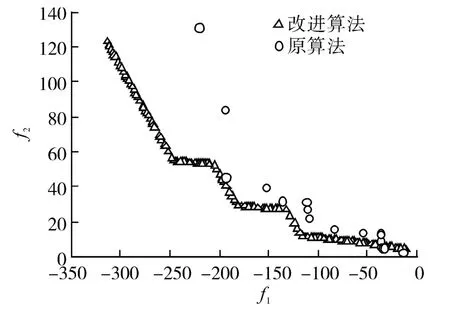
图2 改进非支配解排序算法与原算法优化结果对比Fig.2 The comparison between the modified non-dominated sorting genetic algorithm and its prototype

2.3 算法测试

Osyczka等为多目标算法提出了一种测试函数［3］。本文采用改进非支配解排序算法，最大遗传代数设为300，种群个数设为100，对该测试函数进行寻优，并与原算法进行对比，对比结果如图2所示。由图2可知，改进非支配解算法寻优精度更高、非支配解分布范围更广且分布更连续。

3 敏感性分析

利用所建立的评价程序，分别考察优化变量(p，Tin，Tout，v，dSG，s)偏离母型设计值对SG质量和一次侧流量的影响情况。在分析过程中，保持SG负荷、二次侧压力和给水入口温度不变，6个变量对目标函数响应如图3所示，其中质量、一次侧流量均进行了归一化处理。

由图3可知:1)管内冷却剂流速、传热管径、传热管节径比对SG一次侧流量没有影响。这是因为设计中保持堆芯功率为定值，确定冷却剂进、出口温度，即可确定堆芯流量，单个环路冷却剂流量随之而定。2)压力、堆芯冷却剂出口温度对SG质量及一次侧流量的影响趋势是一致的。压力增加，设备壁厚随之增加，水的比热减小，因此SG质量和一次侧流量增加。提高反应堆出口温度，可提高SG传热温差，减小SG传热面积，减轻SG质量;同时，高的冷却剂出口温度也使反应堆冷却剂进出口温差加大，在反应堆功率不变条件下导致堆芯流量降低。3)提高反应堆进口温度，也能使SG换热温差加大，但是，其使反应堆出口和进口温差减小，堆芯流量随之增加。据此可知，反应堆进口温度的变化必然引起非支配最优解的变化。

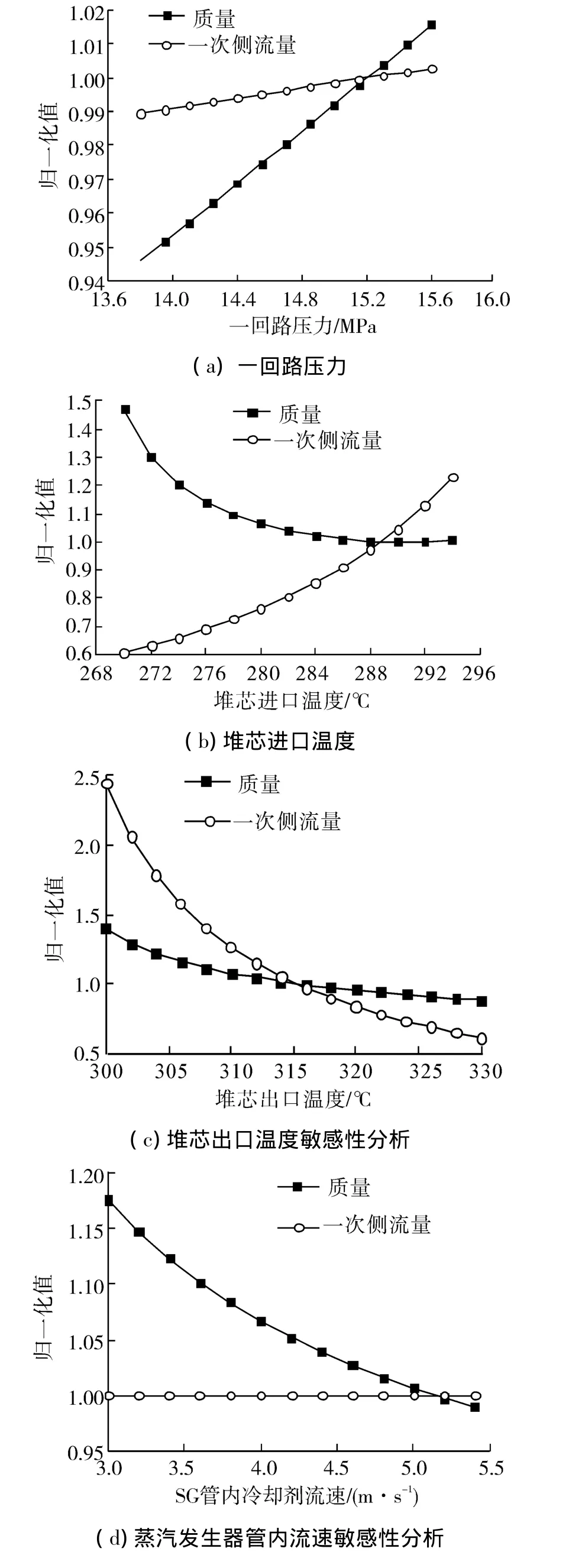
图3 优化变量敏感性分析Fig.3 The sensitivity analyses of the optimization variables

4 优化结果

采用本文所提出的改进非支配解排序算法，以蒸汽发生器质量和一次侧流量为目标，对蒸汽发生器进行多目标优化设计，优化结果如图4。在图4(a)中，给出了目标函数非支配解前沿面。SG质量最大可减小17.66%，一次侧流量最大可减少17.58%。图4(b)～(e)给出了所得到非支配解中，优化参数随蒸汽发生器质量的变化趋势。

由图4可以看出:1)在以质量和一次侧流量为目标的蒸汽发生器双目标优化设计中，所得到的非支配解和相应的优化变量分为两个连续区域。由4(a)可知，当蒸汽发生器质量优化达到190 t左右时，继续增大蒸汽发生器质量并不能有效减小蒸汽发生器一次侧流量;但当蒸汽发生器质量优化达到225 t左右时，继续增大蒸汽发生器质量能达到减小一次侧流量的目的。2)在所得到的非支配解中，由于冷却剂流量逐渐减小，传热管根数相应减少。在保证传热面积的条件下，需不断增加传热管长度，从而使得蒸汽发生器高度逐渐接近约束上限。在蒸汽发生器质量达到190 t时，蒸汽发生器高度已达到上限，蒸汽发生器一次侧流量的降低，不能再依靠缩减反应堆冷却剂进、出口的温差(图4(c))，而需通过降低冷却剂的流速(图4(d))。由于流量降低的机制发生了改变，使得非支配解中出现了非连续区域。3)由图4(b)～(e)中可知，反应堆进、出口温度严重影响非支配解的分布，这与敏感性分析结果是一致的，而压力、管径和节径比在非支配解2个连续区域内，基本保持定值。蒸汽发生器传热管内流速在第1段连续非支配解集内，其值保持不变;在第2段连续非支配解集内，其值逐渐降低。

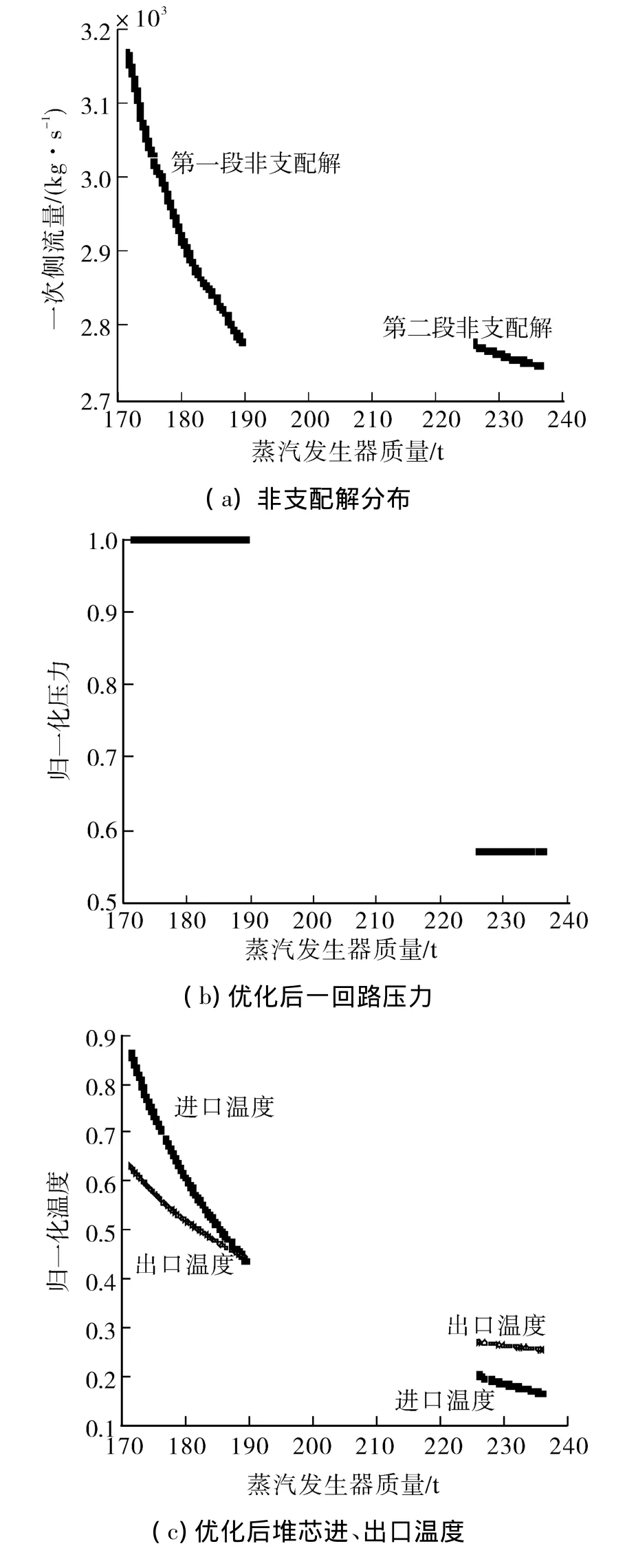
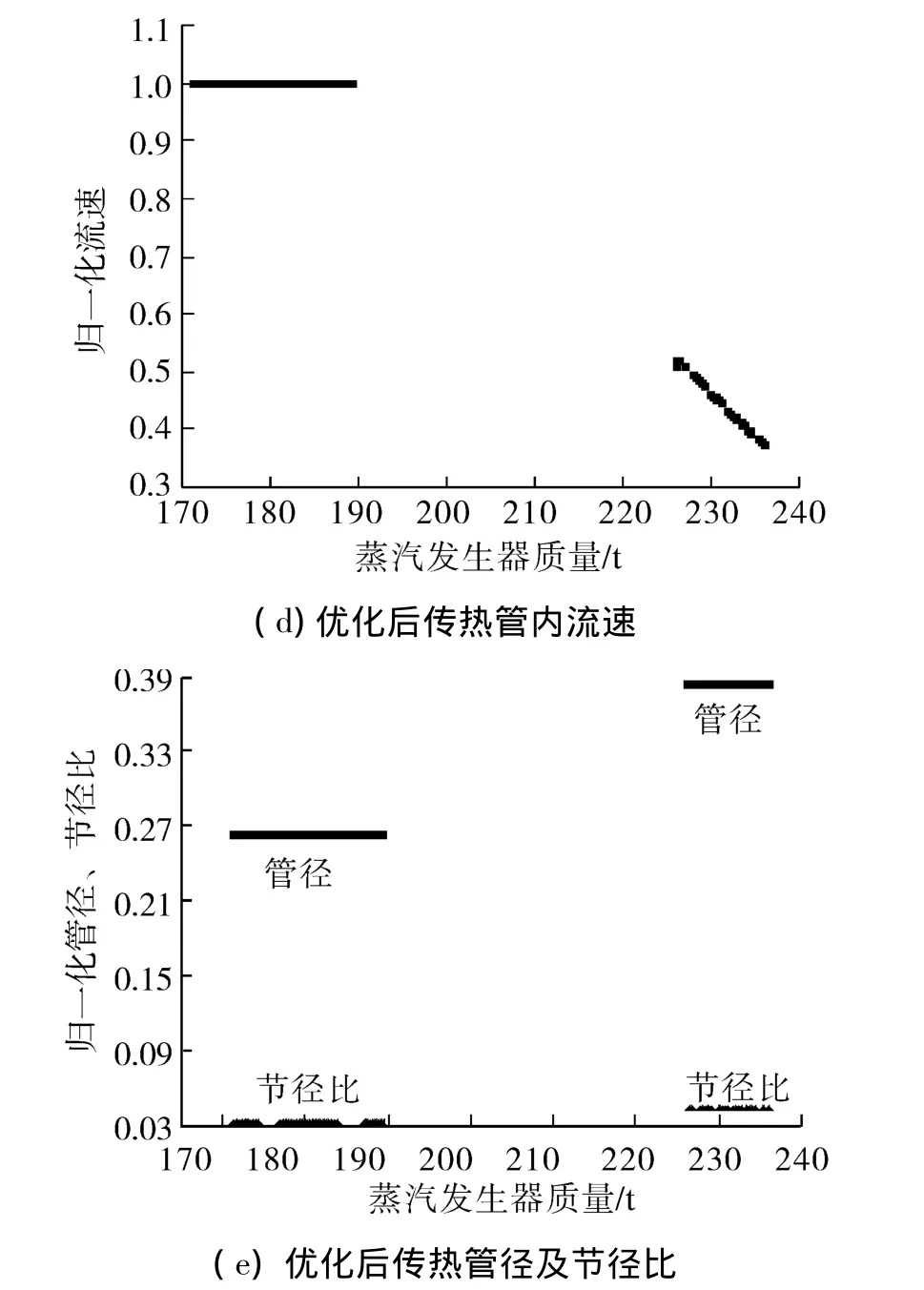
图4 蒸汽发生器多目标优化结果Fig.4 The multi-goal optimization results of the steam generator

在第一段非支配解连续区域内，影响非支配解分布的变量是反应堆进、出口温度。由前文敏感性分析可知:降低反应堆进口温度能够使蒸汽发生器质量增加、一次侧流量降低;降低反应堆出口温度能够使蒸汽发生器质量增加、一次侧流量增加。而由图4(a)非支配解分布可知，蒸汽发生器质量和一次侧流量是一对矛盾的优化目标。所以，反应堆入口温度决定第一段非支配解的分布。

由图3(b)可知，当反应堆入口温度较高时，降低反应堆进口温度对蒸汽发生器质量影响较小，而能显著降低蒸汽发生器一次侧流量;当继续降低反应堆入口温度时，进口温度的降低能明显增大蒸汽发生器质量。所以，在图4(a)第一段连续非支配解中，斜率绝对值逐渐降低。

在第2段连续非支配解中，反应堆进口温度降低速率逐渐变缓，反应堆出口温度基本维持不变，蒸汽发生器进、出口温差增大，蒸汽发生器一次侧流量降低，蒸汽发生器质量增加。在本文研究设计中，堆芯功率保持不变，在反应堆进、出口平均温度降低时，必须通过增加传热面积以导出堆芯热量。此时，传热管径增加(图4(e))，同时，传热管数增加，由于堆芯流量降低，传热管开口面积增大，管内流速降低(图4(d))。

5 结论

本文对蒸汽发生器质量和一次侧流量受优化参数的影响进行了敏感性分析，并应用改进非支配解排序多目标遗传算法对其进行了优化设计，并得出以下结论:

1)与文献［2］所采用的“权重法”相比，本文所引入的“非支配解”概念，为核动力系统多目标优化设计提供了一种新方法;该方法排除了设计人员主观偏好对最优解的影响;另外，能够给出更多的优化方案，供设计参考。

2)采用高频变异策略，增强现有非支配解排序算法局部寻优能力，提高了所得到非支配解的收敛性和连续性。

3)在以质量和一次侧流量为目标的SG双目标优化中，SG质量最大可减轻17.66%;SG一次侧流量最大可减少17.58%。

4)为实现SG优化设计方案投入制造生产，需研究优化方案在设计基准事故下的响应行为。在后期研究中，可采用RELAP5软件搭建SG及其相连一回路模型，研究其瞬态特性。

［1］秦慧敏，阎昌琪，王建军，等.立式自然循环蒸汽发生器的重量优化设计［J］.原子能科学技术，2011，45(1):66-72.QIN Huimin，YAN Changqi，WANG Jianjun，et al.Optimal design of vertical circulation steam generator weight［J］.Atomic Energy Science and Technology，2011，45(1):66-72.

［2］陈林根，胡德明，张俊迈.舰船汽轮齿轮机组一体化初步设计多目标优化［J］.中国造船，1991，44(2):66-71.CHEN Lingen，HU Deming，ZHANG Junmai.Multi-objective optimization of marine steam turbine geared unit in preliminary design［J］.Ship Building of China，1991，44(2):66-71.

［3］玄光男，程润伟.遗传算法与工程优化［M］.于歆杰，周根贵，译.北京:清华大学出版社，2005:76-108.GEN Mitsuo，CHENG Ruiwei.Genetic algorithms and engineering optimization［M］.YU Xinjie，ZHOU Gengui.Beijing:Tsinghua University Press，2005:76-108.

［4］秦慧敏.反应堆一回路系统参数优化研究［D］.哈尔滨:哈尔滨工程大学，2011:11-25.QIN Huimin.Optimization study of parameters for nuclear reactor primary system［D］.Harbin:Harbin Engineering U-niversity，2011:11-25.

［5］焦李成，杜海峰，刘芳，等.免疫优化计算、学习与识别［M］.北京:科学技术出版社，2006:92-93.JIAO Licheng，DU Haifeng，LIU Fang，et al.The immune optimization algorithm，the learning and recognition［M］.Beijing:Science Press，2006:92-93.

［6］焦李成，尚荣华，马文萍，等.多目标优化免疫算法、理论和应用［M］.北京:科学技术出版社，2010:72.JIAO Licheng，SHANG Ronghua，MA Wenping，et al.Theory and application of multi-objective immune algorithm［M］.Beijng:Science Press，2010:72.